FI.ME.013-01 – Física – Mecânica. Equilíbrio estático de corpo rígido.
Ponto material
Um corpo rígido, de dimensões reduzidas em face do referencial, pode ter seu equilíbrio estudado como se fosse um ponto material.
Condição de equilíbrio
Um ponto material está em equilíbrio se a resultante do sistema de forças for nula.
Equilíbrio estático: um corpo está em equilíbrio estático se está em repouso.
Equilíbrio dinâmico: O corpo em equilíbrio dinâmico está em MRU, movimento retilíneo e uniforme. Para isso a resultante das forças que atuam sobre ele também precisa ser nula.
$$\color{NavyBlue}{F_{R} = 0}$$
Vejamos o caso mais simples. Um corpo suspenso por um par de cabos fixos em dois pontos separados por uma distância entre si. Usaremos o processo de decomposição em suas componentes ortogonais das forças de tração suportadas pelos cabos. Analisemos a figura.
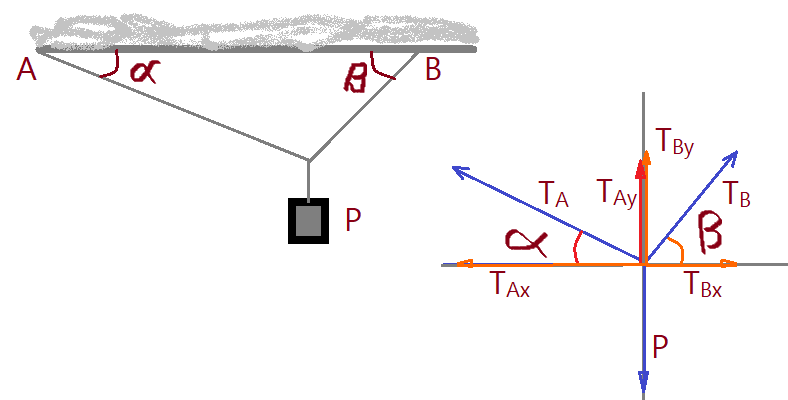
Podemos identificar os cabos A e B, que convergem num ponto, onde se encontram com a vertical que passa pelo Centro de Gravidade do corpo suspenso.
Transpondo as forças de tração $T_{A}$ e $T_{B}$, além do peso $P$, do corpo. Aplicando a decomposição das forças oblíquas em suas componentes horizontal e vertical, obtemos as forças horizontais $T_{Ax}$ e $T_{Bx}$, além das componentes verticais $T_{Ay}$, $T_{By}$ e $P$.
Podemos agora aplicar a determinação da resultante horizontal e vertical. Para haver equilíbrio essas resultantes devem ser nulas.
$\color{Navy}{T_{Ax} – T_{Bx} = 0}$$\Leftrightarrow$$\color{Navy}{T_{Ax} = T_{Bx}}$
$\color{Navy}{T_{Ay} + T_{By} – P = 0}$$\Leftrightarrow$$\color{Navy}{T_{Ay} +T_{By} = P}$
Exemplo 1. – Vamos resolver o problema que segue. Um corpo de $P = 400,0\,N$, está suspenso por uma corda que exerce as trações $T_{A}$ e $T_{B}$, formando ângulos de $30^0$ e $60^0$ respectivamente. Queremos determinar a intensidade dessas trações.
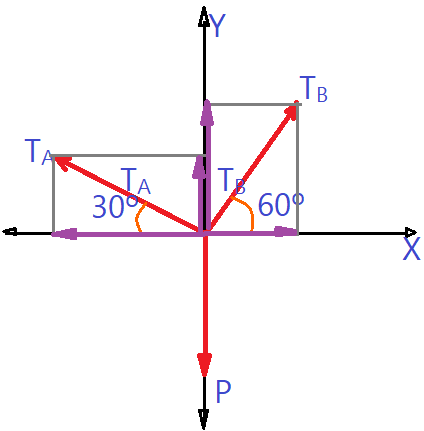
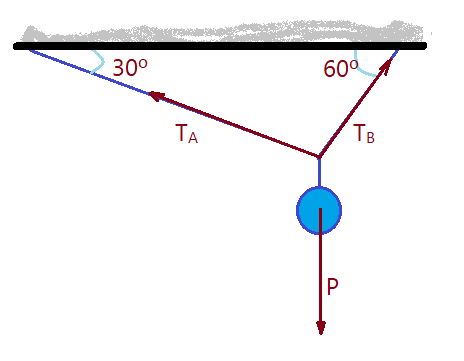
No diagrama de forças vemos as componentes no eixo $X$, que são:
$T_{Ax}= T_{A}\cos {30^0} = \frac{\sqrt{3}}{2}T_{A}$
$T_{Bx}= T_{B}\cos {60^0} = \frac{1}{2}T_{B}$
No eixo $Y$ temos as componentes:
$T_{Ay}= T_{A}sen {30^0} = \frac{1}{2}T_{A}$
$T_{By}= T_{B}sen {60^0} = \frac{\sqrt{3}}{2}T_{B}$
$P = 400\,N$
Vimos que a condição de equilíbrio é ser a resultante nula. Isso implica que as componentes ortogonais também serão nulas.
$F_{Rx} = 0$$\Leftrightarrow$$T_{Bx} – T_{Ax} = 0$
$T_{Bx} = T_{Ax}$$\Leftrightarrow$$\frac{1}{2}T_{B} = \frac{\sqrt{3}}{2}T_{A}$
$T_{B} = \frac{\sqrt{3}}{\not{2}}T_{A}\times \not{2}$$\Leftrightarrow$$ T_{B} = \sqrt{3}T_{A}$
No eixo $Y$ vamos encontrar:
$F_{Ry}= T_{Ay} + T_{By} – P = 0$
$\frac{\sqrt{3}}{2}T_{A} + \frac{1}{2}T_{By} – 400 = 0$$\Leftrightarrow$$\frac{\sqrt{3}}{2}T_{A} + \frac{1}{2}T_{By} = 400$
Substituindo a primeira na segunda equação, obtemos:
$\frac{\sqrt{3}}{2}T_{A} + \frac{1}{2}\times \sqrt{3}T_{A} = 400$$\Leftrightarrow$$\frac{\sqrt{3}}{2}T_{A} + \frac{3}{2}T_{A} = 400$
${\not{2}}\times \sqrt{3}{\not{2}}T_{A} = 400$$\Leftrightarrow$$\sqrt{3}T_{A} = 400$
$T_{A} = \frac{400}{\sqrt{3}} = \frac{400\times\sqrt{3}}{\sqrt{3}^2}$
$$\color{Sepia}{T_{A}= \frac{400\sqrt{3}}{3}\,N}$$
$T_{B}= \sqrt{3}\times T_{A} = \sqrt{3}\frac{400\sqrt{3}}{3}$$\Leftrightarrow$$T_{B}=\frac{\sqrt{3}^2\times 400}{3}$
$T_{B} = \frac{\not{3}\times 400}{\not{3}}$$\Leftrightarrow$$T_{B} = 400\,N$
$$\color{Navy}{T_{B}= 400\,N}$$
Exemplo 02. – Vejamos o sistema da figura que segue. Determine as forças de tração suportadas pelas cordas A e B, para sustentar o peso do corpo que é de $P = 500,0\,N$.
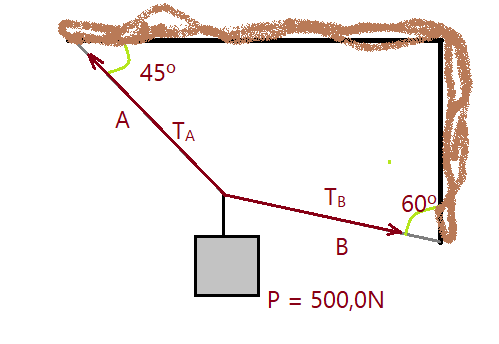
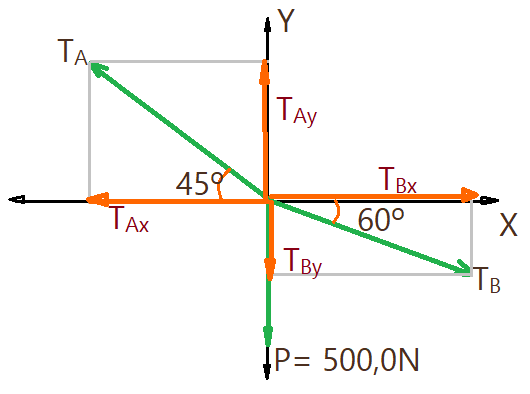
Vamos aplicar a condição de equilíbrio na determinação das trações pedidas.
Observando o diagrama de forças, vemos que há duas componentes no eixo $X$ e três componentes no eixo $Y$.
$$\color{Brown}{F_{Rx} = T_{Bx} – T_{Ax} = 0}$$
$T_{Ax} = T_{A}cos {45^0}$$\Leftrightarrow$$ T_{Ax} = T_{A}\times \frac{\sqrt{2}}{2}$
$T_{Bx} = T_{B}cos {30^0}$$\Leftrightarrow$$T_{Bx} = T_{B}\times\frac{\sqrt{3}}{2}$
Substituindo na expressão acima:
$F_{Rx} = \frac{\sqrt{2}}{2}T_{A} – \frac{\sqrt{3}}{2}T_{B} = 0$
$\frac{\sqrt{2}}{2}T_{A} = \frac{\sqrt{3}}{2}T_{B}$
$T_{A} = \frac{\sqrt{3}}{2}T_{B}\times \frac{2}{\sqrt{2}}$
$T_{A} = \frac{\sqrt{3}}{\not{2}}\times\frac{\not{2}}{\sqrt{2}}T_{B}$
$T_{A} = \frac{\sqrt{3}}{\sqrt{2}}\times T_{B}$$\Leftrightarrow$$T_{A} = \frac{\sqrt{3}\times \sqrt{2}}{\sqrt{2}^2}T_{B}$
$$\color{Sepia}{T_{A} = \frac{\sqrt{6}}{2} T_{B}}$$ (I)
No eixo $Y$, teremos:
$T_{Ay} = T_{A}sen {45^0} = T_{A}\frac{\sqrt{2}}{2}$
$T_{By} = T_{B}sen {30^0} = T_{B}\frac{1}{2}$
Não se pode deixar de observar que a componente da tração $T_{B}$ no eixo $Y$ é dirigida para baixo. Assim teremos:
$F_{Ry}= T_{Ay} – T_{By} – P = 0$$\Leftrightarrow$$T_{A}\frac{\sqrt{2}}{2} – T_{B}\frac{1}{2} = 500,0$
$\frac{\sqrt{6}}{2} T_{B}\frac{\sqrt{2}}{2} – T_{B}\frac{1}{2} – 500,0 = 0$
$\frac{\sqrt{6\times 2}}{4}T_{B} – T_{B}\frac{1}{2} = 500,0$$\Leftrightarrow$$\frac{\sqrt{3\times 4}}{4}T_{B} – \frac{1}{2}T_{B} = 500,0$$
$\frac{2\sqrt{3}}{4}T_{B} \frac{1}{2}T_{B} = 500,0$$\Leftrightarrow$$\frac{\sqrt{3}}{2}T_{B} – \frac{T_{B}}{2} = 500,0$
$\frac{\sqrt{3} – 1}{2}T_{B} = 500,0$$\Leftrightarrow$$T_{B} = \frac{1000,0}{\sqrt{3} – 1}$
$T_{B} = \frac{1000\times{\sqrt{3} + 1}}{{\sqrt{3}- 1}\times{sqrt{3} +1}}$
$T_{B}= \frac{1000\times{\sqrt{3} + 1}}{\sqrt{3}^2 – 1}$$\Leftrightarrow$$T_{B}=\frac{1000\times{\sqrt{3} + 1}}{2}$
$$\color{Navy}{T_{B} = 500\times{\sqrt{3} + 1}}= 500\times {2,732}= 1366\,N$$
$T_{A} = \frac{\sqrt{6}}{2} T_{B}$
$T_{A} = \frac{\sqrt{6}}{2}\times {1366}$$\Leftrightarrow$$T_{A}= {2,449}\times{683} = 1673\,N$
$$\color{Navy}{T_{A}\simeq 1673\,N}$$
03. Aplique a condição de equilíbrio e determine as trações nas cordas que sustentam os corpos nas duas figuras abaixo considerando a aceleração da gravidade igual a $g= 10\,m/s^2. Denomine as figuras de 3.1 e 3.2
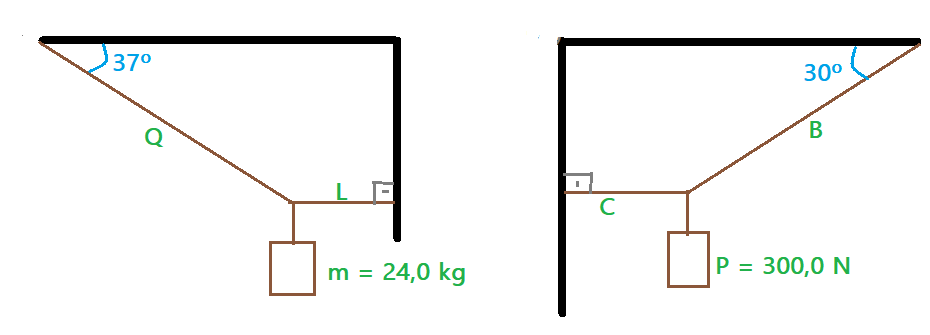
Respostas: 3.l. $T_{Q}=400\, N$ e $T_{L} = 320\,N$
3.2 $T_{B}= 600\,N$ e $T_{C} = 300\sqrt{3}\,N$
04. Determine as forças de tração suportadas pelos cabos que sustentam os corpos suspensos por elas nas ilustrações das figuras abaixo.
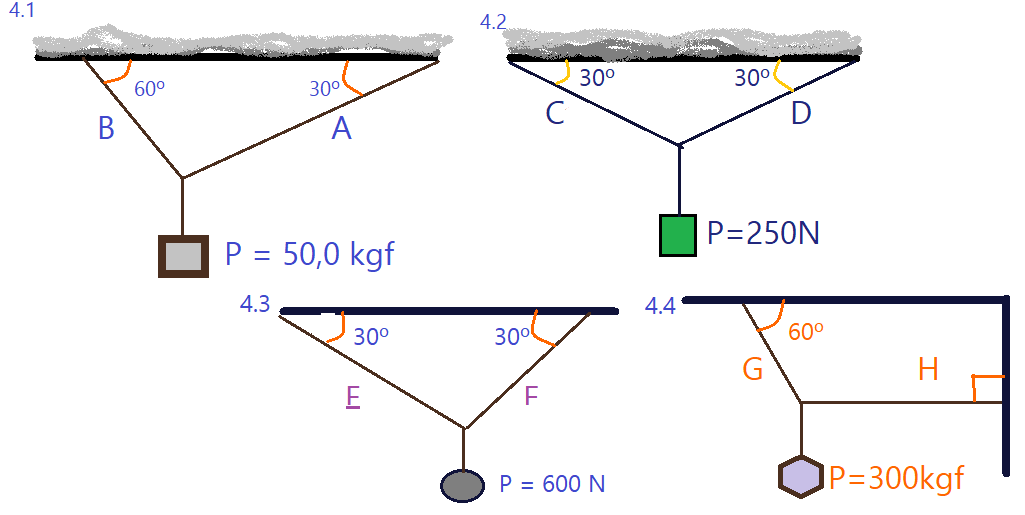
05. Determine a força de tração na corda que sustenta a esfera e a reação da parece em que ela está encostada, nas figuras abaixo.
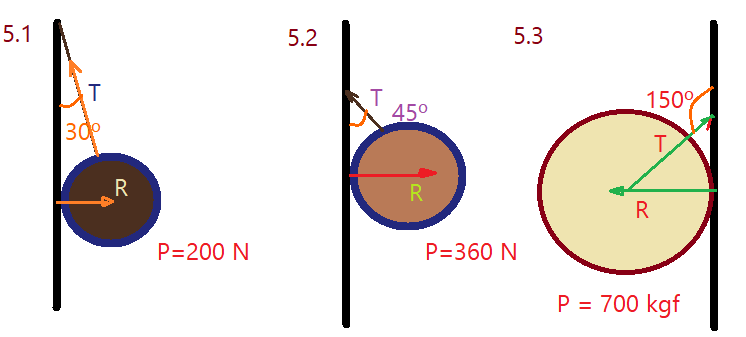
Equilíbrio de rotação: se o corpo tiver dimensões que não permitem considerar sua massa concentrada em um ponto, torna-se necessário aplicar o Teorema do Momento Estático Resultante ou Torque que também precisa ser nulo. Isso tem aplicação no caso de vigas, escoras, apoios em diferentes pontos, cargas sobre estruturas.
Teorema de Varignon
Em um sistema com várias forças atuando sobre um mesmo corpo, em posições diferentes, o Momento Estático da resultante em relação de determinado ponto, é igual à somatória dos momentos das componentes em relação ao mesmo ponto.
$$\color{Navy}{M_{o}R = M_{o}F_1 + M_{o}F_2 + … + M_{o}F_n}$$
$$\color{NavyBlue}{M_{o}R = \sum_1^n(M_{0}F_n)}$$
Para existir o equilíbrio de rotação, temos então duas condições.
$$\color{NavyBlue}{F_{R} = 0}$$
$$\color{NavyBlue}{M_{o}R= 0}$$
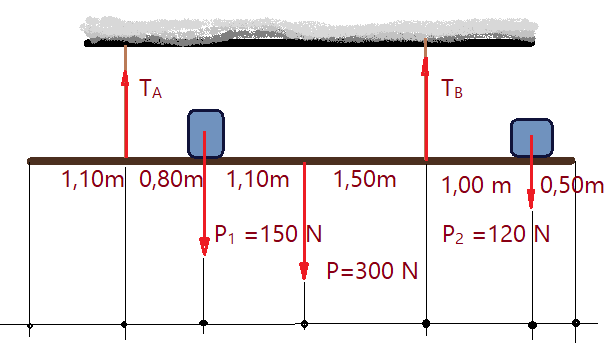
Exemplo 3. – Seja uma barra rígida de comprimento $L$, peso $P$, disposta horizontalmente, recebe a ação de forças verticais e inclinadas como mostra a figura. Vamos determinar as intensidades das forças de tração exercidas pelos cabos sobre a barra.
Vamos começar pela primeira condição de equilíbrio. Força resultante igual a $0$ (zero).
$$\color{NavyBlue}{F_{X} = 0}$$
$F_{R} = T_{A} + T_{B} – P_{1} – P_{2} – P = 0$
$T_{A} + T_{B} = 300 + 150 + 120$$\Leftrightarrow$$\color{Sepia}{T_{A} + T_{B} = 570}$ (I)
Temos a soma das duas incógnitas. Aplicamos agora a segunda condição de equilíbrio. Temos que escolher um ponto como centro de rotação, que pode ser tomado livremente. Escolheremos para este caso a extremidade da esquerda. Os braços serão obtidos somando as distâncias entre as forças.
$$\color{NavyBlue}{M_{o}R= 0}$$
$0 = T_{A}\times {1,10} + P_{1}\times {-1,90} + P\times{- 3,0} + T_{B}\times {4,5} + P_{2}\times {5,50}$
$0 = T_{A}\times{1,10} + T_{B}\times {4,5} – {1,90}\times {150} – {3,0}\times {300} – {5,5}\times {120}$
$T_{A}\times{1,10} + T_{B}\times{4,5} = 285 + 900 + 660$
$T_{A}\times{1,10} + T_{B}\times{4,5} = 1845$ (II)
Da equação (I), podemos isolar uma das forças de tração e substituir na (II)
$T_{A} + T_{B} = 570$$\Leftrightarrow$$T_{A} = 570 – T_{B}$
${1,10}\times{570 – T_{B}} + T_{B}\times{4,5} = 1845$
$637 – {1,10}T_{B} + {4,50}T_{B} = 1845$$\Leftrightarrow$$3,40 T_{B} = 1845 – 637$
$T_{B} = \frac{1208}{3,40}$$\Leftrightarrow$$\color{NavyBlue}{T_{B} = 355,29N}$
$T_{A} = 570 – T_{B}$$\Leftrightarrow$$\color{NavyBlue}{T_{A} = 570 – 355,29 = 214,71N}$
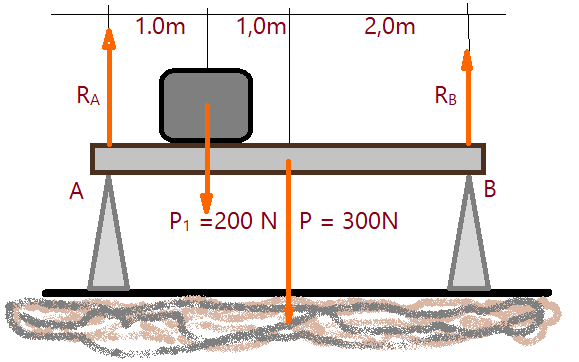
Exemplo 4. – Uma barra rígida, tem $4,0\,m$ de comprimento e peso $P=300,0\,N$. Sobre ela, no ponto médio de sua metade esquerda, apoia-se um bloco de peso $P_{1}=200,0\,N$. As extremidades estão apoiadas sobre dois cutelos A e B que sustentam a estrutura. Determinar a intensidade das forças de reação nos apoios A e B.
Começaremos pela condição de equilíbrio estático, isto é, a força resultante é nula.
$F_{R} = 0$$\Leftrightarrow$$ R_{A} + R_{B} – P_{1} – P = 0$
$R_{A} + R_{B} = 200,0 + 300,0$$\Leftrightarrow$$R_{A} + R_{B} = 500,0\,N$
Consideremos o eixo de rotação em torno do ponto de apoio A. Vejamos agora a aplicação do equilíbrio de rotação que é Momento Resultante.
$\sum_1^n = 0$$\Leftrightarrow$$M_{o}R_{A} + M_{o}R_{B} + M_{o}P_{1} + M_{o}P = 0$
$R_{A}\times 0 + R_{B}\times 4 – {200,0}\times {1,0} – {300,0}\times 2 = 0$
$ 0 +4R_{B} = 200 + 600$$\Leftrightarrow$$ R_{B} = \frac{800}{4}$
$$\color{Navy}{R_{B} = 200,0\,N}$$
$R_{A} + R_{B} = 500,0$$\Leftrightarrow$$R_{A} + 200,0 = 500,0$
$$\color{Navy}{R_{A} = 500,0 – 200,0 = 300,0\,N}$$
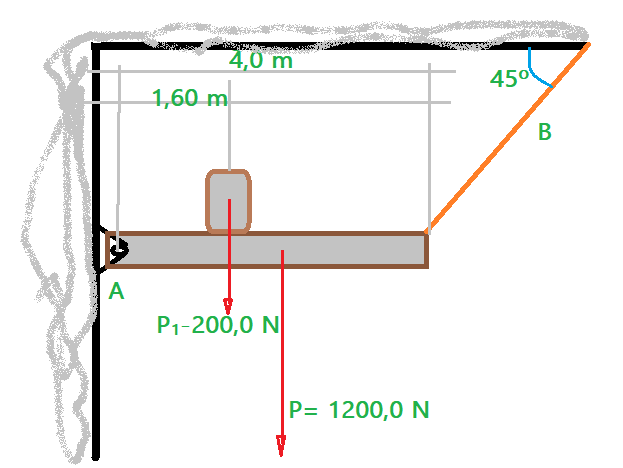
Exemplo 5. Na figura está representada uma barra horizontal, de $P= 1200,0\,N$, articulada em um suporte na extremidade A e tendo apoiado sobre ela um bloco de $P_{1}=200,0\,N$, à distância de $1,6\,m$ da articulação. Na outra extremidade um cabo B sustenta a barra na posição horizontal, formando um ângulo de $\theta = 45^0$. Determinar a intensidade da força de tração no cabo B e a intensidade das reações horizontal e vertical do pino da articulação.
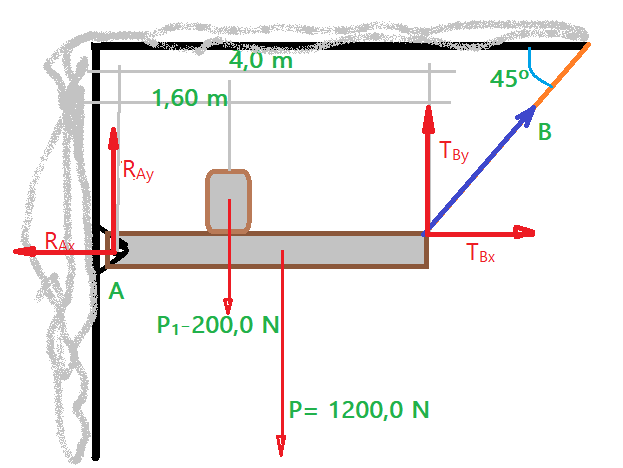
Na figura ao lado estão representadas, além da barra articulada, as forças e suas componentes. Note que há duas componentes horizontais que são $T_{Bx}$ e $R_{Ax}$. As demais são verticais como $T_{By}$, $R_{Ay}$, $P_{1}$ e $P$. Para obter as respostas pedidas no enunciado, iriemos aplicar as condições de equilíbrio estático, dinâmico e rotacional.
Na horizontal temos:
$R_{X} = 0$$\Leftrightarrow$$ T_{BX} – R_{Ax} = 0$
$R_{AX} = T_{Bx}$$\Leftrightarrow$$ R_{Ax} = T_{B}\times cos {45^0}$
$$\color{Maroon}{R_{Ax}= T_{B}\frac{\sqrt{2}}{2}}$$ (I)
Na vertical encontramos:
$R_{X} = 0$$\Leftrightarrow$$ R_{Ay} + T_{By} – P_{1} – P =0$
$R_{Ay} + T_{B}\frac{\sqrt{2}}{2} = 200,0 + 1200,0$
Substituindo (I) nesse equação, teremos:
$R_{Ay} + R_{Ax} = 1400,0$ (II)
No equilíbrio rotacional, tomamos a articulação em A como eixo de rotação.
$\sum_1^n = 0$$\Leftrightarrow$$0 = R{Ax}\times {0} + R_{Ay}\times {0} – P_{1}\times {1,6} – P\times {2,0} + T_{BY}\times {4,0} + T_{Bx}\times {0} $
$0 = 0 + 0 – 320,0 – 2400,0 +T_{By} + 0$$\Leftrightarrow$$4T_{By} = 2720,0$
$T_{By}= \frac{2720,0}{4}$$\Leftrightarrow$$\color{Maroon}{T_{By} = 680,0\,N}$
$T_{By} = T_{B}\frac{\sqrt{2}}{2}$$\Leftrightarrow$$ T_{B} = \frac{2T_{By}}{\sqrt{2}}$
$T_{B} = \frac{2T_{By}\times \sqrt{2}}{\sqrt{2}^2}$$\Leftrightarrow$$T_{B} = \frac{\not{2}\times {680,0}\times \sqrt{2}}{\not{2}}$
$$\color{Navy}{T_{B} = 680\sqrt{2}\,N}$$
Sendo $T_{B}$ uma força inclinada de $45^0$ temos que as suas componentes ortogonais são iguais. Logo:
$$\color{Navy}{T_{By} = 680\sqrt{2}\,N}$$
$$\color{Navy}{T_{Bx} = 680\sqrt{2}\,N}$$
No início do raciocínio, começamos por: $R_{Ax} = \frac{\sqrt{2}}{2}T_{B}$
Substituindo $T_{B}$ pelo valor visto acima, teremos:
$R_{Ax} = \frac{\sqrt{2}}{2}\times {670}\sqrt{2}$$\Leftrightarrow$$\color{Navy}{ R_{Ax}= 680\,N}$
Da equação (II), temos:
$R_{Ay} + R_{Ax} = 1400,0$$\Leftrightarrow$$R_{Ay} + 680,0 = 1400,0$
$$\color{Navy}{R_{Ay}= 720,0\,N}$$
Falta determinarmos a resultante das reações na articulação $A$
$$\color{Sepia}{{R_{A}}^2 = {R_{Ax}}^2 + {R_{Ay}}^2}$$
${R_{A}}^2 = {680}^2 + {720}^2$$\Leftrightarrow$$\sqrt{{R_{A}}^2} = \sqrt{462400 +518400}= 990,35\,N$
$$\color{Navy}{R_{A} = 990,35\, N}$$
Exemplo 6. – Imaginemos um travessão uniforme, suspenso por seu centro de gravidade, podendo girar em torno do eixo que o suspende. Há pequenos engates separados de distâncias uniformes de $d=5,0\,cm$. Massas aferidas de $100,0\,g$, podem ser penduradas nesses engates. Pendurando cinco massas no terceiro engate a partir do centro, quantas massas devemos colocar suspensas no quinto engate no lado oposto, para restabelecer o equilíbrio?
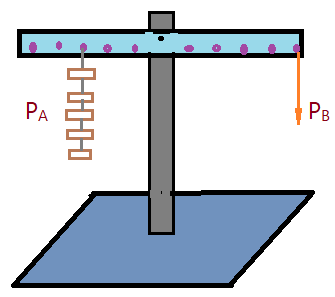
Se a distância entre os engates é $5\,cm$, as cinco massas de $100\,g$ estão a distância em relação ao ponto de suspensão igual a:
$D_{1} = 3\\times 0,05 = 0,15\,m$
$D_{2} = 5\times 0,05 = 0,25\, m$
Considerando a aceleração da gravidade igual a $10,0\, m/s^2$, cada massa terá:
$P = m\times g$$\Leftrightarrow$$ P = 0,10\times 10 = 1,0\,N$
Cinco pesos terão $P_{1}= 1\times 5 = 5,0\,N$
O travessão está suspenso pelo centro de gravidade, o que significa que ele sem nenhum peso, está na condição de equilíbrio horizontal. Determinemos agora o peso que teremos que suspender no quinto engate na outra extremidade.
$\sum_1^2 = 0$$\Leftrightarrow$$ P_{1}\cdot D_{1} + P_{2}\cdot D_{2} = 0$
$ {5,0}\times {0,15} – P_{2}\times {0,25} = 0$$\Leftrightarrow$${0,25}\times P_{2} =\frac{ 0,75}{0,25} = 3,0\,N$
$$\color{Navy}{P_{2} = 3,0\,N}$$
O que nos mostra que conseguiremos equilibrar o travessão, pendurando três massas de $100,0\,g$ no quinto engate.
Essse é o princípio da balança de braços.
Já podemos fazer exercícios individualmente ou em grupo.

01. Uma barra metálica de comprimento igual a $L=1,20\,m$, tem uma massa de $m=15,0\,kg$. A aceleração da gravidade é de $g=10,0\,m/s^2$. Um cabo está fixado na barra a distância de $0,50\,m$ de uma extremidade e a sustenta a uma altura de $h=2m$ do solo. Na ponta mais curta, pendura-se um corpo de peso $P_{1}$ e ela assim fica em equilíbrio horizontal. Determinar o valor do peso pendurado. Observe a figura.
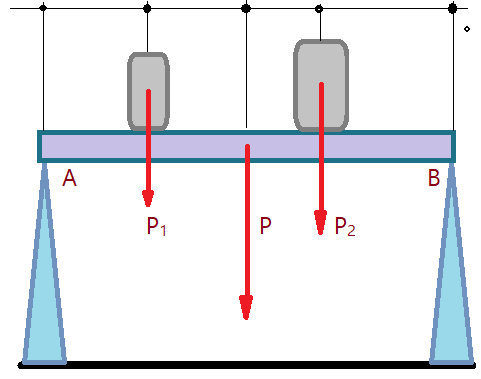
02. Uma barra rígida de $L=1,60\,m$, tem peso de $P=400,0\,N$ e está apoiada sobre dois cutelos em suas extremidades A e B. Um bloco de $P_{1}=240,0\,N$ está apoiado a $0,30\,m$ da extremidade A e outro de $P_{2}=320,0\,N$ está apoiado a $0,50\,m$ da extremidade B. Determine as intensidades da reação nos apoios A e B. Veja a figura.
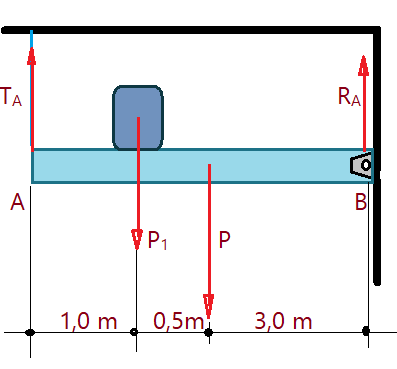
03. Uma barra articulada no extremo $B$, tem massa de $m=100\,kg$ e comprimento de $L=3,0\,m$. A aceleração da gravidade é $g=10,0\,m/s^2$. Um cabo fixado à extremidade A, sustenta a posição da barra na horizontal, aplicando uma força vertical de tração. Um bloco de $m_{1}=50,0\,kg$ é apoiado sobre a barra no ponto correspondendo a $\frac{1}{3}$ do comprimento, a partir da extremidade A. Determine a intensidade da força de tração aplicada na extremidade A, a força de reação na articulação no ponto B. Veja a figura para entender o problema.
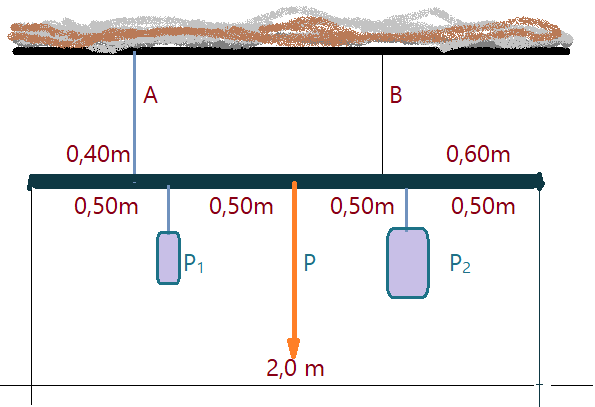
04. Uma barra de $L=2,0\,m$, tem peso de $P=800\,N$ e está suspensa por dois pontos A e B. Dois blocos estão suspensos por cabos presos à barra e seus pesos são $P_{1} =300,0\,N$ e $P_{2}= 500,0\,N$. Os pontos de suspensão estão indicados na figura, junto com as distâncias. Determine as forças de tração nos cabos de sustentação em A e B.
Havendo dúvidas, use um dos canais abaixo para pedir esclarecimentos. Não fique sem pedir ajuda. Estamos às ordens.
Curitiba, 10 de julho de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
