Física – Termologia – Termodinâmica.

Energia térmica.

É a energia associada ao movimento de vibração das partículas materiais (moléculas, átomos, íons, elétrons, células) que compõem o sistema em análise.

Temperatura

É a grandeza macroscópica que avalia o nível de energia interna do sistema. A unidade de medida é o kelvin (K), unidade de temperatura absoluta em concordância com a Teoria Cinética dos Gases.

A Termodinâmica descreve estatisticamente a natureza, ou parte dela. Isso permite entender o comportamento macroscópico dos sistemas constituidos de uma variedade de corpos.

Em face da amplitude da área de abrangência do estudo, torna-se necessário estabelecer alguns conceitos fundamentais, permitindo a compreensão das leis de regem os fenômenos termodinâmicos.

Sistema Termodinâmico

Uma região distinguível de suas vizinhanças dentro do todo da natureza, denominaremos sistema termodinâmico. Esses sistemas podem ser separados por uma parede, uma camada como uma membrana ou outro tipo de dispositivo isolante. Um balão cheio de gás é um sistema termodinâmico.

Sistema fechado é um tipo mais restrito de sistema. Eles não trocam calor (Energia Térmica) ou trabalho entre eles ou a vizinhança.

Estado Termodinâmico

O estado termodinâmico de um sistema é definido por um conjunto de variáveis usadas para descrever as condições do sistema.

Isso permite a qualquer outro experimentador repetir um determinado experimento em qualquer momento posterior.

Variáveis de estado

São as variáveis que usamos para descrever o estado termodinâmico de um sistema. São elas a pressão, o volume, a massa e a temperatura absoluta.

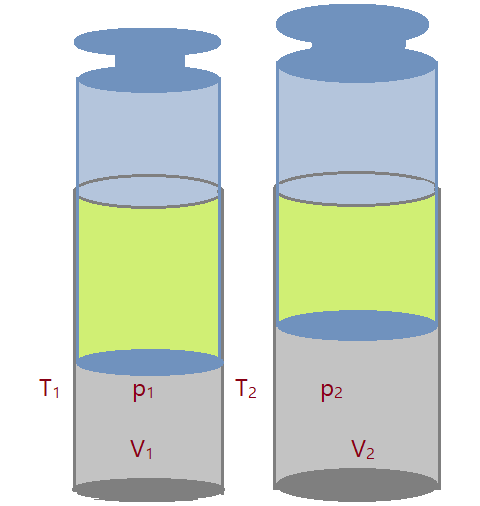
Transformação termodinâmica

É a denominação de toda mudança ocorrida no estado termodinâmico de um sistema, causada pela modificação de duas ou mais de suas variáveis de estado.

Equilíbrio termodinâmico

Os sistemas termodinâmicos via de regra não apresentam tendência natural à mudar seu estado. Para que isso ocorra, deve ocorrer uma influência da vizinhança.

As transformações podem ser de dois tipos:

• Reversíveis, quando a tendência é de retornar ao estado primitivo, quando ele é alterado.
• Irreversíveis, quando o retorno à condição primitiva fica cada vez mais difícil de ocorrer após o deslocamento inicial.

Trabalho termodinâmico

O trabalho termodinâmico ocorre durante as trocas de energia entre dois sistemas termodinâmicos. Isso implica na movimentação de suas fronteiras, com a consequente variação de volume por eles sofridos.

Ao aquecer o gás existente em uma seringa hipodérmica, ou em um pistão, haverá um momento em que a pressão do gás (ar) irá empurrar o êmbolo para fora, aumentando o volume e consequentemente haverá uma queda de temperatura. Sabemos do estudo da mecânica que um deslocamento implica na realização de Trabalho Mecânico.

Sendo assim, fica estabelecida a relação entre a energia térmica e a energia mecânica. Há vários sistemas construídos para a transformação de energia térmica em outra forma de energia, geralmente mecânica, com posterior transformação em outras modalidades. O sistema mais comum é o utilizado na movimentação dos comboios ferroviários, geradores elétricos, máquinas industriais.

Leis da Termodinâmica

São ao todo quatro as leis que regem os fenômenos termodinâmicos. A saber:

• Lei Zero da Termodinâmica – vários corpos em um mesmo ambiente fechado, inicialmente a temperaturas diferentes, trocam calor entre si, até o momento de estabelecer o equilíbrio térmico.
• Primeira Lei da Termodinâmica – a variação da energia interna de um sistema termodinâmico é igual à diferença entre a quantidade de calor e trabalho trocado com a vizinhança.

$$\color{Maroon}{\Delta U = Q – \tau}$$

• Segunda Lei da Termodinâmica – diz respeito à entropia do sistema e mede a aleatoriedade ou desorganização da energia interna do sistema.
• Terceira Lei da Trmodinâmica – o limite inferior da temperatura absoluta é o “zero absoluto” ou seja $0\,K$, esta temperatura é na prática inalcançável aos sistemas termodinâmicos. Consequentemente o rendimento das máquinas térmicas nunca chega aos $100\%$.

Máquinas térmicas

São máquinas que funcionam entre duas fontes chamadas Fonte quente e a outra fonte fria. No início do ciclo o sistema da máquina recebe calor da fonte quente, o vapor se expande empurrando o êmbolo do pistão. Ao final do percurso a sobra de calor é rejeitada para a fonte fria e realiza-se a quarta etapa do ciclo, expulsando o vapor. A repetição desse processo permite obter energia mecânica para mover os mais diferente engenhos de invenção do homem.

Trabalho termodinâmico

$$\color{Maroon}{\tau = Q_{q} – Q_{f}}$$ (1)

Rendimento de máquinas térmicas

$$\color{Maroon}{\eta = \frac{\tau}{Q_{q}}}$$ (2)

$$\color{Maroon}{\eta = 100\times\frac{\tau}{Q_{q}}\%}$$

Substituindo (1) em (2):

$$\color{Maroon}{\eta = \frac{Q_{q} – Q_{f}}{Q_{q}} = 1 – \frac{Q_{f}}{Q_{q}}}$$

$$\color{Maroon}{\eta = 100\times{(1 – \frac{Q_{f}}{Q_{q}})}\%}$$

O rendimento nos informa o percentual de energia térmica convertida em energia mecânica, para aproveitamento de forma util.

O ciclo de uma máquina a vapor (locomotiva, locomóvel, etc) tem esta forma:

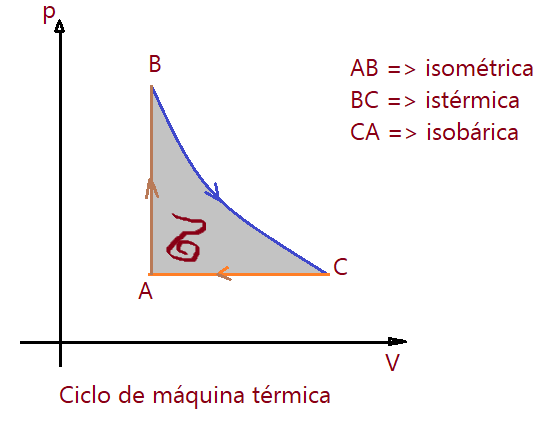
O ciclo sendo percorrido no sentido horário, como indicam as setas na figura, o trabalho é motor ou seja é positivo.

Neste caso também o rendimento é positivo. Se o ciclo for percorrido em sentido anti-horário, o trabalho e rendimento serão negativos.

Obs.: É importante observar que o rendimento geralmente oferecido pelas máquinas térmicas é inferior a taxa de 50%.

Ciclo (ideal) de Carnot

O ciclo termodinâmico de Carnot para uma máquina funcionando entre duas temperaturas “quente” e “fria”, é um modelo ideal, porém irrealizável. É composto por duas transformações isotérmicas e duas adiabáticas. Seu funcionamento depende de alternância entre etapas lentas seguidas de outra extremamente rápidas, o que impede a realização do ciclo. Serve para mostrar o limite superior de rendimento possível entre as temperaturas extremas do ciclo.

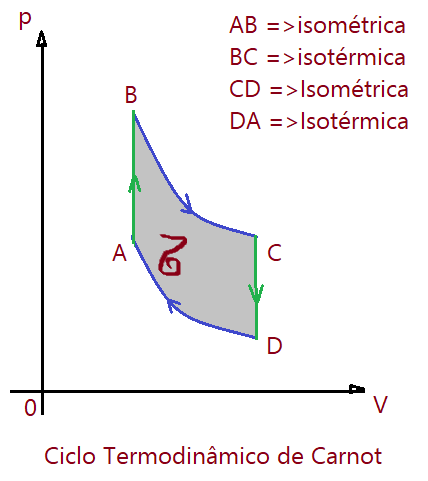
As quantidades de calor trocadas dependem essencialmente das temperaturas, pois a massa é constante, de modo que podemos substituir as quantidades de calor pelas temperaturas absolutas.

A área interna do ciclo sempre representa o módulo do trabalho realizado, seja positivo ou negativo.

$$\color{Maroon}{\eta = \frac{T_{q} – T_{f}}{T_{q}}}$$

$$\color{Maroon}{\eta = 1 – \frac{T_{f}}{T_{q}}}$$

$$\color{Maroon}{\eta=100\times{(1 – \frac{T_{f}}{T_{q}})}\%}$$

Sistemas de refrigeração

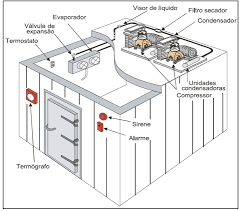
Os sistemas de refrigeração utilizados nos refrigeradores domésticos, sistemas de ar condicionado, congeladores desde os domésticos até os dos grandes frigoríficos, são máquinas térmicas de ciclo anti-horário. Como o calor é uma forma de energia que não se transmite espontaneamente do corpo menos quente para o mais quente, usamos uma forma de forçar o processo.

Todos os sistemas de refrigeração funcionam baseados em um gás, confinado dentro de um ciclo. Na parte externa, em contado com o ar atmosférico, o gás sofre compressão e dissipa a energia térmica que absorveu no interior do aparelho, unto com o trabalho recebido do compressor. Ao ingressar na parte interna do ciclo, passa por uma válvula de expansão. O trabalho realizado ao se expandir, faz a temperatura baixar, permitindo que absorva calor do interior.

Perdendo calor para o gás expandido, o recipiente interno do sistema tem sua temperatura diminuída. Quando esta temperatura atinge o nível em que está graduado o termostato, o sistema de compressão é desligado, voltando a funcionar quando a temperatura subir um pouco. Dessa forma consegue-se manter o nível uniforme de refrigeração. Aqui temos então:

$$\color{Navy}{\Delta U = Q + \tau}$$

1. O calor é retirado da fonte fria e cedido para a fonte quente.
2. O trabalho é adicionado ao calor retirado da fonte fria, para formar o total de calor cedido à fonte quente. Este trabalho é fornecido pelo sistema de compressão.
3. Existem sistemas de refrigeração que usam fontes de calor como queimadores a querosene, a gás combustível, porém o gás refrigerante é outro. São sistemas apropriados para uso em locais onde não exista rede de distribuição de energia elétrica para acionar os compressores. É um sistema mais lento, portanto menos eficiente, usado em situações de necessidade.

O rendimento dos sistemas de refrigeração é portanto negativo, uma vez que o trabalho é fornecido ao sistema e não retirado dele.

$\color{Maroon}{\eta = \frac{-\tau}{Q_{f}}}$$\Leftrightarrow$$\color{Navy}{\eta = 100\times{(\frac{-\tau}{Q_{f}})}\%}$

Substituindo o trabalho por:

$$\color{Maroon}{-\tau = Q_{f} – Q_{q}}$$

$\eta = \frac{Q_{f} – Q_{q}}{Q_{f}}$$\Leftrightarrow$$\color{Navy}{\eta = 1 – \frac{Q_{q}}{Q_{f}}}$

$$\color{Navy}{\eta = 100\times{(1 – \frac{Q_{q}}{Q_{f}})}\%}$$

Vamos exercitar?

01. Uma máquina a vapor funciona entre as temperaturas $\color{Maroon}{\theta_{q}=227^0C}$ e a temperatura ambiente de $\color{Maroon}{\theta_{f} = 27^0C}$. Se ela absorve por ciclo $\color{Maroon}{Q_{q}= 6000\,cal}$ e ao final do ciclo rejeita $\color{Maroon}{Q_{f}=4400\,cal}$. Determinar o rendimento dessa máquina e o trabalho realizado ao final de $\color{Maroon}{\Delta t = 5\,min}$, se a frequência de seu cilindro é de $\color{Maroon}{f = 5\,Hz}$. Ao final calcule o rendimento de uma máquina de Carnot equivalente.

Inicialmente calcularemos as temperaturas absolutas das fontes quente e fria.

$T_{f} = 273 + 27 = 300\,K$

$T_{q} = 273 + 227 = 500\,K$

$Q_{q}= 4,196\times 6000 = 25176 J$

$Q_{f}= 4,196\times 400 = 18462,4J$

O rendimento será:

$\eta = 1 – \frac{Q_{f}}{Q_{q}}$$\Leftrightarrow$$\eta = 1 – \frac{18462,4}{25176}$

$$\color{Maroon}{\eta = 1 – 0,73 = 0,27}$$

$$\color{Maroon}{\eta = 27\%}$$

Se a frequência é de $f=5\,Hz$, a máquina executará:

$n = f\times \Delta t$

$n = 5\times 300 = 1500 ciclos$

$\tau = Q_{q} – Q{f}$$\Leftrightarrow$$\tau = 25176 – 18462,4 = 6713,6\,J/ciclo$

$$\color{Navy}{\tau_{t} = 6713,6\times 1500 = 10070400\,J}$$

Uma máquina de Carnot funcionando entre estas temperaturas daria um rendimento de:

$\eta = 1 – \frac{T_{f}}{T_{q}}$$\Leftrightarrow$$\eta = 1 – \frac{300}{500}$

$$\color{Navy}{\eta = 1 – 0,60 = 0,4}$$

$$\color{Navy}{\eta = 40\%}$$

Para as temperaturas dadas no enunciado não há forma de uma máquina térmica alcançar rendimento de 40%, quanto mais ultrapassar esse valor.

02. Se uma máquina térmica funciona entre as temperaturas de $\color{Maroon}{7^0C}$ e $\color{Maroon}{307^0C}$. Qual é o seu rendimento no ciclo de Carnot? Para que ela forneça um trabalho motor de $\color{Maroon}{\tau = 4,19\times 10^5\,J}$, qual é o total de energia absorvida da fonte quente? Qual é o total de energia rejeitada para a fonte fria?

$\eta = 1 – \frac{T_{f}}{T_{q}}$$\Leftrightarrow$$\eta = 1 – \frac{280}{580}$

$\color{Maroon}{\eta = 1 – 0,48 = 0,52}$$\Leftrightarrow$$\color{Navy}{\eta = 52\%}$

$\eta = \frac{\tau}{Q_{q}}$$\Leftrightarrow$$0,52 = \frac{4,19\times 10^5}{Q_{q}}$

$Q_{q}= \frac{4,19\times 10^5}{0,52}$$\Leftrightarrow$$Q_{q} = 805.769,23\,J$

$$\color{Maroon}{Q_{q} = 8,06\times 10^5\,J}$$

Vamos exercitar por conta.

01. Certa máquina térmica recebe 500 J de calor e realiza um trabalho de 125 cal. Sendo 1 cal = 4 J, marque a alternativa correta.

a) Essa máquina contraria a primeira lei da Termodinâmica.

b) A máquina não contraria a segunda lei da Termodinâmica.

c) O rendimento dessa máquina é de 25%.

d) A máquina não contraria a primeira lei da Termodinâmica, que trata sobre a conservação da energia.

e) Como o rendimento da máquina é de 25%, podemos afirmar que ela não contraria a primeira lei da Termodinâmica.

02. (ITA) Uma máquina térmica opera segundo o ciclo JKLMJ mostrado no diagrama T-S da figura.

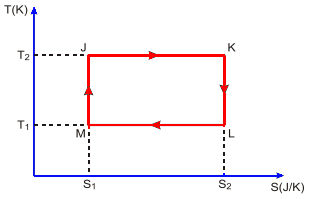
Pode-se afirmar que:

a) processo JK corresponde a uma compressão isotérmica;

b) o trabalho realizado pela máquina em um ciclo é W = (T₂ – T₁)(S₂ – S₁);

c) o rendimento da máquina é dado por η = 1 – T₂/T_1.

d) durante o processo LM, uma quantidade de calor Q_LM = T₁(S₂ – S₁) é absorvida pelo sistema.

e) outra máquina térmica que opere entre T₂ e T₁ poderia eventualmente possuir um rendimento maior que a desta.

03. (UNAMA) Um motor de Carnot cujo reservatório à baixa temperatura está a $7,0^0C$ apresenta um rendimento de$\eta= 30\%$. A variação de temperatura, em Kelvin, da fonte quente a fim de aumentarmos seu rendimento para $50\%$ será de:

a) 400;

b) 280;

c) 160;

d) 560;

e) 480.

04. A respeito da primeira lei da Termodinâmica, marque a alternativa incorreta:

a) Em uma transformação isotérmica, a variação da energia interna é nula.

b) A primeira lei da Termodinâmica trata da conservação da energia.

c) Em uma transformação isocórica, não haverá realização de trabalho;

d) Em uma transformação adiabática, o trabalho será realizado sobre gás quando a variação da energia interna é positiva;

e) A primeira lei da Termodinâmica diz que o calor fornecido a um gás é igual à soma do trabalho realizado pelo gás e a sua variação da energia interna.

05. (Uema) – Sobre um sistema realiza-se um trabalho de $\tau=3 000\,J$ e, em resposta, ele fornece $Q = 500\,cal$ de calor durante o mesmo intervalo de tempo. A variação de energia interna do sistema durante esse processo é:
(Dado: $1\,cal =4,2\, J$.)

a) 2 500 J;
b) 2900 J;
c) 900 J;
d) 2 100 J;
e) 22 100 J.

06. (Mackenzie-SP) Um gás, contido em um recipiente dotado de um êmbolo que pode se mover, sofre uma transformação.
Nessa transformação fornecemos $Q = 800\,cal$ ao gás e ele realiza o trabalho de $\tau = 209\, J$. Sendo $1\,cal=4,18\,J$, o aumento da energia interna desse gás foi de:

a) 209 J;
b) 3 135 J;
c) 3 344 J;
d) 3 553 J;
e) 3 762 J.

07. (Vunesp-SP) A energia interna U de uma certa quantidade de gás, que se comporta como gás ideal, contida em um recipiente, é proporcional à temperatura T, e seu valor pode ser calculado utilizando a expressão $U=12,5T$. A temperatura deve ser expressa em kelvin e a energia, em joules. Se inicialmente o gás está à temperatura $T =300\,K$ e, em uma transformação a volume constante, recebe $Q= 1 250\,J$ de uma fonte de calor, sua temperatura final será:

a) 200 K;
b) 300 K;
c) 400 K;
d) 600 K;
e) 800 K.

08. Em um processo a pressão constante de $p = 2,0 .10^5\,N/m^2$, um gás aumenta seu volume de $V_{0}= 8.10^{-6}\,m^3$  para $V_{1} = 13.10^{-6}\,m^3$. Calcule o trabalho realizado pelo gás.

09.Um gás sofre uma transformação isobárica sob pressão de $p= 1 000 N/m^2$. Determine o trabalho realizado sobre o gás, quando o volume passa de$V_{0}=8 000\,cm^3$ para de $V =3 000\,cm^3$.

10. (UF – RN) – Dentro de uma sala com ar condicionado, a temperatura média é de $17 ^0C$. No corredor ao lado da sala, a temperatura média é $27^0C$. Tanto a sala quanto o corredor estão a mesma pressão.
Sabe-se que num gás, a energia cinética média das partículas que o compõem é proporcional à temperatura e que sua pressão é proporcional ao produto da temperatura pelo número de partículas por unidade de volume.

Com base nesses dados, pode-se afirmar que:

a) a energia cinética média das partículas que compõem o ar é maior no corredor, e o número de partículas por unidade de volume é menor na sala.

b) A energia cinética média das partículas que compõem o ar é maior no corredor, e o número de partículas por unidade de volume é maior na sala.

c)  A energia cinética média das partículas que compõem o ar é maior na sala, e o número de partículas por unidade de volume é maior no corredor.

d) A energia cinética média das partículas que compõem o ar é maior na sala, e o número de partículas por unidade de volume é menor no corredor.

e) É impossível determinar qualquer relação entre a energia e o número de partículas em qualquer um dos ambientes.

11. (ITA-SP) – Considere uma mistura de gases H_{2}  e N_{2}, em equilíbrio térmico. Sobre a energia cinética média e sobre a velocidade média das moléculas de cada gás, pode-se concluir que:

a) as moléculas de H_{2}  e N_{2} tem a mesma energia cinética média e a mesma velocidade média.

b) Ambas tem a mesma velocidade média, mas as moléculas de N_{2} tem maior energia cinética média.

c) Ambas tem a mesma velocidade média, mas as moléculas de H_{2} tem maior energia cinética média.

d) Ambas tem a mesma energia cinética média, mas as moléculas de N_{2} tem maior velocidade média.

e) Ambas tem a mesma energia cinética média, mas as moléculas de H_{2}  tem maior velocidade média.

12. Determine qual o trabalho realizado por um gás em expansão, que teve seu volume alterado de $5\times 10^{-6}m^3$ para $10\times 10^{-6}\,m^{^3}, em uma transformação à pressão constante de $4\times 10^5\,N/m^2$.

13. Em uma transformação isobárica, um gás realizou um trabalho mecânico de $\tau = 1\times 10^4\,J$ sob uma pressão de $ p = 2\times 10^5\,N$. Se o volume inicial do gás é de $V_{0}= 6\,m^3$, qual o seu volume final após a expansão?

14. (Med. Taubaté-SP) Considere as afirmações abaixo:

l. Em uma transformação isobárica não varia a pressão.
ll. Em uma transformação isocórica não varia o volume.
lll. Em uma transformação isométrica não varia a temperatura.

Com relação às três afirmações acima, podemos dizer que…
a) apenas l é verdadeira;
b) apenas ll é verdadeir;
c) apenas lll é verdadeira;
d) l e ll são verdadeiras;
e) todas são verdadeiras.

15. (FAM-SP) – Se a energia cinética média das moléculas de um gás aumentar e o volume permanecer constante:

a) a pressão do gás aumentará e a sua temperatura permanecerá constante;
b) a pressão permanecerá constante e a temperatura aumentará;
c) a pressão e a temperatura aumentarão;
d) a pressão diminuirá e a temperatura aumentará;
e) a temperatura diminuirá e a pressão permanecerá constante.

16. (UECE) – Do ponto de vista da primeira lei da termodinâmica, o balanço de energia de um dado sistema é dado em termos de três grandezas:

a) pressão, volume e temperatura.
b) calor, energia interna e volume.
c) trabalho, calor e energia interna.
d) trabalho, calor e densidade.

17. (UEFS BA/2017) – A primeira lei da termodinâmica para sistemas fechados foi originalmente comprovada pela observação empírica, no entanto é hoje considerada como a definição de calor através da lei da conservação da energia e da definição de trabalho em termos de mudanças nos parâmetros externos de um sistema.

Com base nos conhecimentos sobre a Termodinâmica, é correto afirmar:

a) A energia interna de uma amostra de um gás ideal é função da pressão e da temperatura absoluta.
b) Ao receber uma quantidade de calor Q igual a 48,0J, um gás realiza um trabalho igual a 16,0J, tendo uma variação da energia interna do sistema igual 64,0J.
c) A energia interna, o trabalho realizado e a quantidade de calor recebida ou cedida independem do processo que leva o sistema do estado inicial A até um estado final B.
d) Quando se fornece a um sistema certa quantidade de energia Q, esta energia pode ser usada apenas para o sistema realizar trabalho.
e) Nos processos cíclicos, a energia interna não varia, pois volume, pressão e temperatura são iguais no estado inicial e final.

18. (Ufpa) – Um técnico de manutenção de máquinas pôs para funcionar um motor térmico que executa 20 ciclos por segundo. Considerando-se que, em cada ciclo, o motor retira uma quantidade de calor de $Q_{q}=1200\,J$ de uma fonte quente e cede $Q_{f}=800\,J$ a uma fonte fria, é correto afirmar que o rendimento de cada ciclo é

a) 13,3%;
b) 23,3%;
c) 33,3%;
d) 43,3%;
e) 53,3%.

19. (IFG) – As máquinas térmicas são dispositivos que operam sempre em ciclos, isto é, retornam periodicamente às condições iniciais. Uma maneira de estudá-las é por meio de transformações que ocorrem dentro destes ciclos, representados por um gráfico do comportamento da pressão de um gás de trabalho em função do volume por ele ocupado.

O gráfico a seguir representa um ciclo de uma máquina térmica realizado por um sistema gasoso:

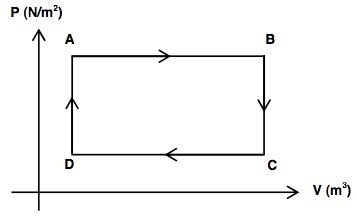
Analise as afirmativas.

I. De A para B ocorre uma expansão isobárica.
II. De B para C o trabalho é motor, ou seja, realizado pelo sistema.
III. A variação de energia interna no ciclo ABCDA é positiva.
IV. No ciclo fechado, ABCDA, não há variação de energia interna e o trabalho total é nulo.

Está(ão) correta(s).

a) Apenas a afirmativa I.
b) Apenas as afirmativas I e II.
c) Apenas as afirmativas I e IV.
d) Apenas as afirmativas I, II e III.
e) Apenas as afirmativas I, II e IV.

20. (UFRS) – Qual é a variação de energia interna de um gás ideal sobre a qual é realizado um trabalho de 80J, durante uma compressão adiabática?

a) 80 J
b) 40 J
c) zero
d) – 40 J
e) – 80 J

Havendo dúvidas, peça ajuda por um dos canais abaixo relacionados. Estou aqui para ajudar no que for possível.

Curitiba, 19 de julho de 2010

Décio Adams

[email protected]  

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@DcioAdams

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732

Tags: #Ciclo de Carnot, #equilíbrio térmico, #fonte fria, #fonte quente, #gases perfeitos, #máquina térmica, #rendimento, #termodinâmica, #variáveis de estado