Física – Mecânica – Dinâmica. Impulso de uma força
O uso da palavra Impulso é bem frequente, mas na maioria das vezes tem sentido figurado, ou pelo menos, não é no sentido que lhe atribuímos aqui, no estudo da física.
Qual é a diferença?
É comum dizermos:
- Eu senti um impulso e fui lá fazer o que fiz. Nesse caso queremos dizer que tivemos vontade, desejo de fazer algo.
No estudo da Mecânica, essa palavra tem um significado bem mais concreto. Quando aplicamos uma força sobre determinado corpo, durante um certo tempo, transmitimos ao corpo um impulso. Podemos notar que estão presentes duas coisas. Uma força e um intervalo de tempo. Facilmente percebemos que o impulso transmitido será tanto maior quanto maior for a intensidade da força e quanto maior for o intervalo de tempo. Isto significa que ele é diretamente proporcional a essas duas grandezas. Estamos portanto definindo uma nova grandeza.
Impulso é o produto da intensidade da força pelo intervalo de tempo em que ela atua.
$$\color{Indigo}{\vec{I} = \vec{F}\times\Delta t}$$
Temos pois uma grandeza vetorial, resultante do produto de uma grandeza vetorial por uma escalar. Toda grandeza vetorial fica determinada pelo seu módulo, sua direção e sentido. No caso do impulso, temos:
Módulo: é o produto do módulo da força pelo intervalo de tempo.
Direção e sentido: são iguais à direção e sentido da força.
Falta estabelecer as unidades em que ele será medido.
No SI: $F = newton(N)$ e $\Delta t = segundo(s)$. Logo o impulso resulta da multiplicação dessas unidades.
$$\color{Navy}{I = N\times s}$$
No antigo CGS, usaríamos: dyn e s.
$$\color{Navy}{I = dyn\times s}$$
No sistema Técnico: kgf e s
$$\color{Navy}{I = kgf\times s}$$
Observação: Nenhum nome de cientista ou pesquisador foi associado à unidade de impulso.
Representação gráfica de I = f(t).
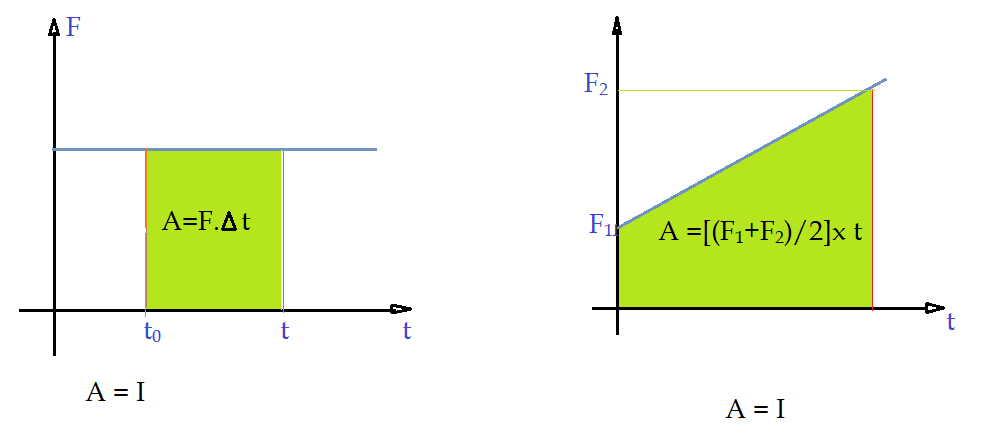
Na hipótese de aplicar força constante, o gráfico resulta em um quadrilátero, cuja área é numericamente igual ao impulso. Se a força for variável, a área compreendida sob a curva é igualmente igual ao impulso. Isso nos auxilia na resolução de problemas.
Quantidade de movimento.
Vimos que a força agindo sobre o corpo, transmite a ele um impulso. Este impulso poderá gerar uma aceleração, fazendo o corpo aquirir determinada velocidade, ou variar sua velocidade para mais ou para menos. Já estudamos uma grandeza relacionada a isso, que é o Trabalho Mecânico.
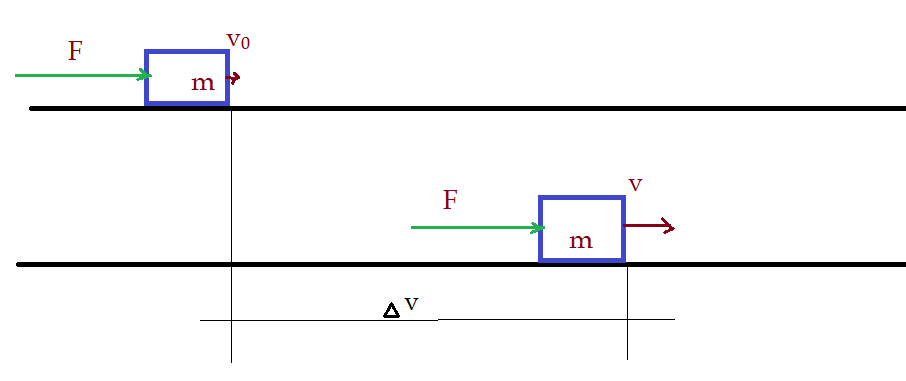
Mas há outra grandeza que é muito prática na solução de certos problemas e recebe o nome Quantidade de movimento.
A quantidade de movimento também é vetorial e está associada com a massa e a velocidade do corpo. Quanto maiores forem essas grandezas, maior a quantidade de movimento. Portanto, é diretamente proporcional.
Quantidade de movimento é o produto da massa do corpo pela sua velocidade.
$$\color{Indigo}{\vec{q} = m\times \vec{v}}$$
Direção e sentido: são iguais à direção e sentido da velocidade do corpo.
Na figura acima, podemos observar que o corpo tem, no instante inicial, uma pequena velocidade, que lhe confere uma quantidade de movimento inicial:
$$\color{Navy}{\vec{q_{0}} = m\times\vec{v_{0}}}$$
No final, vemos que a velocidade sofreu um aumento e teremos uma quantidade de movimento maior. Esse aumento está associado ao impulso da força F.
$$\color{Navy}{\vec{q} = m\times\vec{v}}$$
É fácil demonstrar que a variação da quantidade de movimento é igual ao impulso da força aplicada.
$\Delta q = q – q_{0}$$\Leftrightarrow$$ m\times\Delta v = mv – mv_{0}$=$m\times{\left(v – v_{0}\right)}$
Note que: $\vec{I} =\vec{F}\times\Delta t$$\Leftrightarrow$$\vec{I}=m\times \vec{a}\times\Delta t$
$\vec{I} = m\times\left(\frac{v -v_{0}}{\Delta t}\right)\times\Delta t$
$$\vec{I} = m\times\left({v -v_{0}}\right)$$
Fica assim demonstrado que $$\Delta q = I$$
O que acabamos de demonstrar, é conhecido normalmente como o Teorema da Impulsão ou da quantidade de movimento.
Teorema da Impulsão ou da Quantidade de movimento.
Fica assim enunciado:
O impulso transmitido a um corpo é igual à sua variação da quantidade de movimento.
Unidades de quantidade de movimento:
No SI: $\color{Navy}{q = kg\times\frac{m}{s}}$
No CGS: $\color{Navy}{q= g\times\frac{cm}{s}}$
No MKgfS (técnico): $\color{Navy}{q = utm\times\frac{m}{s}}$
Hora de exercitar.
01. Em um clássico do futebol goiano, um jogador do Vila Nova dá um chute em na bola aplicando-lhe uma força de intensidade $ F =7\times{10}^{2}\,N $ num intervalo de $ \Delta t = {0,1}\,s$ em direção ao gol do Goiás e o goleiro manifesta reação de defesa ao chute, mas a bola entra para o delírio da torcida. Determine a intensidade do impulso do chute que o jogador dá na bola para fazer o gol.
O problema não fala na distância, pois provavelmente ela é dispensável. A menção do goleiro de defender também não tem importância, pois o impulso resultante do chute não depende desses fatos. Precisamos apenas a intensidade da força e o tempo de ação da mesma.
$F = 7\times{10}^2\,N$ e $\Delta t = {0,1}\,s$
$$I = F\times\Delta t$$
$$I = 7\times{10}^2\times {0,1}= 70\,N\times s $$
02. Sobre uma partícula de massa $m={8,0}\,kg $, movendo-se à $v_{0} ={25,0}\,m/s$, passa a atuar uma força constante de intensidade $F = {2,0}\times{10}^2\,N$ durante o intervalo de tempo $\Delta t = 3,0\,s $ no mesmo sentido do movimento. Determine a quantidade de movimento desta partícula após o término da ação da força. Depois determine a velocidade final do corpo.
O Teorema da Impulsão nos informa que:
$I = \Delta q$$\Leftrightarrow$$F\times\Delta t = {q – q_{0}}$
$${2,0}\times{10}^2\times {3,0} = {q – {8,0}\times{25,0}}$$
$${6,0}{10}^2 = {q – 200,0}$$
$$q = 200,0 + 600,0 = 800,0 kg\times\frac{m}{s}$$
A velocidade final: $$q = m\times v$$
$$800,0 = {8,0}\times v$$
$$v = \frac{800,0}{8,0}= 100,0\frac{m}{s}$$
03. Em um ponto material é aplicada uma força de intensidade$F ={ 5,4}\times{10}^2\,N$, durante um intervalo de tempo igual a $\Delta t ={ 1,1}\times{10}^{-1}\,s$. Determine a intensidade do impulso da força aplicada no ponto material.
Aqui iremos aplicar diretamente a equação do impulso.
$F= {5,4}\times{10}^2\,N$ e $\Delta t = {1,1}\times{10}^{-1}\,s$
$$I = F\times\Delta t$$
$$I= {5,4}\times{10}^2\times{1,1}\times{10}^{-1}$$
$$I = {5,4}\times{1,1}\times{10} = 59,4 N\times s$$
04. Seja uma pequena esfera de massa $m = 2,0\,kg $, que em um determinado instante apresenta uma velocidade horizontal, orientada da esquerda para a direita e de módulo igual a $v = 5,0\,m/s$. Determine o módulo, a direção e o sentido da quantidade de movimento dessa esfera.
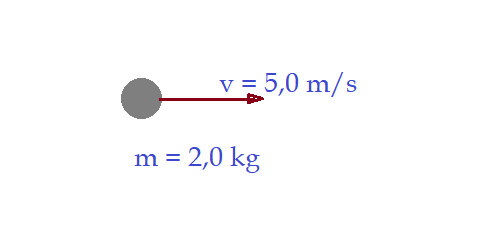
Módulo:
$q = m\times v$
$q = {2,0}\times {5,0}=10,0 kg\times\frac{m}{s}$
A direção e o sentido da quantidade de movimento são os mesmos da velocidade, ou seja, horizontal, da esquerda para direita.
Vamos treinar um pouco sozinhos!
01. Determine, em $kg m/s$, o valor da quantidade de movimento dos seguintes corpos:
a) Uma bola de futebol, de massa$m={0,4}\,kg$, chutada a uma velocidade de $v = {30,0}\,m/s$.
b) Um automóvel de massa de uma tonelada, deslocando-se à velocidade de $v = {72}\,km/h$.
c) Uma bala de fuzil, de massa de$m= {10}\,g$, à velocidade $v ={800,0}\,m/s$.
02. A que velocidade uma pessoa de $m={80}\,kg$ deveria se deslocar para possuir a mesma quantidade de movimento da bala de fuzil ( letra c ) do exercício anterior?
03. Considere um corpo de massa $m=2\,kg$, em repouso sobre uma superfície horizontal. Sobre ela age uma força constante, de módulo $F=6\,N$, durante $\Delta t = 3\,s$. No final desse tempo, o corpo apresenta velocidade de $V_{f}=9\,m/s$. Determine:
- a quantidade de movimento inicial;
- a quantidade de movimento final;
- a variação da quantidade de movimento;
- o impulso da força durante os 3 segundos de atuação;
- a aceleração causada pela força aplicada;
- a distância percorrida durante os 3 segundos.
04. Ao bater um pênalti, um jogador de futebol dá um chute em que a bola, de massa $\color{Sepia}{m =420\,g$, sai com velocidade de $\color{Sepia}{v = 30\,m/s$. Supondo que o tempo de contato entre o pé do jogador e a bola seja de $\color{Sepia}{\Delta t = 0,05\,s}$, determine a força que foi exercida pelo jogador sobre a bola.
05. Suponha que um caminhão, que trafegava à velocidade $\color{Sepia}{v}$ colidiu com um carro de massa $\color{Sepia}{m_{cr}=1500\,kg}$ que estava parado no semáforo. Após a colisão, ambos saíram a $\color{Sepia}{v=5\,m/s}$. Sabendo que a massa do caminhão era de $\color{Sepia}{m_{ca}= 6000\,kg$, e que a colisão durou $\color{Sepia}{\Delta t =0,2\,s}$, determine:
- a qual velocidade o caminhão trafegava;
- qual a força que o caminhão fez no carro;
- qual a força que o carro fez no caminhão.
06. Um trenó de massa $\color{Sepia}{m_{t}=40\,kg}$ desliza a uma velocidade de $\color{Sepia}{v_{t}=5,0\,m/s}$, próximo e paralelamente ao peitoril da pista de patinação. Uma pessoa que está em repouso do lado de fora da pista, solta uma mochila de $\color{Sepia}{m_{m}=10\,kg}$, sobre o trenó. Qual a velocidade do trenó após receber a mochila?
07. (Udesc) – O airbag e o cinto de segurança são itens de segurança presentes em todos os carros novos fabricados no Brasil. Utilizando os conceitos da Primeira Lei de Newton, de impulso de uma força e variação da quantidade de movimento, analise as proposições.
I. O airbag aumenta o impulso da força média atuante sobre o ocupante do carro na colisão com o painel, aumentando a quantidade de movimento do ocupante.
II. O airbag aumenta o tempo da colisão do ocupante do carro com o painel, diminuindo assim a força média atuante sobre ele mesmo na colisão.
III. O cinto de segurança impede que o ocupante do carro, em uma colisão, continue se deslocando com um movimento retilíneo uniforme.
IV. O cinto de segurança desacelera o ocupante do carro em uma colisão, aumentando a quantidade de movimento do ocupante.
Assinale a alternativa correta:
( )a) Somente as afirmativas I e IV são verdadeiras;
( )b) Somente as afirmativas II e III são verdadeiras;
( )c) Somente as afirmativas I e III são verdadeiras;
( )d) Somente as afirmativas II e IV são verdadeiras;
( )e) Todas as afirmativas são verdadeiras.
08. (PUC-RJ) – Um jogador de tênis, durante o saque, lança a bola verticalmente para cima. Ao atingir sua altura máxima, a bola é golpeada pela raquete de tênis e sai com velocidade de $\color{Sepia}{v= 108\,km/h}$ na direção horizontal.
Calcule, em $kg.m/s$, o módulo da variação de momento linear da bola entre os instantes logo após e logo antes de ser golpeada pela raquete.
Dado: considere a massa da bola de tênis igual a $\color{Sepia}{m=50\,g}$.
( )a) 1,5;
( )b) 5,4;
( )c) 54;
( )d) 1500;
( )e) 5400.
09. (UECE) – Considere uma esfera muito pequena de massa igual a 1 kg deslocando-se a uma velocidade de 2 m/s sem girar durante 3 s. Nesse intervalo de tempo, o momento linear dessa partícula é:
( )a) $2\,kg.m/s$;
( )b) $3\,s$;
( )c) $6\,kg.m/s$;
( )d) $6\,m$;
( )e $5,5\,kg m/s$.
10. Sobre uma partícula de $\color{Sepia{m = 8\,kg}$, movendo-se à $\color{Sepia}{v_{o}=25\,m/s}$, passa a atuar uma força constante de intensidade $\color{Sepia}{F = 2,0.10^{2}N}$ durante $\Delta t = 3\,s}$ no mesmo sentido do movimento. Determine a quantidade de movimento desta partícula após o término da ação da força.
11. Com base no gráfico, determine o impulso produzido pela força no intervalo de tempo de 0 a 5s.
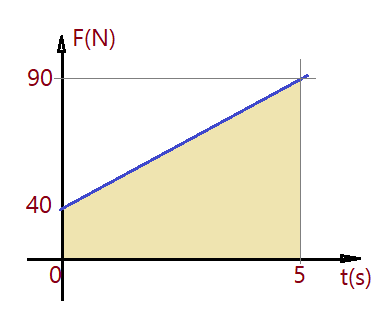
| 12. (Fuvest-SP) – Considere as seguintes afirmações acerca de uma colisão inelástica de um sistema constituído por dois corpos. I. Existe conservação de energia cinética imediatamente antes e imediatamente após a colisão. II. Existe conservação da quantidade de movimento imediatamente antes e imediatamente após a colisão. III. Conserva-se a velocidade relativa dos corpos, antes e após a colisão.Destas afirmações: ( )a) apenas I é correta; ( )b) apenas II é correta; ( )c) apenas III é correta; ( )d) I e II são corretas; ( )e) II e III são corretas. |
13. (Fuvest-SP) Um carro de massa 800 kg, em repouso, é abalroado por trás por um outro de 1 200 kg que se movimenta com velocidade 72 km/h. Supondo que a colisão tenha sido totalmente inelástica, determinar:
a) a velocidade do conjunto constituído pelos dois carros imediatamente após a colisão (em km/h).
b) a variação de energia cinética do sistema.
14. (Unicamp-SP) Um objeto de massa m1=4,0 kg e velocidade v1=3,0 m/s choca-se com um objeto em repouso, de massa m2=2,0 kg. A colisão ocorre de forma que a perda de energia cinética é máxima, mas consistente com o princípio da conservação da quantidade de movimento.
a) Quais as velocidades dos objetos imediatamente após a colisão?
b) Qual a variação da energia cinética do sistema?
15. Em um ponto material é aplicada uma força de intensidade $\color{Sepia}{F = 5,4 \times 10^{2}\, N}$, durante um intervalo de tempo igual a $\color{Sepia}{\Delta t = 1,1 \times 10^{-1}\,}$s. Determine a intensidade do impulso da força aplicada no ponto material.
16. (PUC-RJ) – Um garoto de massa $\color{Sepia}{m_{g} = 30\,kg}$ está parado sobre uma grande plataforma de massa $\color{Sepia}{m_{p}=120\, kg}$, também em repouso em uma superfície de gelo. Ele começa a correr horizontalmente para a direita, e um observador, fora da plataforma, mede que sua velocidade é de $\color{Sepia}{v_{g}=2,0\,m/s}$. Sabendo que não há atrito entre a plataforma e a superfície de gelo, a velocidade com que a plataforma se desloca para a esquerda, para esse observador, é, em $m/s$:
( )a) 1,0;
( )b) 2,0;
( )c) 0,5;
( )d) 8,0;
( )e) 4,0.
17. Um nadador está em pé sobre uma prancha colocada na proa de um pequeno barco. O barco tem uma massa $\color{Sepia}{m_{b}= 300,0\,kg}$. O nadador tem massa de $\color{Sepia}{m_{n}=80,0\,kg}$ e salta para a água com velocidade horizontal de $\color{Sepia}{v_{n}= 3,0\,m/s}$. Qual é a velocidade de recuo do barco logo após o salto? Desconsidere a resistência da água ao movimento do barco.
18. (FAMEMA-SP) – Um brinquedo consiste em um fole acoplado a um tubo plástico horizontal que se encaixa na traseira de um carrinho, inicialmente em repouso. Quando uma criança pisa no fole, comprimindo-o até o final, o ar expelido impulsiona o carrinho.
Considere que a massa do carrinho seja de $\color{Sepia}{m_{c}= 300\,g}$, que o tempo necessário para que a criança comprima completamente o fole seja de $\color{Sepia}{\Delta t = 0,2\,s}$ e que, ao final desse intervalo de tempo, o carrinho adquira uma velocidade de $\color{Sepia}{v_{c}=8\,m/s}$. Admitindo desprezíveis todas as forças de resistência ao movimento do carrinho, o módulo da força média ($F_{méd}$) aplicada pelo ar expelido pelo tubo sobre o carrinho, nesse intervalo de tempo, é igual a:
( )a) 10 N;
( )b) 14 N;
( )c) 12 N;
( )d) 8 N;
( )e) 16 N.
19. Quanto tempo deve agir uma força de intensidade $\color{Sepia}{F=100\,N}$ sobre um corpo de massa igual a $\color{Sepia}{m = 20\,kg}$, para que sua velocidade passe de $\color{Sepia}{v_{0} =5\,m/s}$ para $\color{Sepia}{v =15\,m/s}$?
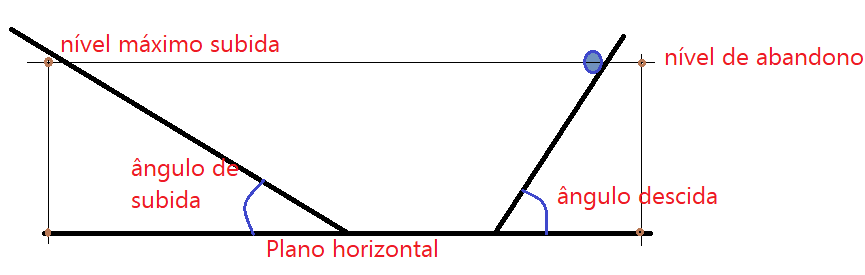
Se o ângulo de inclinação do plano de subida for reduzido a zero, a esfera:
( )a) manterá sua velocidade constante, pois o impulso resultante sobre ela será nulo;
( )b) manterá sua velocidade constante, pois o impulso da descida continuará a empurrá-la;
( )c) diminuirá gradativamente a sua velocidade, pois não haverá mais impulso para empurrá-la.;
( )d) diminuirá gradativamente a sua velocidade, pois o impulso resultante será contrário ao seu movimento;
( )e) aumentará gradativamente sua velocidade, pois não haverá nenhum impulso contrário ao seu movimento.
Darei prosseguimento a esse assunto no post que virá na sequência, onde abordaremos as colisões e aplicaremos muito esses conceitos vistos aqui. Alguma dúvida, peça ajuda por um dos canais abaixo.
Curitiba, 02 de fevereiro de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
