Física – Mecânica – Gravitação Universal
Atração gravitacional
De 03 de janeiro de 1643 até 31 de março de 1727, o mundo teve entre seus seres humanos um dos mais brilhantes cientistas de todos os tempos. Seu nome Sir Isaac Newton. Em sua biografia encontramos passagens em diversas áreas das ciências, inclusive no Cálculo Matemático. Seu maior destaque fica por conta de suas pesquisas no campo da física. Já estudamos as denominadas Três Leis de Newton, da mecânica geral. Mas seu gênio não parou por aí. Deve-se à sua perspicácia e capacidade de observação uma das mais importantes leis que regem o Universo. Estamos falando da Lei de Gravitação Universal.
Há várias lendas a respeito de fatos que teriam levado o genial cientista às conclusões, mas a verdade não reside aí. Foi sua análise das Leis de Kepler dos movimentos planetários, aliada à observações de sua própria autoria, que levaram Isaac Newton a nos brindar, levantando a cortina desse mundo fantástico, antes tido como inexistente ou explicado com as mais variadas elucubrações. Tentava-se explicar os movimentos celestes por uma coisa denominada “vórtice”, carente de fundamentação teórica e prática. Após longas meditações, observações e análises matemáticas, Newton chegou ao enunciado daquela Lei Natural, que se aplica a todo universo. Enunciado da Lei de Gravitação. É possível que a famosa lenda da maçã, aquela que teria caído da macieira em sua cabeça, tenha lhe servido de ponto de interrogação. Se ele já havia estabelecido as leis dos movimentos, onde temos que a força e a aceleração resultante são proporcionais, deveria ocorrer algo semelhante com a maçã. Se ela estava ligada ao galho da macieira e em dado momento se desprendia, precipitando-se para o solo em movimento acelerado, é forçoso haver uma força que provoca esse efeito. Qual a origem da força? A conclusão foi o que segue:
- “Matéria atrai matéria, na razão direta do produto das suas massas e na razão inversa do quadrado da distância entre elas”.
O que Newton não conseguiu estabelecer foi a constante de proporcionalidade existente entre essas grandezas. Essa constante, denominada Constante de gravitação universal, foi determinada por Cavendish, com sua balança de torção, quase um século depois. Pelo menos é isso que grande parte dos livros diz, porém, o objetivo de Cavendish, com um projeto de seu amigo Michell, falecido antes da conclusão, era determinar a densidade da Terra. Em outras palavras, “pesar a Terra”. Depois de diversas medições, publicou nas Phisycal Transactions da Royal Society, o valor $5,48\pm0,038$ vezes a densidade da água. Posteriormente, foi encontrado um erro de aritmética em seus cálculos e com os mesmos dados determinou-se o valor $5,448\pm0,033$ vezes a densidade da água. Hoje o valor aceito é $5,53$ vezes. Aproximadamente 100 anos depois dos experimentos de Cavendish, cerca de $200\,anos$ após o enunciado de Newton da Lei de Gravitação, com uso dos mesmos recursos, foi usado pela primeira vez o valor da Constante de Gravitação Universal. Seu valor geralmente usado é:
$$\color{Brown}{G = 6,674181\times{10}^{-11} m^3\times kg^{-1}\times s^{-2}}$
Na resolução de exercícios habitualmente usamos o valor ${G=6,67\times {10}^{-11} m^3\times kg^{-1}\times s^{-2}}$
A divulgação da Lei de Gravitação por Newton causou um considerável alvoroço nos meios científicos da época. Os adeptos da teoria dos “vórtices” e outros menos preocupados com experimentações ou observações, no início rejeitaram tal princípio. Havia dificuldade em admitir a ação exercida à distância, sem uma ligação física entre dois corpos. Aqueles que buscaram entender suas implicações constataram que as Leis de Johannes Kepler dos movimentos planetários, tornavam-se mais aceitáveis e explicáveis sob esse ponto de vista. Parece que essa é uma das razões da demora em determinar a constante de proporcionalidade que Newton previa, mas não demonstrara preocupação em obter seu valor. Existe vasta literatura bibliográfica nas bibliotecas e disponível em diversos sites da internet a respeito dos detalhes históricos que envolveram cada uma das etapas do processo de aceitação e comprovação dessas teorias, na época tidas como revolucionárias. Contrariavam praticamente tudo que se acreditava até esse momento no tangente aos movimentos dos planetas em torno do Sol. Teoria essa que também causara furor, no momento de seu lançamento, apesar de as três leis terem sido apresentadas com um espaçamento considerável entre uma e outra. Galileu Galilei foi vítima dessa “revolta” contra as inovações, chegando a ser condenado por heresia. Conta-se que ele teria, para escapar da morte na fogueira da inquisição, jurado publicamente que refutava a teoria de Kepler, tendo porém murmurado em seguida “mas que ela se move, se move”, referindo-se à Terra que até ali era considerada o centro do Universo, fato tido como dogma de fé pela Igreja.
Uma das consequências diretas desse fenômeno gravitacional, é o movimento de queda de um corpo abandonado em um ponto qualquer, acima da superfície da Terra, ou de qualquer outro astro no espaço. Ocorre que os dois corpos se atraem com forças de mesma intensidade, porém, por causa da diferença descomunal de suas massas, o corpo se movimenta em “queda livre”, enquanto o astro permanece na mesma posição. A força adicional é insignificante para alterar sua órbita ou sua rotação.
Analisemos a figura.
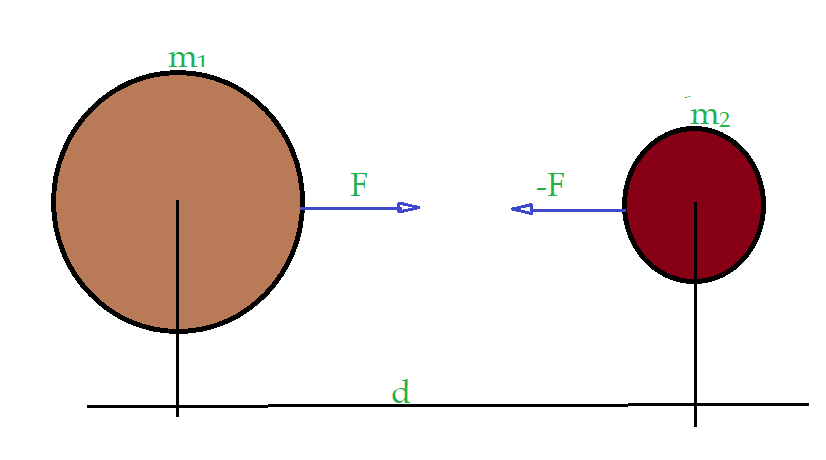
Os dois corpos, que poderiam ser a Terra e a Lua, ou qualquer outro par existente no imenso Universo que nos rodeia. Eles têm massas ${m_1}$ e ${m_2}$, estando seus centros separados pela distância ${d}$. Eles se atraem com forças de mesma direção, mesmo módulo, porém de sentidos opostos, exatamente como preconiza a Terceira Lei de Newton também denominada Lei da atração e repulsão. Aplicando o enunciado da Lei de Gravitação, podemos escrever para qualquer uma das duas forças a expressão:
$$\color{Navy}{F = G\times\left[\frac{(m_1\times m_2)}{d^2}\right]}$$
Quando deixamos cair um corpo de uma determinada altura, salvo quando esta altura alcança algumas dezenas ou mesmo centenas de quilômetros, o valor da força gravitacional que este corpo recebe da Terra é praticamente constante. As pequenas alturas são insignificantes na comparação com o raio do globo terrestre ${R= 6.371 km}$. Por essa razão usamos o valor da aceleração que os corpos sofrem nas proximidades da Terra como aproximadamente constante. Isso é uma aproximação aceitável. Não é algo exato, mas pouco significativa em termos de resultados.
Dessa forma, podemos determinar o valor da aceleração da gravidade ${g}$ pela expressão da Lei de Gravitação. Observe a figura. Estamos representando a massa do corpo em queda pela letra ${m}$ minúscula, destacando que ela é muito pequena em comparação com a Terra. Por sua vez a massa da Terra estamos representando por ${M}$, indicando que é muito maior. Fazendo uso da 2ª Lei de Newton, cuja expressão é dada por ${F = m\times a}$ e substituindo na gravitação teremos.
$$\color{Navy}{F = G\times\left[\frac{M\times m}{d^2}\right]}$$
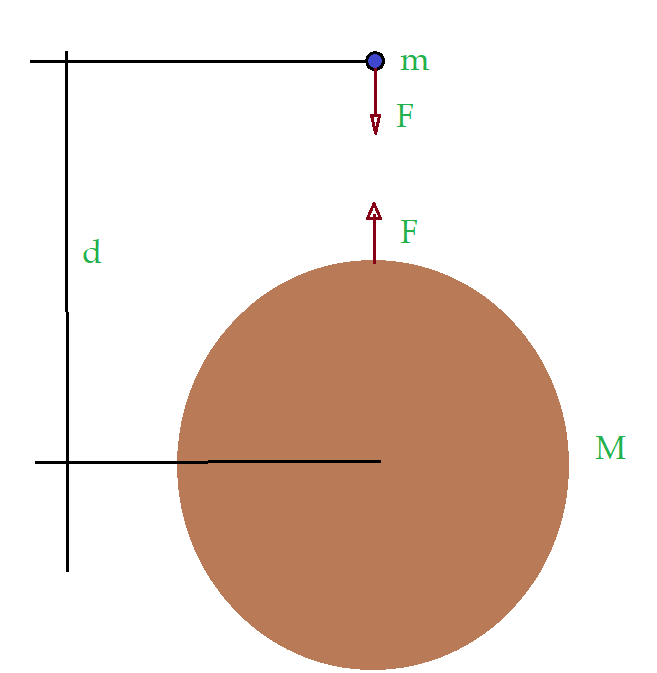
A força de atração da Terra sobre o corpo, é o que em geral denominamos como sendo o peso do corpo.
${F = P = m\times g}$
$\not{m}\times g = G\times\left[\frac{M\times\not{m}}{d^2}\right]$
Substituindo a distância ${d}$ pelo raio da Terra, ficamos com
$$\color{Brown}{g = G\times\frac{M}{R^2}}$$
Nota: A massa da Terra é, em termos aproximados igual a ${m_{T} = {5,9722} × {10}^{24}\,kg}$
| Altitude (km) | Aceleração da Gravidade (m/s^{2}) | Exemplo de altitude |
|---|---|---|
| 0 | 9,83 | nível do mar |
| 8,8 | 9,80 | cume do Monte Everest |
| 36,6 | 9,71 | maior altura atingida por balão tripulado |
| 400 | 8,70 | órbita de um ônibus espacial |
| 35700 | 0,225 | satélite de comunicação |
É hora de praticar um pouco tudo isso.
01. Determine a força de atração entre o Sol e a Terra em termos de 10^{22}\,N sabendo que a massa da Terra é $6.10^{24}\,kg$, a massa do Sol é $2. 10^{30}\,kg$ e a distância entre os dois astros é de $1,5.1^8\,km$.
Sabemos que ${1km = 10^3\,m}$
Temos: $G = 6,67\times 10^{-11}\,N.m^{2}/kg^{2}$
A equação da gravitação é:
$$\color{Maroon}{F = G\times\left[\frac{{m_s}\times {m_t}}{d^{2}}\right]}$$
$F = {6,67}\times {10}^{-11}\times\left[\frac{2\cdot {10}^{30}\times 6\times{10}^{24}}{({1,5}\times{10}^{11})^{2}}\right]$
$F={6,67}\cdot{10}^{-11}\times\left[\frac{{12}\times{10}^{54}}{{2,25}\times{10}^{22}}\right]$
$F = \frac{{80,04}\times{10}^{43}}{{2,25}\times{10}^{22}}$
$F= {35,57}\times{10}^{21}= {3,557}\times{10}^{22}\,N$
$$\color{Maroon}{F = {3,557}\times{10}^{22}\,N}$$
02. (UCB-DF) – A Lei da Gravitação Universal de Newton é expressa por $ F = {G\cdot\frac{M\cdot m}{r^2}}$. Nesta expressão G é a Constante de Gravitação Universal, M é a massa do astro (corpo) maior, m é a massa de um objeto menor. A distância entre os centros de massa dos dois corpos é r e podemos considerar a força com sinal $\pm$, conforme a situação que estejamos analisando. É uma força atrativa. De acordo com essa lei, enunciada por Isaac Newton, se a distância entre um par de corpos é triplicada, a força atrativa entre eles será:
( )a) um nono do valor original;
( )b) um terço do valor original;
( )c) três vezes o valor original;
( )d) nove vezes o valor original;
( )e) o mesmo do valor original.
03. (UFU-MG) – Um dos avanços na compreensão de como a Terra é constituída, deu-se com a obtenção do valor de sua densidade. O primeiro valor foi estabelecido por Henry Cavendisch no século XVIII. Considerando a Terra como uma esfera de raio médio 6.300 km, qual é o valor aproximado de sua massa específica?
Dados: $g = {10}\, m/s^2$ \, $G={6,67}\cdot {10}^{-11} Nm^2/kg^2$ e $\pi = 3$
( )a) ${5,9}\cdot{10}^6\,kg/m^3$;
( )b) ${5,9}\cdot{10}^3\,kg/m^3$;
( )c) ${5,9}\cdot{10}^{24}\,kg/m^3$;
( )d) ${5,9}\cdot{10}^0\,kg/m^3$;
( )e) ${5,9}\cdot{10}^{12}\,kg/m^3$.
04. Considerando a aceleração da gravidade na superfície da Terra como $g = 9,81\,m/s^2$. O raio da Terra tem em média $R = {6,3}\cdot{10}^6\,m$ e a constante de Gravitação vale $G ={6,67}\cdot{10}^{-11}\,Nm^2/kg^2$. Um satélite artificial é lançado e fica estável a uma altura de $h = 3\cdot{10}^4\, m$ acima da superfície da Terra. Qual é, em números aproximados, a aceleração da gravidade na órbita do satélite?
Lei de Gravitação: $F = G\cdot\frac{M\cdot m}{R^2}$
$F = {m\cdot g}$$\Rightarrow$$\not{m}\cdot g = G\cdot\frac{M\cdot\not{m}}{R^2}$
$g = G\cdot\frac{M}{R^2}$ (I)
Para uma órbita de altura $h$, devemos adicionar ao raio da Terra, a altura da órbita.
Assim: $ g_{h}= G\cdot\frac{M}{\left(R + h\right)^2}$ (II)
Dividindo membro a membro as equações (II) e (I)
$$\left(\frac{g_{h}}{g}\right) = \left[\frac{G\cdot M}{\left(R+h\right)^2}\right]\cdot\frac{R^2}{G\cdot M}$$
$$g_{h} = g\cdot\frac{R^2}{\left(R+h\right)^2}$$
$$g_{h} = {9,81}\cdot\frac{\left({6,3}\cdot{10}^6\right)^2}{\left({6,3}\cdot{10}^6 + 3\cdot{10}^4\right)^2}$$
$$\color{maroon}{g_{h}=9,72 m/s^2}$$
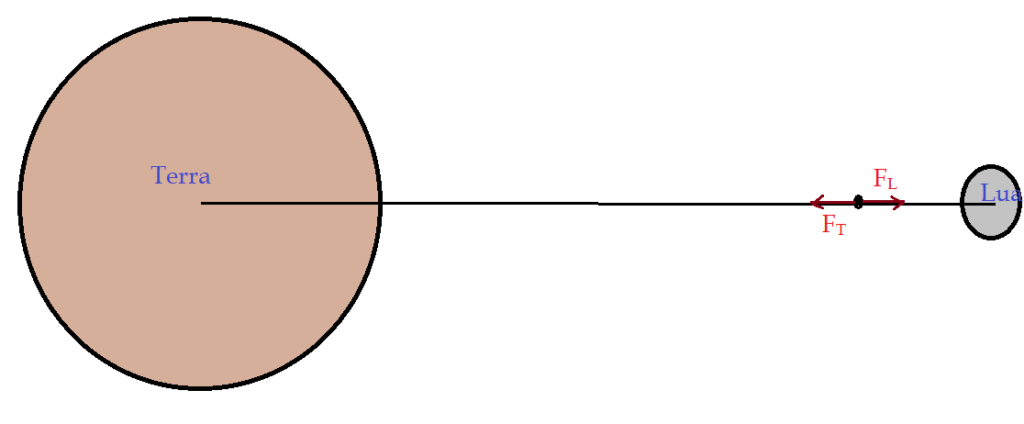
05. Experiências e cálculos demonstraram que a massa da Terra é aproximadamente 80 vezes a massa da Lua. $M_{T} = {81}\cdot M_{L}$ e a aceleração experimentada por um corpo nas proximidades da Lua é aproximadamente igual a um décimo da aceleração gravitacional da Terra. Num dia em que a distância entre os dois astros é de $D_{TL}= 3,87\cdot{10}^8 m$, em que ponto um corpo, colocado sobre a linha que une os centros, ficará sujeito à atrações de mesma intensidade por parte da Terra e da Lua.
Nas condições descritas, o corpo ficaria em equilíbrio, se ali fosse posto desprovido de movimento em qualquer sentido. Podemos então estabelecer a relação:
$$\color{Navy}{F_{T} = F_{L}}$$
Um corpo de massa $m$, fica sob ação de duas forças de mesma intensidade e sentidos opostos, exercidas pela Terra e a Lua respectivamente.
$$G\cdot\frac{M_{T}\cdot m}{\left(R_{T}\right)^2} = G\cdot\frac{M_{L}\cdot m}{\left(R_{L}\right)^2}$$
Cancelando os fatores comuns dos dois membros:
$$\frac{M_{T}}{\left(R_{T}\right)^2} = \frac{M_{L}}{\left(R_{L}\right)^2}$$
Substituindo $M_{T} = {81}\cdot M_{L}$
$$\frac{{81}\cdot M_{L}}{\left(R_{T}\right)^2}= \frac{M_{L}}{\left(R_{L}\right)^2}$$
Cancelando fator comum $M_{L}$
$$\frac{81}{R_{T}^2} = \frac{1}{R_{L}^2}$$
Sabemos que $R_{T} + R_{L} = 3,87\cdot {10}^8 m$, onde podemos retirar:
$R_{T} = {3,87}\cdot{10}^8 – R_{L}$ (I)
$$\sqrt{\frac{81}{R_{T}^2}} = \sqrt{\frac{1}{R_{L}^2}}$$
$$\frac{9}{R_{T}} = \frac{1}{R_{L}}$$ (II)
Substituindo (I) em (II), temos:
$$ \frac{9}{{3,87}\cdot{10}^8 – R_{L}} = \frac{1}{R_{L}}$$
$$ 9\cdot R_{L} = {3,87}\cdot{10}^8 – R_{L}$$
$$9\cdot R_{L} + R_{L} = {3,87}\cdot{10}^8 $$
$${10}\cdot R_{L} = {3,87}\cdot {10}^8$$
$$ R_{L} = \frac{{3,87}\cdot{10}^8}{10}$$
$$ R_{L} = {3,87}\cdot{10}^7 m$$
A distância em que o corpo ficará em equilíbrio corresponde a $\frac{1}{10}$ da distância entre a Terra e a Lua no momento. Se medir em relação à Terra, teremos como resposta um valor correspondente à $\frac{9}{10}$ da mesma distância.
Para treinar por conta.
01. (UFRS) – O módulo da força de atração gravitacional entre duas pequenas esferas de massas $m$, cujos centros estão separados por uma distância $d$ é $F$. Substituindo uma das esferas por outra de massa $2m$ e reduzindo a separação entre os centros das esferas para $\frac{d}{2}$, resulta uma força gravitacional de módulo igual a?
02. A força de atração gravitacional entre dois corpos de massas m_{1} e m_{2}, tem módulo $F=G\cdot\frac{m_{1}\cdot m_{2}}{r^2}$, em que $r$ é a distância entre eles e $G ={6,7}\cdot{10}^{-11}\,Nm^2/kg^2$, é a Constante Universal de Gravitação. Sabendo que a massa de Júpiter é $m_{J}= 2,0\cdot{10}^{27}\,kg$ e que a massa da Terra é $m_{T}=6,0\cdot{10}^{24}\, kg$, o módulo da força gravitacional entre Júpiter e a Terra, no momento de maior proximidade $r_{mínima}=6\cdot{10}^{11}\,m$, é:
( )a) $1,4\cdot{10}^8\,N$;
( )b) $2,2\cdot{10}^{18}\,N$;
( )c) $3,5\cdot{10}^{19}\,N$;
( )d) $1,3\cdot{10}^{30}\,N$;
( )e) $2,7\cdot{10}^{25}\,N$.
03. Dois objetos de massas $M$ e $m$, estão separados por uma distância $r$ no espaço. Eles se atraem com uma força de intensidade $F$. Se a massa $M$ for multiplicada por $2$ e a distância $r$ for quadruplicada, qual será o módulo da nova força de atração $F’$?
( )a) $\frac{1}{2}\cdot F$;
( )b) $\frac{1}{8}\cdot F$;
( )c) $2\cdot F$;
( )d) $F$;
( )e) $\frac{1}{3}\cdot F$.
04. Marque com um (X) a afirmativa correta relativamente à Lei de Gravitação Universal:
( )a) A equação da Lei de Gravitação Universal prevê tanto uma força de atração como uma de repulsão;
( )b) Se a distância entre dois objetos for triplicada, a força gravitacional entre eles será seis vezes menor;
( )c) Se as massas dos planetas do sistema solar sofressem variações consideráveis, nada mudaria, pois a força gravitacional depende apenas da massa do Sol;
( )d) A força gravitacional é diretamente proporcional ao quadrado da distância que separa dois corpos;
( )e) A força de atração gravitacional é inversamente proporcional ao quadrado da distância que separa os dois corpos.
05. A força de atração gravitacional entre dois objetos de massas $m_{1} = 50,0\,kg $ e $m_{2} =100,0\,kg$, é de $ 13,4\,N$. Determine a distância aproximada que separa esses dois objetos. Não esquecer que $G = {6,67}\cdot{10}^{-11}\ Nm^2/kg^2$.
( )a) $2,5\cdot {10}^{-4}\,m$;
( )b) $2,05\cdot{10}^{-4}\,m$;
( )c) $1,4\cdot{10}^{-4}\,m$;
( )d) $1,20\cdot{10}^{-4}\,m$;
( )e) $1,60\cdot{10}^{-4}\,m$.
06. A Estação Espacial Internacional orbita a Terra em uma altitude h. A aceleração da gravidade terrestre dentro dessa espaçonave é:
Obs.: Considere $g_{T}$$\rightarrow$ aceleração da gravidade na superfície da Terra.
$r_{T}$$\rightarrow$ raio da Terra na superfície.
( )a) nula;
( )b) $g_{T}\cdot\left(\frac{h}{R_{T}}\right)^2$;
( )c) $g_{T}\cdot\left(\frac{R_{T} – h}{R_{T}}\right)^2$;
( )d) $g_{T}\cdot\left(\frac{R_{T}}{R_{T}+h}\right)^2$;
( )e)$g_{T}\cdot\left(\frac{R_{T} – h}{R_{T} +h}\right)^2$
07. Um satélite artificial descreve uma órbita circular em torno da Terra com período $T = 4\pi\sqrt{\frac{2R}{g}}$ , em que R é o raio da Terra e g a aceleração da gravidade na superfície terrestre. A que altura x, acima da superfície, se encontra o satélite?
08. Um satélite, em órbita circular em torno da Lua, tem período nove vezes maior que o de um satélite em órbita circular de mesmo raio em torno da Terra. Conclui-se que o valor da razão entre a massa da Terra e a massa da Lua é igual a:
( )a) 3;
( )b) 9;
( )c) 27;
( )d) 81;
( )e) 243.
09. A Terra gira em torno do Sol numa órbita que pode ser considerada circular, com a velocidade angular aproximadamente constante. Mantendo fixo o raio dessa órbita, mas imaginando que a massa do Sol fosse quatro vezes maior do que realmente é, a velocidade angular do movimento de translação da Terra seria:
( ) a) duas vezes maior;
( )b) quatro vezes maior;
( )c) a mesma;
( )d) a metade;
( )e) nenhuma das anteriores.
10. Dois satélites, 1 e 2, giram em torno da Terra em órbitas circulares idênticas, sendo que $m_{1}\gt m_{2}$. Pode-se afirmar que:
( )a) a velocidade escalar de 1 é maior que a de 2;
( )b) o período de 1 é maior que o de 2
( )c) a força de atração entre a Terra e os satélites 1 e 2 tem mesma intensidade;
( )d) as acelerações de 1 e 2 são diferentes;
( )e) as velocidades e os períodos de 1 e 2 são respectivamente iguais.
11. A massa da Terra é, aproximadamente, 81 vezes a massa da Lua. O raio da Terra é R e a distância do centro da Terra ao centro da Lua é de aproximadamente 60 R. A distância do centro da Terra em que o campo gravitacional dos astros Terra e Lua se anulam, em raios terrestres, vale:
( )a) 60R;
( )b) 54 R;
( )c) 45 R;
( )d) 30 R;
( )e) 6 R.
12. Que alteração sofreria o módulo da aceleração da gravidade se a massa da Terra fosse reduzida à metade e o seu raio diminuído de 1/4 de seu valor real?
13. Suponha que a Terra tivesse uma aceleração da gravidade com valor igual à metade do atual e que seu raio também tivesse a metade do seu valor atual. Se M é a massa atual da Terra, qual seria a massa desta Terra hipotética?
14. Um homem na Terra pesa ${1,00}\cdot{10}^3\,N$. Qual o seu peso em Júpiter sabendo-se que, comparado com a Terra, esse planeta tem massa $320$ vezes maior e raio $11$ vezes maior?
15. Qual é a força de atração gravitacional entre duas massas de $100\,kg$ cada uma, distantes 1 metro uma da outra? (Considere $G = {6,7}\cdot{10}^{–11}\,Nm^2 /kg^2$.
( )a) 104\,N;
( )b) 102\,N;
( )c) 6,7\,N;
( )d) 6,7 · 10–9\,N;
( )e) 6,7 · 10–7\,N.
16. Calcule a força de atração gravitacional entre duas massas de 500 kg distantes 5 m uma da outra. Use $G=6,67\times{10}^{-11}\,Nm^{2}/kg^{2}$.
17. (PUC-SP) – A intensidade da força gravitacional com que a Terra atrai a Lua é F. Se fossem duplicadas a massa da Terra e da Lua e se a distância que as separa fosse reduzida à metade, a nova força seria:
( )a) 16F;
( )b) 8F;
( )c) 4F;
( )d) 2F;
( )e) F.
18. O gráfico a seguir mostra que dois corpos atraem-se com força gravitacional que varia com a distância entre seus centros de massa. Calcule o valor de F assinalado no gráfico.
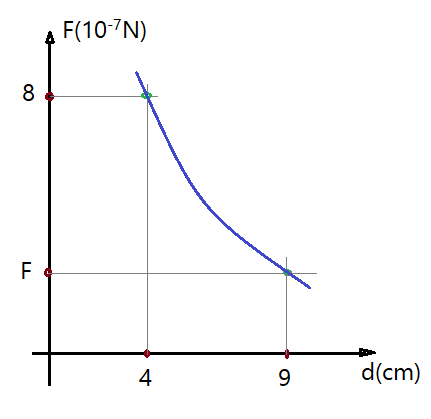
Gráfico demonstrando a força gravitacional entre dois corpos em função da distância.
19, (CESGRANRIO) – A força da atração gravitacional entre dois corpos celestes é proporcional ao inverso do quadrado da distância entre os dois corpos. Assim, quando a distância entre um cometa e o Sol diminui da metade, a força de atração exercida pelo Sol sobre o cometa:
( )a) diminui da metade;
( )b) é multiplicada por 2;
( )c) é dividida por 4;
( )d) é multiplicada por 4;
( )e) permanece constante.
20. Considere que os centros de massa de duas pessoas adultas estão separados pela distância de $d= 2,0\,m$ e que suas massas são aproximadamente iguais a $m_{1} = m_{2}=100\,kg$. A intensidade da força de atração gravitacional entre elas é um valor mais próximo de?
Dado: constante da gravitação universal $G = 6,7\times 10^{-11}\,Nm^{2}/kg^{2}$.
( )a) $1,7\times 10^{-7}\,N$;
( )b) $3,4 \times 10^{-7}\,N$;
( )c) $1,7 \times 10^{-7}\,N$;
( )d) $3,4 \times 10^{-7}\,N$;
( )e) $1,7 \times 10^{-6}\,N$.
21. Considere um corpo A de massa $m_{A}= 20\,kg$. Para que este corpo atraia o planeta Terra com uma força de $F=50\,N$, sua distância à superfície terrestre deve ser aproximadamente igual:
( )a) ao raio da Terra;
( )b) ao dobro do raio da Terra;
( )c) ao quádruplo do raio da Terra;
( )d) à metade do raio da Terra;
( )e) a um quarto do raio da Terra.
22. Em certo sistema planetário, alinham-se, em um dado momento, um planeta, um asteroide e um satélite, como representa a figura.

Sabe-se que:
(1) A massa do satélite é mil vezes menor do que a massa do planeta;
(2) o raio do satélite é muito menor do que o raio R do planeta.
Calcule a razão entre as forças gravitacionais exercidas pelo planeta e pelo satélite sobre o asteroide.
Se ficar com dúvidas, ou tiver outros exercícios, provenientes de cursos, apostilas que não consiga resolver, peça ajuda que estou aqui para isso. Disponha.
Curitiba, 01 de fevereiro de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
