Física – Ótica Lentes esféricas
Equação dos pontos conjugados.
Eu poderia simplesmente dizer que a equação dos pontos conjugados para as lentes tem a mesma forma que usamos nos espelhos esféricos. Mas isso não explica por que é assim, apesar de ser verdade. Vamos fazer a demonstração para que você saiba que ela não existe por mero acaso, ou por obra e graça de um iluminado que recebeu essa revelação. Há uma lógica na sua obtenção. Sabendo de onde ela vem, torna mais fácil aplicar e entender os resultados.
Observemos a figura.
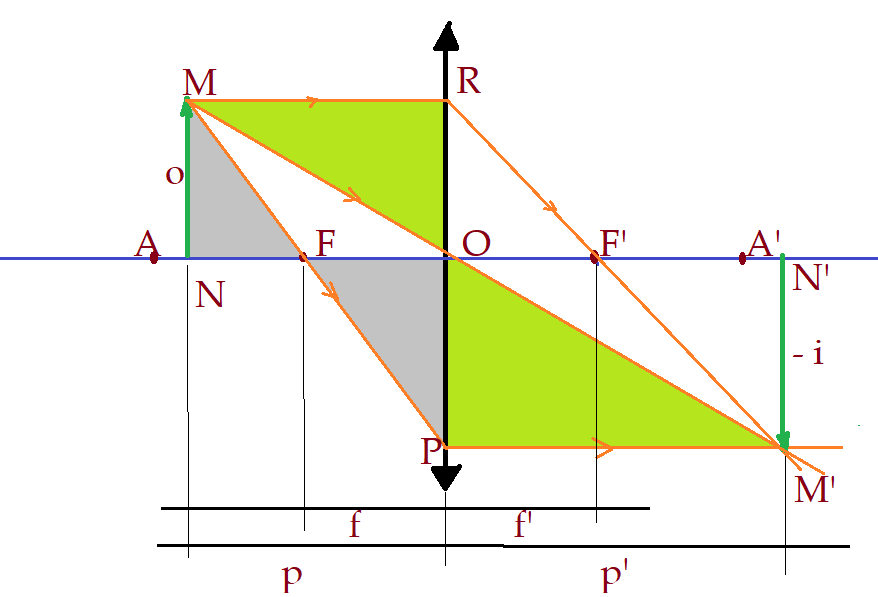
Observemos os triângulos $\Delta{NMFN}$e o $\Delta{OSFO}$.Eles tem um ângulo reto e um dos ângulos agudos de cada um é oposto pelo vértice $\hat{F}$ ao outro. São pois triângulos semelhantes e seus lados homólogos são proporcionais:
${\overline{NM}\over\overline{NF}}={\overline{OP}\over\overline{OF}}$
Olhando a figura vemos que:
$\overline{NM}= o$
$\overline{OP} = \overline{N’M’} = -i $
$\overline{OF}= f $
$\overline{NF} = p – f $
Substituindo na relação acima, teremos:
${{-i}\over f}= {o\over{p – f}}$$\Leftrightarrow$$ -{i\over f}= {o\over{p – f}}$
Alternando os “meios” da razão, fica:
$ -{i\over o} = {f\over{p-f}}$ (I)
Observando os triângulos $\Delta{MROM}$ e $\Delta{M’POM’}$, vemos que também são semelhantes e seus lados proporcionais.
${\overline{PO}\over\overline{OR}} = {\overline{PM’}\over\overline{RM}}$
$ – {i\over o} = {p’\over p}$ (II)
Igualando as duas ou substituindo (II) em (I):
${p’\over p} = {f\over{p – f}}$$\Leftrightarrow$${p’\cdot{(p – f)}} ={p\cdot f}$
${p\cdot p’ – p’\cdot f} = {p\cdot f}$
Multiplicando a expressão inteira por ${1\over{p\cdot p’\cdot f}}$, teremos:
${{p\cdot p’}\over{p\cdot p’\cdot f}}-{{p’\cdot f}\over{p\cdot p’\cdot f}}={{p\cdot f}\over{p\cdot p’\cdot f}}$$\Leftrightarrow$${1\over f} – {1\over p} = {1\over p’}$
Reordenando os termos:
${1\over f} = {1\over p} + {1\over p’}$
A razão entre $-{i\over o}$, nos fornece a ampliação linear da imagem em relação ao objeto e podemos escrever a equação dos pontos conjugados.
$A = {i\over o} = – {p’\over p}$
Hora de exercitar
01. Uma lente convergente, cuja distância focal mede $f = 20,0 cm$, tem colocada diante dela um objeto real de $o = 5,0 cm$, situado à uma distância de $p = 30,0 cm$. Determinar: a) a posição da imagem em relação à lente; b) a natureza da imagem; c) o tamanho da imagem e a ampliação linear.
a) $f = 20,0 cm$
$p = 30,0 cm$.
$$\color{Maroon}{\frac{1}{f} = \frac{1}{p} + \frac{1}{p’}}$$
Substituímos:
${1\over {20,0}} = {1\over {30,0}} + {1\over p’}$$\Leftrightarrow$${1\over {20,0}} – {1\over{30,0}}= {1\over p’}$
O mmc(20,0 e 30,0) = 60,0.
${{3 – 2}\over{60,0}} = {1\over p’}$$\Leftrightarrow$$p’ = 60,0 cm$
b) Como a distância da lente à imagem deu positiva, a imagem é real.
c) $O = 5,0 cm$
${I\over O} = – {p’\over p}$
${I\over{5,0}} = -{{60,0}\over {20,0}}$${i\over {5,0} = – 3$
$I = -15,0\,cm$
$A = – {p’\over p}$$\Leftrightarrow$$A =-{{75,0}\over{25,0}$
$A = – 3$
Imagem invertida e com o triplo do tamanho do objeto.
02. Se uma lente fornece imagem virtual de $i = 48,0 cm$ para um objeto de $o = 12,0 cm$, colocado à uma distância $p = 25,0 cm$, determine: a) a posição da imagem e a distância focal da lente; b) a ampliação da imagem e sua posição com relação ao objeto; c) a natureza da lente.
a) $I = 48,0\,cm$; $O = 12,0\,cm$ e $p = 25,0\,cm$.
$A = {i\over o} = – {p’\over p}$ e ${1\over f} = {1\over p} + {1\over p’}$
Substituindo: $ {i\over o} = – {p’\over p}$
$ – {{48,0}\over {12,0}} = {p’\over {25,0}}$ $\Leftrightarrow$$- {3\cdot{25,0}} = p’$
$p’ = – 75,00 cm$
A imagem encontra-se a $p’ = -75,0 cm$, antes da lente. Não esqueçamos que ela é virtual.
${1\over f} = {1\over {25,0}} – {1\over {75,0}}$
${1\over f} = {{3 – 1}\over {75,0}}$$\Leftrightarrow$${1\over f} = {2\over {75,0}}$
$ f = {{75,0}\over 2} = 37,5 cm$
b)$A = {i\over o} = – {p’\over p}$
$A = – {-{75,0}\over {25,0}} = 3$
c)a lente é convergente, sua distância focal é positiva.
03. Uma lente divergente, tem distância focal $f = – 10,0 cm$. Coloca-se diante dela um objeto de $o = 8,0 cm$, à $p = 40,0 cm$. Pergunta-se: a) podemos projetar a imagem em um anteparo? b) qual é a posição em que se formará a imagem? c) qual é a ampliação da imagem e suas características em relação ao objeto.
a)Dados: $f = -10,0 cm$; $o = 8,0 cm$ e $p = 40,0 cm$
Sendo lente divergente, a projeção de imagens é inviável, uma vez que ela só fornece imagens virtuais.
b)${1\over f} = {1\over p} + {1\over p’}$$\Leftrightarrow$${1\over{-{10,0}}} = {1\over {40,0}} + {1\over p’}$
$ – {1\over {10,0}} – {1\over {40,0}} = {1\over p’}$$\Leftrightarrow$${{- 4 – 1}\over{40,0}} = {1\over p’}$
${-5\over {40,0}} = {1\over p’}$$\Leftrightarrow$${1\over p’} = – {1\over {8,0}}$
$p’ = – 8,0 cm$
04. Uma lente conjuga uma imagem real a um objeto de $o = 16,0 cm$, que se situa a uma distância $p = 60,0 cm$. A imagem forma-se à $p’ = 30,0 cm$. Determine: a) a distância focal da lente e sua natureza; b) a natureza da imagem e seu tamanho.
Dados: $p = 60,0 cm$; $o = 16,0 cm$ e $p’ = 30,0 cm$
a)${1\over f} = {1\over p} + {1\over p’}$
${1\over f} = {1\over {60,0}} + {1\over {30,0}}$$\Leftrightarrow$${1\over f}={{1 + 2}\over{60,0}}$
${1\over f} = {3\over{60,0}}$$\Leftrightarrow$${1\over f} = {1\over{20,0}}$
$f = 20,0 cm$$\Leftrightarrow$ lente convergente, tem distância focal $f\gt 0$
b) Como $p’ \gt 0$, a imagem é real.
Sendo $A = -{p’\over p}$$\Leftrightarrow$$ A = – {{30,0}\over{60,0}}$
$A = -{1\over 2}$$\rightarrow$ imagem invertida e menor que o objeto.
Pratique você
01. Suponhamos que um objeto é colocado a $p = 60 cm$ de uma lente esférica do tipo convergente. Tal lente possui distância focal igual a $f = 20 cm$. Calcule a distância da imagem à lente, a ampliação linear da imagem em relação ao objeto e a natureza da imagem.
02. (ITA-SP) Um objeto tem altura H = 20 cm e está situado a uma distância p = 30 cm de uma lente. Esse objeto produz uma imagem virtual de altura h = 4,0 cm. A distância da imagem à lente, a distância focal e o tipo de lente são, respectivamente:
( )a) 6,0 cm; 7,5 cm; convergente;
( )b) 1,7 cm; 30 cm; divergente;
( )c) 6,0 cm; –7,5 cm; divergente;
( )d) 6,0 cm; 5,0 cm; divergente;
( )e) 1,7 cm; –5,0 cm; convergente.
03. (Fuvest-SP) A distância entre um objeto e uma tela é de 80 cm. O objeto é iluminado e, por meio de uma lente delgada posicionada adequadamente entre o objeto e a tela, uma imagem do objeto, nítida e ampliada três vezes, é obtida sobre a tela. Para que isto seja possível, a lente deve ser: ( )a) convergente, com distância focal de 15 cm, colocada a 20 cm do objeto; ( )b) convergente, com distância focal de 20 cm, colocada a 20 cm do objeto; ( )c) convergente, com distância focal de 15 cm, colocada a 60 cm do objeto; ( )d) divergente, com distância focal de 15 cm, colocada a 60 cm do objeto; ( )e) divergente, com distância focal de 20 cm, colocada a 20 cm do objeto;
04. Mediante o uso de uma lente delgada, um estudante acende uma chama numa folha de papel situada a 20 cm da lente, aproveitando a luz solar. Qual a distância focal da lente?
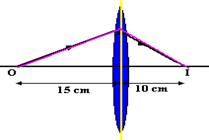
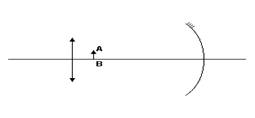
05. – (UNIESP-SP) – Na figura estão representados esquematicamente o perfil de uma lente esférica, de vidro, imersa no ar e a trajetória de um raio de luz que parte do ponto O no eixo principal, incide na lente e emerge passando novamente pelo mesmo eixo, no ponto I.
a) A lente da figura é convergente ou divergente? Justifique sua resposta.
b) Admitindo-se válidas as condições de astigmatismo de Gauss, calcule a distância foca dessa lente.
06. (UTF_RJ) – Um operador cinematográfico deve saber selecionar a lente de projeção adequada para que a tela fique totalmente preenchida com a imagem do filme. A largura de um quadro na fita de um filme de longa metragem é 35 mm. Para um cinema em que a tela tem 10,5 m de largura e está a 30 m da lente da máquina de projeção, determine: a) a ampliação necessária para que a tela seja totalmente utilizada; b) a distância entre a fita e a lente para que a ampliação necessária seja obtida;
c) e a distância focal da lente.
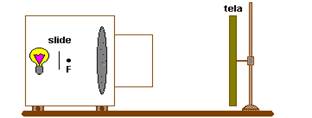
07. (UNESP-SP) – Um projetor rudimentar, confeccionado com uma lente convergente, tem o objetivo de formar uma imagem real e aumentada de um slide. Quando esse slide é colocado bem próximo do foco da lente e fortemente iluminado, produz-se uma imagem real, que pode ser projetada em uma tela, como ilustrado na figura. A distância focal é $f = 5,0 cm$ e é colocado a $p = 6,0 cm$ da lente. A imagem projetada é real e direita. Calcule:
a) a posição, em relação à lente, onde se deve colocar a tela, para se ter uma boa imagem;
b) a ampliação lateral (aumento linear transversal).
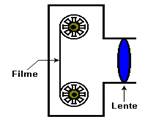
08. (UNESP-SP) – Uma câmara fotográfica rudimentar utiliza uma lente convergente de distância focal $f = 50 mm$ para focalizar e projetar a imagem de um objeto sobre o filme. A distância da lente ao filme é $p’= 52 mm$. A figura mostra o esboço dessa câmara. Para se obter uma boa foto é necessário que a imagem do objeto seja formada exatamente sobre o filme e o seu tamanho não deve exceder a área sensível do filme. Assim: a) Calcule a posição que o objeto deve ficar em relação ao filme. b) Sabendo-se que a altura máxima da imagem não pode exceder a 36,0 mm, determine a altura máxima do objeto para que ele seja fotografado em toda sua extensão.
09. (UNIFESP-SP) – Uma lente convergente tem uma distância focal $f = 20,0 cm$ quando o meio ambiente onde ela é utilizada é o ar. Ao colocarmos um objeto a uma distância $p= 40,0 cm$ da lente uma imagem real e de mesmo tamanho que o objeto é formada a uma distância $p’= 40,0 cm$ da lente. Quando essa lente passa a ser utilizada na água, sua distância focal é modificada e passa a ser $f_{1}=65,0 cm$. Se mantivermos o mesmo objeto à mesma distância da lente, agora no meio aquoso, é correto afirmar que a imagem será:
( )a) virtual, direita e maior;
( )b) virtual, invertida e maior;
( )c) real, direita e maior;
( )d) real, invertida e menor;
( )e) real, direita e menor.
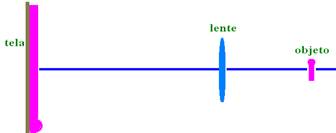
10. (UNESP-SP) – Dispõem-se de uma tela, de um objeto e de uma lente convergente com distância focal $f = 12,0 cm$. Pretende-se, com auxílio dessa lente, obter na tela uma imagem desse objeto cujo tamanho seja 4 vezes maior que o objeto. a) A que distância da lente deverá ficar a tela? b) A que distância da lente deverá ficar o objeto?
11. (UEM) – Um objeto de tamanho igual a $o = 15,0 cm$ está situado a uma distância igual a $p = 30,0 cm$ de uma lente. Verifica-se que a lente forma uma imagem virtual do objeto cujo tamanho é igual $i = 3,0 cm$. Qual é o módulo da distância (em cm) da imagem à lente?
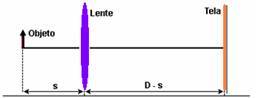
12. (UFPE) – Um objeto luminoso e uma tela de projeção estão separados pela distância $D = 80,0 cm$. Existem duas posições em que uma lente convergente de distância focal $f=15,0 cm$, colocada entre o objeto e a tela, produz uma imagem real na tela. Calcule a distância, em cm, entre estas duas posições.
13. (UNESP-SP) – Uma pessoa, com certa deficiência visual, utiliza óculos com lentes convergentes. Colocando-se um objeto de 0,6 cm de altura a $p = 25,0 cm$ da lente, é obtida uma imagem a $p’=100,0 cm$ da lente. Considerando que a imagem e o objeto estão localizados do mesmo lado da lente, calcule:
a) a convergência da lente, em dioptrias.
b) a altura da imagem do objeto formada pela lente.
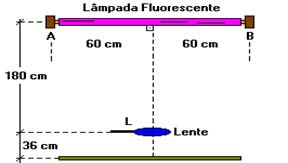
14. (FUVEST-SP) – Uma lente L é colocada sob uma lâmpada fluorescente $\overline{AB}$ cujo comprimento é $\overline{AB} = 120,0 cm$. A imagem é focalizada na superfície de uma mesa a $p’=36,0 cm$ da lente. A lente situa-se a $p = 180,0 cm$ da lâmpada e o seu eixo principal é perpendicular à face cilíndrica da lâmpada e à superfície plana da mesa. A figura a seguir ilustra a situação. Pede-se:
a) a distância focal da lente.
b) o comprimento da imagem da lâmpada e a sua representação geométrica. Utiliza os símbolos A’ e B’ para indicar as extremidades da imagem da lâmpada.
15. (UFU-MG) – Um objeto $O$ de 1,0 cm de altura é colocado a uma distância $d = 2,0 cm$ do foco de uma lente convergente $L_{1}$ de distância focal $f = 1,5 cm$, conforme figura a seguir. Deseja-se aumentar a imagem formada por este objeto, de modo que ela atinja 6 vezes a altura objeto original. Para isso utiliza-se uma segunda lente $L_{2}$, de características idênticas à $L_{1}$.
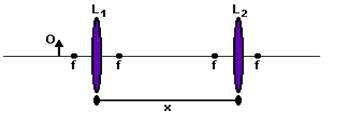
Calcule a que distância x essa segunda lente $L_{2}$, deve ser colocada da lente $L_{1}$ para que a imagem formada seja real, direita e 6 vezes maior que o objeto original.
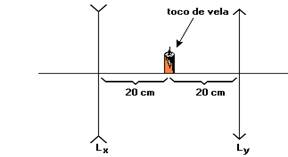
16. (PUC-SP) – Um toco de vela está entre duas lentes delgadas, uma divergente $L_{x}$ e outra convergente $L_{v}$, a 20 cm de cada uma, como está representado no esquema a seguir. As duas lentes tem distâncias focais de mesmo valor absoluto, 10 cm. Nessas condições, a distância entre as imagens do toco de vela, conjugadas pelas lentes vale, em cm, aproximadamente:
( )a) 6,6;
( )b) 20;
( )c) 33;
( )d) 47;
( )e) 53.
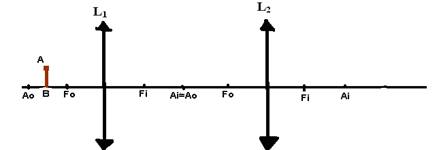
17. (UFB) – Considere duas lentes convergentes $L_{1}$ e $L_{2}$ de mesmo ponto antiprincipal, com eixos principais coincidentes e dispostas de modo que o ponto antiprincipal imagem de $L_{1}$ coincida com o ponto antiprincipal objeto de $L_{2}$. Um objeto $\overline{AB}$ é colocado antes de $L_{1}$ entre $A_{o}$ e $F_{o}$. Determine as características da imagem final formada pelo sistema de lentes.
18. (PUC_SP) – Um espelho côncavo de distância focal $f_{e} = 30,0 cm$ e uma lente convergente de distância focal $f_{l} =12,0 cm$ são dispostos coaxialmente, separados por uma distância de $D=75,0 cm$. Um objeto $\overline{AB}$ é colocado entre o espelho e a lente, a 15,0 cm da lente. Admitindo que o espelho e a lente estão sendo usados dentro das condições de Gauss, a imagem obtida por reflexão no espelho e refração na lente, é: ( )a) real, direita e a 60,0 cm da lente;
( )b) virtual, direita e a 60,0 cm da lente;
( )c) real, invertida e a 30,0 cm da lente;
( )d) real, direita e a 30,0 cm da lente;
( )e) real, invertida e a 15,0 cm da lente.
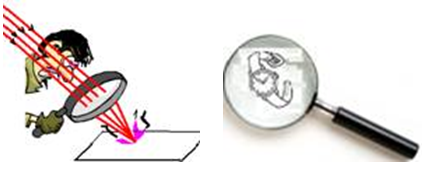
19. (UFPR_PR) – Um estudante usando uma lupa sob a luz do sol consegue queimar uma folha de papel devido à concentração dos raios do sol em uma pequena região. Ele verificou que a maior concentração dos raios solares ocorria quando a distância entre o papel e a lente era de 20,0 cm. com a mesma lupa, ele observou letras em seu relógio e constatou que uma imagem nítida delas era obtida quando a lente e o relógio estavam separados por uma distância de 10,0 cm. A partir dessas informações, considere as seguintes afirmativas: 1. A distância focal da lente vale $f= 20,0 cm$; 2. A imagem das letras formada pela lente é invertida e virtual; 3. A lente produz uma imagem cujo tamanho é duas vezes maior que o tamanho das letras impressas no relógio;
Assinale a alternativa correta. ( )a) somente a afirmativa 1 é verdadeira; ( )b) somente a afirmativa 2 é verdadeira; ( )c) somente a afirmativa 3 é verdadeira; ( )d) somente as afirmativas 1 e 3 são verdadeiras; ( )e) somente as afirmativas 2 e 3 são verdadeiras.
Havendo dúvidas, consulte por meio de um dos canais listados abaixo. Não há por que ficar sem saber tudo detalhadamente.
Curitiba, 07 de dezembro de 2019.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
