Física – Ótica geométrica. Equação de Halley
Equação dos dioptros esféricos
Até o momento aplicamos as leis da refração em superfícies planas, ou seja trabalhamos apenas com dioptros planos. Chegou o momento de aprendermos a usar os dioptros esféricos, que nos permitirão deduzir a equação dos fabricantes de lentes, desenvolvida por Edmond Halley. Pensou no cometa? Pois pensou certo. Foi esse contemporaneo de Isaac Newton que calculou o período do cometa batizado com seu nome, que aparece a cada 76 anos para nos fazer uma visita de alguns dias e depois segue percorrendo sua trajetória.
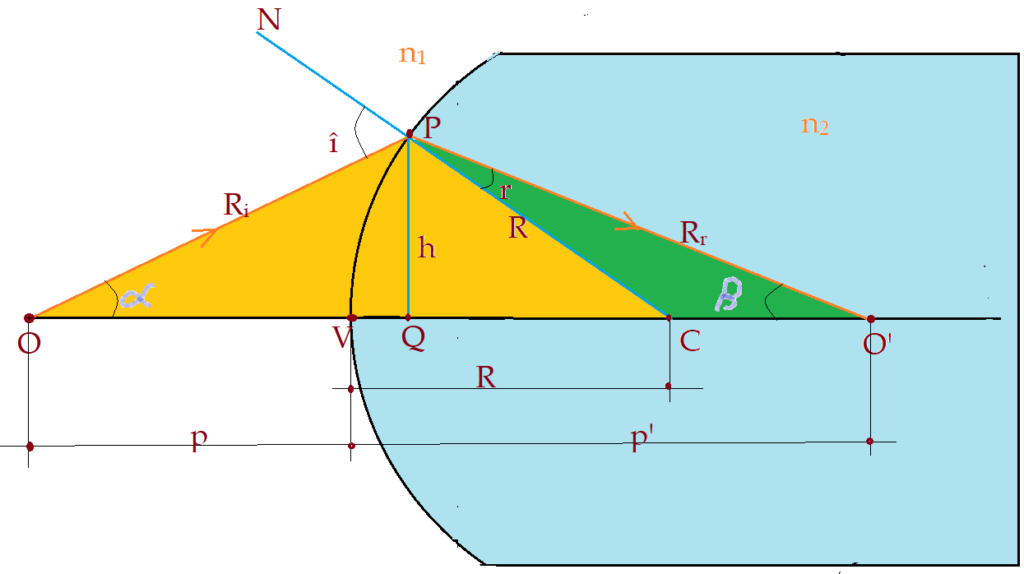
Vejamos a figura a seguir.
No desenho está representada a trajetória de um raio luminoso emitido pelo objeto $\color{Maroon}{O}$, incidindo no ponto $\color{Maroon}{P}$ formando o ângulo $\color{Maroon}{\hat{i}}$ com a normal, prolongamento do raio $\color{Maroon}{R}$. Ele se refrata num ângulo $\hat{r}$, interceptando o raio incidente no vértice e se refrata sem desvio, no ponto $\color{Maroon}{O’}$. O raio $\color{Maroon}{\widehat{OV}}$ incide na direção normal, pois coincide com o raio de curvatura.
Para os ângulos $\color{Maroon}{\hat{i}}$ e $\color{Maroon}{\hat{r}}$, vale a relação:
$$\color{Brown}{sen(\hat{i})\times n_{1} = sen(\hat{r})\times n_{2}}$$
Nos triângulos $\color{Maroon}{\Delta{PCOP}}$ e $\color{Maroon}{\Delta{PCO’P}}$, vale a lei dos senos, visto no estudo de trigonometria em matemática.
$\left(\frac{p + R}{sen(\hat{i})}\right) =\left(\frac{R}{sen\alpha}\right)$ (I)
$\left(\frac{p’ – R}{sen (\hat{r})}\right) = \left(\frac{R}{sen\beta}\right)$ (II)
Dividindo membro a membro as equações (I) e (II), teremos:
$\left[\frac{\left(\frac{p + R}{sen(\hat{i})}\right)}{\left(\frac{p’ – R}{sen (\hat{r})}\right)}\right] = \left[\frac{\left(\frac{R}{sen\alpha}\right)}{\left(\frac{R}{sen\beta}\right)}\right]$$\Leftrightarrow$$ \left[{\left(\frac{p + R}{sen(\hat{i})}\right)\times \left(\frac{sen(\hat{r})}{p’ – R}\right)}\right] = \left[{\left(\frac{\not {R}}{sen\alpha}\right)\times\left(\frac{sen\beta}{\not{ R}}\right)}\right] $
$\left({p + R}\right)\times\left(\frac{sen\alpha}{sen(\hat{i})}\right)= \left({p’ – R}\right)\times\left(\frac{sen\beta}{sen(\hat{r})}\right)$ (III)
Que pode ser reescrita assim:
$\left({p + R}\right)\times\left(\frac{sen\alpha}{sen\beta}\right) = \left({p’ – R}\right)\times\left(\frac{sen(\hat{i})}{sen(\hat{r})}\right)$ (IV)
Como precisamos usar as condições de nitidez, ou astigmatismo de Gauss, os ângulos $\alpha$ e $\beta$, são muito pequenos, se aproximando de $\color{Maroon}{0}$, temos que $\color{Maroon}{\alpha\simeq sen\alpha\simeq tg\alpha}$. O mesmo vale para $\color{Maroon}{\beta}$.
Então, observando na figura de lente delgada, os triângulos $\color{Maroon}{\Delta{PQOP}}$ e $\color{Maroon}{\Delta{PQO’P}}$ teremos:
$\color{Navy}{tg\alpha\simeq \frac{h}{p}}$ (V)
$\color{Blue}{tg\beta\simeq\frac{h}{p’}}$ (VI)
Como sabemos: $\color{Maroon}{\frac{sen(\hat{i})}{sen(\hat{r})} = \frac{n_{2}}{n_{1}}}$ (VII)
Podemos escrever: $\color{Brown}{\frac{sen\alpha}{sen\beta}\simeq\frac{tg\alpha}{tg\beta}}$ (VIII)
Temos então: $\left(\frac{tg\alpha}{tg\beta}\right) =\left[\frac{\left(\frac{h}{p}\right)}{\left(\frac{h}{p’}\right)}\right]$$\Leftrightarrow$$ \left(\frac{tg\alpha}{tg\beta}\right) = \left[\left(\frac{\not {h}}{p}\right)\times\left(\frac{p’}{\not {h}}\right)\right]$
$\color{Navy}{\left(\frac{tg\alpha}{tg\beta}\right) = \left(\frac{p’}{p}\right)}$ (IX)
Substituindo as equações (VII) e (IX) em (III), vamos ter:
$\left(\frac{p’}{p}\right)\times\left({p + R}\right) = \left(\frac{n_{2}}{n_{1}}\right)\times\left({p’ – R}\right)$
Efetuando as multiplicações:
$\left(\frac{p’p + p’R}{p}\right) = \left(\frac{n_{2}\times p’ – n_{2}\times R}{n_{1}}\right)$
Multipicando os extremos e meios da proporção:
${n_{1}p’p + n_{1}p’R = n_{2}p’p – n_{2}pR}$
Dividindo todos os termos pelo produto$pp’R$
$\frac{n_{1}\times{\not{p’}\not{p}}}{\not{p’}\not{p}R} + \frac{n_{1}\times{\not{p’}\not{R}}}{\not{p’}\not{R}p} = \frac{n_{2}\times{\not{p’}\not{p}}}{\not{p’}\not{p}R} – \frac{n_{2}\times{\not{p}\not{R}}}{p’\not{p}\not{R}}$
Colocando termos semelhantes de um mesmo lado:
$\frac{n_{1}}{p} + \frac{n_{2}}{p’} = \frac{n_{2}}{R} – \frac{n_{1}}{R}$
$\color{Navy}{\frac{n_{1}}{p} + \frac{n_{2}}{p’} = \left({n_{2} – n_{1}}\right)\times\left(\frac{1}{R}\right)}$
Se a incidência da luz no dioptro for no sentido do meio em que se encontra o centro de curvatura, a figura fica assim:
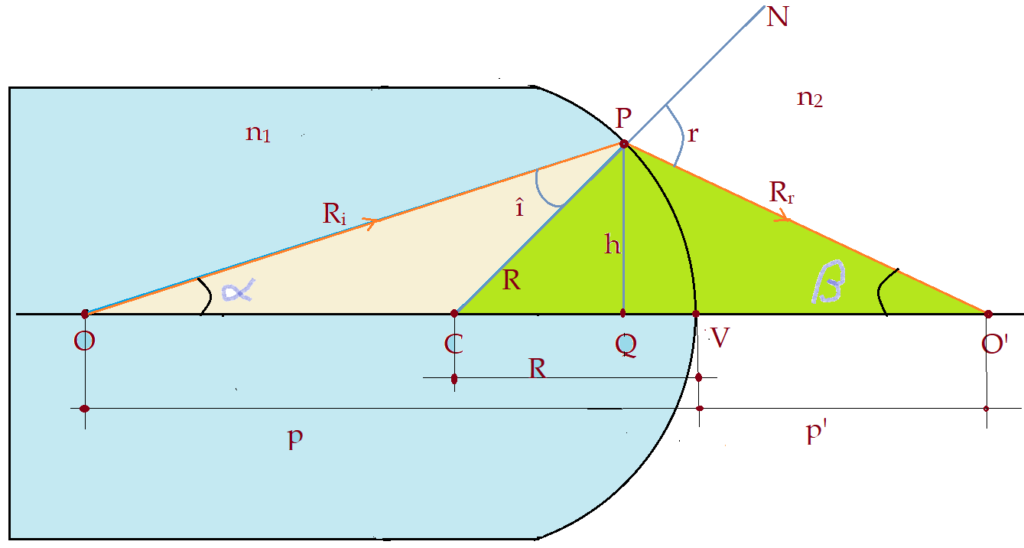
Aplicando o raciocínio semelhante, chegaremos à mesma fórmula que encontramos no primeiro caso. Iremos apenas substituir o raio de curvatura por seu valor negativo.
Podemos observar o que acontece nos dioptros côncavos. Veja as duas figuras que seguem.
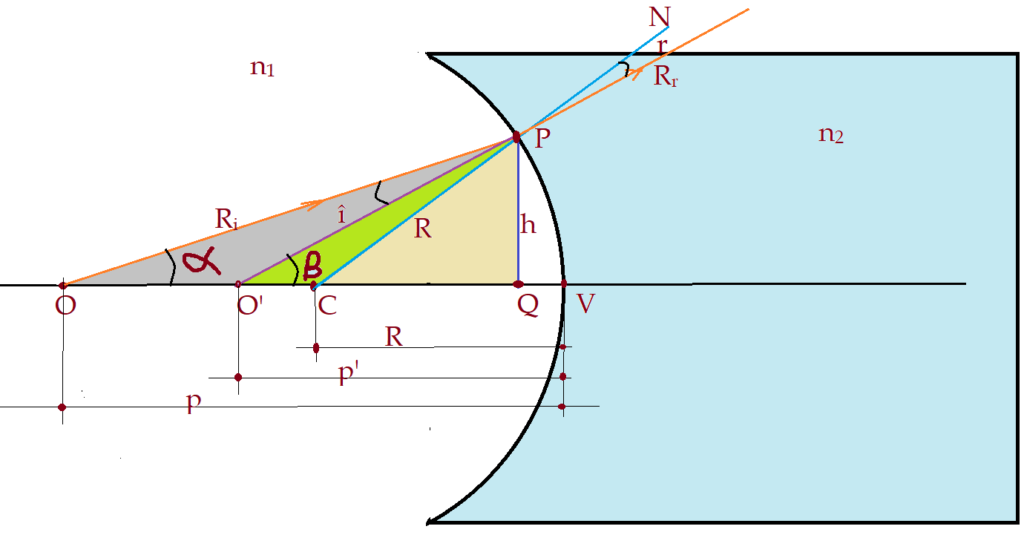
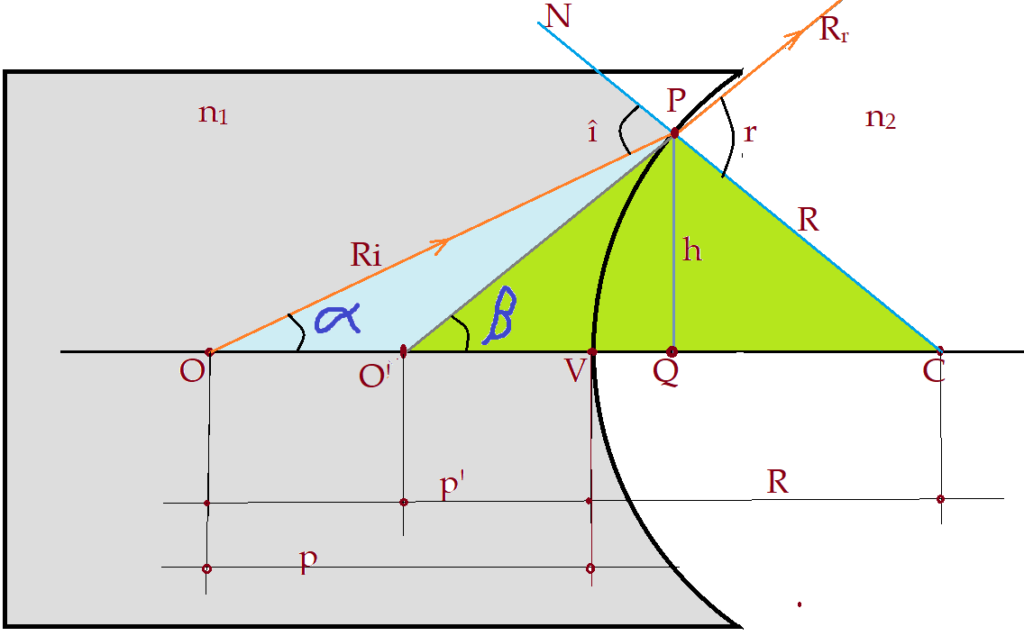
Fazer demonstrações dessas fórmulas, que acabariam dando o mesmo resultado é tempo gasto desnecessariamente. Vamos ao ponto que nos interessa de fato. Equação dos fabricantes de lentes. Veja a ilustração que segue:
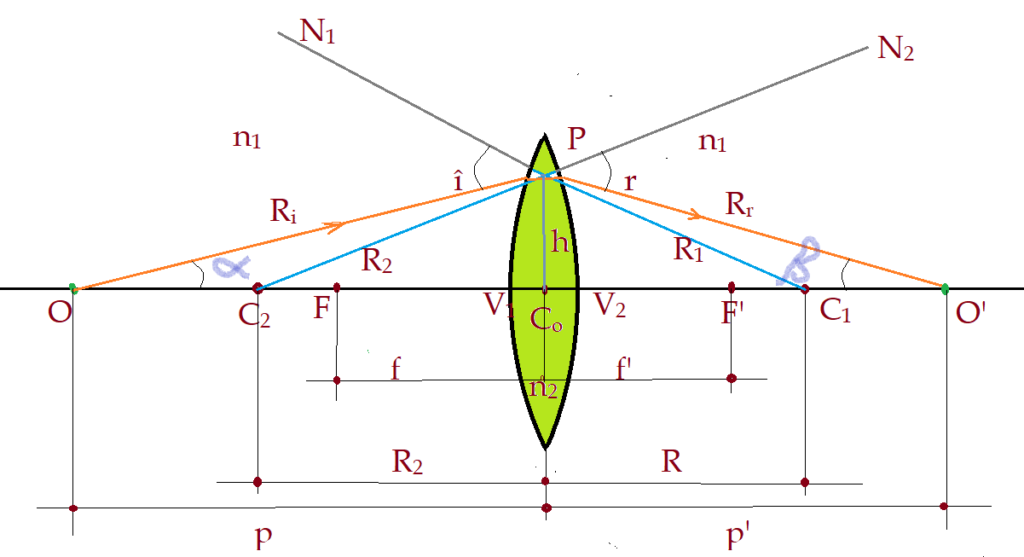
Vimos no estudo dos dioptros esféricos que:
$\frac{n_{1}}{p} + \frac{n_{2}}{p_{1}’} = \left({n_{2} – n_{1}}\right)\times\left(\frac{1}{R_{1}}\right)$ (XI)
No segundo dioptro, teremos a imagem real do primeiro, como objeto virtual, ou seja $\color{Maroon}{p = p_{1}’}$ e a posição da imagem será $\color{Maroon}{p’}$. O índice de refração da lente $\color{Maroon}{n_{2}}$ é agora o meio do qual a luz passa para o outro meio $\color{Maroon}{n_{1}}$. A equação irá ficar:
$\left(\frac{-{n_{2}}}{p_{1}’} + \frac{n_{1}}{p’}\right) = \left({n_{2} – n_{1}}\right)\times \left(\frac{1}{R_{2}}\right)$
Somando as equações membro a membro, vamos ter:
$\left[\left({{n_{1}\over p} + {n_{2}\over {p_{1}’}}}\right) + \left({{{-{n_{2}\over p_{1}’}} + {n_{1}\over p’}}}\right)\right] = \left[{\left({n_{2} – {n_{1}}}\right)\cdot\left({1\over {R_{1}}}\right) + \left({n_{2} – n_{1}}\right)\cdot\left({ 1\over{R_{2}}}\right)}\right]$
$\frac{n_{1}}{p} + \frac{n_{1}}{p’} = \left({n_{2} – n_{1}}\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)$
Dividindo a equação por $\color{Maroon}{n_{1}}$, chegaremos ao nosso objetivo.
$\left(\frac{\frac{\not{n_{1}}}{p}}{\not{n_{1}}}\right) + \left(\frac{\frac{\not{n_{1}}}{p’}}{\not{n_{1}}}\right) = \left[\left(\frac{n_{2}}{n_{1}} – \frac{\not{n_{1}}}{\not{n_{1}}}\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)\right]$
$\color{Navy}{\frac{1}{f}=\frac{1}{p} + \frac{1}{p’} = \left(\frac{n_{2}}{n_{1}} – 1\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)}$
Temos aí a equação dos fabricantes de lentes.
Convergência ou vergência de uma lente
Denominamos convergência ou vergência de uma lente ao inverso da distância focal.
$\color{Navy}{V = \frac{1}{f}}$
Unidade de convergência é o inverso da unidade de medida de comprimento:
No SI: $V= \frac{1}{m} = m^{-1}$
Essa unidade recebe o nome de dioptria (di).
Assim $\color{Maroon}{V = 1\,di}$ significa que a distância focal da lente é $\color{Blue}{f = 1\,m}$
Combinando a equação dos fabricantes com a dos pontos conjugados, teremos:
$\color{Navy}{V = \frac{1}{f} = \frac{1}{p} + \frac{1}{p’}= \left(\frac{n_{2}}{n_{1}}-1\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)}$
Agora podemos resolver uma grande variedade de exercícios. Esta equação combina as propriedades físicas (índices de refração) com as características geométricas das lentes (raios de curvatura, distância focal e abcissas de objeto/imagem).
01. Uma lente plano-convexa é feita de material cujo índice de refração é $\color{Maroon}{n_{2} = 1,5}$. O raio de curvatura da face convexa é $\color{Maroon}{R_{2} = 0,80\,m}$. Considerando a lente no ar, determinar a distância focal e a convergência da mesma.
Dados: $n_{2} = 1,5$;$R_{2} = 0,80 m$;$n_{1} = 1$;$R_{1} =\infty$
$V = \left(\frac{n_{2}}{n_{1}} + 1\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)$
$V = \left(\frac{1,5}{1} -1\right)\times\left(\frac{1}{0,80} + \frac{1}{\infty}\right)$
$V = \left({1,5 – 1}\right)\times\left({1,25 + 0}\right)$$\Leftrightarrow$$V =\left({{0,5}\times{1,25}}\right)$
$\color{Navy}{V = 0,625\,di}$
$V = \frac{1}{f}$$\Leftrightarrow$$f = \frac{1}{V}$
$\color{Navy}{f = \frac{1}{0,625} = 1,60\,m}$
02. Suponhamos a lente do primeiro exemplo, porém com a face esférica côncava, mantendo os demais dados inalterados. Qual será a convergência e a distância focal dessa lente?
Dados: $R_{2} = -0,80 m$; $n_{2} = 1,5$; $n_{1} = 1$ e $R_{1} =\infty$
$V =\left(\frac{n_{2}}{n_{1}} – 1\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)$
$V = \left(\frac{1,5}{1} + 1\right)\times\left(\frac{1}{\infty} + \frac{1}{- {0,80}}\right)$
$V = \left({{1,5} – 1}\right)\times\left({0 – 1,25}\right)$$\Leftrightarrow$$V = \left({0,5}\times{- {1,25}}\right)$
$\color{Navy}{V = – 0,625\,di}$$\rightarrow$ é lente divergente, convergência $V\lt 0$
$f = \frac{1}{V}$
$\color{Navy}{f = \frac{1}{-{0,625}} = – 1,60\,m}$
03. Temos uma lente bi-convexa, cujos raios de curvatura medem respectivamente $\color{Maroon}{R_{1} = 0,40\,m}$ e $\color{Maroon}{R_{2} = 0,50\,m}$, sendo sua convergência $\color{Maroon}{V = 2,25\,di}$. Determine a distância focal e o índice de refração do material de que ela é feita. Se colocarmos um objeto real perpendicularmente ao eixo ótico, a distância $\color{Maroon}{p = 0,80\,m}$, onde se formará a imagem e qual a sua natureza?
Dados: $R_{1} = 0,40\,m$; $R_{2} = 0,50\,m $, $V = 2,25\,di$ e $p = 0,80\,m$
$V =\left(\frac{n_{2}}{n_{1}} – 1\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)$
$2,25 = \left(\frac{n_{2}}{1} – 1\right)\times\left(\frac{1}{0,40} + \frac{1}{0,50}\right)$$\Leftrightarrow$$2,25 = \left({n_{2} – 1}\right)\times\left({2,5 + 2,0}\right)$
$2,25 = \left({n_{2} – 1}\right)\times{4,5}$$\Leftrightarrow$$2,25 = {4,5}\times n_{2} – {4,5}$
$2,25 + 4,5 = {4,5}\times n_{2}$$\Leftrightarrow$$ n_{2} = \frac{6,25}{4,5}$
$\color{Navy}{n_{2} = 1,5}$
$f = \frac{1}{V}$$\Leftrightarrow$$ f = \frac{1}{2,25}$
$\color{Navy}{f \simeq {0,444}\,m}$
$V = \frac{1}{p} + \frac{1}{p’}$$\Leftrightarrow$$ 2,25 = \frac{1}{0,80} + \frac{1}{p’}$
$2,25 = 1,25 + \frac{1}{p’}$$\Leftrightarrow$$ 2,25 – 1,25 = \frac{1}{p’}$
$1 = \frac{1}{p’}$$\Leftrightarrow$$ p’ = \frac{1}{1}$
$\color{Navy}{p’ = 1,0\,m}$
A ampliação será dada por $A = -\frac{p’}{p} = -\frac{1}{0,80}$
$\color{Navy}{A = – 1,25}$
Abcissa da imagem $\color{Maroon}{p’ > 0}$ e ampliação $\color{Maroon}{A < 0}$, significam uma imagem real, invertida e maior que o objeto.
04. Em uma lente côncava-convexa, os raios de curvatura são $\color{Maroon}{R_{1} = – 1,00\,m}$, $\color{Maroon}{R_{2} = 0,50\,m}$. O índice de refração do material que constitui a lente é $\color{Maroon}{n_{2} =1,5}$, imersa no ar. Determinar a vergência dessa lente e sua distância focal. Um objeto de $\color{Maroon}{h = 6,0\,cm}$ é colocado perpendicularmente ao eixo principal, na posição $\color{Maroon}{p = 0,40\,m}$. Onde se formará a imagem? Qual é sua ampliação e natureza?
Dados: $R_{1} = – 1,00 m$; $R_{2} = 0,50 m$; $n_{2} =1,5$; $p = 0,40 m$ e $n_{1} = 1$
$V = \left(\frac{n_{2}}{n_{1}} – 1\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)$
$V = \left(\frac{1,5}{1} – 1\right)\times\left(\frac{1}{-1,0} + \frac{1}{0,50}\right)$$\Leftrightarrow$$V = \left({1,5 – 1}\right)\times\left({-1,0} + {2,0}\right)$
$\color{Navy}{V ={0,5}\times{1,0}= 0,5\,di}$
$f = \frac{1}{V}$$\Leftrightarrow$$ f = \frac{1}{0,5}$
$f = 2,0\,m$$\rightarrow$ a lente é convergente pois $A\gt0$ e $f\gt0$.
$V = \frac{1}{p} + \frac{1}{p’}$
$0,5 = \frac{1}{0,40} + \frac{1}{p’}$$\Leftrightarrow$${0,5} = 2,5 + \frac{1}{p’}$
${0,5} – {2,5} = \frac{1}{p’}$$\Leftrightarrow$$p’ = \frac{1}{-{2,0}}$
$\color{Navy}{p’ = -0,50\,m}$
$A = – \frac{p’}{p}$$\Leftrightarrow$$ A = \frac-{-{0,50}}{0,40}$
$\color{Navy}{A = 1,25}$
$A = \frac{I}{O}$$\Leftrightarrow$${A\times O} = I$
$\color{Navy}{I = 1,25\times 6,0 = 7,5\,cm}$
Sendo $f\gt 0$e $A\gt 0$, concluímos que a imagem é virtual e maior que o objeto.
05. Uma lente bi-côncava, tem raios de curvatura $\color{Maroon}{R_{1} = – 0,25\,m}$ e $\color{Maroon}{R_{1} = – 0,40\,m}$ . O índice de refração do material da lente é $\color{Maroon}{n_{2} = 1,6}$ e ela está imersa em um meio rarefeito, onde o índice de refração é $\color{Maroon}{n_{1} = 0,8}$. Determinar a vergência e a distância focal. Classifique a lente e diga que tipo de imagem é obtida para qualquer objeto real colocado sobre o eixo principal de modo perpendicular.
Dados: $R_{1} = – 0,25\,m$; $R_{1} = – 0,40\,m$; $n_{2} = 1,6$; $n_{1} = 0,8$
$V = \left(\frac{n_{2}}{n_{1}} – 1\right)\times\left(\frac{1}{R_{1}}+ \frac{1}{R_{2}}\right)$
$V = \left(\frac{1,6}{0,8} – 0,8\right)\times\left(\frac{1}{- 0,25}+ \frac{1}{- 0,40}\right)$$\Leftrightarrow$$V = \left({2 -0,8}\right)\times\left({-4 – 2,5}\right)$
$\color{Navy}{V = 1,2\times 6,5= – 7,8,di}$
$f = \frac{1}{V}$
$\color{Navy}{f = \frac{1}{-7,8}\simeq{-0,128}}$
Sendo $A\lt 0$ e $f\lt 0$, a lente é divergente, tem bordos espessos e forma somente imagens virtuais, direitas e menores para qualquer objeto real, colocado à qualquer distância próxima. Para um objeto colocado no infinito, a imagem será virtual, puntiforme e localizado no foco imagem, antes da lente. Estas imagens não podem ser projetadas, apenas visualizadas diretamente na lente.
06. Uma lente é convexa-côncava. Seus raios de curvatura são $R_{1} = 0,80 m$ e $R_{2} =-0,50m$. O índice de refração da lente é $n_{2} = 1,5$ e está imersa no ar. Qual é a vergência da lente? Qual é a distância focal da lente e sua natureza? Qual o tipo de imagem que se pode obter com essa lente?
Dados: $R_{1} = 0,80\,m$; $R_{2} =- 0,50\,m$; $n_{2} = 1,5$ e $n_{1} = 1$
$V = \left(\frac{n_{2}}{n_{1}} – 1\right)\times\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)$
$V = \left(\frac{1,5}{1} – 1\right)\times\left(\frac{1}{0,80} +\frac{1}{-0,50}\right)$$\Leftrightarrow$$V = \left({1,5 – 1}\right)\times\left({1,25 – 2}\right)$
$\color{Navy}{V =0,5\times -0,75 = – 0,375\,di}$
$f = \frac{1}{V}$
$\color{Navy}{f = \frac{1}{-0,375}\simeq{-2,67}\,m}$
A vergência é $V\lt 0$ e $f\lt 0$$\rightarrow$ o que nos dá uma lente divergente, de bordos espessos. As imagens de objetos reais são sempre virtuais, direitas e menores que o objeto, reduzindo-se a um ponto para o objeto no infinito.
Hora de exercitar por conta
01. Uma lente côncavo-convexa tem raios de curvatura iguais a $\color{Maroon}{R_{1} = 40\,cm}$ e $\color{Maroon}{R_{2} = 20\,cm}$. O índice de refração da lente é $\color{Maroon}{n_{2} = 2}$ e está imersa no ar. Determine:
a) sua distância focal;
b) sua convergência em dioptrias;
c) a posição da imagem de um objeto colocado a $p = 30 cm$ dessa lente.
d) calcule sua ampliação e descreva sua natureza.
02. Uma lente esférica delgada apresenta distância focal $\color{Maroon}{f = – 20\,cm}$. Classifique essa lente e calcule sua vergência.
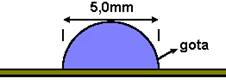
03. (UNIFESP-SP) – Um estudante observa uma gota de água, em repouso sobre sua régua de acrílico, como ilustra a figura. Curioso percebe que, ao olhar para o caderno de anotações através da gota, as letras do caderno aumentam e diminuem na medida em que aproxima ou afasta a régua do caderno. Fazendo alguns testes e observações, nota que a gota funciona como uma lente e que os efeitos do acrílico podem ser desprezados. Se a gota tem raio de curvatura igual $\color{Maroon}{R_{2} = 2,5\,mm}$ e o índice de refração da água vale $\color{Maroon}{n_{2} = 1,35}$ e o ar tem $\color{Maroon}{n_{1} = 1}$, determine a distância focal da lente plano-convexa formada, sua vergência e classifique a lente.
04. (UNIFESP-SP) – Tendo-se em vista que as lentes são, na prática, quase sempre usadas no ar, a equação dos fabricantes de lentes costuma ser escrita na forma $\color{Maroon}{C = \left({n – 1}\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)}$. Nestas condições pode-se afirmar que uma lente plano-convexa cujo raio de curvatura $\color{Maroon}{R_{2} = 20\,cm}$ e tem índice de refração $\color{Maroon}{n_{2} =1,5}$, tem convergência igual a:
( )a) 0,5 di;
( )b) 1,0 di;
( )c) 1,5 di;
( )d) 2,0 di;
( )e) 2,5 di.
05. (UFC-CE) – Uma lente esférica delgada, constituída de material de índice de refração n, está imersa no ar $\color{Maroon}{n_{ar} =1,00}$. A lente tem distância focal $\color{Maroon}{f}$ e suas superfícies esféricas tem raios de curvatura são $\color{Maroon}{R_{1}}$ e $\color{Maroon}{R_{2}}$. Esses parâmetros obedecem a uma relação, conhecida como “equação dos fabricantes”, mostrada aqui: $\frac{1}{f} = \left({n – 1}\right)\times\left(\frac{1}{R_{1}} + \frac{1}{R_{2}}\right)$. Suponha que a lente seja bi-convexa e seus raios de curvatura sejam $\color{Maroon}{R_{1} = R_{2} = R}$, a distância focal é $\color{Maroon}{f}$ e o índice de refração $\color{Maroon}{n_{2} = 1,8}$. Essa lente é partida ao meio, dando origem a duas lentes plano-convexas iguais. O valor da distância focal das duas novas lentes é:

( )a) $\frac{f}{2}$;
( )b) $\frac{4\times f}{5}$;
( )c) $f$;
( )d) $\frac{2\times f}{5}$;
( )e) ${2\times f}$.
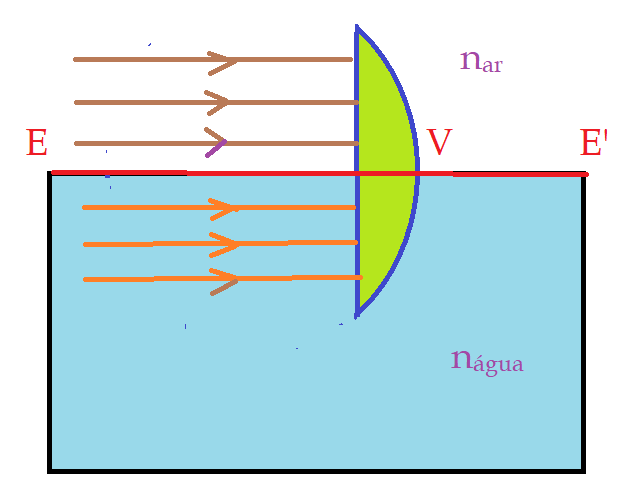
06. (UNESP-SP) – Em um laboratório, uma lente plano convexa, de raio de curvatura $\color{Maroon}{R_{2} = 0,5\,m}$, é parcialmente mergulhada em água, de modo que o eixo principal fique no mesmo plano da superfície de separação entre a água e o ar. Um feixe de raios paralelos, incidindo paralelamente a esse eixo, após passar pela lente converge para dois focos distintos. Na parte da lente imersa no ar, a convergência é $\color{Maroon}{V = 1,0\,di}$. Se o índice de refração do ar é $\color{Maroon}{n_{ar}= 1,0}$ e o da água é $\color{Maroon}{n_{água} = \frac{4}{3}}$, a convergência da parte da lente mergulhada no líquido é, em di:
( )a) $\frac{1}{4}$;
( )b) $\frac{3}{5}$;
( )c) $\frac{2}{3}$;
( )d) $\frac{3}{4}$;
( )e) $\frac{4}{5}$.
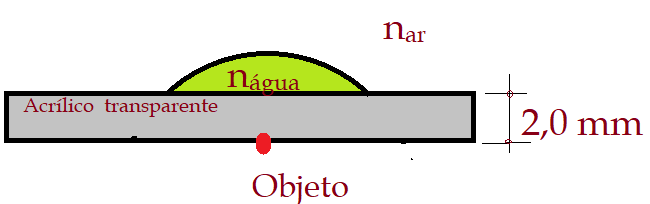
07. (UMTM-MG) – Em uma régua de acrílico transparente, pingou-se uma gota d’água. Devido às forças de coesão entre as moléculas e demais forças que agem sobre elas, a gota tomou a forma de uma pequena lente plano-convexa de raio de curvatura $\color{Maroon}{R_{2} = 3,0\,mm}$. Dados: $\color{Maroon}{n_{água} = 1,3}$ e $\color{Maroon}{n_{ar} =1,0}$. A espessura da régua é $\color{Maroon}{e = 2,0\,mm}$, quando ela é colocada sobre um texto escrito, as letras tem suas dimensões aumentadas em:
( )a) 25%;
( )b) 50%;
( )c) 75%;
( )d)100%;
( )e) 125%.
08. (FMTM-MG) – A face convexa de uma lente de vidro plano-convexa possui um raio de curvatura $\color{Maroon}{R_{2}=6,0\,cm}$.

Sendo o índice de refração do vidro igual a $\color{Maroon}{n_{2}=1,5}$, determine a distância focal da lente, em cm quando imersa no ar, cujo índice de refração é $\color{Maroon}{n_{1}=1,0}$.
09. (UFG) – Um indivíduo usa uma lente plano-convexa para concentrar raios solares sobre grama seca, visando fazer pequena fogueira. Para isso ele ajusta a lente na posição ótima. Sabendo-se que o índice de refração da lente é $\color{Maroon}{n_{2}= 1,5}$, o raio de curvatura do lado convexo é $\color{Maroon}{R_{2} = 10,0\,cm}$. Usando a equação dos fabricantes de lentes determine à que distância da grama ele posicionou a lente.

( )a) $p = 6,0\,cm$;
( )b) $p = 12,0\,cm$;
( )c) $p = 15,0\,cm$;
( )d) $p = 20,0\,cm$;
( )e) $p = 30,0\,cm$.
10. (UFU) – Lucas é o único sobrevivente de uma queda de avião e encontra-se sozinho numa região desabitada. Ele busca entre os destroços, objetos que possam ajudá-lo a sobreviver e encontra uma lupa. Lembrando-se de suas aulas de Física sobre lentes convergentes, Lucas decide usá-la para fazer uma fogueira. Acumulando alguns gravetos, ele posiciona sua lupa e observa que os raios solares convergem para um ponto situado a uma distância de 10 cm, proporcionando-lhe, após algum tempo, a fogueira desejada.


Ele resolve então usar a lupa para se divertir um pouco. Observando os pequenos objetos à sua volta, encanta-se com uma pequenina flor amarela, que, com o uso da lupa aparenta ser três vezes maior que o seu tamanho original. Com base nessas informações:
a) calcule o centro de curvatura da lente, admitindo que as faces sejam simétricas $\color{Maroon}{R_{1} = R_{2}}$;
b) determine à que distância em relação à flor Lucas posiciona a lupa.
11. (UFSCAR-SP) – Um livro de ciências ensina a fazer um microscópio simples com uma lente de glicerina. Para isso, com um furador de papel, faz-se um furo circular num pedaço de folha fina de plástico que, em seguida, é apoiada sobre uma lâmina de vidro. Depois, pingam-se uma ou mais gotas de glicerina, que preenchem a cavidade formada pelo furo, que se torna a base de uma lente líquida praticamente semi-esférica. Sabendo que o índice de refração absoluto da glicerina é $\color{Maroon}{n_{2}=1,5}$ e o diâmetro do furo é $\color{Maroon}{d= 5,0\,mm}$, pode-se afirmar que a vergência dessa lente é de aproximadamente:
( )a) $V=+ 10\,di$
( )b) $V = – 20\,di$
( )c) $V = + 5\,di$
( )d) $V = – 150\,di$
( )e) $V = + 200\,di$

12. (ITA-SP) – As duas faces de uma lente delgada bi-convexa, têm um raio de curvatura igual a $\color{Maroon}{R = 1,00\,m}$. O índice de refração para a luz vermelha é $\color{Maroon}{n_{ver}=1,6}$ e para a luz violeta é $\color{Maroon}{n_{vio}=1,64}$. Sabendo que ela está imersa no ar cujo índice de refração é $\color{Maroon}{n_{ar}= 1,0}$, calcule a distância em centímetros entre os focos da luz vermelha e violeta.
13. (Upe 2013) – Uma lente plano-côncava, possui um raio de curvatura $\color{Maroon}{R_{2}=30\,cm}$. Quando imersa no ar $\color{Maroon}{n_{1} = 1}$, a lente comporta-se como uma lente divergente de distância focal $\color{Maroon}{f = – 60\,cm}$. Assinale a alternativa que corresponde ao índice de refração $\color{Maroon}{n_{2}}$ dessa lente.
( )a) 0,5; ( )b) 1; ( )c) 1,5; ( )d) 2; ( )e) 2,5.
15. (Ufpr 2004) – Uma lente plano-convexa possui distância focal de $\color{Maroon}{f = 50\,cm}$ quando imersa no ar. O raio de curvatura da face convexa mede $\color{Maroon}{R_2 =20\,cm}$, e o material de que a lente é feita tem índice de refração igual a $\color{Maroon}{n_2 = 1,4}$. Considere um objeto situado sobre o eixo principal da lente, a uma distância de $\color{Maroon}{p = 60\,cm}$ dela. Se o sistema lente-objeto descrito for transposto para um meio com índice de refração igual a $\color{Maroon}{n_3 =1,5}$, é correto afirmar:
01) A lente passa a ser do tipo divergente;
02) A distância focal da lente não vai se alterar;
04) A imagem nessa situação será virtual, direita e menor que o objeto;
08) A imagem se formará a $p’ = – 50 cm$ da lente;
16) O aumento linear será de +1,2.
Havendo dúvidas, não hesite em procurar ajuda. Estamos sempre à disposição para esclarecer qualquer dificuldade.
Curitiba, 11 de dezembro de 2019.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
