Física – Mecânica – Movimento de queda livre
Rigorosamente falando, a queda livre de um corpo é o movimento de um corpo abandonado de uma altura qualquer acima da superfície da Terra ou outro astro do Universo, num ambiente de vácuo perfeito.
É fácil perceber que isso é pouco prático de executar em nosso dia a dia. Mas, se o corpo for de forma adequada e a altura não muito grande, teremos uma aproximação bastante razoável com experimentos realizados em condições ambientes. O corpo irá cair em movimento acelerado, até chocar-se com o solo. A aceleração é constante e denomina-se aceleração da gravidade. Ela é consequência da força de atração (peso) que a Terra exerce sobre o corpo. O valor aproximado da aceleração é $g = 9,81\,m\cdot s^{-2}$. No uso geral costuma-se considerar uma aproximação para $g = 10,0\,m\cdot s^{-2}$. Em situações onde a necessidade de exatidão é menos premente, esse arredondamento não chega a causar problemas.
O movimento de queda livre, também pode ser considerado como um lançamento vertical, cuja velocidade inicial é nula. Pode-se usar um referencial situado no solo ou no ponto de lançamento, como mostram as figuras a seguir.
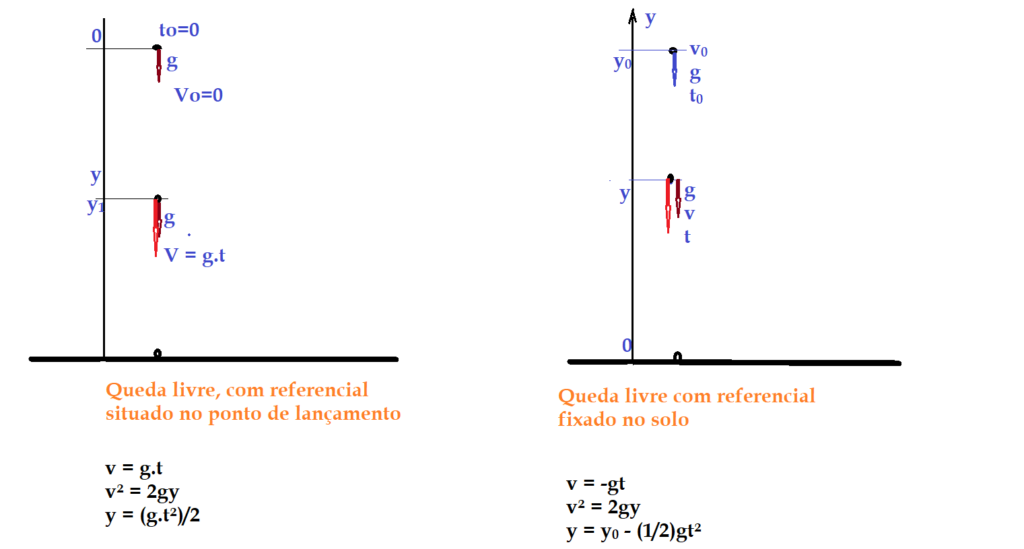
Em verdade os movimentos de queda livre podem ser incluídos no tipo mais amplo de movimento variado, os lançamentos verticais.
Um corpo pode ser lançado na vertical com velocidade inicial dirigida para cima ou para baixo, ficando a partir desse momento sob ação da aceleração da gravidade. Para resolver qualquer problema dessa natureza, usaremos as mesmas equações do MRUV, apenas substituiremos as variáveis $a$ por $g$ e $X$ por $Y$.
Teremos então: $\color{Brown}{V = V_{0} + g\cdot t}$
$\color{Brown}{V^{2} = {V_{0}}^{2} + 2\cdot g\cdot \Delta{Y}}$
$\color{Brown}{Y = Y_{0} + V_{0}\cdot t + \frac{1}{2}\cdot g\cdot t^{2}}$
Podemos resolver qualquer situação que envolva movimento vertical sob a ação da gravidade aplicando estas equações, desde que estejamos atentos aos sinais $\pm$, conforme o sentido tomado como positivo e o referencial adotado. A representação gráfica no plano cartesiano das grandezas é igual à do MRUV que já foi visto.
Exercícios resolvidos
- Uma esfera de chumbo cai de uma altura de $Y = 70,0\,m$, num local em que se pode considerar a aceleração da gravidade igual a $g = 10,0\,m\cdot s^{-2}$. Pede-se: a) qual é o tempo decorrido desde o início da queda, até o impacto no solo ?; b) com que velocidade o corpo atinge o solo?; c) em que instante do movimento ele está na metade da altura de onde cai?
Temos: $Y = 70,0\,m$
$g = 10,0\,m\times s^{-2}$
a) $Y = Y_{0} + V_{0}\cdot t + \frac{1}{2}\cdot g\cdot t^{2}$
$70,0 = 0 + 0 + \frac{1}{2}\cdot{10,0}\cdot t^{2}$
$70,0 = 5\cdot t^{2}$$\Leftrightarrow$$t^{2} = \frac{70}{5}$
$t = \sqrt{14}$$\Leftrightarrow$$\color{Brown}{t \simeq 3,74 s}$
b) $V^{2} = {V_{0}}^{2} + {2}\cdot{10,0}\cdot{70,0}$
$V^{2} = 1400$$\Leftrightarrow$$V = \sqrt{1400}$
$\color{Brown}{V \simeq 37,41\, m\cdot s^{-1}}$
c) $\frac{y}{2} = \frac{70,0}{2}\,m = 35,0\, m$$\Rightarrow$$t = ?$
$35,0 = \frac{1}{2}\cdot{10,0}\cdot t^{2}$$\Leftrightarrow$$35,0 = {5,0}\cdot t^{2}$
$t^{2} = \frac{35,0}{5,0}$$\Leftrightarrow$$t = \sqrt{7,0}$
$\color{Brown}{t \simeq 2,65 s}$
2. Uma esfera é lançada verticalmente para cima com velocidade de $V_{0} = 30,0\,m\cdot s^{-1}$. Se o lançamento é feito de um ponto situado à $Y_{0} = 20,0\,m$ acima do solo, sendo a aceleração da gravidade $g = 10,0\,m\cdot s^{-2}$, pergunto: a) quanto tempo depois do lançamento a esfera atinge sua altura máxima? b)qual é essa altura máxima? c) em que instante e com que velocidade a esfera retorna à altura inicial? d)em quanto tempo e com que velocidade a esfera atinge o solo.
Dados: $V_{0} = 30,0\,m\cdot s^{-1}$
$g = – 10,0\,m\cdot s^{-2}$
$Y_{0} = 20,0\,m$
a) a esfera atinge a altura máxima no momento em que a velocidade se torna nula $V = 0$.
$V = V_{0} + g\cdot{t}$$\Leftrightarrow$$ 0 = 30,0 + {(-10,0)}\cdot{t}$
$ 10,0\cdot t = 30,0$$\Leftrightarrow$$ t = \frac{30,0}{10,0}$$\Leftrightarrow$$\color{Brown}{t = 3,0\, s}$
b) Se a esfera atinge a altura máxima no instante $t = 3,0\,s$, basta usar a equação da velocidade e calcular $Y_{max}$
$Y_{max} = Y_{0} + V_{0}\cdot t + \frac{1}{2}\cdot g\cdot t^{2}$
$Y_{max} = 20,0 + {30,0}\cdot{3,0} + \frac{1}{2}\cdot{{-10,0)}\cdot{3,0}^{2}$
$Y_{max} = 20,0 + 90,0 + {(- 5,0)}{9,0}$$\Leftrightarrow$$Y_{max}= 110,0 – 45,0 = 65,0\, m $
A altura máxima atingida será de $\color{Brown}{y_{max} = 65,0\, m}$.
c)$Y = 20,0 m$$\Rightarrow$$t = ?$ e $v = ?$
$Y = 20,0 + {30,0}\cdot{t} + \frac{1}{2}\cdot{(-10,0)}\cdot{t^{2}}$
$20,0 = 20,0 + {30,0}\cdot{t} – 5,0\cdot{t^{2}}$
$0 = {30,0}\cdot{t} – {5,0}\cdot{t^{2}}$$\Leftrightarrow$$0 = t\cdot{30,0} – {5,0}\cdot t$
A esfera está na posição $Y = 20,0\, m$ no instante $t = 0\,s$ e quando $0 = 30,0 – 5,0\cdot t$
$5,0\cdot t = 30,0$$\Leftrightarrow$$t = \frac{30,0}{5,0} = 6,0\, s$
Passará novamente na posição $Y = 20,0\,m$ depois de um intervalo $t = 6,0\,s$. Metade gasto na subida até a altura máxima e outra metade para retornar ao ponto de partida.
Obs.: Isso nos mostra que a velocidade tem o mesmo módulo ao passar na ida e na volta no mesmo ponto.
d)$Y = 0$$\Rightarrow$$t = ?$ e $v = ?$
$Y = 20,0 + {30,0}\cdot t + \frac{1}{2}\cdot{(-10,0)}\cdot{t^{2}}$
$0 = 20,0 + {30,0}\cdot{t} – 5,0\cdot{t^{2}}$
Temos uma equação do segundo grau. Vamos simplificar por $5$ e resolver.
$0 = 4,0 + {6,0}\cdot t – t^{2}$
$t = \frac{6,0\pm\sqrt{{{6,0}^2}-{4}\cdot{(-1,0)}\cdot{(4,0)}}}{{2}\cdot{(1,0)}}$
$t = \frac {6 \pm \sqrt{36,0 + 16}}{2}$
$t = \frac{6 + 7,2}{2}$$\Rightarrow$$\color{Brown}{t \simeq 6,6\,s}$
$t = \frac{6 – 7,2}{2}$$\Rightarrow$$t \neq – 0,6\,s$
O móvel só tocará no solo no instante $t \simeq 6,6\,s$. O outro valor para $t$ é negativo, o que o torna inviável. Não existe tempo negativo.
$V = V_{0} + {g}\cdot{t}$
$V = 30,0 + {(-10,0)}\cdot{6,6}$$\Leftrightarrow$$\color{Brown}{V = 30,0 – 66,0 = -36,0\,m\cdot s^{-1}}$
Exercícios por resolver
- Uma pedra é abandonada do alto de um edifício de $45,0\,m$ de altura. Considerando $g = 10,0\,m\times s^{-2}$, pede-se: a) com que velocidade ela atingirá o solo? b) qual é o tempo que demora para atingir o solo? c) em que momento e com que velocidade ela passa na altura $Y = 25,0\,m$?
- Um projétil é atirado para cima na vertical, partindo da posição $Y_{0} = 0$, com velocidade inicial de $V_{0} = 300,0\,m\cdot s^{-1}s$. Supondo que $g = 10,0\,m\cdot s^{-2}$, determine: a) a altura em que se encontra quando sua velocidade estiver reduzida à metade da inicial; b) qual é a altura máxima que ele atinge; c) qual é o tempo gasto até a altura máxima; d) em quanto tempo ele atingirá o solo novamente;
- Um balão está subindo com velocidade constante de $V = 5,0\,m\cdot s^{-1}$, quando alguém solta no ar uma pedra. Sendo a altura do balão nesse instante igual a $Y_{0} = 150,0\,m$, $ g = 10,0\,m\cdot s^{-2}$, deseja-se saber: a) a que altura a pedra efetivamente começa a cair; b) em quanto tempo ela chega ao solo; c) qual a velocidade da pedra no instante do impacto com o solo; d) o instante e a velocidade da pedra ao passar pelo ponto de altura $Y = 100,0\,m$.
- Um dispositivo colocado a uma altura $y$, solta esferas metálicas em intervalos constantes de $\Delta{t} = 1,0\,s$. A aceleração da gravidade local é $g = 10,0\,m\cdot s^{-2}$. Quando a primeira esfera toca o solo, a quinta está iniciando o movimento. Determine: a) a altura das outras três esferas; b) as velocidades respectivas de cada uma nesse instante; c) a altura de onde elas caem e o tempo de queda de cada uma.
- Uma lançadeira de projéteis está colocada a uma altura $Y_{0} = 40,0\,m$. Os projéteis são lançados verticalmente para cima com velocidade inicial $V_{0} = 80,0\,m\times s^{-1}$. A aceleração da gravidade é $g = 10,0\,m\times s^{-2}$. Determine: a) a altura máxima que os projéteis alcançam; b) o tempo que demora para que os projéteis atinjam a altura máxima; c) em quanto tempo os projéteis retornam ao ponto de lançamento? d) com que velocidade os projéteis atingem o solo; e) qual é o tempo total gasto até chegarem ao solo.
- Um objeto de $m = 2\,kg$ cai de uma certa altura em relação ao chão, levando cerca de$t=0,5\,s$ para atingi-lo. Desconsiderando-se o efeito de forças dissipativas, caso um objeto de $m= 4\,kg$ fosse solto da mesma altura, o tempo de queda desse corpo seria igual a:
Dados: $g = 10\,m/s^{2}$
a) 1,0 s;
b) 1,5 s;
c) 0,5 s;
d) 0,25 s;
e) 0,75 s.
7. Um tijolo é lançado para cima, em um lançamento vertical, com velocidade inicial de 10 m/s. Desconsiderando os efeitos da resistência do ar, determine a altura máxima que esse tijolo é capaz de atingir.
Dados: $g = 10 m/s^{2}$
a) 10 m;
b) 5 m;
c) 15 m;
d) 7,5 m;
e) 12 m.
8. Quando solto no vácuo, um objeto chega ao chão após um tempo de $\Delta t= 1,5\,s$, em um local onde a gravidade é igual a $g=10\,m/s^{2}$. Assinale a alternativa que indica a altura aproximada em que esse objeto foi solto:
a) 15 m;
b) 12 m;
c) 5,25 m;
d) 11,25 m;
e) 17,5 m.
9. (PUCC) Um vaso de flores cai livremente do alto de um edifício. Após ter percorrido $\Delta y =320\,cm$, ele passa por um andar que mede $h=2,85\,m$ de altura. Quanto tempo ele gasta para passar por esse andar? Desprezar a resistência do ar e assumir $g = 10 m/s^{2}$
a) 1,0s;
b) 0,80s;
c) 0,30s;
d) 1,2s;
e) 1,5s.
10. (PUCC) Duas bolas A e B, sendo a massa de A igual ao dobro da massa de B, são lançadas verticalmente para cima, a partir de um mesmo plano horizontal com velocidades iniciais iguais. Desprezando-se a resistência que o ar pode oferecer, podemos afirmar que:
( )a) o tempo gasto na subida pela bola A é maior que o gasto pela bola B também na subida;
( )b) a bola A atinge altura menor que a B;
( )c) a bola B volta ao ponto de partida num tempo menor que a bola A;
( )d) as duas bolas atingem a mesma altura;
( )e) os tempos que as bolas gastam durante as subidas são maiores que os gastos nas descidas.
11. Entre os movimentos enumerados a seguir, quais são os que podem ser dados como exemplos de movimentos com aceleração constante?
(I) Queda da folha seca de uma árvore.
(II) Queda de uma laranja da árvore de um pomar.
(III) Viagem de um avião na ponte aérea Rio-São Paulo.
( )a) I e II;
( )b) I e III;
( )c) somente II;
( )d) II e III;
( )e) somente III.
12. (Puc-RJ) Duas bilhas de chumbo são lançadas verticalmente e simultaneamente da mesma altura, uma para cima e outra para baixo, com as mesmas velocidades (em módulo). Sabendo que a resistência do ar pode ser desprezada na situação descrita, diga qual das afirmações abaixo é a correta.
( )a) A bilha lançada para baixo chega ao solo primeiro e com velocidade maior que a bilha lançada para cima;
( )b) A bilha lançada para baixo chega ao solo primeiro e com velocidade menor que a bilha lançada para cima;
( )c) A bilha lançada para baixo chega ao solo primeiro e com velocidade igual a da bilha lançada para cima;
( )d) As duas bilhas chegam ao mesmo tempo ao solo e com velocidades iguais;
( )e) As bilhas chegam ao mesmo tempo ao solo, mas com velocidades diferentes.
13. Um paraquedista radical pretende atingir a velocidade do som. Para isto seu plano é saltar de um balão estacionário na alta atmosfera, equipado com roupas pressurizadas. Como nessa altitude o ar é muito rarefeito, a força de resistência do ar é desprezível. Suponha que a velocidade inicial do paraquedista em relação ao balão seja nula e que a aceleração da gravidade seja $g=10\,m/s^{2}$. A velocidade do som nessa altitude é de $v_{s}=300\, m/s$.
a) Calcule em quanto tempo ele atinge a velocidade do som;
b) Calcule a distância percorrida nesse intervalo de tempo.
14. Numa região onde $g = 10\,m/s^{2}$, uma partícula é abandonada de uma altura $H = 45\,m$. Desprezando a resistência do ar pede-se:
a) tempo de queda;
b) velocidade ao atingir o solo;
c) usando um eixo orientado para baixo, esboce os gráficos da velocidade escalar e do espaço em função do tempo.
15. Numa região em que $g = 10\,m/s^{2}$, uma partícula é lançada para baixo, de uma altura de $Y = 140\,m$, com velocidade inicial $v_{o}= 15\,m/s$. Depois de quanto tempo a partícula atinge o solo? (despreze a resistência do ar)
16. Um projétil de $m=2\,kg$ é lançado verticalmente para cima, a partir do solo, com velocidade de $V_{yo}=20\,m/s$. Determine:
Dados:$g = 10\,m/s^{2}$
a) o tempo total de subida do projétil;
b) a altura máxima atingida pelo projétil;
c) a velocidade do projétil nos instantes t = 1,0 s e t = 3,0 s. Explique o resultado obtido.
17. Um garoto, na sacada de seu apartamento, a $y= 20\,m$ de altura, deixa cair um biscoito, quando tem então a ideia de medir o tempo de queda desse biscoito. Desprezando a resistência do ar e adotando $g = 10\,m/s^{2}$, determine o tempo gasto pelo corpo para chegar ao térreo.
18. Abandonando um corpo do alto de uma montanha de altura H, este corpo levará $t=9\,s$ para atingir o solo. Considerando $g = 10\,m/s^{2}$, calcule a altura da montanha.
19. (UFRN) – Em um local onde o efeito do ar é desprezível, um objeto é abandonado, a partir do repouso, de uma altura $H$ acima do solo. Seja $H_{1}$ a distância percorrida na primeira metade do tempo de queda e $_{2}$ a distância percorrida na segunda metade do tempo de queda. Calcule a razão $\frac{H_{1}}{ H_{2}}$.
20. (UFPE) – Um pequeno objeto é largado do $15^{o}$ andar de um edifício e cai, com atrito do ar desprezível, sendo visto $t_{1}= 1\,s$ após o lançamento passando em frente à janela do $14^{o}$ andar. Em frente à janela de qual andar ele passará $t_{2}=2\,s$ após o lançamento? Admita $g = 10\,m/s^{2}$.
Se ficarem dúvidas, peço a gentileza de fazer contato e tirar as dúvidas. Os meios estão listados abaixo.
Curitiba, 25 de setembro de 2019.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
