Física – Mecânica
Cinemática – MRU
Como foi visto no post anterior, os movimentos podem receber diferentes classificações, dependendo do comportamento das variáveis que estão presentes e podem ser mensuradas ou avaliadas.
Denominamos assim ao movimento de qualquer móvel (corpo em movimento), que percorre uma trajetória reta com velocidade constante.
Comecemos pelo mais simples:
${\color{Blue}{Movimento\, Retilíneo\, Uniforme.\, Abreviado\, MRU.}}$
Consideremos uma linha reta, sobre a qual tomamos um ponto e associamos a ele o número 0 (zero) e denominamos esse ponto de origem. As posições do móvel no decorrer do tempo serão indicadas tomando a origem por referência. Isso determina a existência de duas semi-retas. É possível percorrer essa reta em dois sentidos e iremos adotar um deles como progressivo e o outro como retrógrado. Ao primeiro associaremos o sinal (+) e ao segundo o sinal (-).
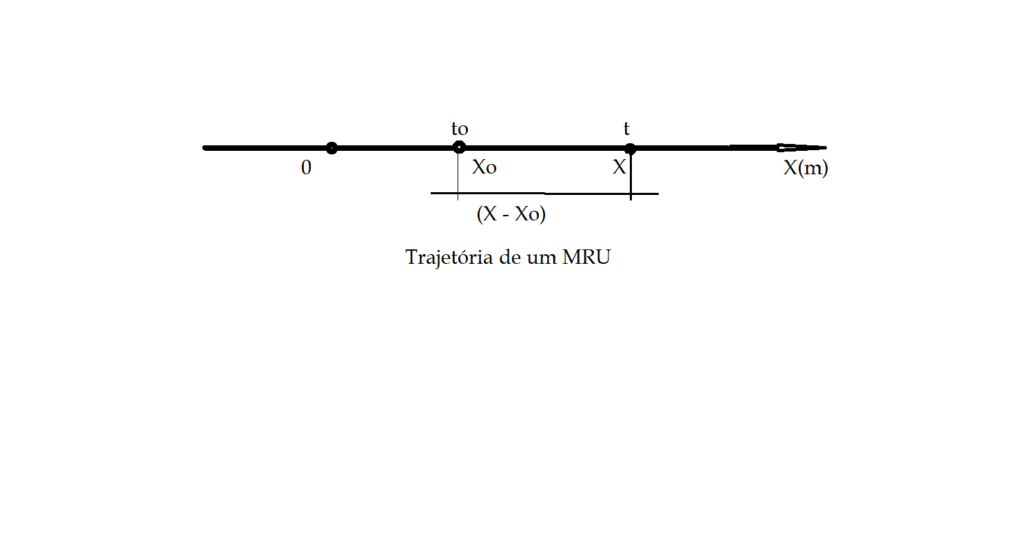
Se um móvel estiver em um ponto $\color{Blue}{ X_{0}}$, num instante de tempo $\color{Blue}{t_{0}}$ e em outro ponto $\color{Blue}{X}$, num instante $\color{Blue}{t}$, teremos que ele percorreu a distância
$\color{Brown}{X – X_{0} = \Delta{X}}$, no intervalo de tempo.
$\color{Brown}{t – t_{0} = \Delta{t}}$.
Se for verificado que ele percorreu distâncias iguais em tempos iguais, sua velocidade será constante e poderemos escrever:
$\color{Brown}{V =\frac{X -X_{0}}{t – t_{0}}}$
$\color{Brown}{V = \frac{\Delta{X}}{\Delta{t}}}$
A velocidade nos informa qual foi o deslocamento realizado na unidade de tempo.
Sempre que definimos uma nova grandeza, é imperioso estabelecer as unidades em que ela será medida. Sendo a velocidade obtida pela divisão entre o deslocamento e o intervalo de tempo, a unidade de velocidade será igual à razão entre a unidade de comprimento e a unidade de tempo.
No sistema SI:
$\Delta{X}$$\Rightarrow$ medido em metros ${m}$;
$\Delta{t}$$\Rightarrow$ medido em segundos ${s}$
$V =\frac{m}{s}$
$V = m\cdot{s^-{1}}$
No sistema técnico (antigo MKgfS): as unidades de deslocamento e tempo são as mesmas e portanto
$V = \frac{m}{s}$
$V = {m}\times{s^-{1}}$
No sistema CGS: $\Delta{X}$$\Rightarrow$ medido em centímetros ${cm}$
$\Delta{t}$$\Rightarrow$ medido em segundos ${s}$
$V = \frac{cm}{s}$
$V = {cm}\cdot{s^{-1}}$
OBS.: O sistema CGS caiu em desuso na grande maioria das situações, após o surgimento do SI. Apenas em alguns casos específicos é utilizado.
É comum encontrar algumas outras unidades de velocidade como é o caso do automobilismo: grande parte da humanidade usa o $km\times h^{-1}$; alguns países de língua inglesa usam o a $ milha\times h^{-1}$ e assim poderíamos citar uma infinidade de unidades usadas por grupos limitados de pessoas e em determinadas circunstâncias.
Defrontamo-nos com mais frequência com o $km/h$. Isso torna importante sabermos como proceder para converter essa unidade para as unidades do SI e demais. Para isso basta lembrarmos que:
$1 km = {10}^{3}\, m$
$1\,h = 60\, min = 60×60\, s = 3600\,s$
$\frac{1\,km}{1\,h} = \frac{{10}^3}{3,6\times{10^{3}}}\, m/s$$\Rightarrow$ cancelando o ${10}^{3}$ fica:
$\color{Brown}{1\, km\times h^{-1} = \frac{1}{3,6}\, m\times s^{-1}}$
Com uma simples regra de três podemos fazer a conversão de qualquer unidade para outra da mesma grandeza em outro sistema. Basta saber a correspondência unitária entre elas.
Equação horária do MRU
A partir da expressão da velocidade podemos obter uma equação que denominamos equação horária do MRU. Ela nos permite relacionar a posição do móvel, com o tempo de movimento. Seja:
$V = \frac{\Delta{X}}{\Delta{t}}$
$\Delta{X}= V \times \Delta{t}$
Substituindo $\Delta{X}$ por
$X – X_{0}$, ficamos com:
$X – X_{0} = V\times \Delta{t}$
$X = X_{0} + V\times \Delta{t}$
Via de regra o tempo inicial é considerado igual a zero $t_{0} = 0$, o que deixaria a expressão
$\Delta{t} = t – t_{0} = t$, dando à equação horária a forma que normalmente é usada:
$$\color{Brown}{X = X_{0} + V \cdot{ t}}$$
Lembrando do estudo de funções na matemática, vemos que a equação horária do MRU é uma função do primeiro grau. Vamos comparar?
$y = a\cdot {x} + b$$\Leftrightarrow$$\color{Brown}{ y = b + a\cdot{x}}$
$\color{Brown}{X = X_{0} + V \cdot{t}}$
A representação gráfica de $\color{Blue}{X = f(t)}$, resultará em uma reta.
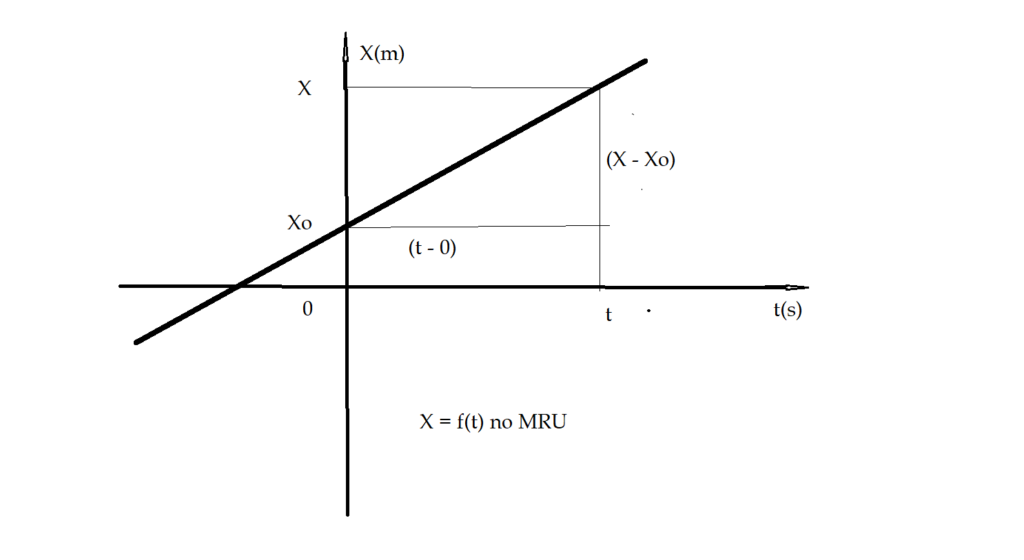
O gráfico é uma reta ascendente e neste caso o movimento é progressivo. Seria retrógrado se a reta fosse descendente.
Esta reta pode ser ascendente (movimento progressivo) e descendente (movimento retrógrado). $X_{0}$ é o termo independente e indica o ponto em que a reta irá cortar o eixo das ordenadas.
${V}$ é o coeficiente do termo em ${t}$ e por isso representa o coeficiente angular da reta, isto é, a tangente do ângulo entre a reta e o eixo representativo do tempo(abcissas).
$V = \frac{X – X_{0}}{t – t_{0}}$$\Leftrightarrow$$V = \frac{\Delta{X}}{\Delta{t}}$
A representação gráfica de $\color{Blue}{V = f(t)}$, no MRU, será uma reta paralela ao eixo das abcissas ${t}$. Acima da origem para os movimentos progressivos ${V>0}$ e abaixo da origem para os movimentos retrógrados ${V<0}$.
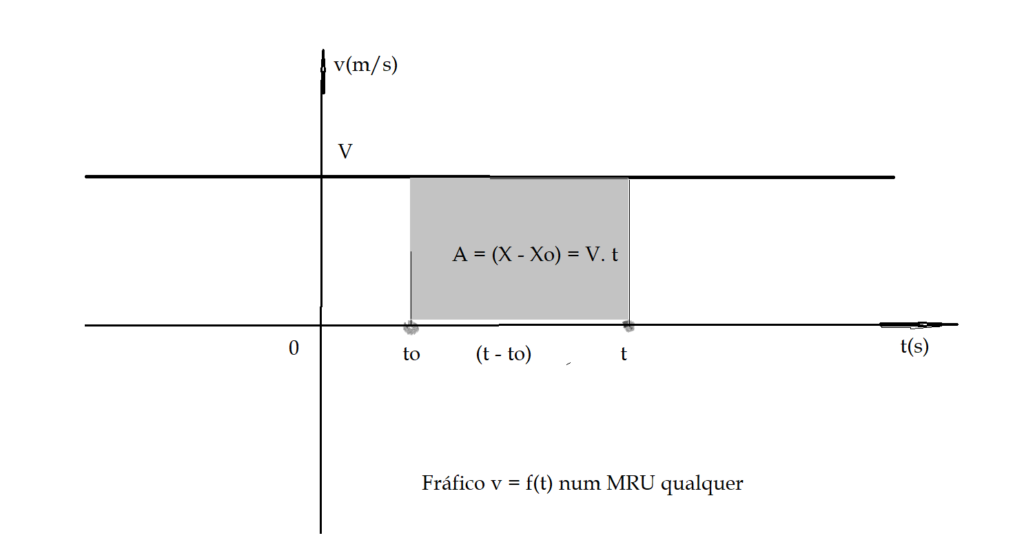
Num gráfico de $V = f(t)$ (velocidade em função do tempo), a área entre a reta e o eixo das abcissas, para um intervalo de tempo $\Delta{t} = t – t_{0}$ representará o deslocamento do móvel nesse intervalo. Se o movimento for retrógrado, $v\lt 0$, o gráfico ficará abaixo da origem, mantendo as demais características.
Exercícios resolvidos
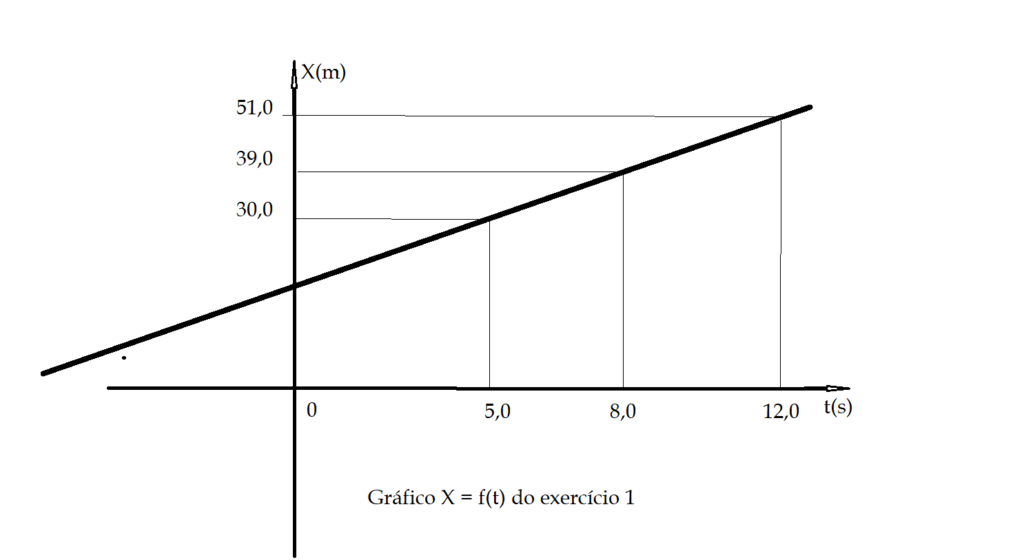
- Um móvel, no momento inicial, está na posição $X_{0} = 15,0\, m$ e se move com velocidade $V = {3,0}\, \frac{m}{s}$. Determine a posição do mesmo nos instantes $t = {5,0}\, s$; $t = {8,0}\, s$; $t = {12,0}\, s $. Represente graficamente o movimento num plano cartesiano $x = f(t)$. Trace também a reta representativa da velocidade em função do tempo, determinando o deslocamento entre os instantes $t = {5,0}\,s$ e $t = {12,0}\,s$.
- $X = X_{0} + V \times {t}$
- $X_{0} = 15,0\,m$
- $V = 3,0\,m/s$
- $X = ?$ quando $t = 5,0\, s$
- $X = 15,0 + {3,0}\times {5,0}$
- $X = 15,0 + 15,0 = 30\,m$
- $X = ?$ para $t = 8,0\,s$
- $X = 15,0 + {3,0}\times{8,0}$
- $X = 15,0 + 24,0 =39,0\,m$
- $X = ?$ para $t=12,0\,s$
- $X = 15,0 +{ 3,0}\times{12,0}$
- $X = 15,0 + 36,0 = 51,0\,m$
- A representação gráfica fica assim.
2. Um móvel encontra-se no ponto $X_{0} = 32,0\,m$, no instante $t_{0} = 0$, com velocidade$V = – 4,0\,\frac{m}{s}$ Em qual instante ele irá estar na origem da trajetória, isto é sua posição será $X = 0$? Em que momento ele estará na posição $X = – 32,0\,m$? Construa os gráficos de $X = f(t)$ e $V = f(t)$.
- $X_{0} = 32,0\,m$
- $V = – 4,0\,\frac{m}{s}$
- $X = 0$ para $t = ?$
- $X = X_{0} + {V}\times{t}$
- $0 = 32,0 + {-4,0}\times{t}$$\Leftrightarrow$${4,0\times {t} = 32,0}$
- $t = \frac{32,0}{4,0} = 8,0\, s$
- $X = -32,0\,m$ para $t = ?$
- $X = X_{0} + {v}\times{t}$
- $-32,0 = 32,0 + {-4,0}\times{t}$
- $4,0\times{t} = 32,0 + 32,0$
- $t = \frac{64,0}{4,0} = 16\,s$
Gráfico de $X = f(t)$.
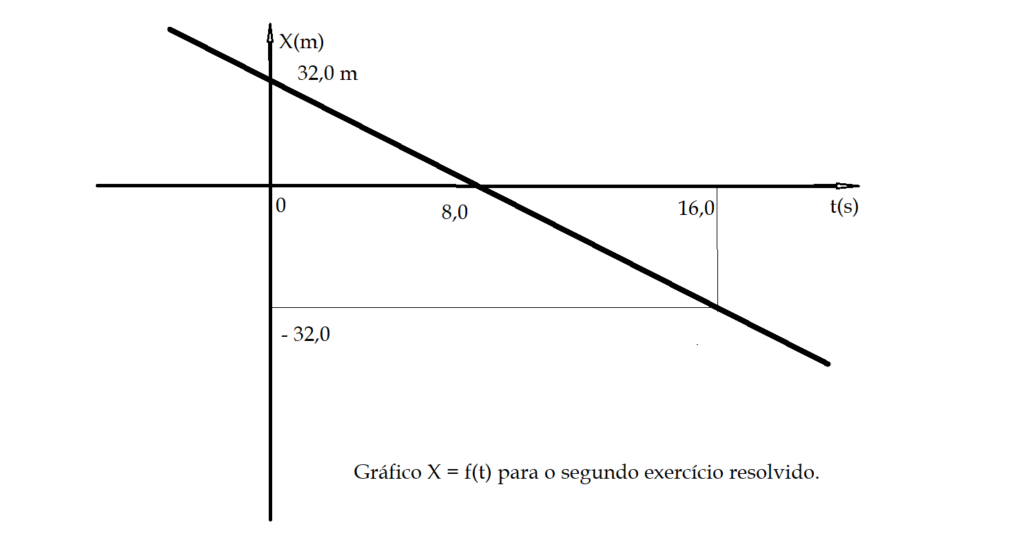
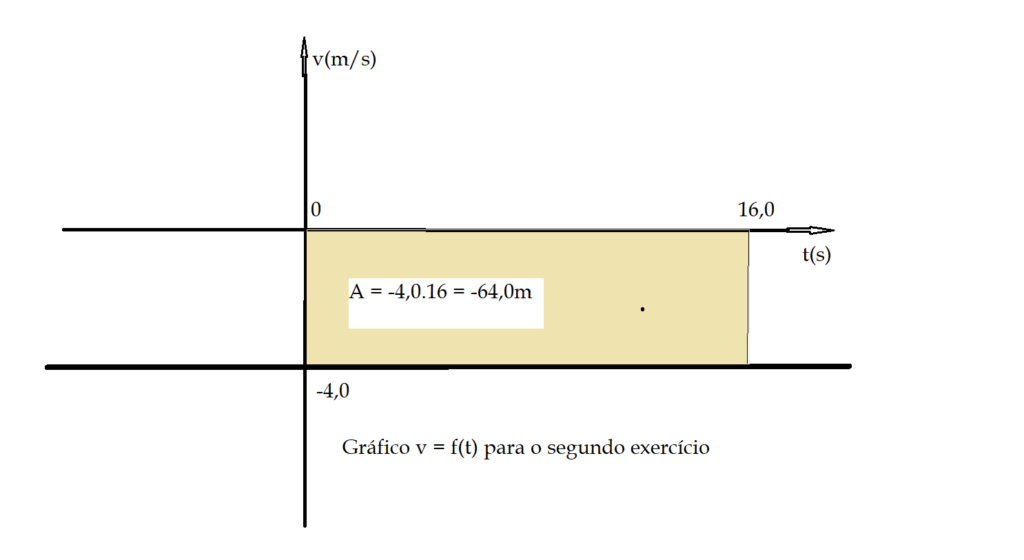
Gráfico $\color{Blue}{v = f(t)}$
3. Um móvel se dirige da posição $X_{0} = – 25,0\,m$, em movimento progressivo com velocidade de $V = 7,0\, \frac{m}{s}$, no instante $t =0\,s$. Em que posição ele estará no instante $t = 5,0\,s$? Em que instante ele irá passar pelo ponto$X = -4,0\,m$? E na posição$X = 24,0\,m$, quando irá passar? Construir o gráfico $X = f(t)$ e também $V = f(t)$, identificando o deslocamento no intervalo
- $X = X_{0} + {V}\times {t}$
- $X_{0} = -25,0\,m$
- $V = 7,0\,\frac{m}{s}$
- $t = 5,0\, s$$\Rightarrow$$X = ?$
- $X = – 25,0 + {7,0}\times{ 5,0}$
- $X = -25,0 + 35,0 = 10,0\,m$
- $X = -4,0\,m$$\Leftrightarrow$$t = ?$
- $-4,0 = – 25,0 + {7,0}\times {t}$
- $25,0 – 4,0 = {7,0}\times{t}$
- $21,0 = {7,0}\times {t}$
- $t = \frac{21,0}{7,0} = 3,0\,s$
- $X = 24,0\,m$$\Rightarrow$$t = ?$
- $24,0 = -25,0 + {7,0}\times {t}$
- $24,0 + 25,0 = {7,0}\times {t}$
- $49,0 = {7,0}\times {t}$
- $t = \frac{49,0}{7,0} = 7,0\,s$
Gráfico $\color{Blue}{X = f(t)}$
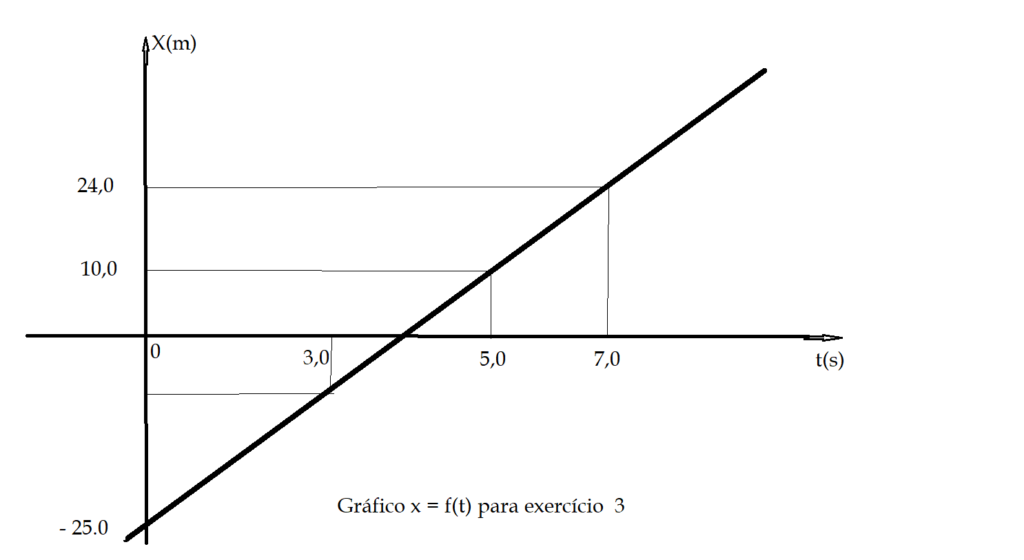
Gráfico $\color{Blue}{V = f(t)}$
Exercícios a resolver
- Um móvel, sobre uma trajetória retilínea horizontal, encontra-se na posição inicial $X_{0} = – 8,0\,m$, no instante $t_{0} = 0$. Sua velocidade é $V = 4,0\, \frac{m}{s}$. Determine: a) sua posição no instante $t = 6,0\,s$; b) o instante em que se encontra na origem da trajetória, isto é, $X = 0$; c) sua posição no instante $t = 10,0\, s$; d) construa os gráficos $X = f(t)$ e $V = f(t)$; e) classifique o movimento em função das características dos gráficos.
- O movimento retilíneo de um móvel é representado pelo gráfico abaixo.
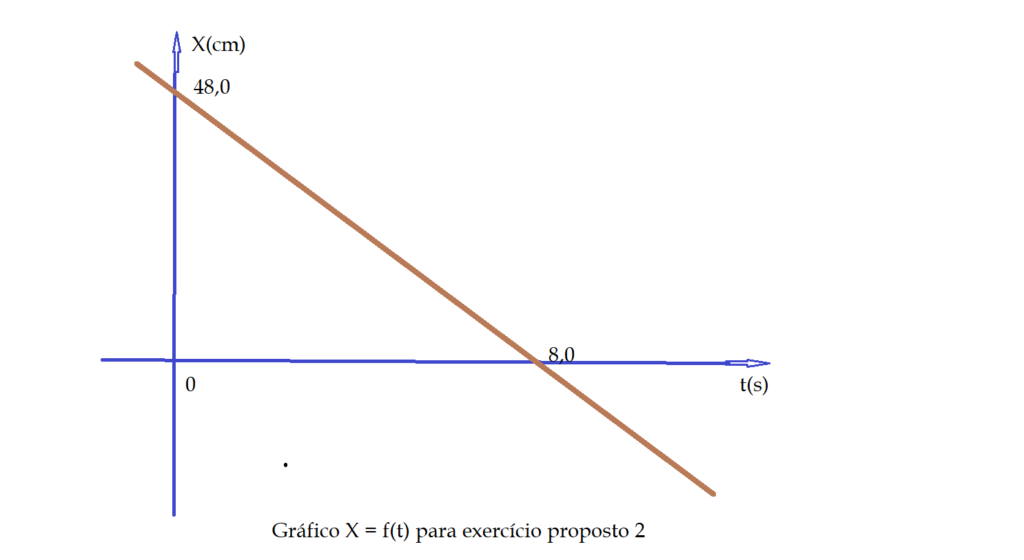
Determine, a partir do gráfico acima: a) a velocidade do móvel; b) a posição no instante $t = 3,0\,s$; c) o deslocamento no intervalo de tempo entre os instantes $t = 2,0\,s$ e $t = 9,0\,s$; d) classifique o movimento do móvel.
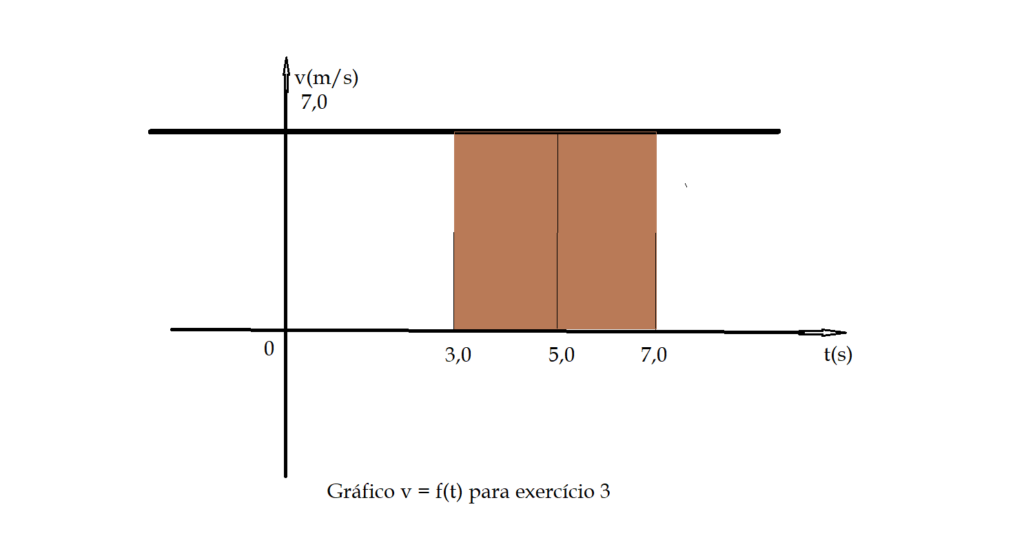
3) Um móvel em movimento retilíneo e uniforme, tem sua velocidade representada em função do tempo pelo gráfico abaixo.
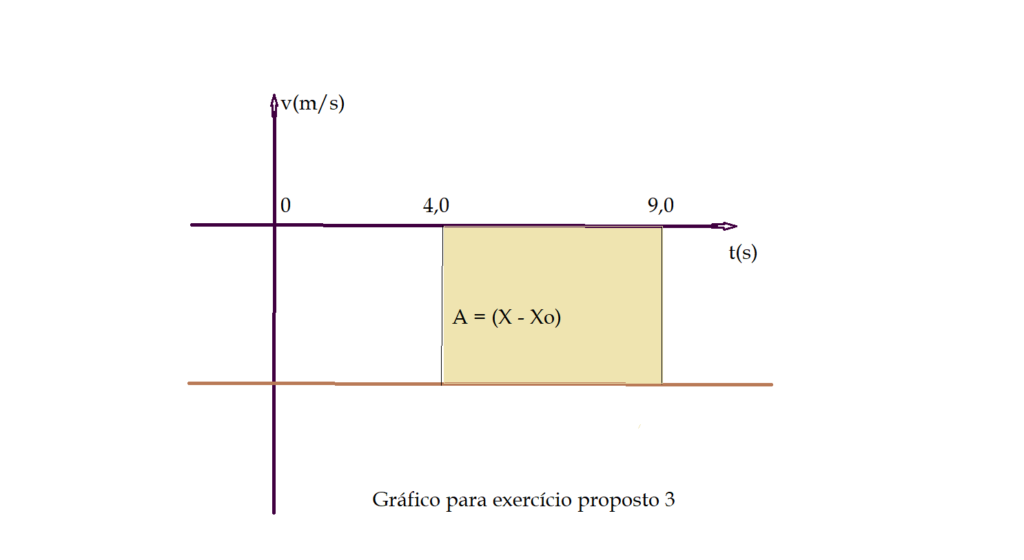
Determine: a) a velocidade do móvel; b) o deslocamento total do móvel desde o instante $t = 0$ até $t = 9,0\,s$; c) faça o gráfico $X = f(t)$, considerando $X_{0} = 28,0\,m$; d) classifique o movimento.
4) Se a velocidade de um móvel é $V = -5,0\,\frac{m}{s}$, sua posição inicial é $X_{0} = 28,0\,m$ no instante $t_{0} = 0$. Determine: a) a posição no instante $t = 3,0\,s$; b) o instante em que sua posição corresponde ao valor $X = 7,0\,m$; c) o momento em que sua posição é $X = 0$; d)faça os gráficos $X = f(t)$ e $V = f(t)$, classificando o movimento do móvel.
5) Um móvel parte da posição $X_{0} = -18,0\,m$, com velocidade $V = 4,0\, \frac{m}{s}$. Pede-se: a) o instante em que ele passa na origem $X = 0$; b) a posição do móvel no instante $t = 8,0\,s$; c) o deslocamento no intervalo entre o instante $t = 0$ e $t = 8,0\,s$; d) faça os gráficos $X =f(t)$ e $V = f(t)$, dando a classificação do movimento desse móvel.
6)Um móvel percorre trajetória reta com velocidade constante de $72,0\,\frac{km}{h}$ e no instante inicial $t_{0} =0$ ele se encontra na posição $X_{0} = 5,0\,m$. Qual será a posição em que ele estará no instante $t = 4,0\,s$? Em que momento ele estará na posição $X = 145,0\,m$
7)Um móvel parte da posição inicial $S_{o}= – 15\,m$ e, após 12 segundos, encontra-se na posição $S_{F}= 45\, $m.
a) Determine a velocidade média desse móvel.
b) Determine a função horária da posição do móvel.
c) Calcule a posição do móvel para os instantes t = 0 s, t = 1 s, t = 2 s, t = 3 s e t = 4 s. Em seguida, construa o gráfico de posição em função do tempo para esse movimento$S=f(t)$.
d) Classifique o movimento descrito por esse móvel.
8) Um móvel com velocidade constante percorre uma trajetória retilínea à qual se fixou um eixo de coordenadas. Sabe-se que no instante $t_{0} = 0$, a posição do móvel é $x_{0} = 500\,m$ e, no instante $t = 20\,s$, a posição é $x = 200\,m$. Determine:
a. A velocidade do móvel.
b. A função da posição.
c. A posição nos instantes $t = 1\,s$ e $t = 15\,s$.
d. O instante em que ele passa pela origem.
9) Dois carros A e B encontram-se sobre uma mesma pista retilínea com velocidades constantes no qual a função horária das posições de ambos para um mesmo instante são dadas a seguir: $x_{A} = 200 + 20\times t$ e $x_{B} = 100 + 40\times t$. Com base nessas informações, responda as questões abaixo.
a. É possível que o móvel B ultrapasse o móvel A? Justifique.
b. Determine o instante em que o móvel B alcançará o móvel A, caso esta situação aconteça.
10) A função horária do espaço de um carro em movimento retilíneo uniforme é dada pela seguinte expressão: $x = 100 + 8\times t$. Determine em que instante esse móvel passará pela posição $S=260\,m$.
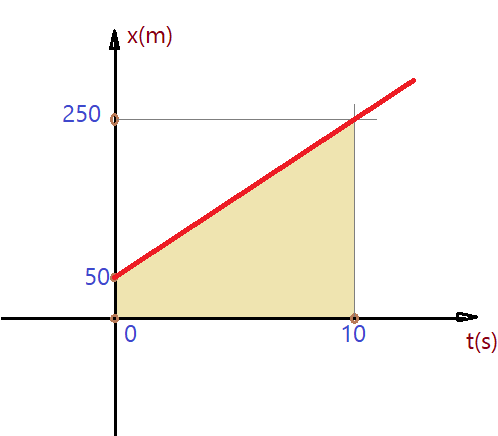
11) O gráfico a seguir representa a função horária do espaço de um móvel em trajetória retilínea e em movimento uniforme.
Com base nele, determine a velocidade e a função horária do espaço deste móvel. Com a área sob o gráfico determine o deslocamento no intervalo entre $t = 0$ e $t=10\,s$.
12)Um móvel em M.R.U gasta $10\,h$ para percorrer $X =1100\,km$ com velocidade constante. Qual a distância percorrida após $3 \,h$ da partida?
13) Um determinado móvel esta se deslocando em uma trajetória retilínea (M.R.U.) segundo a função horária $S = 4+28t$, em unidades SI. Pede-se:
- a) Determinar seu espaço inicial $S_{o}$.
- b) A velocidade do móvel no instante $t = 2\,s$.
- c) O espaço do móvel no instante $t=3\,s$.
- d) O deslocamento nos 5 primeiros segundos.
14. (PUC-MG) Um homem, caminhando na praia, deseja calcular sua velocidade. Para isso, ele conta o número de passadas que dá em um minuto, contando uma unidade a cada vez que o pé direito toca o solo, e conclui que são 50 passadas por minuto. A seguir, ele mede a distância entre duas posições sucessivas do seu pé direito e encontra o equivalente a seis pés. Sabendo que três pés correspondem a um metro, sua velocidade, suposta constante, é:
a) 3 km/h;
b) 4,5 km/h;
c) 6 km/h;
d) 9 km/h;
e) 10 km/h.
Se existirem dúvidas, faça contato por um dos canais abaixo citados para esclarecimentos. Não as guarde para si. Se tiver exercícios sobre o mesmo assunto, passados no seu colégio ou curso, pode igualmente perguntar. Basta mandar o enunciado ou os dados para que se possa analisar.
Curitiba, 12 de setembro de 2019.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular : e WhatsApp: (41) 99805-0732