Física – Mecânica
Movimento retilíneo uniformemente variado – MRUV
Parte I
Quando o movimento varia sua velocidade, aparece uma nova grandeza, que é denominada aceleração.
A aceleração mede a variação da velocidade na unidade de tempo.
Vamos ver como isso acontece. Suponhamos que um móvel tenha uma velocidade ${V_0 = 5,0\,m/s}$, num instante ${t_0}$ e depois de um intervalo ${\Delta {t} = 4,0\,s}$, ele passou a ter velocidade de ${V = 17,0\,m/s}$. Se o aumento de velocidade foi constante, isto é, aumentou igualmente a cada segundo transcorrido, estamos diante de uma aceleração constante. Podemos então escrever que:
- $a = \frac{V – {V_0}}{\Delta{t}}$$\Leftrightarrow$${a}\cdot\Delta{t} = V – V_{0}$
- Invertendo a ordem dos membros: $V – V_{0} = {a}\cdot\Delta{t}$
- $V = V_{0} +{a}\cdot\Delta{t}$
- se $V_{0} = 0$ e $t_{0} = 0$$\Leftrightarrow$$a=\frac{V}{t}$
- $\color{Brown}{V = {a}\cdot{t}}$
Os sinais da aceleração e da velocidade inicial $\pm$ nos darão a classificação do movimento em acelerado ou retardado. No movimento acelerado o módulo da velocidade aumenta e no movimento retardado o módulo da velocidade diminui.
Fica fácil deduzir que, se os sinais da aceleração e velocidade forem iguais, o módulo aumenta e o movimento é acelerado. Se os sinais forem opostos, o módulo da velocidade diminui e o movimento será retardado.
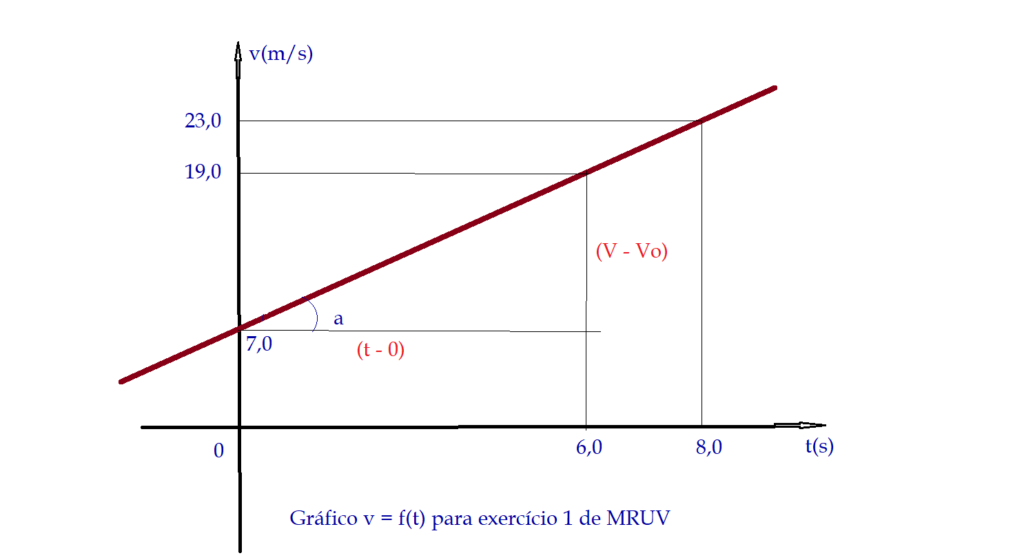
A representação gráfica da velocidade em função do tempo $\color{Blue}{V = f(t)}$, no MRUV é uma linha reta, pois podemos observar que a equação horária da velocidade $V = V_{0} + {a}\cdot{t}$ é uma função do primeiro grau (linear). Nesta reta o $V_{0}$ é o ponto em que a reta corta o eixo das ordenadas ${V}$ e recebe o nome de coeficiente linear ou termo independente. A aceleração por sua vez é igual ao coeficiente angular da reta, isto é, a tangente do ângulo que ela forma com o eixo das abcissas ou eixo do tempo ${t}$
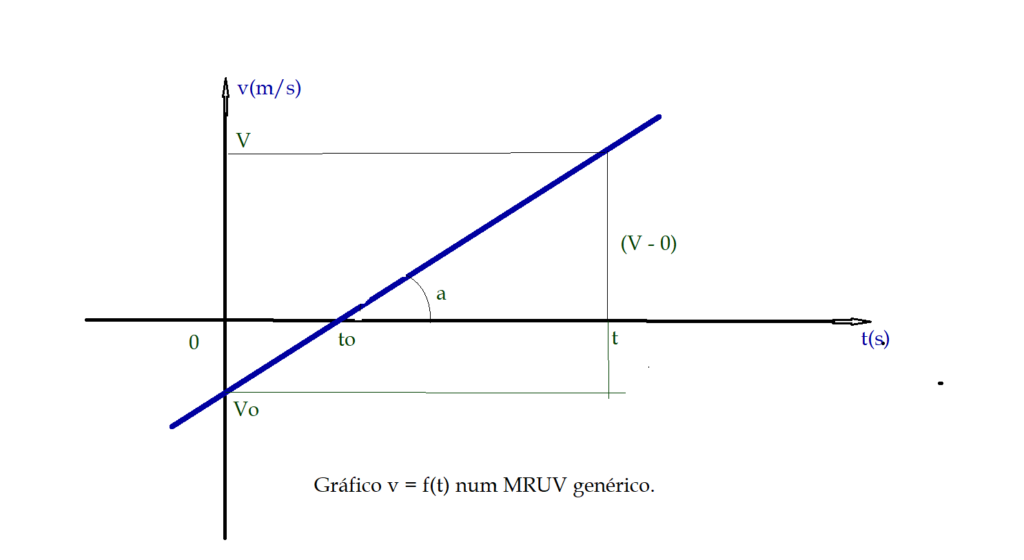
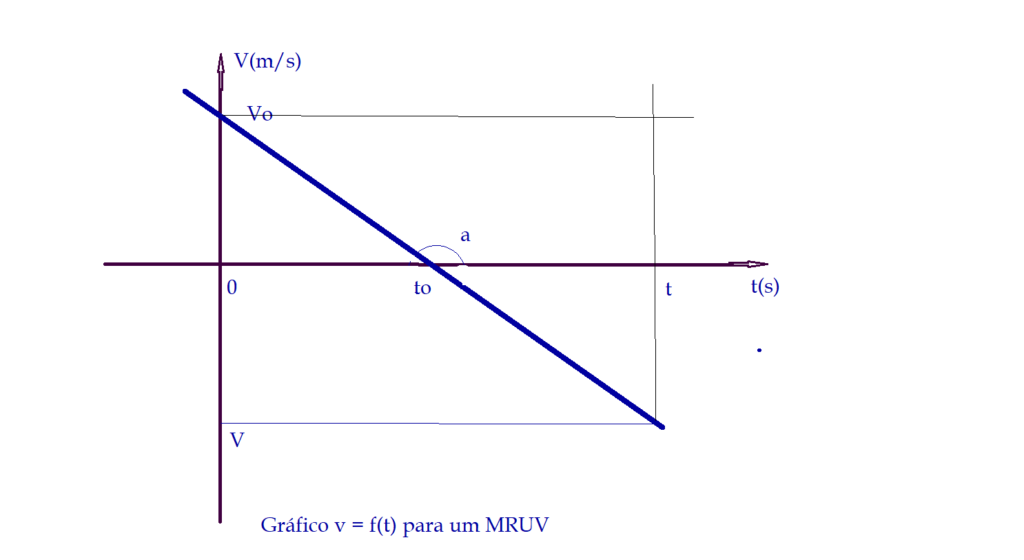
Movimento retardado progressivo e depois acelerado retrógrado.
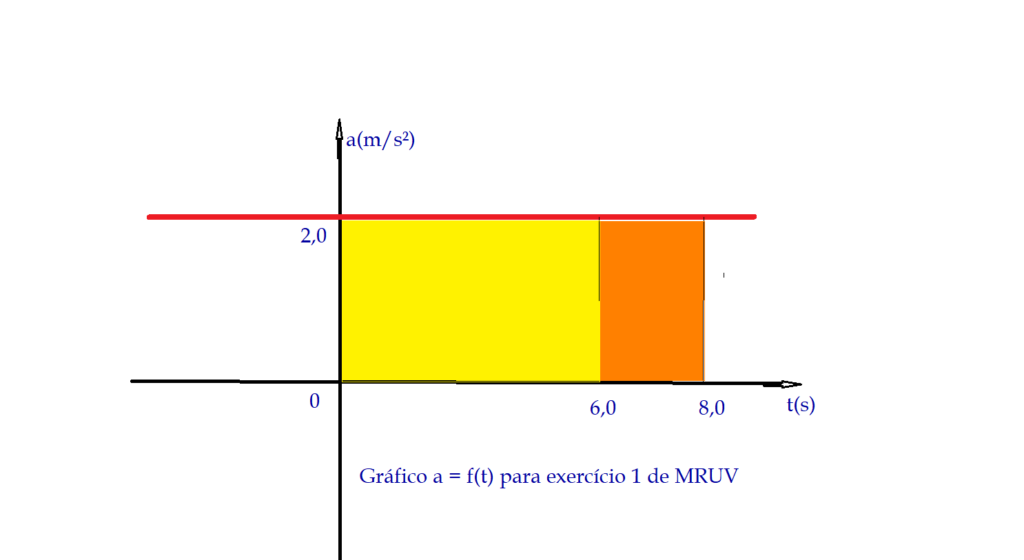
A representação gráfica da aceleração em função do tempo $\color{Blue}{a = f(t)}$, resulta em uma reta paralela ao eixo das abcissas ${t}$. Essa reta pode estar acima ou abaixo desse eixo, o que significa que a aceleração será ou positiva ${(+)}$ ou negativa ${(-)}$, conforme esteja acima ou abaixo do eixo.
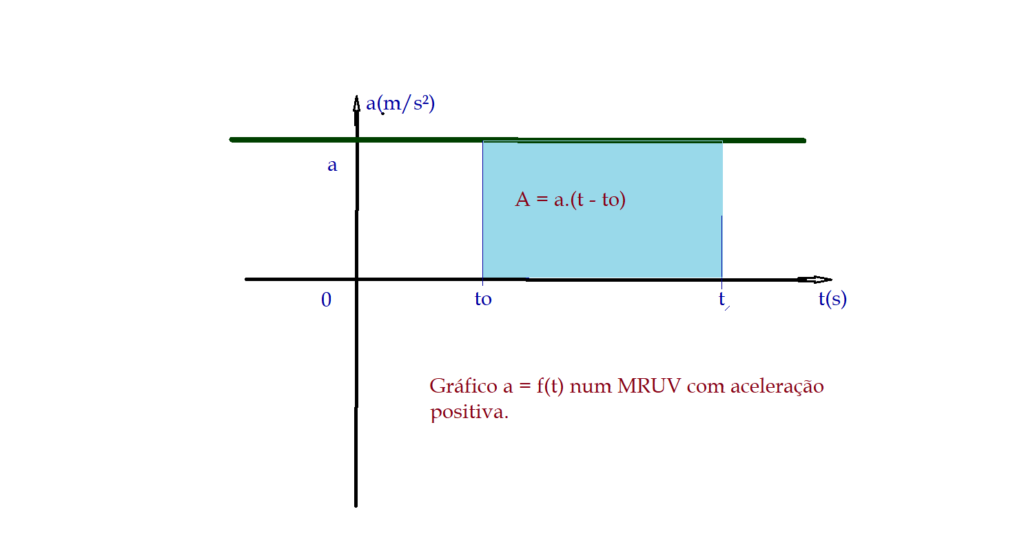
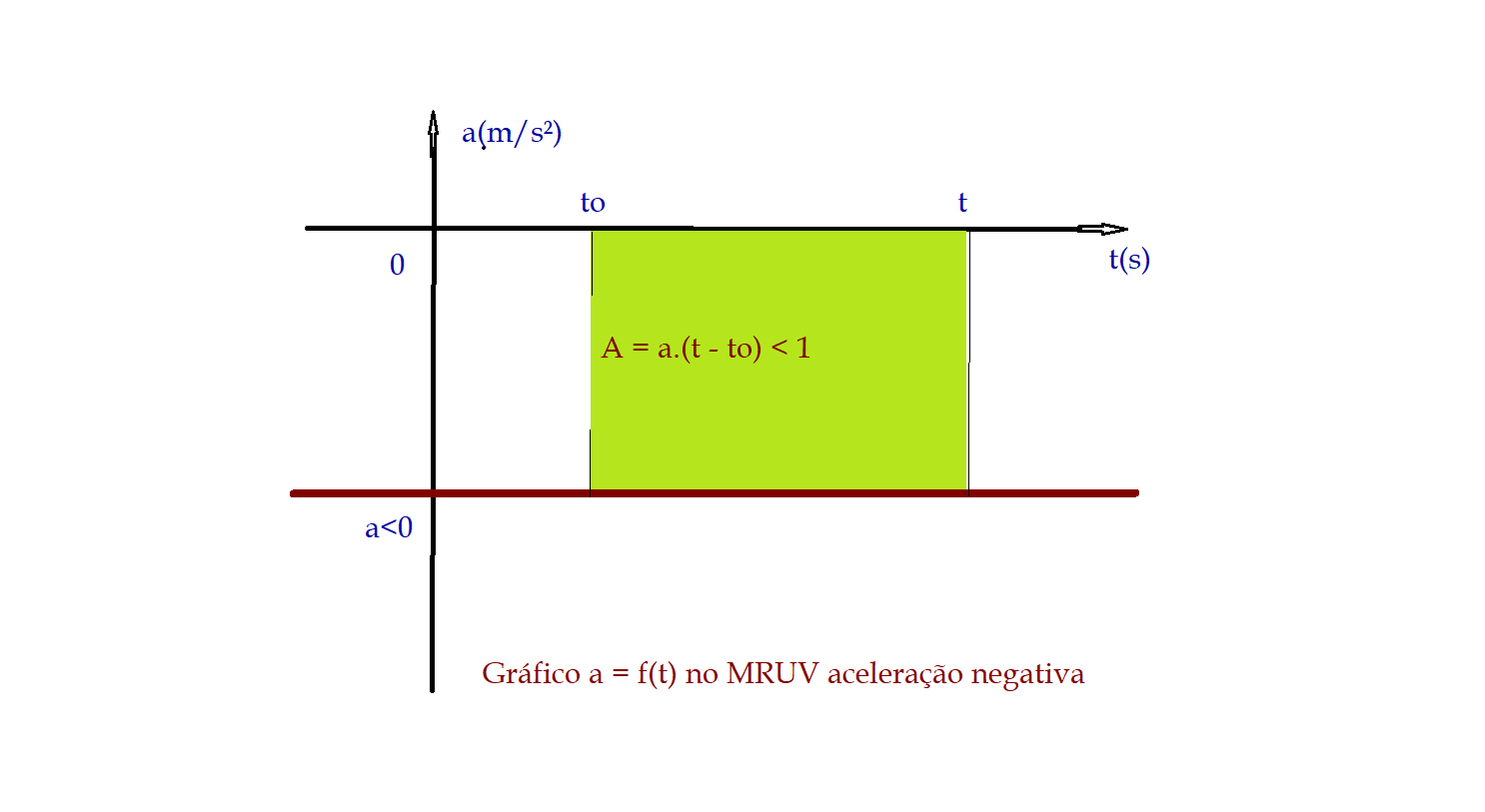
A área determinada por essa reta e o eixo, para um intervalo de tempo $\Delta{t}$, é igual à variação da velocidade $V – V_{0} =\Delta{V}$, ocorrida nesse intervalo. Se a variação for positiva ${+}$ o movimento será acelerado, se for negativa ${-}$ o movimento será retardado.
Unidades de aceleração.
No SI (Sistema Internacional de Unidades) e no sistema técnico (MKgfS):
$a = \frac{V}{t}$$\Leftrightarrow$$a = \frac{\frac{m}{s}}{s} = \frac{m}{s^{2}}$
No sistema CGS (centímetro, grama, segundo) pouco usado.
$a = \frac{V}{t}$$\Leftrightarrow$$a = \frac{\frac{cm}{s}}{s} = \frac{cm}{s^{2}}$
Exercícios resolvidos
- Um móvel tem velocidade $V_{0} = 7,0\,\frac{m}{s}$, no instante $t_{0} = 2,0\,s$. Se possui aceleração $a = 2,0\,\frac{m}{s^{2}}$, qual será sua velocidade no instante $t = 6,0\,s$? Em que instante sua velocidade será igual a $V= 23,0\, \frac{m}{s}$? Construa os gráficos $V = f(t)$ e $a = f(t)$, identificando onde o movimento é progressivo, retrógrado, acelerado ou retardado.
- $V = V_{0} + {a}\cdot\Delta{t}$
- $V_{0} = 7,0\, \frac{m}{s}$
- $a = 2,0\,\frac{m}{s^{2}}$
- $t_{0} = 2,0\,s$
- $t = 6,0\, s$$\Rightarrow$$v = ?$
- $V = 7,0 + {2,0}\cdot{6,0 – 2,0}$$\Leftrightarrow$$V = 7,0 + {2,0}\cdot{4,0}$
- $V = 7,0 + 8,0 = 15,0\, \frac{m}{s}$$\Leftrightarrow$$V = 15,0\,\frac{m}{s}$
- $V = 23,0\, \frac{m}{s}$$\Rightarrow$$t = ?$
- $23,0 = 7,0 + {2,0}\cdot{t – 2,0}$$\Leftrightarrow$$23,0 – 7,0 = {2,0}\cdot{t} – 4,0$
- ${2,0}\cdot{t} = 16,0 + 4,0$
- $t = \frac{20,0}{2,0}$$\Leftrightarrow$$t = 10,0\,s$
2. Um móvel tem velocidade inicial $V_{0} = -12,0\,\frac{m}{s}$, quando começa a sofrer uma aceleração em sentido contrário $a = 3,0\,\frac{m}{s^{2}}$. Pergunta-se:
a) depois de quanto tempo sua velocidade será nula $V = 0$?
- ${v_0 = -12,0\,m/s}$
- ${a = 3,0 m/s²}$
- ${v = 0}$ para ${t = ?}$
- ${v = v_0 + a\cdot {t}}$
- $0 = -12,0 + {3,0}\cdot{t}$$\Leftrightarrow$${-3,0}\cdot{t} = – 12,0$
- $t = \frac{-12,0}{- 3,0}$$\Leftrightarrow$$ t = 4,0\, s$
b) qual será sua velocidade no instante $t = 7,0\,s$ após o início da aceleração contrária?
- $V = V_{0}+ a\cdot{t}$
- $a = 3,0\, \frac{m}{s^{2}}$
- $V_{0} = -12,0\, \frac{m}{s}$
- $ t = 7,0\, s$$\Leftrightarrow$$V = ?$
- $V = – 12,0 + {3,0}\cdot {7,0}$$\Leftrightarrow$$V = -12,0 + 21,0 = 9,0\, \frac{m}{s}$
c)Em que instante sua velocidade será $V = 12,0\, \frac{m}{s}$
- $V = V_{0} + a\cdot{t}$
- $V_{0} = -12,0\,\frac{m}{s}$
- $a = 3,0\, \frac{m}{s^{2}}$
- $V = – 12,0\, \frac{m}{s}$$\Leftrightarrow$$t = ?$
- $12,0 = -12,0 + {3,0}\cdot {t}$$\Leftrightarrow$$12,0 + 12,0 = {3,0}\cdot {t}$
- $24,0 = {3,0}\cdot{t}$$\Leftrightarrow$$ t = \frac{24,0}{3,0}$
- $t = 8,0\,s$
d) após um tempo $t = 15,0\,s$, qual será a sua velocidade?
- $V = V_{0} + a\cdot{t}$
- $V_{0} = -12,0\, \frac{m}{s}$
- $a = 3,0\, \frac{m}{s^{2}}$
- $t = 15,0\, s$$\Rightarrow$$V = ?$
- $V = -12,0 + {3,0}\cdot{15,0}$$\Leftrightarrow$$V = – 12,0 + 45,0 = 33,0 \frac{m}{s}$
- $V = 33,0\, \frac{m}{s}$
e) em que intervalos dos itens anteriores o movimento é retardado e em quais é acelerado?
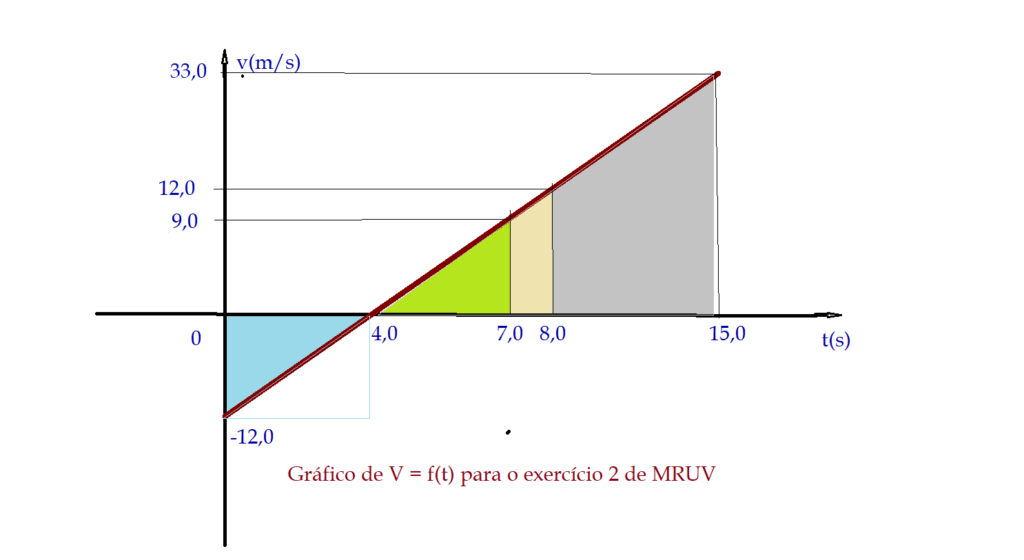
- os sinais da velocidade e aceleração são opostos até o instante $t = 4,0\,s$ e portanto o movimento é retardado. A partir do instante $t = 4,0\,s$ os sinais de velocidade e aceleração são iguais, portanto o movimento passa a ser acelerado.
- construir os gráficos $V = f(t)$ e $a = f(t)$, destacando as diferentes etapas do movimento.
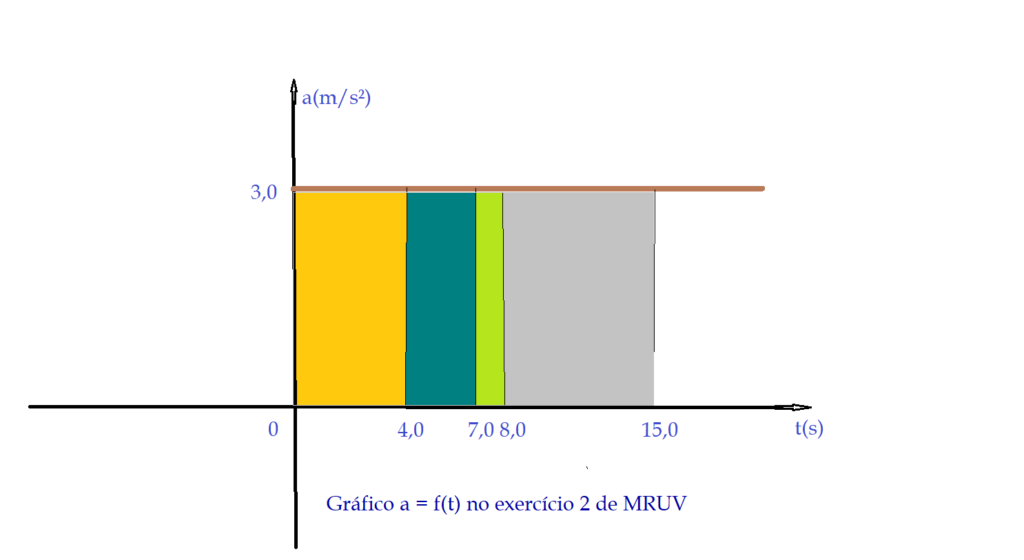
3) Um móvel tem aceleração constante $a = -5,0\,\frac{m}{s^{2}}$ e a velocidade no instante $t = 0$ é $V_{0} = 22,0\, \frac{m}{s}$. Determine: a) a velocidade que o móvel possui no instante $t = 7,0\, s$; b) o instante em que sua velocidade é igual a $ V = -22,0\,\frac{m}{s}$; c) a velocidade do móvel no instante $t = 12,0\,s$; d) represente graficamente $V = f(t)$ e $a = f(t)$, destacando os intervalos em que o movimento é progressivo, retrógrado, acelerado e retardado.
- a)$a = – 5,0\frac{m}{s^{2}}$
- $V_{0} = 22,0\,\frac{m}{s}$, para $t = 0\,s$
- $t = 7,0\,s$
- $V = V_{0} + a\cdot{t}$
- $V = {22,0} + {- 5,0}\cdot{7,0}$$\Leftrightarrow$$V = 22,0 – 35,0$
- $ V = – 13,0\, \frac{m}{s}$
- b) $V = -22,0\, \frac{m}{s}$$\Rightarrow$$t = ?$
- $-22,0 = 22,0 + {-5,0}\cdot{t}$
- ${-22,0 – 22,0} = {-5,0}\cdot{t}$
- ${5,0}\cdot{t} = {44,00}$
- ${t} =\frac{44,0}{5,0}$
- $t = 8,8\,s$
- c) $t = 12,0\,s$$\Rightarrow$$V = ?$
- $V = 22,0 +{-5,0}\cdot{12,0}$
- $V = 22,0 – 60,0$$\Leftrightarrow$$V = – 38,0\, \frac{m}{s}$
- d)
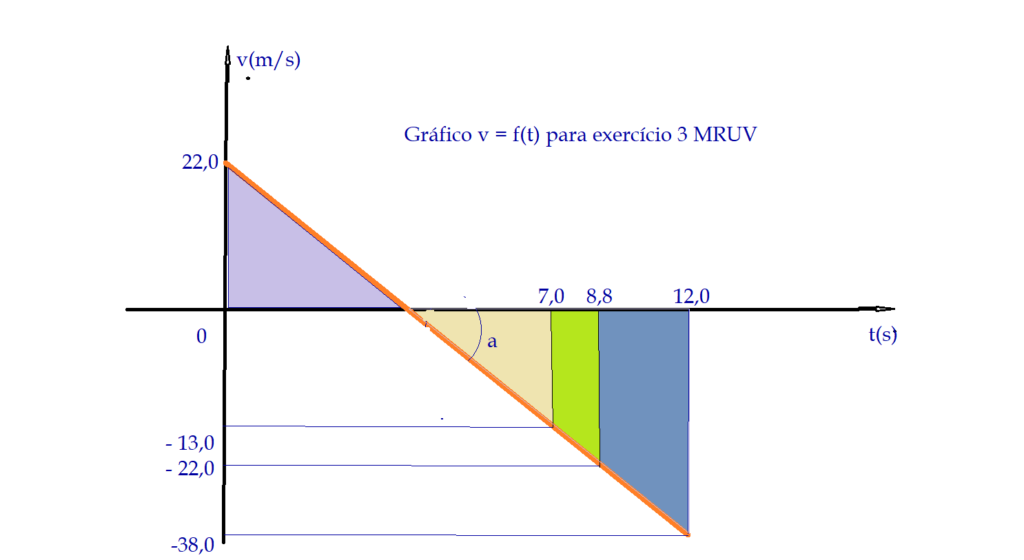
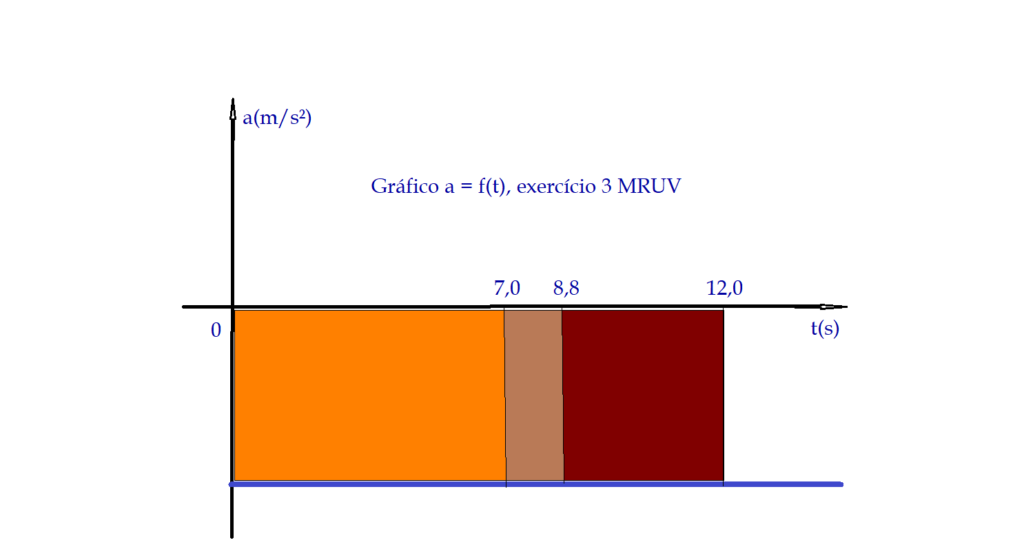
Exercícios para resolver.
- Sendo a velocidade de um móvel no instante $ t =0$ igual a $V_{0} = 4,0\,\frac{m}{s}$, com aceleração constante $a = – 3,0\,\frac{m}{s^{2}}$, determine: a) a velocidade no instante $ t = 9,0\, s$; b) o instante em que a velocidade se torna igual a $V = – 14,0\,\frac{m}{s}$; c) o instante em que o móvel para e inverte o sentido do movimento; d) faça os gráficos $V =f(t)$ e $a = f(t)$.
- Um móvel tem velocidade $V = – 15,0\,\frac{m}{s}$ e depois de um intervalo de $t = 6,0\, s$ a velocidade variou para $V = 9,0\,\frac{m}{s}$. a)Determine a aceleração desse movimento; b) o instante em que a velocidade será igual $V= 30,0\,\frac{m}{s}$; c) o instante em que ocorre a inversão do sentido de movimento; d) faça os gráficos $V =f(t)$ e $a = f(t)$.
- Com aceleração de $a = 2,0\,\frac{m}{s^{2}}$, um móvel parte do repouso e acelera até alcançar $V = 30,0\,\frac{m}{s}$. Nesse instante a aceleração se inverte e começa a desacelerar na mesma proporção. Em quanto tempo ele estará novamente em repouso? Continuando com a mesma aceleração contrária, com que velocidade ele chegará ao ponto de partida no início?
- Com velocidade inicial de $V = -8,0\,\frac{m}{s}$ e aceleração de $a = 2,0\,\frac{m}{s^{2}}$, um móvel percorre uma trajetória retilínea. Pergunta-se: a) em que instante ocorre a inversão do sentido do movimento? b) em que instante o móvel terá a velocidade $V = 8,0 \,\frac{m}{s}$; c) com que velocidade ele estará no instante $t = 12,0\,s$; d) em que instante ele terá uma velocidade igual a $V = 24,0\, \frac{m}{s}$? e) construa os gráficos $V =f(t)$ e $a = f(t)$, fazendo a análise dos diversos intervalos quanto a ser movimento progressivo, retrógrado, acelerado e retardado.
5. A velocidade de uma partícula varia de acordo com a função $v=4+8\times t$, em unidades SI. Pede-se
- a) A velocidade inicial da partícula;
- b) A aceleração da partícula;
- c) A velocidade da partícula no instante $t=2\,s$
- d) A variação de velocidade nos 4 primeiros segundos.
6. Um carro encontra-se parado em uma rodovia federal devido uma colisão de 2 veículos que estão impedindo o tráfego normal na pista. Imediatamente os 2 veículos são retirados da pista e a mesma é liberada. O condutor do carro que estava parado então acelera o carro (pisa no acelerador), depois de passados $5\,s$ o velocímetro do carro marca $30 \,km/h$. Qual foi a aceleração média do carro?
7. Um móvel desloca-se com velocidade inicial de $vo=20\,m/s$, quando inicia um processo de frenagem, com desaceleração de $a = -2,5\,m/s^{2}$. Determine o tempo necessário para que esse móvel inverta o seu sentido de movimento.
a) 8,0 s;
b) 50,0 s;
c) 5,0 s;
d) 10,0 s;
e) 12,5 s.
8. (FUVEST) Um veículo parte do repouso em movimento retilíneo e acelera com aceleração escalar constante e igual a $a=2,0\, m/s^{2}$. Pode-se dizer que sua velocidade escalar após 3,0 segundos, vale:
a) 6,0 m/s;
b) 6,0m/s;
c) 3,0 m/s;
d) 12 m/s;
e) 2,0 m/s.
Havendo dúvidas, faça contato comigo por um dos canais abaixo listados. Mesmo que as dúvidas sejam relativas a problemas do assunto vindos de sua escola ou curso que esteja fazendo, não precisa ficar na dúvida. Estarei disposto a auxiliar.
Curitiba, 12 de setembro de 2019.
www.facebook.com/livros.decioadams
Telefone: (41) 3019-4760
Celular e Whats App: (41) 99805-0732
