Física – Mecânica Dinâmica.
Trabalho Mecânico.
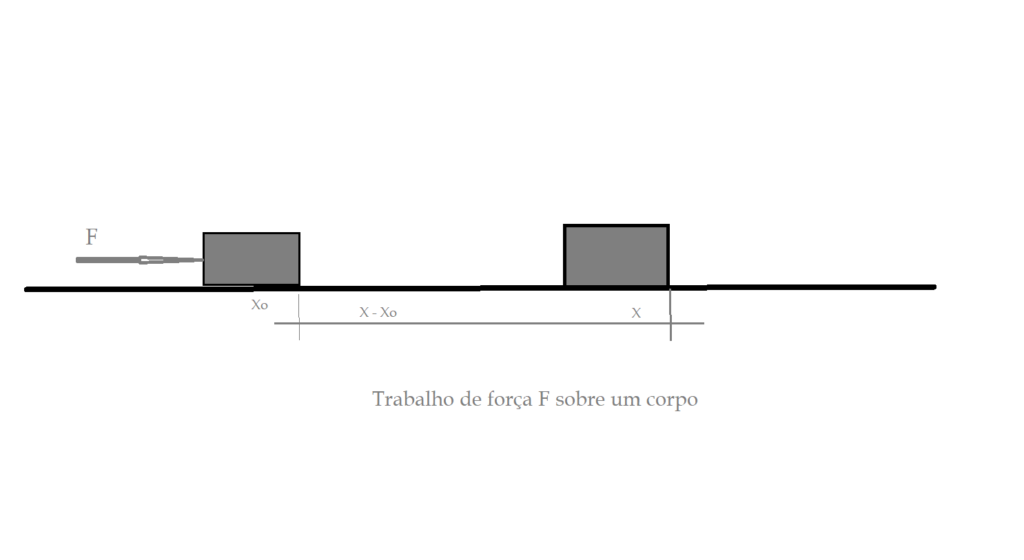
Uma força F, deslocando um móvel de uma distância X – Xo
O que quer dizer “trabalho mecânico”?
Será que nos referimos ao trabalho de um profissional mecânico, fazendo um serviço de manutenção em um veículo ou outra máquina qualquer, seja motorizada ou não?
Note que estamos dizendo “trabalho mecânico” e não “trabalho de mecânico”. Estamos falando de uma grandeza física, relacionada com a ação de uma força e o deslocamento do corpo sobre o qual é aplicada.
Denominamos Trabalho Mecânico ao ato de uma força, aplicada sobre um corpo e realizar um deslocamento do mesmo. Assim podemos inferir que essa grandeza depende de duas outras grandezas: a força e o deslocamento.
O trabalho realizado pela força, pode ser a favor do movimento, isto é, ter o mesmo sentido do deslocamento ou contrário, se ela agir contra o movimento. No primeiro caso ele é denominado Trabalho motor e no segundo, Trabalho resistente.
A força aplicada pode ser paralela à direção do deslocamento ou oblíqua. Por isso, a equação que nos dá o trabalho de uma força sobre um corpo, é o produto da intensidade da força, pelo módulo do deslocamento e pelo cosseno do ângulo entre a reta suporte da força e o deslocamento.
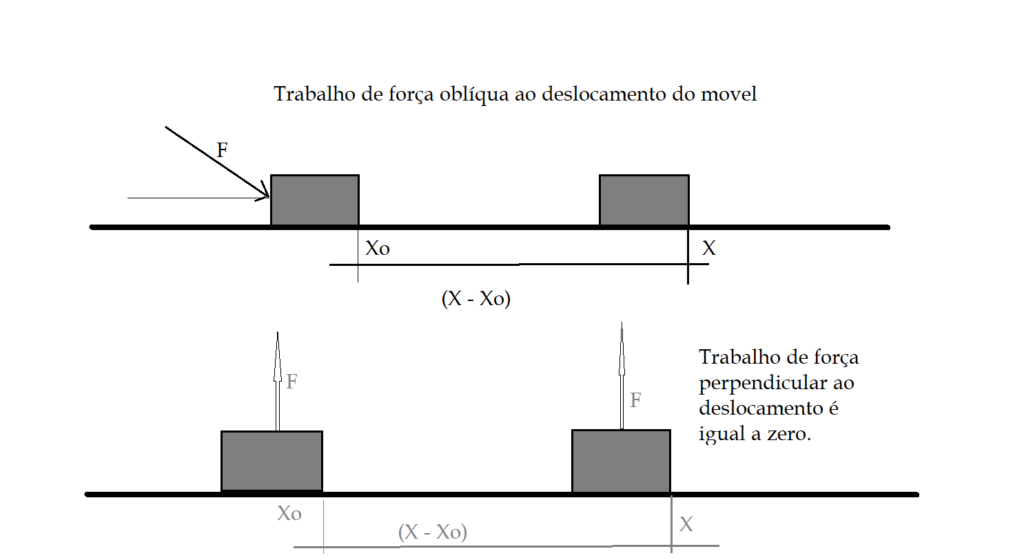
Sejam ${F}$ a força, ${\Delta{X}}$ o deslocamento e ${\alpha}$ o ângulo entre a direção da força ${F}$ e o deslocamento ${\Delta{X}}$. Podemos então escrever que:
${\tau= {F}\cdot{\Delta{X}}\cdot{cos{\alpha}}}$
Lembrando do círculo trigonométrico, podemos afirmar que o angulo ${\alpha}$ pode ser: ${\alpha = 0^0}$; ${0^0 < \alpha < {90^0}}$; ${\alpha = {90^0}}$; ${{90^0}<\alpha< {180^0}}$ e ${\alpha = {180^0}}$..
Por conseguinte teremos:
- ${\tau = {F}\cdot {\Delta{X}}\cdot{cos 0^0}}$ quando ${\alpha = 0^0}$
- ${\tau = {F}\cdot {\Delta{X}}\cdot{cos\alpha}}$, para ${0^0 < \alpha < {90^0}}$, nestes dois casos o trabalho será motor.
- ${\tau = {F}\cdot 0}$, quando ${\alpha = {90^0}}$$\Leftrightarrow$${\tau = 0}$
- ${\tau = {F}\cdot {\Delta{X}}\cdot{cos\alpha}}$, para ${{90^0}< \alpha < {180^0}}$
- ${\tau = {f}\cdot{\Delta{X}}\cdot{cos\alpha}}$, para ${\alpha = {180^0}}$
- Nestes dois últimos casos o trabalho será resistente, pois o cosseno do ângulo é negativo.
Quanto maior for a intensidade da força, o deslocamento e o cosseno do ângulo, maior será o módulo do trabalho. Sempre que definimos uma nova grandeza física, é necessário estabelecer as unidades, que variam para cada sistema de unidades utilizado.
No SI (Sistema Internacional de Unidades), temos que:
- a força é medida em newton ${(N)}$
- o deslocamento em metro ${(m)}$
- o cosseno é um número adimensional (não usa unidades)
- Isso nos dá que o trabalho vai ser medido em ${N.m}$. Esta unidade,em homenagem ao físico frances Charles Prescot Joule, foi batizada com seu nome. Portanto ${N.m = 1joule = 1\,J}$
No sistema técnico ou técnico métrico:
- a força é medida em quilogramaforça ${kgf}$;
- o deslocamento em metro ${m}$;
- o cosseno como vimos não tem unidade.
- daí o trabalho nesse sistema passa a ser ${kgf.m}$ ou ${kgm}$.
No sistema CGS (em desuso), temos:
- força medida em dina ${dyn}$;
- deslocamento medido em centímetros ${cm}$;
- o trabalho será ${dyn.cm}$ ou ${erg}$
Representação gráfica $F=f(\Delta x)$
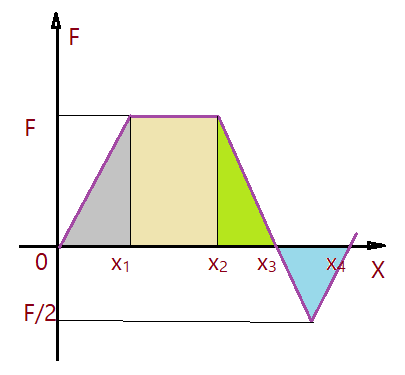
Podemos representar a força resultante que atua num corpo em função do deslocamento ao estudarmos o trabalho realizado. Vejamos um exemplo.
Se a intensidade da força $F$ fosse constante ao longo de todo deslocamento, bastaria determinar a área de um retângulo e teríamos o trabalho realizado. Como temos etapas diferentes, teremos necessidade de calcular em partes.
$\tau_{1} = \frac{F\times (x_{1} – 0)}{2}$$\Rightarrow$ área de triângulo.
$\tau_{2} = F\times (x_{2} – x_{1})$$\Rightarrow$ área do retângulo.
$\tau_{3} = \frac{F\times(x_{3} – x_{2})}{2}$$\Rightarrow$ área do triângulo.
$\tau_{4} = \frac{\frac{- F}{2}\times (x_{4} -x_{3})}{2}$$\Rightarrow$ área do triângulo.
Potência desenvolvida por um sistema
Uma pergunta que facilmente você se fará:
- Como fica o tempo gasto na realização de uma determinada quantidade de trabalho?
É disso que iremos falar agora. Basta dividir o trabalho pelo tempo gasto em realizá-lo para obtermos uma nova grandeza: a Potência.
$$\color{Navy}{P = \frac{\tau}{\Delta t}}$$
Isso está relacionado com todo tipo de máquina. Um automóvel, motocicleta, um caminhão, trator e muitas outras. Um motor de baixa potência é capaz de levar uma carga grande até o alto de um morro, desde que esteja acoplado a um sistema de transmissão adequado. Certamente irá demorar muito mais do que um motor mais potente. As primeiras máquinas motrizes que o homem fabricou eram de baixa potência e ainda carregavam em seu desfavor o baixo rendimento. Com o passar do tempo, a demanda por potências mais elevadas, também trouxe o aumento de rendimento. Um motor de alto rendimento, consegue converter em trabalho útil um percentual mais elevado da energia que consome em seu funcionamento.
Unidades de potência
No SI, temos: $\tau = joule (J)$ e $t = s$. Logo:
$$\color{Navy}{P = \frac{J}{s} = watt(W)}$$
Obs.: Essa unidade é uma homenagem ao físico e pesquisador James Watt.
No sistema técnico ou MKgfS: $\tau = kgm$ e $t = s$.
$$\color{Navy}{P = kgm/s}$$
No CGS, temos: $\tau = erg$ e $t = s$.
$$\color{Navy}{P= erg/s}$$
Rendimento
O rendimento, obtém-se dividindo a potência útil, pela potência total. É adimensional e nos aponta a fração ou percentual de energia (Potência) é convertido em trabalho útil.
$$\color{Navy}{\eta =\frac{P_{u}}{P_{t}}}$$
Em percentual:
$$\color{Navy}{\eta = 100\times\left(\frac{P_{u}}{P_{t}}\right)\%}$$
Podemos escrever: $P_{t} = P_{u} + P_{d}$$\Leftrightarrow$$P_{u} = P_{t} – P_{d}$
Substituindo na primeira equação:
$\eta = \frac{P_{t} – P_{d}}{P_{t}}$$\Leftrightarrow$$\eta = 1 – \frac{P_{d}}{P_{t}}$
Em percentual:
$$\color{Navy}{\eta = 100\left(1 – \frac{P_{d}}{P_{t}}\right)\%}$$
Sempre é bom exercitar. Vamos resolver uns exemplos.
- Se uma força de ${F = 50,0\,N}$ é aplicada numa direção paralela ao deslocamento de um corpo que percorre uma distância igual a ${{\Delta{X}} = 15,0\,m}$ sob ação da mesma, qual será o trabalho realizado ao final?
- ${F = 50,0\,N}$
- ${\Delta {X} = 15,0\,m}$
- ${\alpha = {0^0}}$
- ${cos 0^0 = 1}$
- ${\tau= {F}\cdot{\Delta{X}}\cdot{\alpha}}$
- então
- ${\tau={50,0}\cdot{15,0}\cdot {1,0}}$
- ${\tau =750,0\,J}$
- Note que se a força agisse no sentido contrário ao movimento, o ângulo ${\alpha = 180^0}$
- ${cos (180^0) = – 1,0}$
- Por isso o trabalho teria o mesmo módulo, porém negativo ou seja trabalho resistente.
2. Uma força ${F = 200,0\,kgf}$, atua sobre um corpo numa direção que forma um ângulo de ${\alpha = 120^0}$ com a direção do deslocamento. Se o deslocamento total é de ${\Delta{X} = 0,35\,m}$, qual é o trabalho realizado por essa força?
- ${F = 200,0\,kgf}$
- ${\Delta{X} = 0,35\,m}$
- ${\alpha = 120^0}$
- Então ${\tau={F}\cdot{\Delta {X}}\cdot {cos{\alpha}}}$
- ${\tau ={200,0}\cdot {0,35}\cdot {(-0,5)}}$
- ${\tau={ 70,0}\cdot{(-0,5)}}$
- ${\tau = – 35,0}$
- O trabalho é resistente.
3. Uma força de ${F = 300,0\,N}$ realiza sobre um corpo um trabalho de
${\tau = 1050,0\,J}$. Se o ângulo entre a direção da força e o deslocamento é de ${\alpha = 60^0}$, quanto mede o deslocamento que o corpo realiza?
- ${F = 300,0\,N}$
- ${\tau = 1050,0\,J}$
- ${\alpha = 60^0}$
- ${\Delta{X} = ?}$
- ${\tau = {F}\cdot\Delta{X}\cdot{cos60^0}}$
- ${1050,0 = {300}\cdot{\Delta{X}}\cdot {0,5}}$
- ${1050,0 = 150\cdot{\Delta{X}}}$
- ${{{1050}\over{150}} = \Delta{X}}$
- ${\Delta{X} = 7,0\,m}$
4) Uma pessoa levanta uma mala de ${20,0\,kg}$, até uma altura de ${50,0\,cm}$ e depois a carrega por uma distância de ${50,0\,m}$. Se a aceleração da gravidade for igual a ${g = 10,0\,m/s²}$, pergunta-se:
a) qual foi o trabalho realizado ao levantar a mala do chão até a altura de ${50,0\,cm}$?
- A força necessária para levantar a mala é um valor ligeiramente maior do que o peso e consideraremos neste caso igual ao peso da mala.
- ${P = m\cdot {g}}$
- ${g = 10,0\,m/s²}$ (ao fazer essa aproximação estaremos cometendo um ligeiro erro, geralmente considerado insignificante.
- Então ${F = m\cdot{g}}$
- As forças ${F}$ e ${P}$ tem a mesma direção e sentidos contrários, mas nesse caso o deslocamento e a força que o produz tem o mesmo sentido, o que mostra que o ângulo ${\alpha = 0^0}$
- ${\tau = {20,0}\cdot{10,0}\cdot {0,50}\cdot {cos 0^0}}$
- ${\tau = {200,0}\cdot {0,50}\cdot {1}}$
- ${\tau = 100\,J}$
b) Qual é o trabalho realizado durante a caminhada de ${50,0\,m}$, levando a mala sempre na mesma altura?
- ${\Delta{X}}$ é um deslocamento horizontal.
- ${F}$$\Rightarrow$ a força que a pessoa faz segurando a mala tem direção vertical e portanto o ângulo ${\alpha = 90^{0}}$
- ${\tau = {F}\cdot{\Delta{x}}\cdot {cos {90^0}}}$
- ${\tau = {20,0}\cdot {10,0}\cdot 0}$
- ${\tau = 0}$$\Rightarrow$ o trabalho neste deslocamento é nulo.
c) qual será o trabalho ao recolocar a mala no chão?
- Temos agora a situação inversa do momento de levantar a mala. O movimento é vertical, mas em sentido oposto ao da força aplicada, supondo-se que a mala seja colocada suavemente, não deixada cair.
- Então o ângulo entre a força aplicada e o deslocamento é $\alpha =(180^{0})$
- ${\tau = {F}\cdot{\Delta{X}}\cdot {cos{180^0}}}$
- ${\tau = {20,0}\cdot{10,0}\cdot{0,50}\cdot {(-1,0)}}$
- ${\tau = {200,0}\cdot {(- 0,50)}}$
- ${\tau = – 100,00\,J}$$\Rightarrow$gora o trabalho realizado pela pessoa é resistente.
05. A potência disponível em uma queda d’água é de 800 kW. Qual é a potência útil que se pode obter com essa queda d’água se nela for utilizada uma máquina hidráulica de rendimento igual a 50%?
Dados:$P_{t} = 800kW$, $\eta = 50\%$
$$\color{Maroon}{\eta = 100\times\left(\frac{P_{u}}{P_{t}}\right)\%}$$
$50 = 100\times\left(\frac{P_{u}}{800}\right)$$\Leftrightarrow$$P_{u} = \frac{50\times 800}{100}= 400kW$
$$\color{Navy}{P_{u} = 400\,kW}$$
06. Sobre um carro de grande porte que se movimenta com velocidade constante de 30 m/s é exercida uma força de 1000 N. Sabendo que seu rendimento é de 20%, determine, aproximadamente, a potência consumida pelo motor desse carro em HP (Horse power).
Dado: $1 HP = 746\,w$, $\eta = 20\%$. $v =30\,m/s$ e $F=1000\,N$
Temos que: $P = \frac{\tau}{\Delta t} = \frac{F\times \Delta x}{\Delta t}$
Isso nos dá que: $P_{u} = \frac{N\times m}{s}$
Assim: $P_{u} = \frac{1000\times 30}{1} = 30000\,W$
$\eta = 100\times\frac{P_{u}}{P_{t}}$$\Leftrightarrow$$P_{t}= 100\times\frac{30000}{20} = 150000\,W = 150\,kW$
$1\,HP = 746 W$
$x = 150000W$
$x = \frac{150000}{746} = 201,07\,HP$
A potência do motor é 201,07 HP. Via de regra seria considerado como sendo $P = 200\,HP.
Exercícios para resolver
- Calcule o trabalho realizado por uma força de ${F =135,0\,kgf}$, atuando numa direção de ${\alpha = 30^0}$, em relação a trajetória horizontal de um corpo, que se move por uma distância de ${\Delta{X} = 7,0\,m}$
- Um móvel desloca-se do ponto ${X_0 = 5,0\,m}$ até o ponto ${X = 17,0\, m}$, atuando numa direção paralela ao deslocamento, realizando um trabalho de ${\tau =1020,0\,J}. Qual é a intensidade dessa força?
- Uma força ${F = 40,0 N}$ atua numa direção de ${\alpha = 135^0}$ em relação à trajetória de um corpo, que percorre a distância ${\Delta {X} = 8,0\,m}$ até parar. Qual foi o trabalho realizado pela força? Foi trabalho motor ou resistente?
- Uma força ${F}$ atua sobre um corpo que se desloca em uma trajetória horizontal de uma distância de ${\Delta {X} = 23,0\,m}$, realizando um trabalho ${\tau = 1035,0\,J}$. Se o ângulo que a força forma com a trajetória é ${\alpha = 60^0}$, qual é a intensidade da força?
- Uma força de ${F = 200,0\,dyn}$, atua sobre um corpo que percorre uma distância horizontal de ${\Delta{X} = 75,0\,cm}$. Sendo o ângulo entre a força e a trajetória igual a ${\alpha = 180^0}$, qual é o trabalho realizado pela força?
- Um corpo recebe um trabalho mecânico de ${\tau = 1500,0\,erg}$, ao deslocar-se de uma distância de ${\Delta{X} = 30,0\,cm}$, sob ação de uma força ${F}$, que atua num ângulo de ${\alpha = 30^0}$ com a trajetória. Qual é a intensidade da força aplicada?
- Um móvel, em trajetória retilínea, recebe um trabalho de ${\tau = 2750,0\,kgm}$, durante um deslocamento de ${\Delta{X} = 50,0\,m}$. Se o trabalho é realizado por uma força que atua numa direção de ${\alpha = {45^0}}$ com a trajetória, qual é a intensidade da força motora?
- Uma força de ${F =170,0\,kgf}$, atuando paralelamente à trajetória de um móvel que se desloca de uma distância de ${\Delta{X} = 22,0\,m}$. Qual é o trabalho realizado?
- Um móvel desloca-se de um ponto A até um ponto B, em trajetória retilínea, sob a ação de uma força de ${F = 300,0\,kgf}$. Esta força atua numa direção de ${\alpha = 60^0}$ com a trajetória e realiza um trabalho de ${\tau = 900,0\,kgm}$. Qual é o deslocamento realizado pelo corpo?
- Um móvel é freado até parar, pela ação de uma força de ${F = 500,0\, N}$. Se o trabalho realizado pela força é de ${\tau = 3500,0\,J}$ e o deslocamento é de ${\Delta{X} = 7,0\,m}$, qual é o ângulo de ação da força sobre o móvel?
- Um móvel sofre um deslocamento ${\Delta{X} = 45,0\,m}$, sob a ação da força ${F = 300,0\,kgf}$, atuando na direção de ${\alpha = 45^0}$ em relação à trajetória. Qual é o valor do trabalho realizado pela força? Este trabalho é motor ou resistente?
- Um guindaste suspende um conteiner de massa igual a ${6,0\cdot {10^4}\,kg}$, até uma altura de ${h = {30,0}\,m}$. Supondo que o movimento de elevação é feito na vertical e que a aceleração da gravidade é ${g = {10,0}\,m/s^2}$, o guindaste é deslocado depois horizontalmente por uma distância ${\Delta{X} = {35,0}\,m}$ até o ponto em que será baixado para o convés do navio, situado ${{20,0}\,m}$ abaixo. Determine: a) o trabalho desenvolvido durante a elevação do conteiner; b) o trabalho durante o deslocamento horizontal, sabendo que a força de tração aplicada foi ${F = {9,0}\cdot{10^4}\,N}$; c) o trabalho resistente necessário para depositar o conteiner suavemente na superfície do convés do navio cargueiro.
13. (VUNESP) – Os dragsters são veículos que, acelerando uniformemente, chegam a atingir velocidade de $v=360\, km/h$ em pistas planas e retas de $\Delta x = 400\,m$ de comprimento. Um dragster de $m = 600\,Kg$ de massa, que atinja essa marca, desenvolverá uma potência média, em $cv$ (cavalo-vapor), de, aproximadamente:
Dado: $1\,cv = 735\,w$
( )a) 500;
( )b) 510;
( )c) 1000;
( )d) 1020;
( )e) 1750.
14. (UFPE) – Um automóvel se desloca em uma estrada plana e reta com velocidade constante $v = 80\,km/h$. A potência do motor do automóvel é $P = 25\,kW$. Supondo que todas as forças que atuam no automóvel sejam constantes, calcule o módulo da força de atrito total em unidades SI.
( )a) 1125;
( )b) 2250;
( )c) 3120;
( )d) 3200;
( )e) 4500.
15. (Unitau-SP) – Um halterofilista eleva um conjunto de barra e anilhas cuja massa total é de $m = 200\, k$g. Inicialmente, o conjunto estava em equilíbrio estático, apoiado sobre a superfície do piso. O halterofilista eleva o conjunto até uma altura de dois metros em relação ao piso. O movimento de elevação do conjunto foi realizado em um intervalo de tempo de quatro segundos. Considere o módulo da aceleração gravitacional terrestre como $g = 10\,m/s^{2}$. A potência média gasta pelo halterofilista para elevar o conjunto de barra e halteres foi de:
( )a) $0,5\times 10^{3}\,W$;
( )b) $10^{2}\,W$;
( )c) $10^{3}\,W$;
( )d) $2\times 10^{3}\,W$;
( )e) $4\times10^{3}\,W$.
16. (Enem) – A usina de Itaipu é uma das maiores hidrelétricas do mundo em geração de energia. Com 20 unidades geradoras e $P=14 000\,MW$ de potência total instalada, ela apresenta uma queda de $h=118,4\,m$ e vazão nominal de $\phi = 690\,m^{3}/s$ por unidade geradora. O cálculo da potência teórica leva em conta a altura da massa de água represada pela barragem, a gravidade local ($g = 10\,m/s^{2}$) e a densidade da água ($\mu =1 000 kg/m^{3}$). A diferença entre a potência teórica e a instalada é a potência não aproveitada.
Disponível em: www.itaipu.gov.br.
Qual é a potência, em MW, não aproveitada em cada unidade geradora de Itaipu?
( )a) 0;
( )b) 1,18;
( )c) 116,96;
( )d) 816,96;
( )e) 13 183,04.
17. Um objeto de $m=200\,kg$ é acelerado a $a=4\,m/s^{2}$ sob ação de uma força $F$. Determine a distância deslocada pelo objeto sob ação dessa força sabendo que a energia transferida para ele foi de $9,6 kJ$.
( )a) 8 m;
( )b) 10 m;
( )c) 12 m;
( )d) 13 m;
( )e) 14 m.
18. Um homem aplica uma força sobre um objeto de $m=20 \,g,$ empurrando-o por uma distância de $\Delta x =200\,mm$. Sabendo que o trabalho realizado pelo homem foi de $\tau =8\,kJ$, determine a aceleração, em $m/s^{2}$, do objeto durante o movimento. Considere que a força é paralela à direção de deslocamento da caixa.
( )a) 1;
( )b) 2;
( )c) 3;
( )d) 2,5;
( )e) 1,5.
19. (FCM-PB) – Em uma cachoeira aproveitada para mover uma roda d’água, a potência disponível é de $P_{t}=300\,kW$. Qual a potência útil para essa roda d’água cujo rendimento é de $\eta=50\%$?
( )a) 150 kW;
( )b) 450 kW;
( )c) 50 kW;
( )d) 100 kW;
( )e) 200 kW.
20. (Uncisal) – No filme “De volta para o futuro” (Universal Pictures, USA, 1985), o protagonista cria uma máquina do tempo utilizando um automóvel modelo DeLorean DMC 1981. Para isso, o seu motor foi modificado para que fosse capaz de produzir uma potência de $P=1,21\,GW$. Supondo o rendimento do motor de $\eta=50\%$, a massa do automóvel igual a $m=1.210\,kg$ e desprezando a resistência do ar, um DeLorean com uma potência de $P=1,21\,GW$ atingiria de $0\,a\,100\,Km/h$ ($100\,km/h\simeq 27\,m/s$) em um tempo de:
( )a) 223,1 μs;
( )b) 364,5 μs;
( )c) 441,0 μs;
( )d) 605,0 μs;
( )e) 729,0 μs.
21. Leia as seguintes afirmações a respeito das grandezas potência e rendimento.
I – O rendimento é resultado da razão entre a potência total disponível e a potência efetivamente utilizada.
II – Cavalo-vapor é uma unidade de medida de potência maior que a unidade horse-power.
III – Se uma máquina que possui rendimento de $\eta=40\%$ apresentar potência total de $P_{t}=500\,W$, a potência efetivamente utilizada será de $p_{u}=200\,W$.
Está correto o que se afirma em:
( )a) I e II;
( )b) II e III;
( )c) I e III;
( )d) Apenas I;
( )e) Apenas III.
22. Um homem empurra um objeto fazendo uma força de $F=100\,N$ por uma distância de $\Delta x = 25\, m$. Sabendo que o tempo gasto na execução da atividade foi de $\Delta t =50\,s$, determine a potência do homem.
( )a) 250 W;
( )b) 150 W;
( )c) 100 W;
( )d) 50 W;
( )e) 25 W.
23. (PUC Minas) – Considere um corpo sendo arrastado, com velocidade constante, sobre uma superfície horizontal onde o atrito não é desprezível. Considere as afirmações I, II e III a respeito da situação descrita:
I. O trabalho da força de atrito é nulo.
II. O trabalho da força peso é nulo.
III. A força que arrasta o corpo é nula.
A afirmação está INCORRETA em:
( )a) I, apenas;
( )b) II, apenas;
( )c)I e III, apenas;
( )d) I, II e III;
( )e) III, apenas.
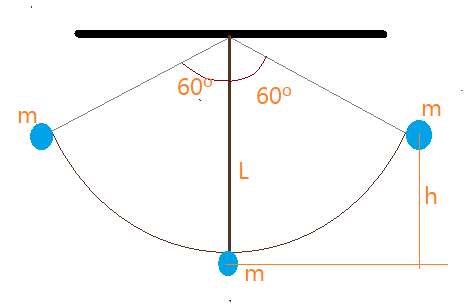
24. (UEL-PR) – Um pêndulo é constituído de uma esfera de massa $m =2,0\,kg$, presa a um fio de massa desprezível e comprimento $L =2,0\,m$, que pende do teto, conforme figura a seguir. O pêndulo oscila formando um ângulo máximo de $\alpha =60^{o}$ com a vertical.
Nessas condições, o trabalho realizado pela força de tração que o fio exerce sobre a esfera, entre a posição mais baixa e mais alta, em joules, vale:
( )a) 20;
( )b) 10;
( )c) zero;
( )d) -20;
( )e) -10.
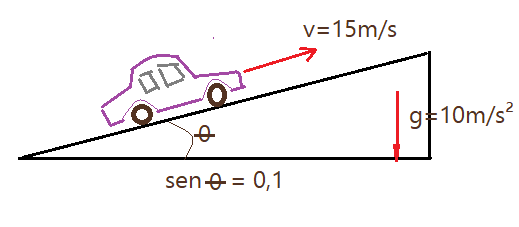
25. (FUVEST-SP) – Nos manuais de automóveis, a caracterização dos motores é feita em $cv$ (cavalo-vapor). Essa unidade, proposta no tempo das primeiras máquinas a vapor, correspondia à capacidade de um cavalo típico, que conseguia erguer, na vertical, com auxílio de uma roldana, um bloco de $m=75\,kg$, à velocidade de $v = 1\,m/s$. Para subir uma ladeira inclinada, como na figura, um carro de $m = 1 000\,kg$, mantendo uma velocidade constante de $v_{c}= 15\,m/s$ (54 km/h), desenvolve uma potência útil que, em $cv$, é, aproximadamente, de:
( )a) 20 cv;
( )b) 40 cv;
( )c) 50 cv;
( )d) 100 cv;
( )e) 150 cv.
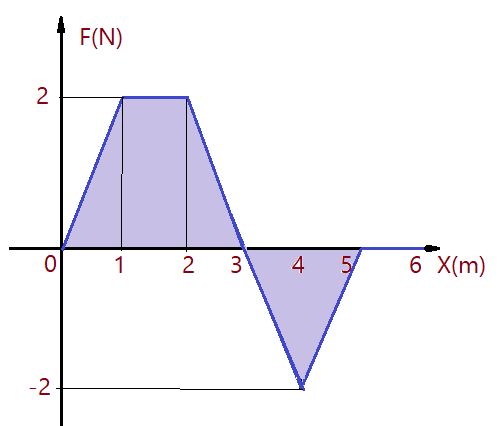
26. (UFSCar-SP) – Um bloco de $m=10\,kg$ movimenta-se em linha reta sobre uma mesa lisa, em posição horizontal, sob a ação de uma força variável que atua na mesma direção do movimento, conforme o gráfico a seguir. O trabalho realizado pela força quando o bloco se desloca da origem até o ponto $x = 6\,m$ é:
( )a) 1\,J;
( )b) 6\,J;
( )c) 4\,J;
( )d) zero;
( )e) 2\,J.
27. (UFMG–2007) – Antônio precisa elevar um bloco até uma altura $h$. Para isso, ele dispõe de uma roldana e de uma corda e imagina duas maneiras para realizar a tarefa,como mostrado nestas figuras:
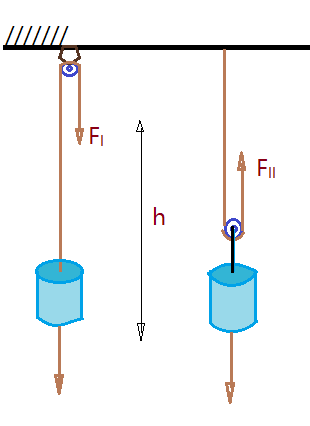
Despreze a massa da corda e a da roldana e considere que o bloco se move com velocidade constante. Sejam $F_{I}$ o módulo da força necessária para elevar o bloco e $T_{I}$ o trabalho realizado por essa força na situação mostrada na figura $I$. Na situação mostrada na figura $II$, essas grandezas são, respectivamente, $F_{II}$ e $T_{II}$.
Com base nessas informações, é CORRETO afirmar que:
( )a) $2F_{I} = F_{II}$ e $T_{I} = T_{II}$;
( )b) $F_{I} = 2F_{II}$ e $T_{I} = T_{II}$;
( )c) $2F_{I} = F_{II}$ e $2T_{I} = T_{II}$;
( )d) $F_{I} = 2F_{I}$I e $T_{I} = 2T_{II}$;
( )e)$F_{I} = F_{II}$ e $T_{I} = T_{II}$.
28. (UFMG–2006) – Marcos e Valério puxam, cada um, uma mala de mesma massa até uma altura h, com velocidade constante, como representado nas figuras a seguir.
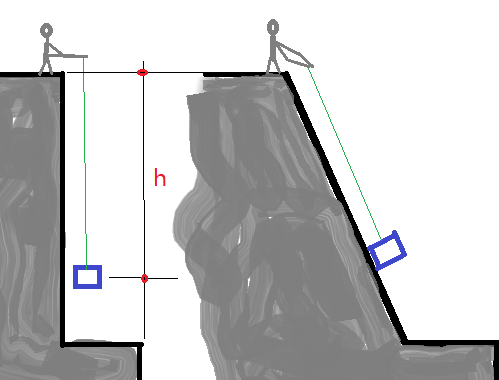
Marcos puxa sua mala verticalmente, enquanto Valério arrasta a sua sobre uma rampa. Ambos gastam o mesmo tempo nessa operação. Despreze as massas das cordas e qualquer tipo de atrito. Sejam $P_{M}$ e $P_{V}$ as potências e $T_{M}$ e $T_{V}$ os trabalhos realizados por, respectivamente, Marcos e Valério. Considerando-se essas informações, é CORRETO afirmar que:
( )a) $T_{M} = T_{V}$ e $P_{M} = P_{V}$;
( )b) $T_{M} > T_{V}$ e $P_{M} > P_{V}$;
( )c) $T_{M} = T_{V}$ e $P_{M} > P_{V}$;
( )d) $_{T}M < T_{V}$ e $P_{M} = P_{V}$;
( )e) $T_{M} <T_{V}$ e $P_{M} >P_{V}$.
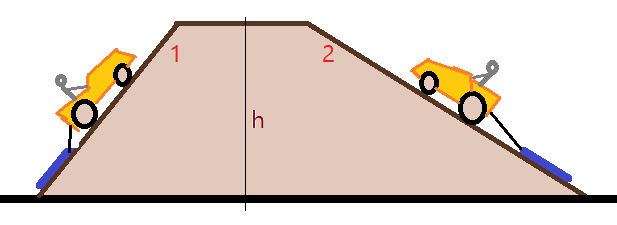
29. (UNESP–2009) – Suponha que os tratores 1 e 2 da figura arrastem toras de mesma massa pelas rampas correspondentes, elevando-as à mesma altura $h$. Sabe-se que ambos se movimentam com velocidades constantes e que o comprimento da rampa 2 é o dobro do comprimento da rampa 1.
Chamando de $\tau_{1}$ e $\tau_{2}$ os trabalhos realizados pela força gravitacional sobre essas toras, pode-se afirmar que:
( )a) $\tau_{1} = \tau_{2}$; $\tau_{1} > 0$ e $\tau_{2} < 0$;
( )b) $\tau_{1} = 2\tau_{2}$; $\tau_{1} < 0$ e $\tau_{2} > 0$;
( )c) $\tau_{1} = \tau_{2}$; $\tau_{1} < 0$ e $\tau_{2} < 0$;
( )d) $2\tau_{1} = \tau_{2}$: $\tau_{1} < 0$ e $\tau_{2} < 0$;
( )e) N.d.a.
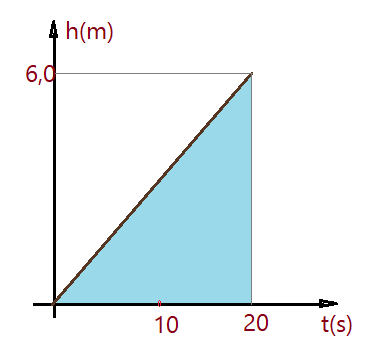
30. (FUVEST-SP) – Uma empilhadeira elétrica transporta do chão até uma prateleira, a $h =6\,m$ do chão, um pacote de $m=120\,kg$. O gráfico adiante ilustra a altura do pacote em função do tempo. A potência aplicada ao corpo pela empilhadeira é:
( )a) 120\,W;
( )b) 360\,W;
( )c) 720\,W;
( )d) 1200\,W;
( )e) 2400\,W.
31. (Unimontes-MG) – Um pequeno carrinho movimenta-se, sem atrito, numa montanha-russa. Sua energia potencial, que é máxima no ponto A, é medida a partir do nível do solo. O ponto B está num nível abaixo de A e acima de C. O trecho CD é retilíneo.
Considere as seguintes afirmativas a respeito da situação descrita:
I. O trabalho realizado pela força gravitacional sobre o carrinho é positivo no trajeto de A para B.
II. O trabalho realizado pela força gravitacional sobre o carrinho é positivo no trajeto de B para C.
III. O trabalho realizado pela força gravitacional sobre o carrinho é nulo no trajeto de C para D.
Estão CORRETAS as afirmativas:
( )a) I, II e III;
( )b) I e II, apenas;
( )c) I e III, apenas;
( )d) II e III, apenas;
( )e)III, apenas.
Havendo dúvidas, não hesite em contactar-me para esclarecimento, por meio de um dos canais que coloco abaixo.
Curitiba, 11 de setembro de 2019.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
