FI.ME.008-01 – Física – Mecânica, estática. Componentes ortogonais de um vetor.

By decioadams in Física 20 de outubro de 2017

Componentes ortogonais de um vetor.

Vimos que, para adicionarmos dois vetores com diferentes direções, podemos usar a fórmula geral deduzida no post anterior sobre o assunto. E se tivermos vários vetores, com diferentes direções?

Vejamos o exemplo da figura a seguir.

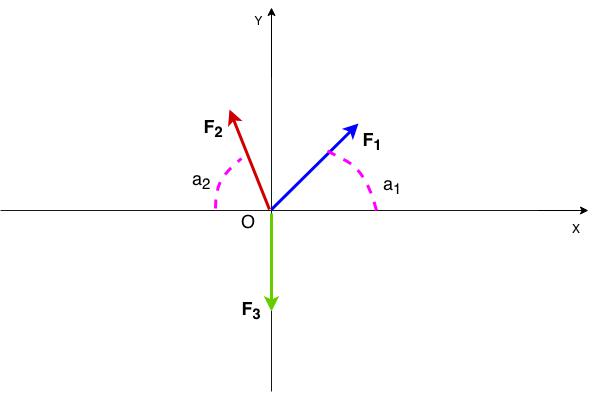
Vetores coplanares com diferentes direções. — Vetores coplanares, em direções diferentes, concorrentes no ponto de coordenadas $(0,0)$.

Temos três vetores, sendo dois com direções oblíquas em relação ao sistema de eixos $\color{Navy}{\widehat{ XOY}}$ e um terceiro coincidindo com o eixo $\color{Navy}{Y}$, no sentido negativo.
Assim como podemos encontrar o vetor soma de dois vetores perpendiculares entre si, podemos decompor um vetor dado, em dois vetores ortogonais, cuja soma seja igual ao vetor dado.

Vamos fazer essa operação para o vetor

$\color{Navy}{\vec{F_{1}}} $

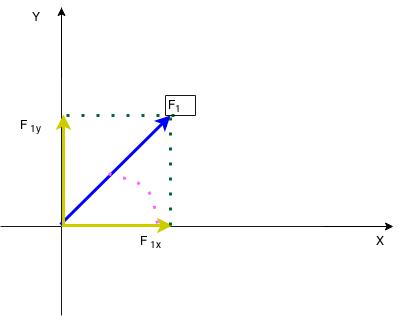
Vetor decomposto em seus componentes ortogonais (1) — Vetor $\color{Navy}{\vec{F_{1}}}$ decomposto em suas componentes ortogonais $\color{Navy}{\vec{F_{1x}}\land \vec{F_{1y}}} $

O vetor $\color{Navy}{\vec{F_{1}}}$ é na verdade o vetor soma das suas componentes nos eixos $\color{Navy}{\bar{OX}}$ e $\color{Navy}{\bar{OY}}$. Temos um retângulo, do qual o vetor é a diagonal. O angulo que ele forma com o eixo $\color{Navy}{\bar{OX}}$, permite que apliquemos a trigonometria e encontremos:

$\color{Navy}{cos {a_{1}} = \frac {\overline{F_{1x}}}{\overline{F_{1}}}}$
$\color{Navy}{cos {a_{1}}\cdot \overline{F_{1}} = \overline{F_{1x}}}$
$\color{Navy}{\overline{F_{1x}} = \overline{F_{1}}\cdot {cos{a_{1}}}}$

Temos a componente no eixo $\color{Navy}{\bar{X}}$. Vamos determinar a expressão da componente no eixo $\color{Navy}{\bar{Y}}$.

$\color{Navy}{sen {a_{1}} = \frac {\overline{F_{1y}}}{\overline{F_{1}}}}$
$\color{Navy}{sen {a_{1}}\cdot \overline{F_{1}} = \overline{F_{1y}}}$
$\color{Navy}{\overline{F_{1y}} = \overline{F_{1}} \cdot sen{a_{1}}}$

Podemos notar que a componente do vetor no eixo $X$ é igual ao produto do módulo do vetor pelo cosseno do ângulo entre o vetor e esse eixo.

A componente no eixo Y é igual ao produto do módulo do vetor pelo seno do ângulo que o vetor forma com o eixo X.

Se pegarmos o vetor $\color{Navy}{\vec{F_{2}}}$ e aplicarmos o mesmo procedimento, o ângulo entre o vetor e o eixo $\color{Navy}{\overline{OX}}$ é $\color{Navy}{a_{2}}$.

Vamos ter agora:

$ \color{Navy}{\overline{F_{2x}} = \overline{F_{2}} \cdot cos {a_{2}}}$
$ \color{Navy}{\overline{F_{2y}} = \overline{F_{2}}\cdot sen {a_{2}}}$

Já o terceiro vetor coincide com a direção do eixo $ \color{Navy}{Y}$ e por isso sua componente no eixo $ \color{Navy}{X}$ é nula. Diante disso podemos redesenhar o sistema de vetores, apenas com as componentes ortogonais. Veja como fica:

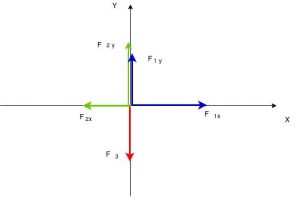
Sistema de vetores com suas componentes ortogonais. — Um sistema de vetores representado pelas componentes ortogonais dos vetores que formam o sistema.

O sistema agora é formado por componentes nas direções dos eixos ortogonais $\ \color{Navy}{\widehat{XOY}}$. A resolução, a partir daí, se reduz a determinar a resultante $ \color{Navy}{\vec{F_{x}} \land \vec{F_{y}}}$

Estas duas componentes formam um sistema de dois vetores ortogonais, onde será aplicado o Teorema de Pitágoras para obter o vetor soma, bem como a sua direção.

No eixo $ \color{Navy}{\overline{OX}}$, temos as componentes $ \color{Navy}{\overline{F_{1x}} \land \overline{F_{2x}}}$, que tem sentidos opostos. Em consequência a componente horizontal do sistema será:

$ \color{Navy}{\overline{F_{x}} =\overline{F_{1x}} – \overline{F_{2x}}}$

No eixo $ \color{Navy}{\overline{OY}}$, temos as componentes $ \color{Navy}{\overline{F_{1y}}, \overline{F_{2y}} \land \overline{F_{3}}} $

As duas primeiras têm sentido positivo e a última sentido negativo. A componente resultante será:

$ \color{Navy}{\overline{F_{y}} = \overline{F_{1y}} + \overline{F_{2y}} – \overline{F_{3}}}$

Como o sistema é ortogonal o vetor resultante será:

$ \color{Navy}{\bar{F^2} = \overline{F_{x}}^2 + \overline{F_{y}}^2 }$

O ângulo entre o vetor resultante e o eixo $ \color{Navy}{\bar{OX}}$, será dado pela expressão:

$ \color{Navy}{tg\beta = \frac {\overline{F_{y}}}{\overline{F_{x}}}}$

É portanto simples resolver a adição de um sistema com um número qualquer de componentes, utilizando o processo de decomposição desses componentes em componentes ortogonais. Sempre resultará no final um sistema com dois vetores ortogonais. Bastará aplicar o Teorema de Pitágoras e teremos o vetor soma. Dividindo a componente $\color{Navy}{Y}$ pela $\color{Navy}{X}$, obtemos a tangente do ângulo em relação ao eixo $\color{Navy}{X}$.

Este procedimento é extremamente útil em qualquer caso de grandezas vetoriais dentro de toda a disciplina de física.

Vejamos alguns exercícios.

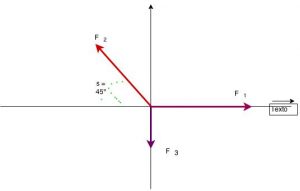
Exercício um — Forças concorrentes no ponto de coordenadas $(0,0)$.

1. Os vetores tem módulos de:
- $\color{Navy}{\vec{F_{1}} = 8 un}$
- $\color{Navy}{\vec{F_{2}} = 4\sqrt 2 un}$
- $\color{Navy}{\vec{F_{3}} = 5 un}$
- 2. Os vetores têm módulos de:
- $\color{Navy}{\vec{F_{1}} = 10 un}$
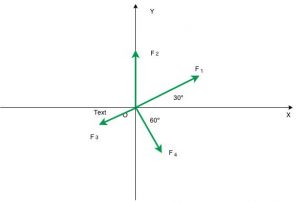
Exercício dois lI
- $\color{Navy}{\vec{F_{2}} = 8 un}$
- $\color{Navy}{\vec{F_{3}} = 4 un}$
- $\color{Navy}{\vec{F_{4}} = 6 un}$
Em caso de dúvidas sobre qualquer coisa use um dos meios listados abaixo para pedir auxílio. Não guarde sua dúvida para depois. Ela pode se tornar um grande problema, se não resolvida na hora em que ela surge.