FI.ME.007-01 – Física – Mecânica, estática. Operações com vetores.
Adição de vetores.
- A adição de vetores é importante, pois suas regras se aplicam à adição de quaisquer grandezas vetoriais, não importando o assunto em estudo. Começaremos pela adição de vetores de mesma direção.
- Vetores com a mesma direção e mesmo sentido. Basta transportar sobre uma mesma reta os vetores em sequência. A origem do segundo coincidirá com a extremidade do primeiro e assim por diante. O vetor soma terá orígem na orígem do primeiro vetor e extremidade na extremidade do último. Essa será a forma gráfica. O módulo do vetor resultante será igual a soma dos módulos dos vetores que foram somados.
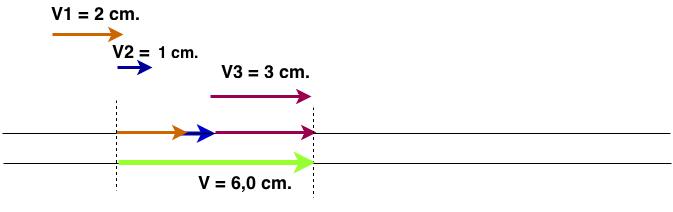
Podemos adicionar dois ou mais vetores e o procedimento será o mesmo.
- Vetores com a mesma direção e sentidos contrários. Transportamos os vetores sobre retas paralelas. O vetor soma terá origem na origem do primeiro vetor e extremidade na extremidade do último. Nesse caso o módulo do vetor soma será igual a diferença entre os módulos dos vetores somados.
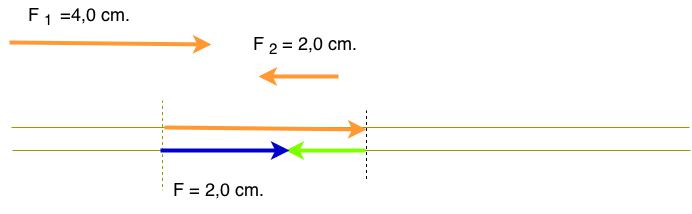
O módulo do vetor soma agora é a diferença entre os módulos dos vetores que foram somados.
- Vetores ortogonais. Traçamos os vetores a partir de uma origem comum, formando um ângulo reto. Pelas extremidades fazemos passar duas retas paralelas, completando um quadrilátero retângulo. A diagonal unindo a origem comum ao vértice oposto, será o vetor soma. Esse vetor soma estará na posição de hipotenusa de um triângulo retângulo, sendo possível calcular o seu módulo pelo uso do Teorema de Pitágoras.
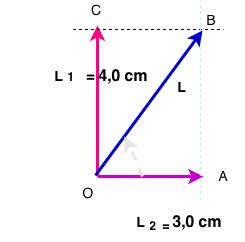
A diagonal $\color{Navy}{L}$, divide o retângulo $\color{Navy}{OABCO}$ em dois triângulos retângulos. No $\color{Navy}{\nabla{OABO}}$, $\color{Navy}{L}$ é a hipotenusa enquanto $\color{Navy}{L_1}$ e $\color{Navy}{L_2}$, são os catetos. O Teorema de Pitágoras nos permite escrever:
- $\color{Brown}{L^2 = {(L_1)}^2 + {(L_2)}^2}$
- $\color{Brown}{L^2 = (4,0)^2 + (3,0)^2}$
- $\color{Brown}{L^2 = 16,0 + 9,0 }$
- $\color{Brown}{L^2 = 25,0}$
- $\color{Brown}{L = \sqrt[2] {(25,0)}}$
- $\color{Brown}{L = 5,0}$
Temos determinado o módulo do vetor $\color{Maroon}{{L = 5,0}\,cm}$.
Falta determinarmos a direção, calculando a tangente do $\color{Brown}{\lt\widehat{BOA}}$.
- $\color{Navy}{tg\alpha = 4/3}$
- $\color{Navy}{tg\alpha = {4,0\over 3,0}}$
- $\color{Navy}{tg\alpha = {{L_1}\over{L_2}}}$
- $\color{Navy}{\alpha = arc tg{ 4/3}}$, ângulo do vetor $\color{Navy}{L}$ com o vetor $\color{Navy}{L_2}$.
- Que tal um pouco de exercícios?
- Determine o vetor resultante da soma de vetores. (Faça graficamente e o cálculo)
- Horizontais com $\color{Navy}{V_a = 6,0}$ cm e $\color{Navy}{V_b = 3,0}$ cm., com sentido para esquerda.
- Um vetor $\color{Navy}{F_n = 7,0}$ cm, horizontal para direita e $\color{Navy}{F_m = 5,0}$ cm, para esquerda.
- Um vetor $\color{Navy}{N_i = 3,0}$ cm, $\color{Navy}{N_j = 5,0}$ cm, para direita e $\color{Navy}{N_n = 4,0}$ cm, para esquerda.
- Um vetor $\color{Navy}{V_i = 9,0}$ cm, $\color{Navy}{V_j = 3,0}$ cm e $\color{Navy}{V_n = 5,0}$ cm, todos da esquerda para direita.
- Determine o módulo e a direção do vetor soma de dois vetores $\color{Navy}{V_i = 6,0}$ cm e $\color{Navy}{V_j = 8,0}$ cm, sendo $\color{Navy}{V_i}$, vertical e $\color{Navy}{V_j}$ horizontal. Determine o valor calculado e faça o gráfico.
Obs.: Em caso de dúvidas, faça contato comigo por um dos canais listados abaixo, para sanar suas dificuldades.
Curitiba, 16 de março de 2015 (.Atualizado em 28 de julho de 2016).
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
