Adição de vetores oblíquos.

• Já vimos como adicionar vetores de mesma direção e sentido, mesma direção e sentidos opostos, vetores ortogonais, onde a solução é usar o velho conhecido Teorema de Pitágoras.

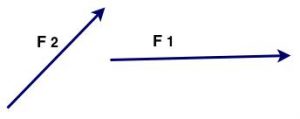
Podemos observar que as retas que contém os segmentos formadores dos vetores $\color{Navy}{\vec{F_1}}$ e $\color{Navy}{\vec{F_2}}$, tem um ponto em comum, isto é se interceptam em um ponto que denominaremos de O (origem) ou ponto de aplicação.

Para iniciar o raciocínio, vamos traspor os esses vetores sobre as suas retas suporte a partir do ponto de interseção O, formando os lados de um ângulo $\lt \widehat{AOC}$, com vértice em O. Isso é considerado como um “deslizamento” do vetor sobre a própria reta suporte ou retas paralelas, até a coincidência das origens.

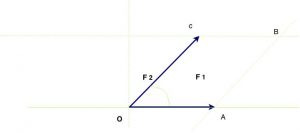
Depois traçamos duas retas paralelas as retas originais passando pelas extremidades A e C dos vetores. Essas se interceptam no ponto B, o vértice do paralelogramo $\widehat{OABCO}$.

Unindo os vértices opostos O e B, teremos o vetor soma $\color{Navy}{\vec{F}}$, dos vetores $\color{Navy}{\vec{F_1}}$ e $\color{Navy}{\vec{F_2}}$. Imagine que eles representem dois deslocamentos. Se percorrermos o segmento $\color{Navy}{\overline{OA}}$, depois $\color{Navy}{\overline{AB}}$, chegaremos à extremidade do vetor soma. Igualmente se percorrermos o segmento $\color{Navy}{\overline{OC}}$ e depois $\color{Navy}{\overline{CB}}$, iremos chegar ao mesmo ponto B, extremidade do vetor soma $\color{Navy}{\vec{F}}$  ou, $\color{Navy}{\vec{OB}}$. Vejamos como fica nosso desenho agora.

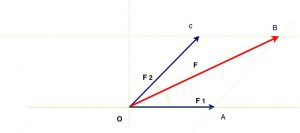
Temos agora a solução gráfica do problema. Falta aplicar os conhecimentos de geometria e trigonometria para determinar o valor numérico do vetor soma $\color{Navy}{\vec{F}}$. Note que os segmentos $\color{Navy}{\overline{OC}}$ e $\color{Navy}{\overline{AB}}$ são congruentes, assim como $\color{Navy}{\overline{OA}}$ e $\color{Navy}{\overline{BC}}$, por se tratar de lados opostos do paralelogramo.

Vamos traçar, a partir de B, um segmento perpendicular à reta que contém o vetor $\color{avy}{\vec{F_1}}$, no ponto $D$. Serão formados os triângulos retângulos $\color{Navy}{\nabla\widehat{ODBO}}$ e  $\color{Navy}{\nabla\widehat{ADBA}}$. Os ângulos $\color{Navy}{\lt\widehat{COA}}$ e $\color{Navy}{\lt\widehat{BAD}}$ são congruentes, pois são colaterais internos.

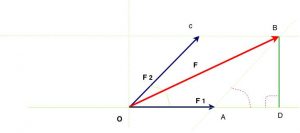
Aplicamos o teorema de pitágoras ao $\color{Brown}{\nabla\widehat{ODBO}}$. Temos a hipotenusa $\color{Navy}{\bar{F}}$, o cateto $\color{Navy}{\overline{OD}}$ formado pela soma de $\color{Navy}{\vec{F_1}}$ com o segmento $\color{Navy}{\overline{AD}}$ (x)  e o cateto $\color{Navy}{\overline{OC’}}$ $(y)$, formando dois triângulos retângulos a saber:

• $\color{Navy}{\nabla\widehat{ODBO}}$
• $\color{Navy}{\nabla\widehat{ADBA}}$
• $\color{Navy}{F^2 = \overline{BD}^2 + {\left[\overline{F_1}+ \overline{AD}\right]}^2}$
• $\color{Navy}{F^2 = y^2 + 2\cdot\overline{ F_1}\cdot \bar{x} + \bar{x}^2}$

Obtemos uma expressão com elementos estranhos introduzidos $\color{Navy}{x, y}$ e precisamos eliminá-los. Para isso vamos aplicar agora o mesmo teorema de Pitágoras ao segundo triângulo retângulo.

• $\color{Navy}{\nabla\widehat{ADBA}}$, onde a hipotenusa é o vetor $\color{Navy}{\vec{F_2}}$, e os catetos são $\color{Navy}{x , y}$, obtendo
  • $\color{Navy}{\overline{F_2}^2 =\bar{x}^2 + \bar{y}^2 }$

A soma $\color{Brown}{x^2 + y^2}$ poderá ser substituída por $\color{Navy}{\overline{F_2}^2}$.

• $\color{Navy}{\bar{F}^2 =\bar{y}^2 + \bar {x}^2 +2\cdot\overline{ F_1}\cdot\bar{x}}$
• $\color{Navy}{\bar{F}^2 = \overline{F_2}^2 + 2\cdot\overline{F_1}\cdot {x}}$

Observando a expressão ainda resta um $\color{navy}{x}$ que precisamos remover. Para isso recorremos à trigonometria. Ali encontramos que o “cateto adjacente a um ângulo, dividido pela hipotenusa, nos fornece o cosseno desse ângulo. Assim temos:

• $\color{Navy}{cos \alpha = \frac{\bar{x}}{\overline{F_2}}}$
• $\color{Navy}{cos \alpha\cdot \overline{F_2} = \bar{x}}$

Poderemos agora substituir $\color{Navy}{x}$ na expressão e o módulo do vetor resultante expresso em função de $\color{Navy}{\vec{F_1}}$, $\color{Navy}{\vec{F_2}}$ e do cosseno do ângulo entre os vetores ficará assim:

• $\color{Brown}{\bar{F_{R}^2}= \overline{F_{1}}^2 + \overline{F_{2}}^2 + 2\cdot \overline{F_{1}}\cdot\overline{F_{2}}\cdot {cos\alpha}}$.

Agora vamos determinar a direção do vetor $\color{Blue}{\vec{F}}$. Observando o ângulo $\lt\widehat{BOD}$, vemos que ele tem como cateto oposto o segmento $\color{Navy}{\overline{BD} =\bar{y}}$ e $\color{Navy}{\overline{OD} = \overline{F_1} + \overline{AD}}$ é o cateto adjacente. Da trigonometria sabemos que o “cateto oposto dividido pelo adjacente, nos fornece a tangente do ângulo. Vamos denominar o ângulo $\color{Blue}{\lt\widehat{ BOD}}$ pela letra grega $\color{Blue}{\beta}$ e teremos:

• $\color{Blue}{tg \beta = \frac {y}{{F_{1}} + x}}$

Substituindo $\color{Blue}{x}$ na expressão por $\color{Blue}{{cos\alpha}\cdot {F_2}}$, temos:

• $\color{Blue}{tg\beta = \frac {\bar{y}}{\overline{F_{1}} + \overline{F_{2}}\cdot {cos \alpha}}}$

Resta o $\color{Blue}{y}$  no numerador. Observemos no $\color{Blue}{\nabla\widehat{ ADBA}}$, o lado $\color{Blue}{\overline{BD} = \bar{y}}$, é cateto oposto ao ângulo e $\color{Blue}{\vec{F_2}}$ é a hipotenusa. Da trigonometria vem “cateto oposto dividido pela hipotenusa, é igual ao seno do ângulo”. Então:

• $\color{Blue}{{sen\alpha } = \frac {\bar{y}}{\overline{F_2}}}$

Isolando $\color{Blue}{\bar{y}}$, temos:

• $\color{Blue}{\bar{y} = {sen\alpha}\cdot \overline{F_2}}$

Substituindo na expressão da tangente de $\color{Navy}{\beta}$, temos:

• $\color{Blue}{tg\beta}  = \frac {{\overline{F_2}}\cdot{sen\alpha}}{{F_1} + {F_2}\cdot {cos\alpha}}$

Se nossas deduções estiverem corretas, essas fórmulas deverão ser aplicáveis para a adição de qualquer par de vetores, com qualquer ângulo entre eles. Vamos conferir.

• Se $\color{Blue}{\alpha = 0^{0}}$, iremos encontrar na trigonometria que o $\color{Blue}{cos\alpha = 1}$

Substituindo na fórmula do módulo do vetor resultante, temos:

• $\color{Blue}{\bar{F_{R}}^2 = \bar{F_{1}}^2  + \bar{F_{2}}^2 + 2\cdot\bar{F_{1}}\cdot\bar{F_{2}}\cdot cos\alpha}$
• $\color{Blue}{\bar{F}^2 = \bar{F_{1}}^2  + \bar{F_{2}}^2 + 2\cdot\bar{F_{1}}\cdot\bar{F_{2}}\cdot {1}}$

Resultou no segundo membro um trinômio quadrado perfeito, que podemos fatorar no quadrado da soma de $\bar{F_1}$ e $\bar{F_2}$, ficando pois:

• $\color{Blue}{\bar{F_{R}}^2 = \{\bar{ F_{1}} + \bar{F_{2}}\}^2}$

Os dois membros da equação são quadrados perfeitos e podemos extrair a raiz quadrada, ficando:

. $\sqrt{\bar{F_{R}}}^2 = \sqrt{\{\bar{F_{1}} + \bar{F_{2}}\}^2}$

• $\color{Blue}{\bar{F_{R}} = \bar{F_{1}} + \bar{F_{2}}}$

Isso confere com o que vimos quando falamos da adição de vetores de mesma direção e sentido. O Vetor soma é a soma dos módulos dos vetores. A direção é a mesma dos vetores somados.

•  Se o angulo $\color{Blue}{\alpha = 90^{0}}$$\color{navy}{sen{90º} = 1}$ e o $\color{Blue}{cos {90º} = 0}$, substituindo na mesma fórmula, temos.
• $\color{Blue}{\bar{F}^2 = \bar{F_1}^2 + \bar{F_2}^2 + 2\cdot\bar{F_1}\cdot\bar{F_2}\cdot cos{90º}}$
• $\color{Blue}{\bar{F}^2 = \bar{F_1}^2 + \bar{F_2}^2 + 2\cdot\bar{F_1}\cdot\bar{F_2}\cdot{0}}$

Um termo multiplicado por 0(zero), é nulo e resta.

• $\color{Blue}{\bar{F_{R}}^2 = \bar{F_{1}}^2 + \bar{F_{2}}^2}$

Expressão que é o Teorema de Pitágoras aplicado para esse caso.

•  Se o angulo $\color{Navy}{\alpha = 180º}$, temos $\color{Blue}{sen180^{0} = 0}$ e $\color{Blue}{cos 180^{0} = -1}$. Vamos substituir na equação.
• $\color{Blue}{\bar{F_{R}}^2 = \bar{F_{1}}^2 +  \bar{F_{2}}^2 + 2\cdot\bar{F_{1}}\cdot \bar{F_{2}}\cdot cos 180^{0}}$
• $\color{Blue}{\bar{F_{R}}^2 = \bar{F_{1}}^2 +  \bar{F_{2}}^2 + 2\cdot\bar{F_{1}}\cdot \bar{F_{2}}\cdot {-1 }}$

• $\color{Blue}{\bar{F_{R}}^2 = \bar{F_{1}}^2 + \bar{F_{2}}^2 – 2\cdot \bar {F_{1}}\cdot\bar{F_{2}}}$

Novamente resultou um trinômio quadrado perfeito, que pode ser fatorado no quadrado da diferença. Assim:

• $\color{Blue}{\bar{F_{R}}^2 = (\bar{ F_{1}} – \bar{F_{2}})^2}$

Extraindo a raiz quadrada de ambos os membros, resulta:

• $\color{Blue}{\bar{F_{R}} = \bar{F_{1}} – \bar{F_{2}}}$

O que nos dá a diferença entre os vetores de mesma direção e sentidos opostos. Dessa forma fica demonstrado que a expressão obtida acima é válida para qualquer ângulo entre dois vetores. Com certeza nos casos particulares fica mais fácil aplicar a forma simplificada. Mas se usarmos a fórmula geral obteremos o mesmo resultado.

• Para exercitar um pouco, vamos calcular a soma dos vetores:
  • $\color{Brown}{\vec{V_{a}} = 5 un }$ e $\color{Brown}{\vec{V_{b}} = 10 un}$. Considere o ângulo entre eles $30^{0}, 45^{0} e 60^{0}$.
  • $\color{Brown}{\vec{F_{1}} = 6 N}$. $\color{Brown}{\vec{F_{2}} = 8 N}$. Ângulos de $60^{0}, 120^{0}$.
  • $\color{Brown}{\vec{M_{1}} = 12 un}$ e $\color{Brown}{\vec{M_{2}} = 15 un}$, para ângulos de $30^{0} e 150^{0}$.
  • $\color{Brown}{\vec{N_{1}} = 12 un}$ e $\color{Brown}{\vec{N_{2}} = 16 un}$, para ângulo de$0^{0}, 90^{0} e 180^{0}$.

Em caso de dúvida, me consulte por um dos canais que estão listados abaixo.

Curitiba, 18/março/2015( Atualzado em 01 de agosto de 2016)

Décio Adams

[email protected]

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@DcioAdams

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732

Tags: #adição de vetores, #estática, #física, #mecânica, #paralelogramo, #Teorema de Pitágoras, vetor resultante