Exercícios de hidráulica.
Ajudando alguém e compartilhando.
O meu sobrinho Evandro Luis Adams, residente em Brasnorte, formado em Agronomia do Trópico Úmido na escola internacional localizada na Costa Rica, pediu minha ajuda para um colega, que está com dificuldades em Hidráulica. Fizemos contato e ele me passou uma lista de exercícios a ser resolvida. Matéria para prova.
Pela exiguidade do tempo disponível, resolvi alguns exercícios para ele e vou compartilhar aqui. Assim ele terá acesso e outros também poderão aproveitar. Em outro momento posso desenvolver o conteúdo teórico com mais detalhes, coisa que no momento é impraticável. Vamos ao primeiro exercício, identificado pela SIGLA:
1. ED 01
Determinar a pressão manométrica em A, devido à deflexão do mercúrio do manômetro em U da figura abaixo. O líquido escoante é água $\color{navy}{\gamma_{H_{2}O} = 1000,0 kgf.m^{-3}}$ e o líquido manométrico é $\color{navy}{\gamma_{Hg} = 13600,0 kgf\cdot m^{-3}}$.
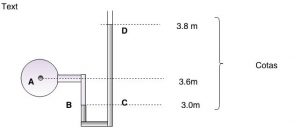
A pressão manométrica, não leva em consideração a pressão atmosférica e é também chamada de pressão relativa, podendo apresentar valores positivos e negativos. Nesse caso a pressão atmosférica é indicada pelo valor 0(zero).
A água que flui no conduto A, apresenta uma pressão, medida pelo manômetro. Para iniciar a resolução escolhemos dois pontos situados no mesmo nível de um mesmo líquido, submetidos à mesma pressão. No caso vamos encontrar isso nos pontos B e C. Ambos estão no mesmo nível do líquido manométrico “mercúrio”.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{B} = P_{C}}\qquad (1)}\] \[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{B} =P_{A} + \gamma_{H2O}\cdot h_{AB}}\qquad (2)}\] \[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{C}= P_{atm} + \gamma_{Hg}\cdot h_{CD}}\qquad (3)}\]
As alturas entre os pontos AB e CD são obtidas através das cotas indicadas na figura.
\[h_{AB} = {3,6 – 3,0} = 0,6 m\]
\[h_{CD}= {3,8 – 3,0}= 0,8 m\]
Substituindo (2) e (3) em (1) e colocando no lugar da pressão atmosférica o seu valor 0(zero), teremos.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{A} + \gamma_{H_{2}O}\cdot h_{AB}= P_{atm} + \gamma_{Hg}\cdot h_{CD}}\qquad (4)}\] \[P_{A} + 1000,0\cdot {0,6} = 0 + 13600,0\cdot {0,8}\] \[P_{A} + 600,0 = 10880,0\] \[P_{A}=10880,0 – 600,0 = 10280,0 kgf.m^{-2}\]
Temos aí a resposta. A água em escoamento no tubo A, está a uma pressão de $\color{blue}{10280,0 kgf/m²}$ o que também pode ser expresso por$\color{blue}{ 1,028 kgf/cm²}$.
2. ED 02
Os recipientes A e B da Figura, contém água sob pressão $\color{navy}{p_{A}= 3,0 kgf/cm²}$ e $\color{navy}{p_{B} =1,5 kgf/cm²}$, respectivamente. Qual será a deflexão (desnível) do mercúrio (h) no manômetro diferencial? Líquido escoante é água e o líquido manométrico é mercúrio. Seus pesos específicos valem respectivamente:
\[\color{navy}{\gamma_{H_{2}O}= 1000,0kgf/m³} \] \[\color{navy}{\gamma_{Hg}= 13600,0 kgf/m³}\]
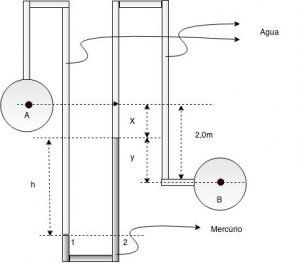
Vamos partir dos pontos (1) e (2), situados na separação entre água e mercúrio e no interior do mercúrio. Estando no mesmo nível no interior de um líquido, estão submetidos à mesma pressão.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{1} = P_{2}}\qquad (5)}\]
As pressões nos dois pontos são dadas pelas expressões.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{1}= P_{A} + \gamma_{H_{2}O}\cdot {h + x}}\qquad(6)}\] \[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{2}= P_{B} + \gamma_{H_{2}O}\cdot x + \gamma_{Hg}\cdot h – \gamma_{H_{2}O}\cdot 2,0}\qquad(7)}\]
Nos pontos A e B, a pressão da água é \[P_{A} = 3,0 kgf\cdot{cm^2} = 3,0\cdot{10^4} kgf/m²\] \[P_{B} = 1,5 kgf/cm² = 1,5\cdot {10^4} kgf/m²\]
Substituindo as expressões (6) e (7) em (5), temos:
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{A} + \gamma_{H_{2}O}\cdot {(h + x)}=P_{B} +\gamma_{H_{2}O}\cdot x + \gamma_{Hg}\cdot h – \gamma_{H_{2}O}\cdot {2,0}}\qquad(8)}\]
\[3,0\cdot {10}^4 + 1,0\cdot{10}^3\cdot {(h+x)} = 1,5\cdot{10}^4 + 1,0\cdot{10}^3\cdot x + 13,6\cdot {10}^3\cdot h – 1,0\cdot {10}^3\cdot {2,0}\] \[3,0\cdot{10}^4 + {10^3}\cdot h + {10^3}\cdot x = 1,5\cdot{10}^4 + {10}^3\cdot x + 13,6\cdot {10}^3\cdot h – {2,0}\cdot{10}^3\]
Temos termos simétricos no primeiro e segundo membro que podem ser cancelados ${10^3\cdot x} $ e isolando a única variável que resta (h) no primeiro membro da equação.
\[{10}^3\cdot h – 13,6\cdot{10}^3\cdot h= 1,5\cdot{10}^4 – 3,0\cdot{10}^4 – 2,0\cdot{10}^3\] \[-12,6\cdot{10}^3\cdot h = -1,7\cdot{10}^4\] \[ h = {{- 1,7\cdot{10}^4}\over {- 12,6\cdot {10^3}}}\] \[h = {17\over{12,6}}\] \[ h = 1,3492 m\]
A deflexão do mercúrio no manômetro diferencial (desnível) é de $\color{blue}{1,3492 m}$.
3. ED 03
Duas canalizações estão dando escoamento à água $\color{navy}{\gamma_{H_{2}O}= 10^3 kgf\cdot m^{-3}} $, sob pressão (condutos forçados). Deseja-se determinar a diferença de pressão entre duas seções A e B das duas canalizaões, empregando-se o manômentro diferencial de mercúrio. Sabe-se que o centro das duas seções apresentam uma diferença de nível de $\color{navy}{8,7 m}$ e que a deflexão do mercúrio é de 0,88 m. Sabe-se que o peso específico do mercúrio é $\color{navy}{\gamma_{Hg} = 13,6\cdot{10}^3kgf\cdot m^{-3}}$
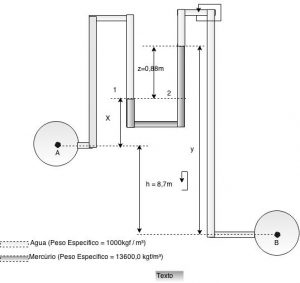
O enunciado pede a diferença de pressão entre os condutos A e B, sendo conhecida a pressão indicada pelo manômetro diferencial (0,880 mmHg). Novamente vamos partir da igualdade entre as pressão nos pontos (1) e (2), situados no mesmo líquido (mercúrio), sujeitos à mesma pressão.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{1}=P_{2}}\qquad(9)}\]
As pressões nesses dois pontos são dadas por;
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{1}= P_{A} – \gamma_{H_{2}O}\cdot x}\qquad(10)}\] \[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{2} =P_{B} +\gamma_{Hg}\cdot z – \gamma_{H_{2}O}\cdot y}\qquad(11)}\]
Substituindo (10) e (11) em (9) teremos.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{A} – \gamma_{H_{2}O}\cdot x= P_{B} + \gamma_{Hg}\cdot z – \gamma_{H_{2}O}\cdot y}\qquad(12)}\]
Colocando as pressões no primeiro membro e o restante dos termos no segundo, teremos.
\[P_{A} – P_{B} = 13,6\cdot{10}^3\cdot{0,88} – {10}^3\cdot y +{10}^3\cdot x\]
\[P_{A} – P_{B} = 11,968\cdot{10}^3 + (x – y )\cdot {10^3}\]
OBS.: Colocamos em evidência a potência de 10 e surgiu entre parênteses a diferença (x – y). Olhando na figura vemos que essa diferença pode ser obtida por:
\[{ x + z + 8,7} = y\] \[x – y= -0,88 – 8,7= – 9,58 m\]
Substituindo este valor na expressão anterior, teremos.
\[P_{A} – P_{B} = 11,968\cdot{10^3} + {- 9,58}\cdot {10^3}\]
\[P_{A} – P_{B} = {(11,968 – 9,580)}\cdot{10}^3 = 2,388\cdot{10}^3kgf\cdot m^{-2}
\]
A diferença de pressão entre os condutos A e B é de $\color{navy}{2,388.10³ kgf/m²}$.
4. ED 04
O tubo A contém óleo ($\color{blue}{d = 0,8}$) e o tubo B , água ($\color{blue}{peso}$ $\color{blue}{ espec \acute {i} fico = 1000,0 kgf/m³}$). Calcular as pressões em $\color{navy}{ A}$ e $\color{navy}{B}$ para as indicações do manômetro.
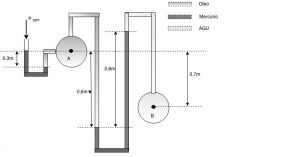
A pressão no Tubo A, é calculado pelo desnível do mercúrio no manômetro em forma de U, existente ao lado esquerdo. Vamos determinar a pressão manométrica ou relativa. Note que o nível do mercúrio fica na mesma altura do ponto A. Daí podemos escrever que:
\[\color{navy}{P_{A} + \gamma_{óleo}\cdot {0,3}= \gamma_{Hg}\cdot {0,3}}\]
Substituindo os valores dos pesos específicos e isolando a pressão em A no primeiro membro.
\[P_{A}= 13,6\cdot{10}^3 – {0,8}\cdot{10}^3\cdot {0,3}\]
\[ P_{A}= {(13,6 – 0,24)}\cdot {10}^3\]
\[P_{A} = 13,36\cdot {10}^3kgf\cdot m^{-2}\]
A pressão do óleo está um pouco abaixo da pressão atmosférica e vale 13360,0 kgf/m².
Agora podemos partir de dois pontos situados (1) e (2), no mesmo nível, no interior do mercúrio.
\[\color{navy}{P_{1} = P_{A} + \gamma_{óleo}\cdot{0,6}}\]
\[P_{2} =P_{B} + \gamma_{Hg}\cdot{0,8} – \gamma_{H_{2}O}\cdot{(0,7 +0,8 – 0,6)}\]
Igualando as duas expressões teremos:
\[P_{A} + \gamma_{óleo}\cdot{0,6} = P_{B} + \gamma_{Hg}\cdot{0,8} – \gamma_{H_{2}O}\cdot{0,9}\]
Substituindo os valores dos pesos específicos e da pressão em A por seus valores, teremos:
\[13360 + {0,8}\cdot{10}^3\cdot{0,6} = P_{B} + {13,6}\cdot{10}^3\cdot{0,8} – {0,9}\cdot{10}^3\]
\[13360 + 480 = P_{B} + 10880 – 900\]
\[13840 = P_{B} + 9980\] \[13840 – 9980= P_{B}\] \[P_{B} = 3860 kgf/m²\]
Temos pois as duas pressões pedidas no enunciado. No ponto A a pressão é $\color{navy}{13360 kgf/m²}$, e no ponto B $\color{navy}{ 3860kgf/m²}$
5. ED 05
Os reservatórios fechados R e S da figura, contém respectivamente, água ($\color{navy}{peso}$ $\color{navy}{ espec \acute{i} fico = 1000,0 kgf/m³}$) e um líquido de peso específico $\color{navy}{\gamma_S }$. Sabe-se que a pressão em R é igual a $\color{navy}{1,1 kgf/cm²}$ e no ponto S a pressão é igual a $\color{navy}{ 0,8 kgf/cm²}$. Calcular o valor do peso específico do líquido $\color{navvy}{S}$.
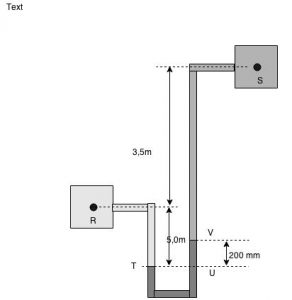
A pressão nos pontos T e U é igual. Eles encontram-se no interior do líquido manométrico (vou considerar como sendo mercúrio uma vez que não foi fornecido no enunciado).
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{T}=P_{U}}\qquad(13)}\]
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{T}= P_{R} + \gamma_{H_{2}O}\cdot {5,0}}\qquad(14)}\]
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{U}= P_{S} +\gamma_{Hg}\cdot{0,20}+\gamma_{S}\cdot {8,50 – 0,20}}\qquad(15)}\]
Substituindo as expressões (14) E (15) na na igualdade (13) teremos:
\[P_{R} + \gamma_{H_{2}O}\cdot{5,0}= P_{S} + \gamma_{Hg}\cdot{0,20} + \gamma_{S}\cdot{8,50 – 0,20}\]
\[11\cdot{10}^3 + 5,0\cdot{10}^3=3 = {8,0}\cdot{10}^3+ {13,6}\cdot{10}^3\cdot{0,20} +\gamma_{S}\cdot{8,3}\]
\[16,\cdot{10^3}= {8,0}\cdot{10}^3 + {2,72}\cdot{10}^3 + \gamma_{S}\cdot{8,3}\]
\[\gamma_{S}\cdot{8,3}= {16,0}\cdot{10}^3 – {10,72}\cdot{10}^3\]
\[\gamma_{S} = {{5,28\cdot{10}^3}\over{8,3}} \]
\[\gamma_{S} = {0,636}\cdot{10^3} = {6,36}\cdot{10}^2 kgf\cdot m^{-3}\]
\[\gamma_{S} = 636 kgf\cdot m^{-3}\]
O peso específico do líquido S é $\color{blue}{ 636 kgf/m³}$.
6. ED 06
Uma comporta circular vertical de 0,90 m de diâmetro, trabalha sob pressão de melado ($\color{navy}{densidade = 1,50}$ ), cuja superfície livre está $\color{navy}{ 2,40 m}$, acima do topo da mesma. Calcular o empuxo (E) e a posição do centro de pressão.
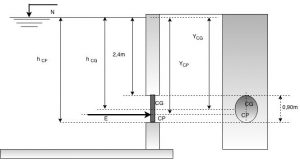
A força de empuxo é igual ao produto da profundidade do CG da comporta, pelo peso específico do líquido, pela área da comporta.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{F_{E} = h_{CG}\cdot\Gamma\cdot A}\qquad(16)}\]
\[ F_{E} = {(2,4 + 0,45)}\cdot{1,5}\cdot{10}^3\cdot\pi\cdot{0,45}^2\]
\[F_{E} = 2,71964\cdot{10}^3 kgf\]
A força de empuxo é de $\color{blue}{ 2,719,64 kgf}$.
Para determinarmos a profundidade do ponto de aplicação da força de empuxo, isto é o centro de pressão, precisamos determinar o momento de inércia da comporta (círculo). Podemos usar a fórmula a seguir. O diâmetro da comporta é $\color{navy}{ 0,90 m}$ e a profundidade de seu CG é igual ao seu raio($\color{navy}{d/2}$) somado à distância entre o topo e s superfície ($\color{navy}{2,40m}$).
\[ I_{0} ={{ \pi\cdot d^4}\over{64}}\]
\[ I_{0} ={{\pi\cdot{(0,9)^4}}\over{64}}\]
\[\color{blue}{ I_{0} = 0,0322 kg.m^2}\]
No Sistema técnico teremos:
\[\color{blue}{I_{0}= {{0,0322}\over {9,8}} = 0,003286 = 3,286\cdot{10}^{-3} utm\cdot m^2}\]
Para determinar a posição do centro de pressão usamos a expressão.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{Y_{CP} = Y_{CG} + {{I_{O}}\over{A\cdot{Y_{CG}}}}\qquad(17)}}\]
\[ Y_{CP} = {2,4 + 0,45} +{{0,0322}\over{{\pi\cdot{(0,9)^2}}\over {4}}\cdot {2,85}}\]
\[Y_{CP} = 2,85 + {{0,0322}\over{1,8131}}\]
\[Y_{CP} ={ 2,85 + 0,018}\]
\[\bbox[silver,5px,border:2px solid olive]{\color{blue}{Y_{CP} = 2,868 m}}\]
O centro de pressão, fica situado a profundidade de $\color{blue}{ 2,868 m}$, sobre a vertical que passa pelo centro de gravidade da comporta, coincidente com o centro geométrico.
7. ED 07
Qual a pressão, em $\color{navy}{ kgf/m²}$ e em $\color{navy}{kgf/cm²}$, no fundo de um reservatório com três metros de profundidade que contém água até a borda? E se o reservatório contivesse água do mar? Obs.:A densidade da água do mar é $\color{navy}{ 1,024}$. Água doce tem peso específico $\color{navy}{1000,0 kgf/m³}$.
A pressão manométrica será dada por:
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{ P_{água} = \gamma_{H_{2}O}\cdot{Y}}}\]
\[P_{água} = {10}^3\cdot{3,0}\]
\[\color{blue}{P_{água} = 3000,0 kgf/m²}\]
Para obter o resultado em $\color{navy}{kgf/cm²}$, basta dividir por $\color{navy}{{10}^4}$
\[{3000,0 kgf/m²}= {{3000}\over{10^4}} kgf/cm²\]
\[\color{blue}{ P_{água}= 0,3 kgf/cm²}\]
Se quisermos a pressão total, incluindo a ação da atmosfera sobre a superfície, teremos que adicionar o valor $\color{navy}{{10}^5 Pa} $ a esses valores, evidentemente transformado para as unidades convenientes.
Se o recipiente contivesse água do mar (salgada), cuja densidade é $\color{navy}{ 1,024}$, teríamos:
\[\color{navy}{\gamma_{mar} = 1,024\cdot{10}^3 kgf/m³}\]
Substituindo na expressão da pressão, teremos:
\[P_{mar} = \gamma_{mar}\cdot{3,0}= 1,024\cdot{10^3}\cdot{3,0}\]
\[\color{blue}{P_{mar}= 3,072\cdot{10^3} = 3072,0 kgf/m²}\]
ou \[\color{blue}{ P_{mar} = {{3072,0}\over{10}^4} = 0,3072 kgf/cm²}\]
Se quisermos a pressão absoluta, teremos que somar o valor da pressão atmosférica local aos valores obtidos para a manométrica.
8. ED 08
A pessão atmosférica de uma determinada localidade (pressão barométrica) é de $\color{navy}{740 mm_{Hg}}$. Expressar a pressão manométrica de $\color{navy}{0,25 kgf/cm²}$, de forma relativa e absoluta, nas unidades $\color{navy}{kgf/m²}$,$\color{navy}{ kPa}$ (quilo Pascal),$\color{navy}{ bar}$,$\color{navy}{ metros}$ $\color{navy}{ de}$ $\color{navy}{ coluna}$ $\color{navy}{de}$ $\color{navy}{ água}$ e $\color{navy}{ mm_{Hg}}$. Obs. $\color{navy}{1 atm física = 10330,0 kgf/m²= 101,3 kPa = 1,013 bar = 10,33 m_{H_{2}O} = 760 mm_{Hg}}$.
Sendo a pressão fornecida a manométrica ou relativa, bastará converter seu valor para as unidades pedidas. Depois, adicionaremos a cada um o valor correspondente da pressão atmosférica para obter o valor absoluto.
Sabemos da matemática que $\color{teal}{{ 1cm²} = {10}^{-4}m²} $
Logo vamos dividir a unidade por esse valor e teremos o mesmo espresso em $\color{navy}{kgf/m²}$
\[{0,25 kgf/cm²}= {{0,25}\over{10}^{-4}} = \color{blue}{2500 kgf/m²}\]
\[{2500 kgf/m²} = {{{2500}\cdot{9,8}}\over{10^3}}=\color{blue}{ 24,5 kPa}\]
\[{24,5 kPa} = {{24,5}\over{100}} =\color{blue}{ 0,245 bar}\]
\[{2500 kgf/m²} = {{2500}\over{10}^3} =\color{blue}{ 2,5 m_{H_{2}O}} \]
\[{{10330}\over{2500}} = {{760}\over x}\]
\[ x={{760\cdot{2500}}\over{103030}} =\color{blue}{ 183,93mm_{Hg}}\]
Temos pois a pressão relativa:
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{0,25 kgf/cm² = 2500 kgf/m² = 24,5 kPa = 0,245 bar = 2,5 m_{H_{2}O} = 183,93 mm_{Hg}}}\]
A pressão absoluta será obtida adicionando a esses valores os valores correspondentes da pressão atmosférica.
\[{2500 + 10330 }=\color{blue}{ 12830 kgf/m²}\]
\[{24,5 + 101,3}kPa =\color{blue}{ 125,8 kPa}\]
\[{0,245 + 1,013} bar =\color{blue}{ 1,258 bar}\]
\[{2,5 + 10,330} m_{H_{2}O} =\color{blue}{ 12,830 m_{H_{2}O}}\]
\[{183,93 + 760} mm_{Hg} =\color{blue}{ 943,93 mm_{Hg}}\]
Assim:\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{ 12830kgf/m² = 125,8 kPa = 1,258 bar = 12,830 mH20 = 943,93 mmHg}} \]
9. ED 09
Qual o valor da pressão registrada nas formas absoluta e relativa, a 10m de profundidade em água do mar?($\color{navy}{d = 1,024}$). Obs.: considerar que a leitura de um barômetro de mercúrio na superfície foi iguala$\color{navy}{758 mm_{Hg}}$.
\[P_{rel} = 1,024\cdot {10}^3\cdot {10} = 1,024\cdot{10}^4 kgf/m²\]
A pressão absoluta será \[p_{abs} = P_{rel} + P_{atm} = {1,024}\cdot{10}^4 +{13600\cdot{0,758}}\]
\[ P_{abs} = {10240,0 + 10380,0 } = 20620 kgf/m²\]
A pressão absoluta é portanto igual a $\color{blue}{20620,0 kgf/m²}$.
A pressão relativa é $\color{blue}{ 10240,0 kgf/m²}$.
10. ED 10
Se a pressão num manômetro, instalado na base de um tanque de óleo, cuja densidade relativa é $\color{navy}{0,8}$, é igual a $\color{navy}{ 4,2 kgf/cm²}$, qual o valor da altura da coluna de óleo no tanque? Se a mesma pressão fosse registrada no manômetro, com líquidos diferentes no tanque, qual a altura da coluna formada em metros de coluna de água e em metros de coluna de mercúrio?
A pressão determinada é a relativa ou manométrica. Temos pois:
\[P_{rel}= {0,8}\cdot{10}^3\cdot h\]
\[{4,2\cdot {10}^3} = 800\cdot h\]
\[{4200\over {800}} = h\] \[\color{blue}{ h = 5,025 m}\]
Para água teríamos:
\[{4200} = 1000\cdot h_{H_{2}O}\] \[\color{blue}{h_{H_{2}0} = {4200\over{1000}} = 4,2 m}\]
Para mercúrio:
\[ 4200 =13600\cdot {h_{Hg}}\] \[ h_{Hg} ={4200\over{13600}}\] \[\color{blue}{h_{Hg}= 0,31 m}\]
11. ED 11
Calcular a pressão existente no ponto D, localizado no centro de uma tubuliação, a partir da leitura de um manômetro de mercúrio em forma de U. Forneça o resultado nas unidades de pressão:$\color{navy}{ kgf/m²}$, $\color{navy}{ metros}$ $\color{navy}{ de}$ $\color{navy}{ coluna}$ $\color{navy}{ de}$ $\color{navy}{ água}$ e em $\color{navy}{centímetros}$ $\color{navy}{de}$ $\color{navy}{ coluna}$ $\color{navy}{de}$ $\color{navy}{ Hg}$. São dados: $\color{navy}{h = 0,76 m}$; $\color{navy}{z = 0,35 m}$; $\color{navy}{ peso}$ $\color{navy}{ específico}$ $\color{navy}{ da}$ $\color{navy}{ água = 1000,0 kgf/m³}$ e $\color{navy}{peso}$ $\color{navy}{específico}$ $\color{navy}{do}$ $\color{navy}{mercúrio = 13600,0 kgf/m³}$.
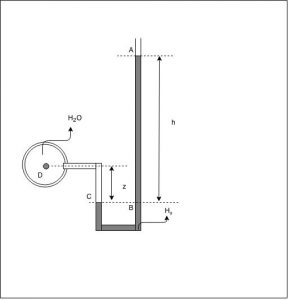
Partimos da igualdade de pressões nos pontos B e C, no interior do manômetro.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{C}=P_{B}}\qquad(18)}\]
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{C}= P_{D} + \gamma_{H_{2}O}\cdot Z}\qquad(19)}\]
\[\bbox[silver,5px,borcer:2px solid olive]{\color{navy}{P_{B} = P_{atm} + \gamma_{Hg}\cdot h}\qquad(20)}\]
A pressão em D é manométrica ou relativa, portanto considera a pressão atmosférica como referência e lhe atribuímos o valor 0(zero). Substituindo (19) e (20) em (18), teremos:
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{D} + \gamma_{H_{2}O}\cdot Z = P_{atm} + \gamma_{Hg}\cdot h}\qquad(21)}\]
\[ P_{D} + {10}^3\cdot{0,35}= 0+ 13600\cdot {0,76}\]
\[ P_{D} = 10336 – 350\] \[\color{blue}{P_{D} = 9986 kgf/m²}\]
Temos a pressão no ponto D igual a $\color{blue}{9986,0 kgf/m²}$.
Sabemos que $\color{navy}{1 atm = 10330 kgf/m²= 760mm_{Hg}}$. Podemos então estabelecer a proporção.
\[{{760}\over {X}} = {{10330}\over {9986}}\]
\[{X} = {{760\cdot9986}\over10330}\]
\[\color{blue}{X= 734,69 mm_{Hg}}\]
Também podemos usar $\color{navy}{760mmHg = 10,33 m_{H_{2}O}}$.
\[{760\over {734,69}}= {10,33\over Y}\]
\[ Y = {{10,33\cdot{734,69}}\over{760}}\]
\[\color{blue}{Y = 9,98 m_{H_{2}O}}\]
12. ED 12
Considere a comporta da figura. Se a altura da água for de $\color{navy}{ 5,0 m}$, a altura da comporta é $\color{navy}{ 3,0 m}$ e a largura é de $\color{navy}{ 4,0 m}$, determine o centro de pressão e a força de empuxo.
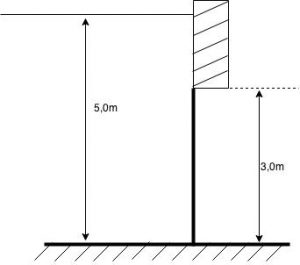
A área da comporta é:
\[\color{maroon}{A=3,0\cdot{4,0}= 12,0 m^2}\]
A profundidade do centro de gravidade é dada pela profundidade do reservatório subtraido da metade da altura da comporta.
\[\color{maroon}{h_{CG}= 5,0 – {3,0\over2} = 5,0 – 1,5 = 3,5 m}\]
\[\color{maroon}{I_{O}= {b\cdot{h}^3\over {12}}}\]
\[ I_{O}= {{4\cdot{3}^3}\over{12}}\]
\[\color{blue}{I_{O}= 9 m^2}\]
A posição do centro de pressão dessa comporta é dada apor:
\[h_{CP} = h_{CG} +{{I_{O}}\over{A\cdot {h_{CG}}}}\]
\[h_{CP} = 3,5 + {9\over{12\cdot{3,5}}}={3,50 + 0,214}\]
\[\color{blue}{ h_{CP} = 3,714 m}\]
A força de Empuxo sobre a comporta é dada por:
\[ F_{E} = h_{CG}\cdot{10}^3\cdot{12}\]
\[ F_{E} = 3,5\cdot{10}^3\cdot{12}= {42\cdot{10^3}}\]
\[\color{blue}{ F_{E} = 42000,0 kgf}\]
13. ED 13
Duas canalizações estão em escoamento Fluido A( $\color{navy}{γ = 1750,0 kgf/m³}$) e Fluido B. Os líquidos manométricos $\color{navy}{ 01}$ e $\color{navy}{ 02}$ apresentam respectivamente $\color{navy}{ 13600,0 kgf/m³}$ e $\color{color}{ 2750,0 kgf/m³}$, conforme mostrado na figura abaixo. Supondo que a diferença de pressão entre os condutos A e B seja igual a $\color{navy}{ 0,0258 kgf/cm²}$, determine o peso específico do fluido B? Considere $\color{navy}{X = 750,0 mm}$; $\color{navy}{ Y = 1,50 m}$ e $\color{navy}{Z = 9,80 cm}$.
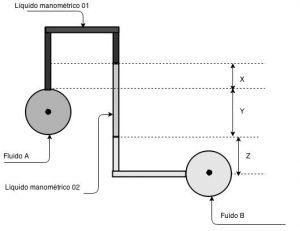
Vamos começar por dois pontos no líquido manométrico 01(mercúrio), que iremos chamar de 1
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{1}=P_{2}}\qquad(22)}\]
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{1} =P_{A} – \gamma_{01}\cdot X}\qquad(23)}\]
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{2} = P_{B} – \gamma_{02}\cdot{( X + Y)} – \gamma_{B}\cdot{Z}}\qquad(24)}\]
Substituindo (23) e (24) em (22), temos:
\[\color{maroon}{P_{A} – \gamma_{01}\cdot{X}= P_{B} – \gamma_{02}\cdot{(X + Y)} + \gamma_{B}\cdot{Z}}\]
Isolando no primeiro membro as pressões dos dois condutos A e B, temos:
\[\color{maroon}{P_{A} – P_{B} = \gamma_{01}\cdot {X} -\gamma_{02}\cdot{(X + Y)} – \gamma_{B}\cdot{Z}}\]
Vamos substituir os valores das variáveis.
\[258,0 = 13600,0\cdot{0,75} – 2750,0\cdot{(0,75 + 1,5)} – {0,98}\cdot\gamma_{B}\]
\[{258,0} = {10200,0 – 6187,5} – {0,98}\cdot\gamma_{B}\]
\[{0,98}\cdot\gamma_{B}= {4012,5 – 258,0}\]
\[\gamma_{B}= {{3754,5}\over{0,98}}\]
\[\color{blue}{\gamma_{B} = 3831,12 kgf/m³}\]
14. ED 14
Considerando a Figura apresentada no ED 13, assumindo que a pressão no conduto B corresponde a $\color{navy}{8,83 m_{H_{2}O}}$(metros de coluna d’água), quais os valores que X e Y assumiriam, se neste sistema tivéssemos somente o líquido manométrico $\color{navy}{01}$ ?
Se a pressão em B é $\color{teal}{8,83 m_{H_{2}O}}$, isso permite determinar que o seu valor em $\color{teal}{kgf/m²}$, seja igual a:
\[\color{blue}{P_{B} = 8,83\cdot{10}^3kgf/m²}\]
A diferença de pressão entre A e B :
\[ P_{A} – P_{B} = {0,0258\over{10}^{-4}}=\color{blue}{258kgf/m²}\]
Daí tiramos que: \[P_{A} = {8830 + 258} = \color{blue}{9080 kgf/m²}\]
Os pontos com mesma pressão continuam a ser os mesmos, situados no interior do líquido manométrico 01.
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{P_{A} – \gamma_{Hg}\cdot X = P_{B} – \gamma_{Hg}\cdot{(X + Y)} – \gamma_{B}\cdot{0,098}}\qquad(25)}\]
Isolando as pressões nos pontos $\color{navy}{A}$ e $\color{navy}{B}$, ficamos com:
\[\color{maroon}{P_{A} – P_{B} = \gamma_{Hg}\cdot X – \gamma_{Hg}\cdot{(X + Y)} – \gamma_{B}\cdot{0,098}}\]
\[9080 – 8830 = 13600\cdot X – 13600\cdot{(X + Y)} – 3831,12\cdot{0,098}\]
\[258 = 13600\cdot X – 13600\cdot X – 13600\cdot Y – 375,35\]
Os dois termos com a variável X, tem coeficientes simétricos, portanto se cancelam.
\[ 258 + 375,45 = 13600\cdot Y\]
\[{ 633,45\over13600}= Y\]
\[\color{blue}{ Y = 0,047 m}\]
Como agora só existe um líquido manométrico, na verdade o valor de X se cancela e portanto podemos considerá-lo nulo. O desnível ou deflexão do líquido manométrico 01(mercúrio) é igual ao valor acima: 0,047 m.
15. ED 15
Calcular a força de Empuxo exercida pela água sobre uma comporta quadrada de área igual a $\color{navy}{2,25 m²}$, em que a extremidade superior está a $\color{navy}{ 5,45 m}$ abaixo da superfície. A comporta está alinhada com o aterro da barragem, inclinada de $\color{navy}{ 30º}$ em relação à vertical. Considere o peso específico da água igual a $\color{navy}{ 1000,0 kgf/m³}$.
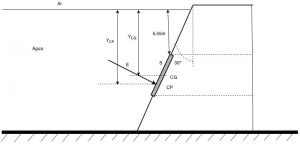
Se a área da comporta quadrada é 2,25 m², lado, pois:
\[\bbox[silver,5px,border:2px solid olive]{\color{maroon}{ S = {l}^2}}\]
\[2,25 = {l}^2\]
\[\sqrt{2,25} = \sqrt{l}^2 \] \[\color{blue}{ l = 1,5 m}\]
Como o CG está situado à metade da altura do quadrado, ele situa-se a 0,75 m, do topo da comporta, segundo a inclinação de 30º em relação à vertical. A projeção vertical é o cateto adjacente ao ângulo, e:
\[ X = {l\over 2}\cdot{{\sqrt 3}\over2}\]
\[ X = {1,5\over 2}\cdot {0,866} =\color{blue}{ 0,65 m}\]
A profundidade do CG é portanto: \[ h_{CG} = 5,45 + 0,65\]
\[\color{blue}{ h_{CG} = 6,10 m}\]
\[\bbox[silver,5px,border:2px solid olive]{\color{navy}{F_{E} = h_{CG}\cdot\gamma_{H_{2}O}\cdot {S}}}\]
\[ F_{E} = 6,10\cdot{1000,0}\cdot{2,25}\]
\[\color{blue}{F_{E} = 13725,0 kgf}\]
16. ED 16
Determine a diferença de pressão entre a tubulação de água e a tubulação de óleo. Considere o esquema mostrado abaixo.
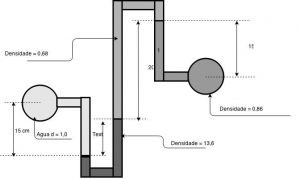
Começamos pelos dois pontos de mesmo nível e mesma pressão no interior do mercúrio($\color{navy}{d=13,6}$).
\[\bbox[silver,5px,border:2px solid olive]{\color{maroon}{ P_{1} = P_{2}}}\]
\[ P_{A}+ 1000,0\cdot{0,15} = P_{oleo} + 13600\cdot{0,10} + 680\cdot{0,20} – 860\cdot{0,15}\]
\[ P_{A} – P_{óleo} = {1360 + 136 – 129 – 150}\]
\[ P_{A} – P_{óleo} = 1496 – 279 = 1217 \]
\[\color{blue}{P_{A} – P_{óleo} = 1217,0 kgf/m²}\]
18. ED 18 e 19
Calcular a força de Empuxo exercida pela água sobre a parede ZY e sobre a parede YX do reservatório cujo volume é igual a $\color{navy}{ 135,0 m³}$, completamente cheio, conforme figura abaixo. Considere $\color{navy}{X = 2,5 m} $e $\color{navy}{Y = 3,0 m}$. Determine também o centro de pressão nestas duas pareces.
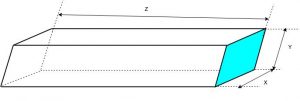
Foi nos informado o volume do reservatório e duas de suas medidas. Sabemos da geometria que o volume de um paralelogramo é \[\bbox[silver,5px,border:2px solid olive]{\color{maroon}{V = X\cdot Y\cdot Z}}\]
\[ 135,0 = 2,5\cdot{3,0}\cdot{Z}\]
\[135,0 = {7,5}\cdot{Z}\] \[{135,0\over {7,5}} = Z\] \[\color{blue}{Z = {135,0\over{7,5}}= 18 m}\]
Podemos então calcular as áreas das paredes e também seus centros de gravidade.
A parede XY, tem como área \[\color{maroon}{A_{XY} = X\cdot Y}\]
\[\color{blue}{A_{XY} = 2,5\cdot{3,0}= 7,5 m²}\]
O centro de gravidade fica na metade da altura Y, portanto$\color{navy}{ 1,5 m}$.
A parede YZ, tem como área \[\color{blue}{A_{YZ} = 3,0\cdot{18,0} =54,0 m²}\]
O centro de gravidade fica localizado também no meio da altura Y, ($\color{navy}{1,5 m}$) e na metade do comprimento Z, logo ($\color{navy}{9,0 m}$). A força de empuxo será:
\[ F_{E_{xy}}= \gamma_{H_{2}O}\cdot{1,5}\cdot{7,5}\]
\[ F_{E_{xy}} = {10}^3\cdot{1,5}\cdot{7,5} = 11250,0 kgf\]
\[\color{blue}{F_{E_{zy}} ={10}^3\cdot{1,5}\cdot{54,0} =81000,0 kgf}\]
O momento de inércia da parede XY, é \[ I_{0_{xy}} ={{ X\cdot{Y}^3}\over 12}\]
\[I_{0_{xy}} = {{2,5\cdot{3}^3}\over {12}}\]
\[\color{blue}{ I_{O_{xy}} = 5,625 km.m²}\]
O centro de pressão na parede XY é dado por:
\[h_{CP_{XY}} = 1,5 + {5,625\over {{7,5}\cdot{1,5}}}\]
\[\color{blue}{h_{CP_{XY}} = 1,5 + 0,5 = 2,0 m}\]
O momento de inércia da parede YZ, é
\[I_{O_{zy}} = {{18\cdot{3}^3}\over 12}\]
\[\color{blue}{I_{O_{zy}} = 40,5 kg.m²}\]
O centro de pressão na parede YZ, é dado por:
\[ h_{CP_{zy}} = 1,5 + {40,5\over{54\cdot{1,5}}}\]
\[\color{blue}{h_{CP_{zy}} = {1,5 + 0,5} = 2,0 m}\]
Em caso de dúvidas, entre em contato por meio de um dos canais abaixo relacionados.
Curitiba, 12 de maio de 2015 (Republicado em 25 de outubro de 2017)
Décio Adams
www.facebook.com/livros.decioadams
@AdamsDcio
Telefone: (41) 3019-4760
Celulares: (41) 9805-0732
