FI.ME-017.02 – Mecânica, Hidrostática – Tensão superficial, capilaridade, adesão superficial.
Tensão superficial.
Forças de coesão.
São forças de atração entre as moléculas de uma mesma substância. No estado sólido elas são fortes o bastante para manter as moléculas em posição definida dentro de uma rede cristalina ou mesmo amorfa. Elas não conseguem se mover de um ponto a outro da massa de matéria.
Nos líquidos elas são mais fracas, mas ainda suficientes para manter-se unidas formando uma massa. Apenas não conseguem manter uma forma própria, dependem da forma do recipiente sólido que os contenha. Essas forças de coesão são mais ou menos intensas dependendo da natureza do líquido. O líquido com um dos maiores índices de atração entre as moléculas é a água. Isso resulta da atração forte entre os polos positivos de Hidrogênio e os negativos de Oxigênio. No interior da massa líquida as atrações entre as moléculas são anuladas mutuamente pelas moléculas vizinhas.

Tensão superficial
Na superfície, ocorre um fenômeno diverso. As moléculas que estão nessa posição, não interagem atrativa ou repulsivamente com moléculas acima delas, o que gera uma espécie de “película” ou “membrana” elástica denominada Tensão Superficial. Me ocorreu que essas moléculas formam uma espécie de “cordão de isolamento”, como se dessem as mãos umas às outras, impedindo ou pelo menos dificultando o ingresso de corpos estranhos em seu interior.

Esse fenômeno é responsável por diversas consequências. Por exemplo a formação de gotas, com forma sempre esférica ou semi-esférica. Alguns insetos conseguem caminhar sobre a água por essa razão. Finos grãos de poeira, mesmo sendo mais densos que a água, não afundam. Uma agulha de costura, um clipe, objetos de aço, conseguem ser colocados de modo suave sobre a película e ficar ali flutuando. Uma bacia ou copo enchidos lentamente, conseguem reter um pouco mais água do que sua capacidade. Isso é possível por causa da tensão superficial. Se ocorrer a queda de uma gota, capaz de provocar agitação e romper a película, fará derramar uma quantidade de líquido bem maior do que o volume da gota.
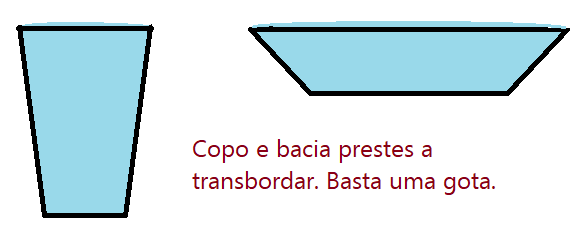

Se fecharmos uma torneira deixando apenas um filete bem fino e formos reduzindo, chegará um ponto em que irão cair gotas. A quantidade de água que sai é insuficiente para manter um filete contínuo. A tensão superficial retem a água até que a gota tenha peso suficiente para romper a tensão e cair. Isso qualquer um pode testar em sua casa, no lugar em que houver uma torneira.


As fotos foram tiradas na pia do meu banheiro. É possível observar as gotas grudadas na pia em diversas posições, inclusive na parte vertical, onde a gota fica deformada, alongando para baixo por causa da gravidade. A jarrinha cheia de água, se observamos nas bordas conseguimos ver um leve arredondamento da superfície livre que fica destacada um pouco acima das bordas.
Na natureza existem diversos insetos que, mesmo sendo mais densos do que a água, caminham sobre ela. As “patas” desses insetos são suficientemente longas para conseguir sustentação sob a ação da película de tensão superficial. Os atletas dos saltos ornamentais, sempre buscam colocar as mãos bem retas para frente, com o corpo bem alinhado no momento de entrar na água, ao final do salto. Isso diminui o “spray” de água e também minimiza o impacto no corpo. Se alguém cai ou se joga de barriga para baixo na água, pode inclusive provocar lesões sérias, dependendo da altura da queda. No mínimo a pele costuma ficar avermelhada. Esse efeito é causado pela resistência da água à entrada de corpos estranhos em seu interior. O impacto é semelhante a uma queda no solo ou em superfície sólida.
Representando a grandeza tensão superficial pela letra grega $\color{Red}{\gamma}$, podemos escrever a relação entre a força e a dimensão linear da superfície:
$$\color{Navy}{\gamma = \frac{F_{s}}{\Delta x}}$$
A força que “perfura” ou deforma a película de tensão, realiza trabalho e também podemos dizer então:
$$\color{Navy}{\gamma = \frac{\tau}{S} = \frac{F_{s}\times \Delta X}{S}}$$
As unidades são derivadas das unidades que já conhecemos de capítulos anteriores.
No SI: $\gamma = N/m \lor J/m^{2}$
No CGS: $\gamma = dyn/cm \lor erg/cm^{2}$
No MKgfS: $\gamma = kgf/m \lor kgm/m^{2}$
Existe uma expressão “energia de superfície”, referindo-se à energia por unidade de área da superfície.
Determinação da tensão superficial
A figura a seguir representa um arame dobrado em forma de U, tendo um outro pedaço móvel do mesmo arame encaixado, formando quadrilátero. Mergulhando em água com sabão (surfactante), forma-se uma película preenchendo o quadrilátero. A tensão superficial tende a trazer o firo móvel para mais perto, diminuindo a área ao valor mínimo. Uma força F, desloca o fio móvel de uma distância $\color{Sepia}{\Delta X}$, realizando um trabalho. Veja a ilustração.
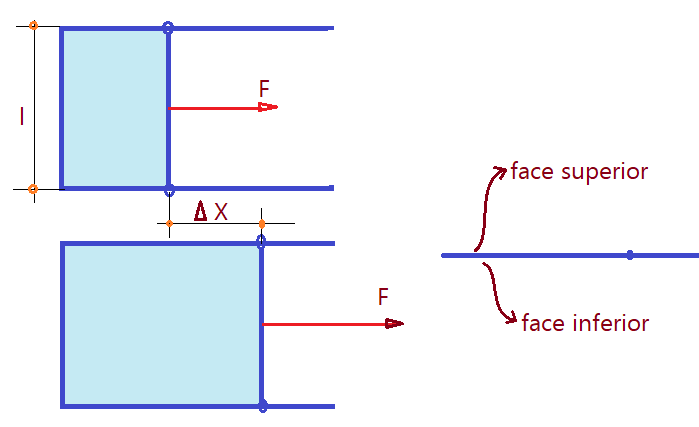
A película tem uma face superior e outra inferior, de modo que precisamos considerar a superfície em dobro. Existe uma finíssima camada de moléculas de água, aprisionadas entre duas camadas externas de surfactante, que estabilizam a película. Dessa forma, para a mistura água/sabão, teremos:
$\gamma = \frac{F\times \Delta X}{2\times l\times\Delta X}$
$$\color{Navy}{\gamma = \frac{F}{2\times l}}$$
Isolando a força nesta expressão:
$$\color{Navy}{F = 2\times\gamma\times l}$$
Tabela de alguns valores de tensão superficial.
| Líquido | Temperatura ºC | Tensão superficial em dyn/cm |
| Ácido acético | 20 | 27,6 |
| Ácido acético (40,1%}+água | 30 | 40,68 |
| Ácido Acético(10%)+água | 30 | 54,56 |
| Acetona | 20 | 23,7 |
| Éter etílico | 20 | 17 |
| Etanol | 20 | 22,27 |
| Etanol (40%)+água | 25 | 29,63 |
| Etanol (11,1%)+água | 25 | 46,03 |
| Glicerina | 20 | 63 |
| Hexano | 20 | 18,4 |
| Ácido clorídrico em solução aquosa | 20 | 65,95 |
| Isopropanol | 20 | 21,7 |
| Mercúrio | 15 | 487 |
| Álcool metílico | 20 | 22,6 |
| Octano | 20 | 21,8 |
| Solução aquosa de cloreto de sódio | 20 | 82,55 |
| Sacarose + água | 20 | 76,45 |
| Água | 0 | 75,64 |
| Água | 20 | 72,87 |
| Água | 25 | 71,97 |
| Água | 50 | 67,91 |
| Água | 100 | 58,85 |
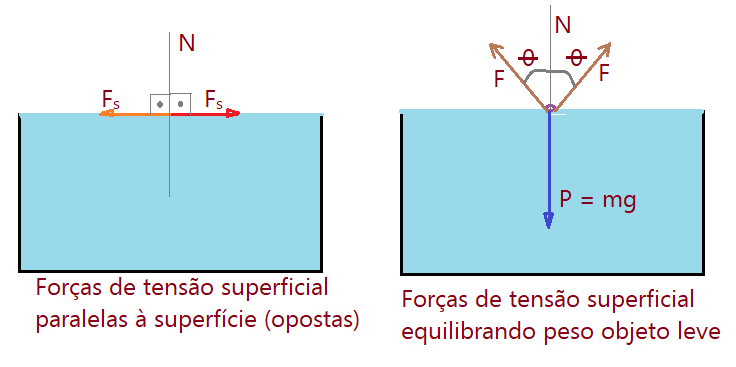
As figuras acima ilustram no primeiro caso uma superfície livre. As forças opostas, mantém o ponto em que as aplicamos na posição dentro da película superficial. Na direita, temos uma fina haste metálica (agulha ou arame), deposto sobre a superfície. As duas forças tensionais passam a atuar uma direção oblíqua, de modo a tangenciarem a superfície no ponto de sustentação do objeto. Sua resultante equilibra a força peso do objeto.
$P = F_{1}\times cos\theta + F_{2}\times cos\theta$
Como $F_{1} = F_{2}$, fica:
$$\color{Maroon}{2\gamma \times l\times cos\theta = P}$$
$$\color{Navy}{P = 2\gamma\times l\times cos\theta}$$
No limite, as duas forças agem na direção vertical ($\theta = 0^{0}$), e teremos:
$$\color{Blue}{2\times\gamma\times l = P}$$
$$\color{Navy}{P = 2\gamma l}$$
Bolhas de sabão
Uma brincadeira bastante divertida é fazer bolhas de sabão. O que isso tem a ver com o assunto em estudo?
O sabão na realidade diminui a tensão superficial da água. Isso é causado por qualquer produto denominado surfactante. A propriedade dos surfactantes no entanto permite a produção das divertidas bolhas, por estabilizar a superfície interna e externa da bolha. Quando elas tocam uma superfície horizontal uniforme, assumem uma forma parcialmente esférica, como são suscetíveis de sofrer leves deformações elásticas sem se romper. Você pode fazer a experiência em casa, com detergente ou com qualquer espécie de sabão.
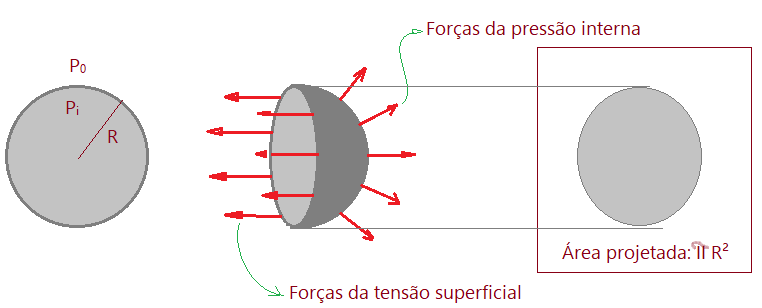
A pressão interna é maior que a externa. A tensão superficial impede a expansão além do limite. Tratando-se de pressão manométrica, consideramos a pressão externa nula: $P_{o} = 0$
$$\color{Maroon}{\sum F = 0}$$
$2\gamma{2\pi R} = P_{i}(\pi R^{2})$$\Leftrightarrow$$4\gamma = P_{i} R$
$$\color{Navy}{P_{i}=\frac{4\gamma}{R}}$$
$$\color{Blue}{P_{i} – P_{o} = \frac{4\gamma}{R}}$$
Diferença de pressão em uma gota
Em uma gota existe apenas uma superfície, a externa. Por essa razão a diferença de pressão é somente a metade da bolha de mesma dimensão com o mesmo líquido.
$$\color{Maroon}{P_{i} – P_{o} = \frac{2\gamma}{R}}$$
Capilaridade
As forças atrativas maiores ou menores conferem aos líquidos algumas propriedades que diferem entre eles. Se usarmos dois bastões de vidro e os mergulharmos em água e outro em mercúrio. Quando os retiramos, percebemos que a água deixou o bastão molhado. Algumas moléculas do líquido ficam aderentes ao sólido. Já o mercúrio não se comporta assim. A intensa força de coesão entre suas moléculas impede o líquido de molhar o bastão.
A combinação da tensão superficial e a capacidade de “molhar” ou não o sólido, produz o efeito da capilaridade. Um tubo capilar introduzido na água, resultará numa elevação do líquido dentro do tubo, no que denominamos elevação capilar. No mercúrio, um tubo semelhante irá apresentar uma depressão capilar, isto é, o líquido no interior do tubo ficará um pouco abaixo da superfície livre.
Isso também é perceptível em provetas de vidro transparente. A água irá ter uma leve elevação nas bordas, formando o que se denomina menisco côncavo. Se usarmos o mercúrio, ocorrerá o contrário. Nas bordas haverá uma leve curvatura para baixo, formando o que denominamos menisco convexo. Observe as ilustrações das figuras.
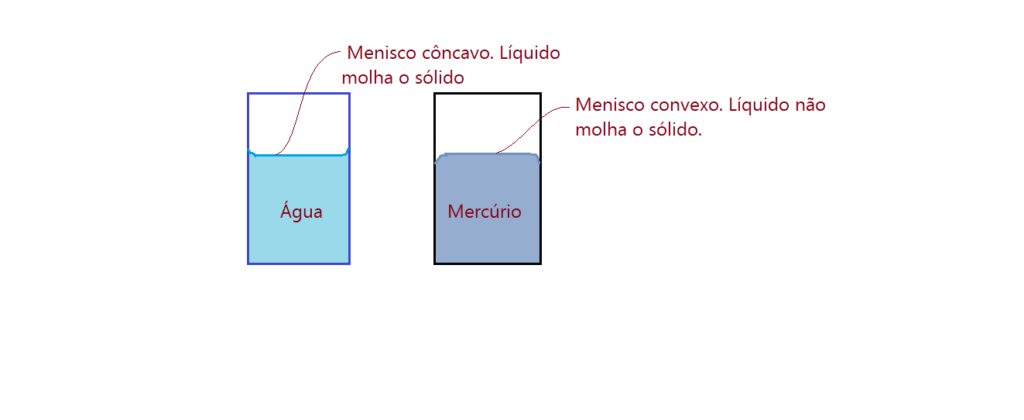
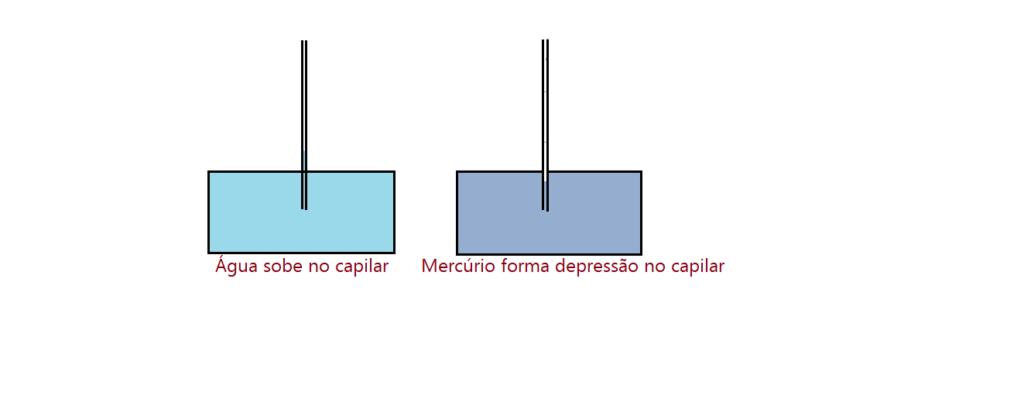
Isso explica o fato de haver elevação de umidade nas paredes de alvenaria, especialmente nos tijolos, cujo material é poroso, onde ocorre o fenômeno da capilaridade. Isso levou os construtores a usar uma camada de material isolante entre o alicerce e as paredes. Dessa forma ocorre o impedimento da subida de umidade nas paredes, o que causa danos ao reboco e pintura, além de deixar os recintos pouco saudáveis para seus ocupantes.
Na capilaridade, a combinação das forças tensionais, de coesão e gravitacionais, determina a altura de equilíbrio da elevação ou depressão.
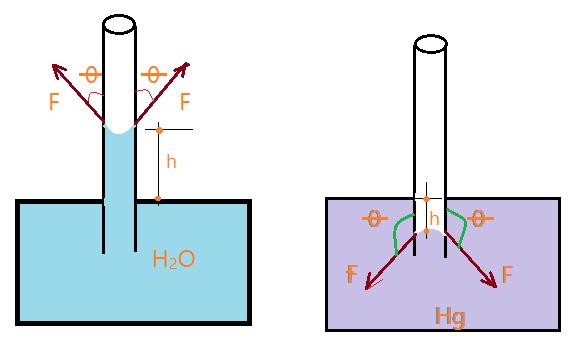
Nas figuras observamos que as forças que elevam ou deprimem são similares às que atuam sobre um objeto que flutua sobre o líquido, mesmo sendo mais denso.
$$\color{Maroon}{P = mg = \mu g (\pi R^{2} h)}$$
O comprimento é o círculo do tubo capilar: $2 l = 2\pi R$
$$\color{Brown}{F_{i} = 2\pi R\gamma cos\theta}$$
Igualando as duas forças:
$\mu g (\pi R^{2} h) = 2\pi R\gamma cos\theta $$\Leftrightarrow$$\mu g R h = 2\gamma cos\theta$
$$\color{Navy}{h = \frac{2\gamma}{\mu g R}\cos\theta}$$
Para o caso da depressão, teremos o ângulo $\theta$ maior que $90^{0}$, o que irá resultar em um valor $h < 0$.
Exercícios para resolver
01. Um surfactante é uma substância que atua sobre outra para alterar a:
( )a) Osmolaridade;
( )b) Tensão superficial;
( )c) Eletroforese;
( )d) Viscosidade;
( )e) Pressão osmótica.
02. A tensão superficial dos líquidos depende diretamente de processos de interação entre as moléculas, como ligação de hidrogênio, por exemplo. Qual das substâncias abaixo tem maior tensão superficial?
( )a) benzeno;
( )b) octano;
( )c) álcool etílico;
() d) tetracloreto de carbono;
( )e) ácido etanoico.
03. Alguém, usando um loop circular de arame e um recipiente com água e sabão, produz uma bolha com raio de $\color{Sepia}{R_{1}=1\,mm}$. A tensão superficial da mistura é $\color{Sepia}{\gamma = 2,5\times 10^{-2}\,N/m}$.
(a) Determine a diferença de pressão entre o interior e o
exterior da bolha;
(b) A mesma mistura de água e sabão é usada para produzir uma gota cujo raio é a metade do da bolha, $\color{Sepia}{R_{2}=0,5\,mm}$. Encontre a diferença de pressão entre o interior e o exterior da gota.
04. Uma agulha de $\color{Sepia}{l =3,2\,cm}$ de comprimento é colocada delicadamente sobre a água em um béquer ($\color{Sepia}{\gamma = 0,073 N/m}$). Se não for muito pesada a agulha não afundará. Qual o máximo peso de agulha que pode ser usada nesta
demonstração?
05. Uma gota de água se forma sobre uma folha durante a madrugada, por causa da deposição de orvalho. Seu raio é $\color{Sepia}{R=1,5\,mm}$. Determine a diferença de pressão entre o interior e o exterior da gota, sabendo que a tensão superficial da água pura é $\color{Sepia}{\gamma=75,65\times 10^{-3}\,N/m}$.
06. Um tubo de vidro, mede $\color{Sepia}{D=1,80mm}$ em seu diâmetro interno e sua extremidade é introduzida em um recipiente contendo solução de sacarose + água, cuja tensão superficial é $\color{Sepia}{\gamma = 76,45\,dyn/cm}$. A solução molha o sólido e se forma um menisco côncavo. Em suas bordas a linha tangente ao menisco formam ângulo se $\color{Sepia}{\theta = 45^{0}}$. Determine a altura da elevação capilar. O valor da densidade absoluta é $\color{Sepia}{\mu= 1,04.10^{3}\,kg/m^{3}}$ e a aceleração da gravidade valr $\color{Sepia}{g = 9,81\,m/s^{2}}$.
07. Um tubo de vidro, cujo diâmetro interno mede $\color{Sepia}{D = 1,6\,mm}$, tem sua extremidade introduzida num recipiente com mercúrio metálico. A massa específica do mercúrio é $\color{Sepia}{\mu_{Hg}=13,6\,g/cm^{3}}$, a gravidade mede $\color{Sepia}{g=10,0\,m/s^{2}}$. Se a tensão superficial do líquido é $\color{Sepia}{\gamma = 487\,dyn/cm}$ e as bordas do menisco convexo formado formam um ângulo de $\color{Sepia}{\theta= 150^{0}}$. Determinar a altura da depressão capilar formada.
08. Uma bolha de sabão mede $\color{Sepia}{R_{1} = 2,5\,cm}$. Sendo a mistura água sabão tal que sua tensão superficial vale $\color{Sepia}{\gamma=30,26\,dyn/cm}$. Determine a diferença entre a pressão interna e externa para essa bolha. Se for produzida uma gota dessa mistura, cujo raio seja $\color{Sepia}{R_{2} = 0,25\,cm}$, qual será a diferença entre a pressão interna e externa.
09. Um fino anel metálico é depositado suavemente sobre a superfície livre de uma bacia cheia de água limpa. Se o raio do anel é $\color{Sepia}{R=2,5\,cm}$, qual pode ser o peso máximo que o anel poderá ter para ficar flutuando? Sabe-se que $\color{Sepia}{\gamma_{H_{2}O}=75,65\,dyn/cm}$.
10. Uma mistura de água com detergente possui $\color{Sepia}{\gamma=35,4\,dyn/cm}$. Uma bolha dessa mistura tem raio de $\color{Sepia}{R_{1}=3,0\,cm}$. Qual é o valor da diferença de pressão interna e externa dessa bolha? Uma gota dessa mistura, tem raio $\color{Sepia}{R_{2} = 1,50\,mm}$, determine a diferença entre as pressões interna e externa.
Se tiver dúvidas, peça ajuda por um dos canais abaixo para esclarecer tudo. Sempre poderá contar comigo.
Curitiba, 14 de setembro de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760 Celular e WhatsApp: (41) 99805-0732
