Física – Ótica – Ótica Geométrica.
Prisma ótico
Quem deu início a essas experiências foi Sir Isaac Newton, matemático e físico inglês no final do século XVII, início do XVIII. Foi, junto com Leibniz, embora de forma independente, o responsável pelo desenvolvimento dos fundamentos do que hoje é denominado Cálculo Diferencial e Integral.
Contradizendo a imensa maioria dos pensadores entendidos no assunto, Isaac fez experimentos e testou todas as variações possíveis. Durante décadas foi contestado e esteve à beira de desistir da continuação de suas pesquisas. Seu verdadeiro valor foi reconhecido muito mais após sua morte do que em vida.
Já se sabia usar as lentes esféricas, espelhos esféricos côncavos e convexos, mas era voz corrente que a luz era uma onda, sendo as cores provocadas pela perturbação que a onda provocava nos meios em que se propagava.
Recluso em seu quarto, Newton fez uma experiência inédita. Fez um fino feixe de luz que penetrava por um orifício, incidir sobre uma das faces de uma peça de vidro, com as faces planas, mas não paralelas. Qual não foi sua surpresa ao verificar que na segunda face emergia um pincel de luzes coloridas. Conta uma lenda de que ele teria exclamado “spectrum”, o que que significa “fantasma” na língua latina, usada pelos filósofos, matemáticos e pensadores em geral naquele tempo. Hoje podemos reproduzir essa experiência em qualquer laboratório minimamente equipado ou mesmo em nossa própria casa, com um pouco de imaginação e criatividade. Observemos a figura a seguir.

A refração, como vimos anteriormente, ocorre quando a luz ultrapassa a superfície de separação entre dois meios, mudando de velocidade. A experiência de Newton demonstra que a variação de velocidade é diferente para as ondas de cores diferentes. Isso ocasiona um desvio maior para as cores que sofrem maior variação de velocidade. Em consequência os ângulos de incidência na segunda face, são diferentes entre si e assim a nova refração provoca um aumento no desvio sofrido pela luz. Dessa forma aparecem os pontos ou faixas de luzes das diversas cores do arco íris. Os desvios são crescentes a começar da cor vermelha, laranja, amarela, verde, azul, anil e violeta. Maior desvio, maior variação de velocidade. Hoje sabemos que o desvio é relacionado com o comprimento de onda, sendo inversamente proporcional.
Tomemos um raio de luz monocromático, isto é de uma cor determinada e o façamos incidir sobre uma face de um prisma ótico. Vamos analisar o desvio angular que ele irá sofrer até emergir na segunda face.
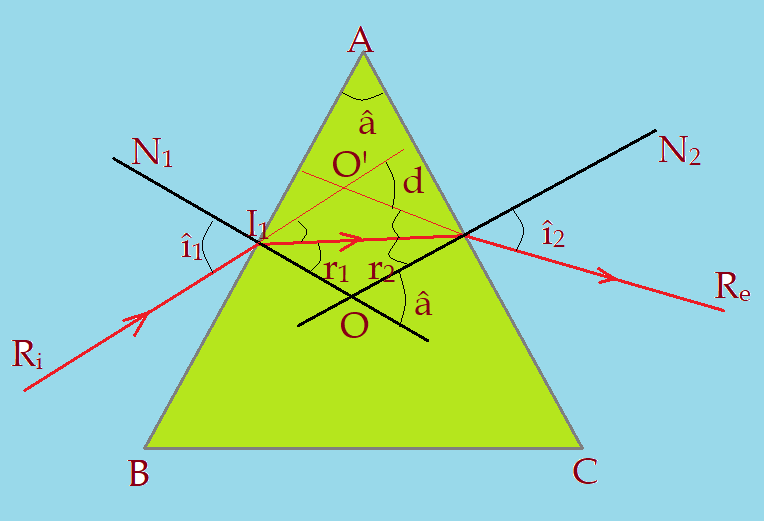
As duas normais $N_{1}$ e $N_{2}$, formam um ângulo interno que é parte do triângulo $\Delta{(I_{1}I_{2}OI_{1})}$. O angulo externo adjacente é igual ao ângulo de refringência. Seus lados são perpendiculares entre si respectivamente. A geometria nos ensina que a soma dos ângulos internos de um triângulo é igual a $180^0$. Dois ângulos adjacentes, onde os lados não comuns são segmentos consecutivos, somam também $180^0$, isto é, são suplementares.
$\hat{r_{1}} + \hat{r_{2}} + (180^0 – â) = 180^0$
$\hat{r_{1}} + \hat{r_{2}} = â + 180^0 – 180^0$
$\hat{r_{1}} + \hat{r_{2}} =â$
$â = \hat{r}_{1}+\hat{r}_{2}$ (I)
A intercessão dos prolongamentos do raio incidente na primeira face e do emergente na segunda face, com os pontos $I_{1}$ e $I_{2}$, formam o triângulo $\Delta{(I_{1}I_{2}O’I_{1})}$, onde podemos escrever:
$î_{1} – \hat{r_{1}} + î_{2} – \hat{r_{2}} + 180^0 – \hat{d} = 180^0$
$î_{1} + î_{2} -(\hat{r_{1}} + \hat{r_{2}}) = \hat{d} + 180^0 – 180^0$
$î_{1} + î_{2} -\underbrace{(\hat{r_{1}} + \hat{r_{2}})} = \hat{d}$ (II)
Substituindo (I) em (II):
$î_{1} + î_{2} – â = \hat{d}$
$\hat{d} = î_{1} + î_{2} – â$
Os prismas mais comuns são triangulares em suas faces paralelas. As faces que funcionam como superfícies refratoras, são as outras faces retangulares. Vejamos a figura a seguir:
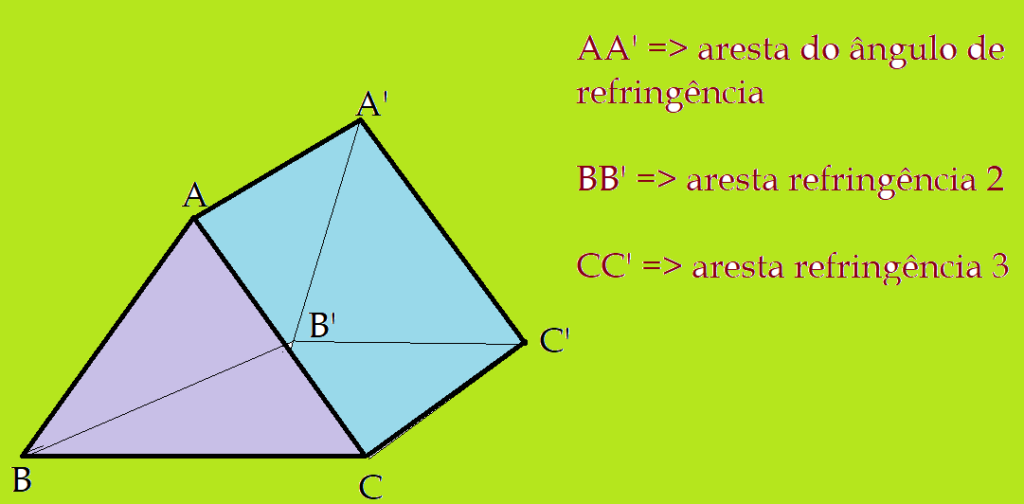
Na figura vemos que a aresta $\overline{AA’}$ está colocada na posição superior e iriam funcionar como superfícies refratoras as faces ${AA’C’CA}$ e ${AA’B’BA}$. Se desejarmos usar outro vértice, bastará inverter a posição do prisma. Para efeito de representação gráfica dos fenômenos de refração no interior do prisma, usamos sempre um corte transversal, que resulta em um triângulo. Esse triângulo pode ser equilátero, retângulo, isósceles, escaleno, dependendo das finalidades de sua aplicação. Determinados efeitos desejados são obtidos com determinadas formas de prismas.
Prisma de reflexão total
Em um prisma de vidro, com secção transversal em forma de triângulo retângulo isósceles, imerso no ar, pode acontecer a seguinte situação. Um raio monocromático incide normalmente sobre uma face, se refrata sem desviar e sofre reflexão interna na segunda face (45^0}. Torna a se refletir totalmente na terceira face e emerge na primeira, apenas deslocado para um lado, mas paralelo ao raio incidente.
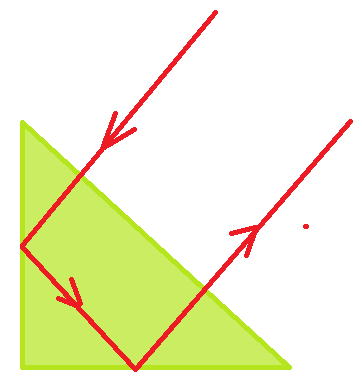
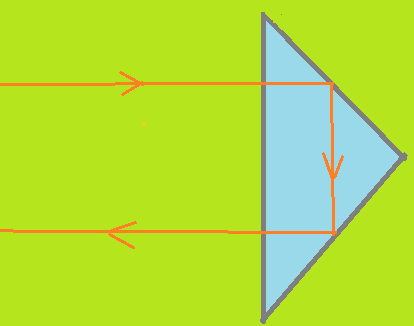
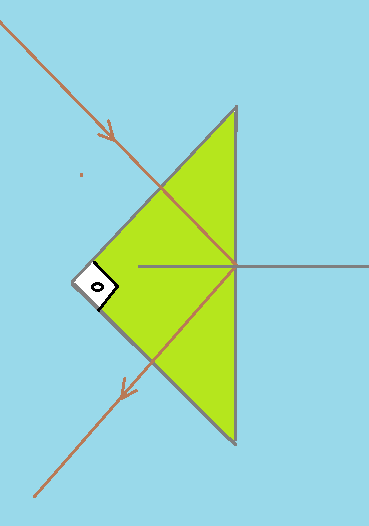
Os prismas de reflexão total tem enorme aplicação nos instrumentos óticos. Eles substituem, em inúmeras situações, os espelhos metálicos, uma vez que a reflexão total fornece um feixe refletido, de intensidade superior ao fornecido pelos espelhos. Em outras palavras o poder refletor é mais elevado. Assim usam-se em binóculos, telescópios, microscópios, conjunto ótico de câmeras fotográficas, no interior de periscópios e instrumentos de observação diversos que assim passam a fornecer imagens mais nítidas.
Obs.: Os melhores espelhos metálicos não alcançam um poder refletor que se iguale a 90% da luz incidente. Já a reflexão total em um prisma ótico ultrapassa esse percentual. Isso representa um ganho significativo na nitidez de imagens fornecidas por equipamentos óticos por conta do uso dos prismas de reflexão total. Eis a razão de sua utilidade.
Condições de desvio mínimo
Existem situações em que é desejável que o desvio produzido por um prisma, na direção de propagação de um raio luminoso monocromático seja o menor possível. Se observarmos detalhadamente o percurso do raio ao atravessar o prisma, sendo o mesmo imerso num outro meio transparente, isótropo e homogêneo, veremos que, quanto mais as medidas dos ângulos de emergência $î_{2}$ e incidência $î_{1}$ se aproximarem da igualdade, também estaremos tendo $\hat{r}_{1}$ e $\hat{r}_{2}$ se aproximando da igualdade. Na situação limite teremos o desvio reduzido ao menor valor possível para um determinado prisma. Nessa condição, o percurso do raio luminoso no interior do prisma terá direção paralela ao segmento de reta representado pela base da seção do prisma. Iremos notar também que essa condição fica mais fácil de realizar na medida em que o ângulo de refringência do prisma for ficando menor.
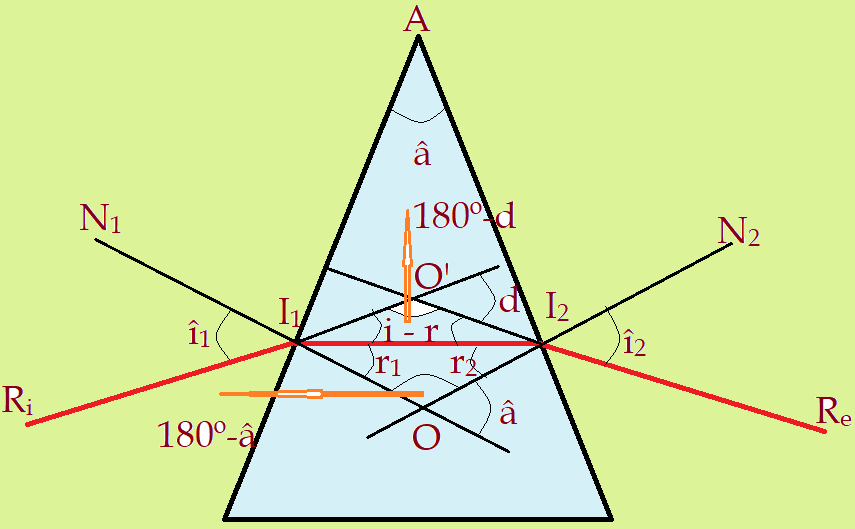
Vimos acima que:
$ â = \hat{r}_{1} + \hat{r}_{2}$
$\hat{d} = î_{1} + î_{2} – â$
Na condição de desvio mínimo iremos ter:
$â =\hat{r} + \hat{r}$
$ â = 2\cdot{\hat{r}}$ (I)
$\hat{d}_{m} = 2\cdot i – â$ (II)
Podemos fundir as duas expressões em uma obtendo:
$\hat{d_{m}} = 2\cdot i – 2\cdot\hat{r}$$\Leftrightarrow$$ \hat{d_{m}} = 2\cdot{(i – r)}$
É importante notar que o ângulo $180^0 – â$ é formado pelas retas normais às faces do prisma nos pontos de incidência e emergência do raio luminoso. O ângulo $180^0 – \hat{d}$ é formado pelos prolongamentos do raio incidente $R_{i}$ e emergente $R_{e}$. Na proporção que o ângulo de refringência diminui, o ângulo formado pelas retas normais, interno ao triângulo $\Delta{(I_{1}I_{2}OI_{1})}$ aumenta. Isso implica em que os ângulos de refração interna irão diminuir. Do mesmo modo os ângulos de incidência/emergência diminuem levando a um desvio cada vez menor.
Vamos aplicar o que aprendemos?
- Um prisma de base triangular, é feito de vidro com índice de refração $n_{2} = \sqrt{2}$. Um raio de luz monocromática se propaga no ar e atinge uma das faces do prisma segundo um ângulo $î_{1} = 30^0$. Determine o ângulo refração na primeira face, o ângulo de incidência na segunda face, o ângulo de emergência e o desvio angular. Sabendo que o ângulo de refringência do prisma é $â = 60^0$.
Para determinar a resposta à primeira questão, usaremos a Lei de Snell:
${{sen(î_{1})\over sen(\hat{r}_{1})}= {{n_{2}}\over{n_{1}}}}$
Temos que $î_{1} = 30^0$
$n_{2} = \sqrt{2}$
$n_{1}\simeq 1$
${{sen (30^0)\over sen \hat{r}_{1}} = {{\sqrt{2}\over 1}}}$
${1\over 2}\cdot 1 = {\sqrt{2}\cdot sen\hat{r}_{1}}$$\Leftrightarrow$${1\over2}\cdot {1\over\sqrt{2}}= sen\hat{r}_{1}$
${1\over 2}\cdot{1\over\sqrt{2}}\cdot{\sqrt{2}\over\sqrt{2}} =\hat{r}_{1}$$\Leftrightarrow$$ {\sqrt{2}\over 4} = sen\hat{r}_{1}$
$sen\hat{r}_{1}\simeq 0,35$$\Leftrightarrow$ $\hat{r}_{1} \simeq 20,5^0$
Se $â = \hat{r}_{1} + \hat{r}_{2}$
$â = 60^0$
$ 60^0 = 20,5^0 + \hat{r}_{2}$ $\Leftrightarrow$$ \hat{r}_{2} = 39,5^0$
Na segunda face a luz passa do meio mais refringente (prisma) novamente para o ar, meio menos refringente.
${sen\hat{r}_{2}\over sen î_{2}} = {n_{1}\over n_{2}}$$\Leftrightarrow$${sen(39,5^0)\over sen î_{2}} = {1\over\sqrt{2}}$
${0,636\cdot\sqrt{2}} = {1\cdot sen î_{2}}$$\Leftrightarrow$$sen î_{2} = {0,636\cdot\sqrt{2}}$
$sen î_{2}\simeq 0,90$ $\Leftrightarrow$$î_{2} \simeq 64,2^0$
O desvio angular será: $\hat{d} = î_{1} + î_{2} – â$
$\hat{d} = 30^0 + 64,2^0 – 60^0$$\Leftrightarrow$$\hat{d} = 34,2^0$
2. Um prisma triangular, cujo índice de refração é $n_{2}=\sqrt{3}$, está imerso em um meio gasoso, cujo índice de refração é $n_{1} = \sqrt{2}$. Um raio de luz monocromática propaga-se no meio gasoso e incide na face do prisma sob um ângulo $î_{1} = 30^0$. Sendo o ângulo de refringência de $â = 45^0$, determinar o ângulo de refração na primeira face, o ângulo de incidência ($\hat{r}_{2}$) e o desvio angular do raio luminoso.
${{sen î_{1}\over sen\hat{r}_{1}} = {n_{2}\over n_{1}}}$
${sen 30^0\over sen\hat{r}_{1}} = {\sqrt{3}\over\sqrt{2}}$$\Leftrightarrow$${{{1\over2}\over sen\hat{r}_{1}} = {{\sqrt{3}\cdot\sqrt{2}}\over\sqrt{2}^2}}$
${{sen\hat{r}_{1}} = {\sqrt{6}\over 6}}$
$sen\hat{r}_{1}\simeq 0,408$
$\hat{r}_{1}\simeq 24,1^0$
$â = \hat{r}_{1} + \hat{r}_{2}$$\Leftrightarrow$$45^0 = 24,1^0 + \hat{r}_{2}$
$\hat{r}_{2} = 45^0 – 24,1^0$$\Leftrightarrow$$\hat{r}_{2} = 20,9^0$
${sen\hat{r}_{2}\over sen î_{2}} = {n_{2}\over n_{1}}$
${sen 45^0\over sen î_{2}} = \sqrt{3}\over\sqrt{2}$
${{{\sqrt{2}\over2}\cdot\sqrt{2}}\over\sqrt{3}} = {sen î_{2}}$$\Leftrightarrow$${{{\sqrt{4}\cdot\sqrt{3}}\over\sqrt{3}^2} = {sen î_{2}}}$
$senî_{2} = {\sqrt{3}\over 3}$$\Leftrightarrow$$sen î_{2} = 0,577$
$î_{2}\simeq 35,24^0$
$\hat{d} = î_{1} + î_{2} – â$$\Leftrightarrow$$\hat{d} = 30^0 + 35,24^0 – 45^0$
${\hat{d}\simeq 65,24^0 – 45^0 \simeq 20,24^0}$
3. Um raio de luz monocromática atravessa um prisma ótico triangular, sofrendo desvio mínimo. Se o ângulo de refringência do prisma é $â = 60^0$ e o índice de refração do prisma é $n_{2} = 1,6$ e está imerso no ar $n_{1}\simeq 1$,determine os ângulos de refração e incidência interna do prisma, os ângulos de incidência e refração externos, além do desvio mínimo que o raio sofre.
$â = 2\cdot r$
$60^0 = 2r$$\Leftrightarrow$$ r = {60^0\over 2}$
$ r = 30^0$
${senî\over senr} = {n_{2}\over n_{1}}$$\Leftrightarrow$${sen i \over sen 30^0} = {{1,6}\over 1}$
$senî = {{1,6}\cdot{1}\over 2}$$\Leftrightarrow$$sen î = 0,8$
$i = 53,1^0$
$\hat{d}_{m} = 2\cdot{(i – r)}$$\Leftrightarrow$$\hat{d}_{m} = 2\cdot{(53,1^0 – 30^0)}$
$\hat{d}_{m} = 23,1^0$
Que tal caminhar um pouco só!
- Um raio monocromático propaga-se no ar e incide sobre uma das faces de um prisma triangular de ângulo de refringência $\hat{a} = 30^{0}$, por um ângulo $\hat{i}_{1} = 40^{0}$. Determine os ângulos de refração e incidência interna, o ângulo de emergência e o desvio angular sofrido.
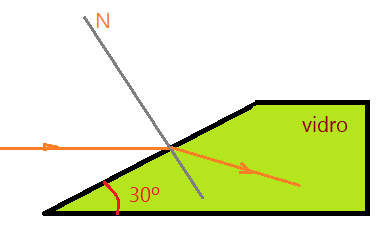
- A figura abaixo mostra um raio monocromático de luz que incide horizontalmente sobre um bloco de vidro. Sabendo-se que o bloco está imerso no ar ($n_{ar} = 1$) e que o índice de refração absoluto do vidro vale $n_{vid}=\frac{\sqrt{6}}{2}$ , ângulo de refração na refração na 1ª face do bloco de vidro vale:
| Ângulo | seno | cosseno |
| $0^{0}$ | $0$ | $1$ |
| $30^{0}$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ |
| $45^{0}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ |
| $60^{0}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ |
| $90^{0}$ | $1$ | $0$ |
( )a) $0^{0}$;
( )b) $30^{0}$;
( )c) $45^{0}$;
( )d) $60^{0}$;
( )e) $90^{0}$.
3. (UEL – PR) No esquema adiante considere:
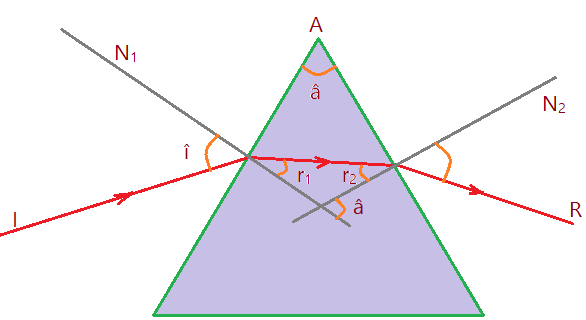
I – raio incidente;
$N_{1}$ e $N_{2}$ – normais às faces do prisma;
$\hat{r}_{1}$ – ângulo de refração na primeira face;
$\hat{r}_{2}$ – ângulo de incidência na segunda face;
$\hat{a}$ – ângulo do prisma = $60^{0}$.
Considerando as indicações do esquema, é correta a relação:
( )a) $\hat{r}_{1} – \hat{r}_{2} = \hat{q}$;
( )b) $\hat{r}_{1} + \hat{r}_{2} = \hat{q}$;
( )c) $\hat{r}_{1} + \hat{r}_{2} = 90^{0} – \hat{q}$;
( )d) $\hat{r}_{1} – \hat{r}_{2} = 90^{0} – \hat{q}$;
( )e) $2\times(\hat{r}_{1} + \hat{r}_{2}) = \hat{q}$.
4. (UEL – LONDRINA) – A figura abaixo representa um raio de luz que atravessa um prisma. O desvio sofrido por esse raio de luz, em graus, vale:
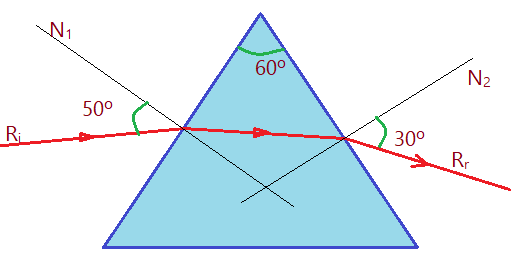
( )a) $20^{0}$
( )b) $30^{0}$;
( )c) $45^{0}$;
( )d) $60^{0}$;
( )e) $90^{0}$.
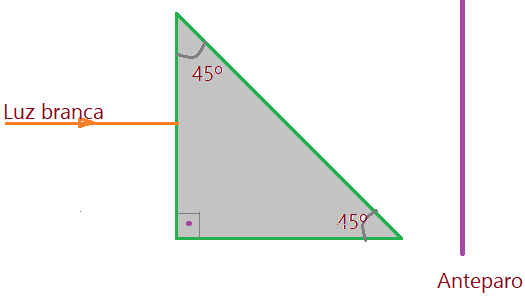
5. (FUVEST) – Um pincel de luz branca incide perpendicularmente em uma das faces menores de um prisma, cuja secção principal é um triângulo retângulo e isósceles.
O prisma está imerso no ar e é constituído de um material transparente, que apresenta, para as sete radiações monocromáticas caracterizadas por sua cor, o índice de refração absoluto n, indicado na tabela abaixo:
violeta …………………… 1,48
anil ……………………….. 1,46
azul ……………………….. 1,44
verde …………………….. 1,42
amarelo …………………. 1,40
alaranjado ……………… 1,39
vermelho ……………….. 1,38
Valores numéricos de alguns senos:
$sen(30^{0}) = \frac{1}{2}$; $sen(45^{0}) = \frac{\sqrt{2}}{2}$ e $sen(60^{0}) = \frac{sqrt{3}}{2}$
Observa-se que nem todas as radiações atingem um anteparo destinado a receber o espectro. Quais as cores recebidas no anteparo? Justifique sua resposta.
6. A respeito do desvio experimentado por um raio de luz ao penetrar em um prisma, podemos afirmar:
( )a) é independente da radiação monocromática;
( )b) é função crescente do ângulo de incidência;
( )c) é função crescente do ângulo de refringência;
( )d) é independente do índice de refração relativo do prisma;
( )e) N.d.a.
7. (ITA) – O Método de Desvio Mínimo, para a medida do índice de refração, $n$, de um material transparente, em relação ao ar, consiste em se medir o desvio mínimo $\hat{\delta}$ de um feixe estreito de luz que atravessa um prisma feito desse material. Para que esse método possa ser aplicado (isto é, para que se tenha um feixe emergente), o ângulo $\hat{A}$ do prisma deve ser menor que:
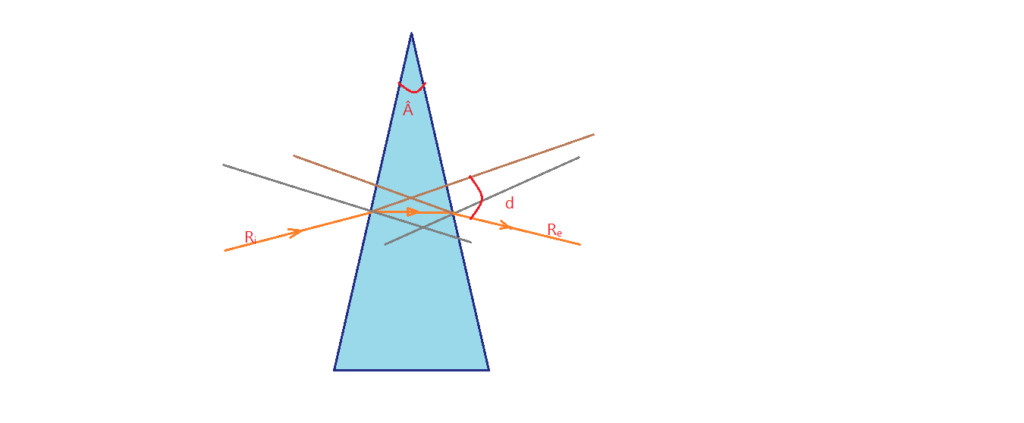
( )a) arcsen (n);
( )b) 2 arcsen (1/n);
( )c) 0,5 arcsen (1/n);
( )d) arcsen (1/n);
( )e) p/2.
8. (MACKENZIE) – Dispõe-se de um prisma óptico cuja secção transversal é um triângulo equilátero. Ao ser colocado num meio de índice de refração absoluto , um raio luminoso, que incide numa secção principal sob um ângulo de $30^{0}$ com uma das faces, emerge perpendicularmente à outra. Neste caso, podemos afirmar que:
( )a) O índice de refração absoluto do material do prisma é $\frac{\sqrt{3}}{3}$;
( )b) O índice de refração absoluto do material do prisma é $\sqrt{3}$;
( )c) O desvio sofrido pelo raio é de $90^{0}$;
( )d) O desvio sofrido pelo raio é de $60^{0}$;
( )e) O desvio sofrido pelo raio é de $30^{0}$.
09. (UEPG – RS) – Se fizermos incidir sobre um prisma um fino feixe de luz branca, veremos emergir do outro lado um feixe de luz colorido e mais espesso, que nos lembra um arco-íris. Com relação a esse fenômeno, que é chamado de dispersão da luz, assinale a alternativa que contém uma afirmação incorreta:
( )a) A luz branca é uma combinação das cores do espectro;
( )b) O índice de refração absoluto do prisma é único para todas as cores;
( )c) As cores do espectro são puras;
( )d) O índice de refração absoluto do prisma é diferente e maior para luz violeta do que para luz vermelha;
( )e) O índice de refração absoluto do prisma é maior para luz violeta do que para luz vermelha.
10. (UF VIÇOSA) – Ao incidirmos um feixe de luz branca sobre um prisma, observamos a dispersão da luz no feixe emergente, sendo que a cor violeta sofre o maior desvio e a vermelha, o menor. Analise as seguintes afirmações:
I. O índice de refração absoluto do vidro é maior para a luz violeta;
II. O índice de refração absoluto do vidro é maior para a luz vermelha;
III. O módulo da velocidade da luz violeta dentro do vidro é maior que o da luz vermelha;
IV. O módulo da velocidade da luz vermelha dentro do vidro é maior que o da violeta;
V. As velocidades das luzes vermelha e violeta têm módulos iguais dentro do vidro.
São verdadeiras:
( )a) II e IV;
( )b) I e V;
( )c) I e III;
( )d) I e IV;
( )e) II e III.
11. (FUVEST) – Um feixe de luz é uma mistura de três cores: verde, vermelho e azul. Ele incide, conforme indicado na figura, sobre o prisma de material transparente, com índice de refração crescente com a frequência. Após atravessar o prisma, a luz atinge um filme para fotografia a cores que, ao ser revelado, mostra três manchas coloridas.
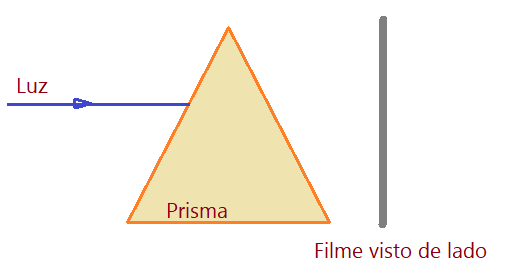
De cima para baixo, as cores dessas manchas são, respectivamente:
( )a) verde, vermelho e azul;
( )b) vermelho, azul e verde;
( )c) azul, vermelho e verde;
( )d) verde, azul e vermelho;
( )e) vermelho, verde e azul.
12. (UEL-PR) – A figura abaixo representa um raio de luz que atravessa um prisma. O desvio sofrido por esse raio de luz, em graus, vale:
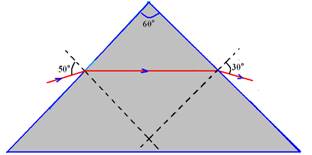
( )a) 20;
( )b) 30;
( )c) 50;
( )d) 60;
( )e) 90.
13. (MACKENZIE-SP) – Um raio luminoso incide perpendicularmente a uma das faces de um prisma de vidro ($\color{Maroon}{n_{vid}=\frac{\sqrt{3}}{2}}$), imerso no ar ($\color{Maroon}{n_{ar}=1}$), e emerge rasante à outra face. O ângulo de refringência A desse prisma é:
( )a) $15^{0}$;
( )b) $30^{0}$;
( )c) $40^{0}$;
( )d) $45^{0}$;
( )e) $60^{0}$.
14. (PUC-SP) – Um prisma de vidro, cujo ângulo de refringência é $\color{Maroon}{A =60^{0}}$, está imerso no ar. Um raio de luz monocromática incide em uma das faces do prisma sob ângulo de $\color{Maroon}{\hat{i}_{1} = 45^{0}}$ e, em seguida, na segunda face sob ângulo de $\color{Maroon}{\hat{r}_{2}= 30}0}$, como está representado no esquema.
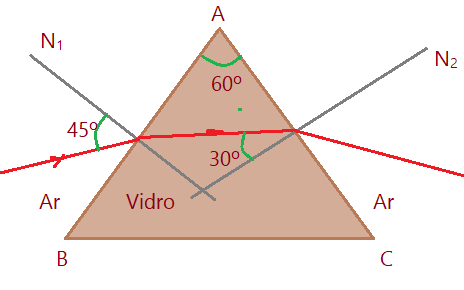
Calcule o índice de refração do vidro em relação ao ar, para essa luz monocromática.
15. (PUC-SP) – Um raio de luz monocromática incide perpendicularmente em uma das faces de um prisma equilátero e emerge de forma rasante pela outra face. Considerando $\color{Maroon}{n= 1,73}$ e supondo o prisma imerso no ar, cujo índice de refração é $\color{Maroon}{n_{ar}=1}$, o índice de refração do material que constitui o prisma será, aproximadamente:
( )a) 0,08;
( )b) 1,15;
( )c) 2,00;
( )d) 1,41;
( )e) 2,82.
16. (ITA-SP) – Um prisma de vidro, de índice de refração n=, tem por secção normal um triângulo retângulo isósceles ABC no plano vertical. O volume de secção transversal ABD é mantido cheio de um líquido de índice de refração n’=. Um raio incide normalmente à face transparente da parede vertical BD e atravessa o líquido.
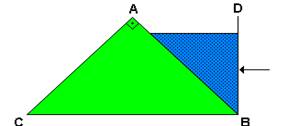
Considere as seguintes afirmações:
I) O raio luminoso não penetrará no prisma;
II) O ângulo de refração na face AB é de $45^{0}$;
III) O raio emerge do prisma pela face AC com ângulo de refração de $45^{0}$;
IV) O raio emergente definitivo é paralelo ao raio incidente em BD.
Das afirmativas mencionadas, é (são) correta (s):
( )a) Apenas I;
( )b) Apenas I e IV;
( )c) Apenas II e III;
( )d) Apenas III e IV;
( )e) II, III e IV.
Se existirem dúvidas sobre a solução, não deixe de procurar esclarecimento comigo. Os canais são os listados abaixo.
Curitiba, 02 de novembro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
