Física – Ótica Geométrica.

By decioadams in Física, Ótica, Ótica geométrica, Refração da luz 20 de outubro de 2019

Profundidade aparente de um meio

Existe uma situação prática bastante interessante. Imaginemo-nos em um pequeno barco em um lago ou rio, tendo em nossas mãos um acro com sua respectiva flecha. O objetivo é alvejar um peixe que se pode ver na água limpa, numa determinada posição. Onde devemos apontar nossa flecha se quisermos ter uma chance de acertar no peixe?

Os nossos ancestrais perceberam isso intuitivamente, mesmo sem dispor dos conhecimentos de ótica que hoje temos. Vemos o peixe por causa da luz que nele se reflete e chega aos nossos olhos. Mas não podemos esquecer que o peixe está na água e a luz irá atravessar o dioptro água/ar, onde ocorrerá uma mudança de direção. A luz estará passando de um meio mais refringente para um menos refringente $\color{Maroon}{n_{H_{2}O} > n_{ar}}$ e se afastará da normal. Vejamos a ilustração.

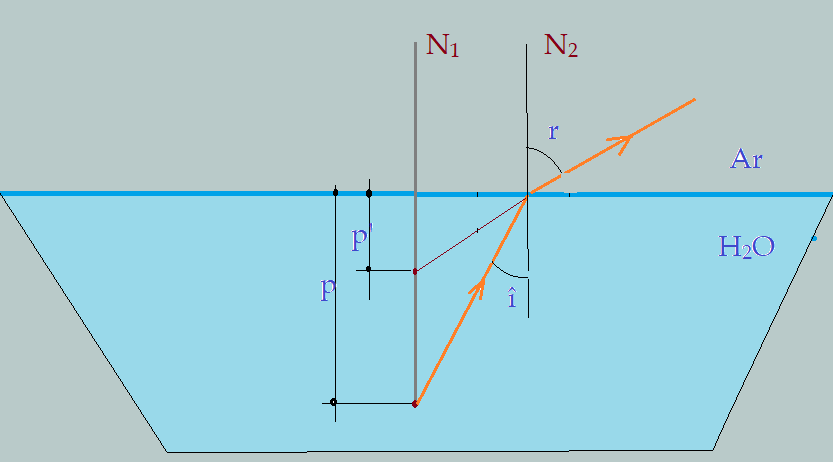
Esse fenômeno acontece com todos os dioptros. Vamos estabelecer uma forma de calcular essa profundidade aparente.

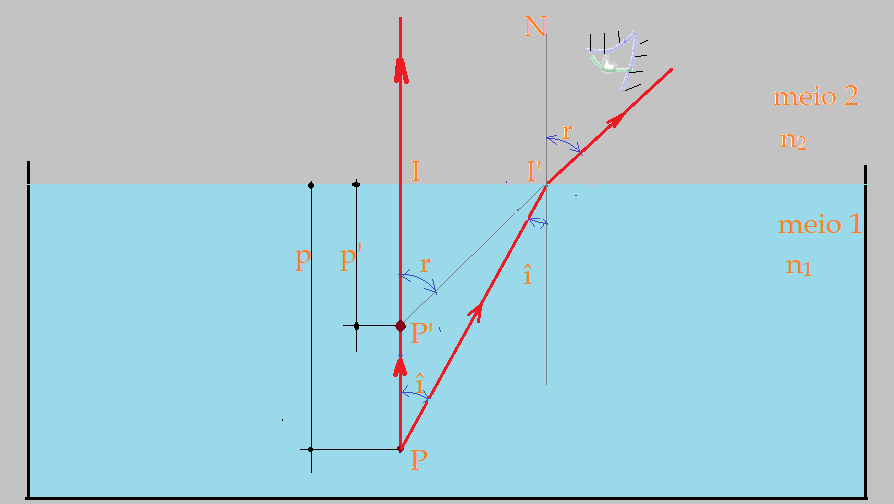
Observando a figura, vemos que existem dois triângulos retângulos, que tem como um de seus lados a profundidade real e o outro a profundidade aparente da fonte de luz, que pode ser qualquer objeto. Vamos representar por $\color{Maroon}{x}$ o segmento de reta $\color{Maroon}{\overline{II’}}$. Os vértices dos ângulos $\hat{P}$ e $\hat{P’}$, são respectivamente iguais aos ângulos $\hat{i}$ e $\hat{r}$ do raio oblíquo que emerge do meio 1, para o meio 2 com desvio angular. Podemos estabelecer as relações:

$$\color{Navy}{tg(i) = \left(\frac{x}{p}\right)}$$

$tg(r) = \left(\frac{x}{p’}\right)$

Para um observador suficientemente próximo da vertical, torna-se válida a aproximação:

$tg (i)\approx sen (i)\approx (i)$

$tg (r)\approx sen (r)\approx (r)$

Isso nos permite escrever a seguinte relação:

$\left[\frac{tg(i)}{tg(r)}\right] = \left[\frac{sen(i)}{sen (r)}\right] = \left(\frac{n_{2}}{n_{1}}\right)$$\Rightarrow$$1$

Da expressão das tangentes nos triângulos tiramos que:

$\left[\frac{tg(i)}{tg(r)}\right] = \left(\frac{\frac{x}{p}}{\frac{x}{p’}}\right)$

$\left[\frac{tg(i)}{tg(r)}\right] = \left(\frac{x}{p}\times\frac{p’}{x}\right)$

Cancelando o fator comum $\color{Maroon}{x}$ entre o numerador e denominador, substituindo a razão entre as tangentes por:

$\left(\frac{n_{2}}{n_{1}}\right)$$\Leftrightarrow$ $\left(\frac{n_{2}}{n_{1}}\right) = \left(\frac{p’}{p}\right)$

Teremos a expressão final:

$\left(\frac{n_{2}}{p’}\right) = \left(\frac{n_{1}}{p}\right)$

Essa expressão podemos aplicar para qualquer situação similar, pois relaciona apenas os índices de refração dos meios com as posições real e aparente do objeto. Se o observador estiver no meio mais refringente, a profundidade aparente será maior que a real.

Elevação aparente das estrelas

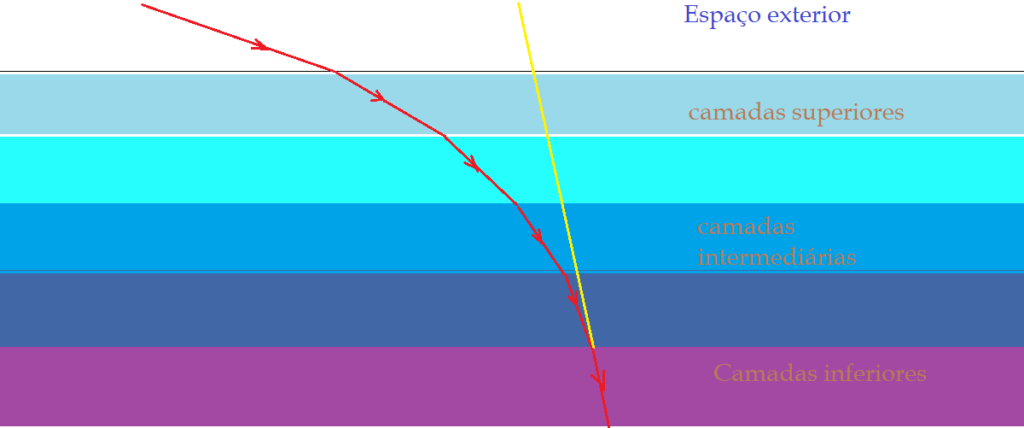
As várias camadas atmosféricas refratando a luz e ela faz uma curva.

Embora o coeficiente de refração do ar seja bastante próximo da unidade, seu valor cresce na medida que as camadas de ar se tornam mais densas, quando nos aproximamos da superfície do globo. Isso resulta num encurvamento dos raios luminosos incidentes, especialmente nas posições próximas do horizonte. Por exemplo a luz do sol, torna-se visível antes que o mesmo chegue a uma posição acima da linha horizontal, por conta desse fenômeno. Por isso a denominação Elevação aparente das estrelas.

Lâmina de faces paralelas

Uma lâmina de faces paralelas é constituída de dois dioptros paralelos. Geralmente é formada por duas superfícies planas que separam três meios, onde o primeiro e o terceiro são habitualmente iguais. Vamos imaginar uma lâmina de vidro, imersa no ar, como mostra a figura.

Os índices de refração dos meios 1 e 3 são geralmente iguais, isso faz com que o raio emergente seja paralelo à direção do raio incidente. Isso resulta num desvio linear lateral $\color{Maroon}{d_{l}}$.

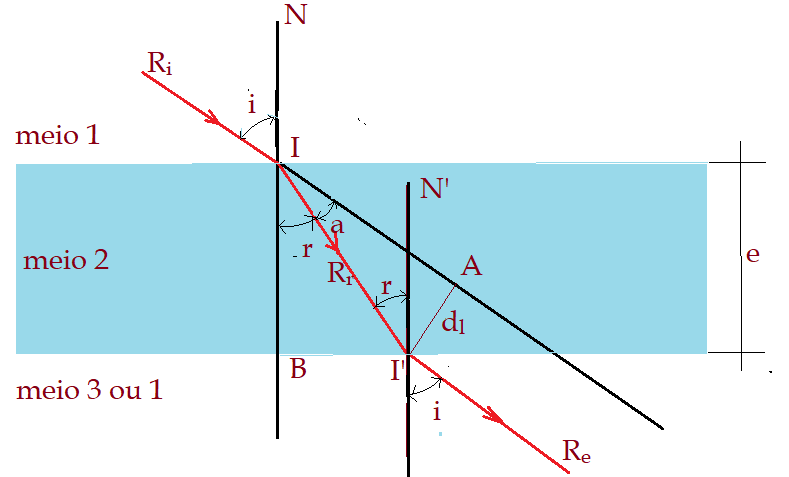
Na figura podemos identificar dois triângulos retângulos, que têm em comum a hipotenusa $\overline{II’}$. São os triângulos $\color{Maroon}{\Delta{IBI’I}}$ e $\color{Maroon}{\Delta{II’AI}}$. Os ângulos adjacentes $\color{Maroon}{î}$ e $\color{Maroon}{â}$, permitem escrever as expressões.

$cos (r) = \left(\frac{\overline{IB}}{\overline{II’}}\right) = \left(\frac{e}{\overline{II’}}\right)$

$sen (a) = \left(\frac{\overline{I’A}}{\overline{II’}}\right) = \left(\frac{
d_{l}}{\overline{II’}}\right)$

Dividindo estas equações membro à membro fica:

$\left[\frac{cos (r)}{seno (a)}\right] = \left[\frac{\left(\frac{e}{\overline{II’}}\right)}{\left(\frac{d_{l}}{\overline{II’}}\right)}\right]$

Cancelando os fatores comuns a expressão se reduz a:

$\left[\frac{cos (r)}{seno (a)}\right] = \left(\frac{e}{d_{l}}\right)$

Rescreveremos esta expressão dessa forma:

$d_{l} = \left[\frac{{e}\cdot{sen(a)}}{cos(r)}\right]$

Observando a figura, vemos que $\color{Maroon}{a = (i – r)}$ e podemos substituir na equação:

$d_{l} = \left[\frac{{e}\times{sen(i – r)}}{cos(r)}\right]$

Algumas situações que podem ocorrer com essas lâminas, variando-se os índices de refração.

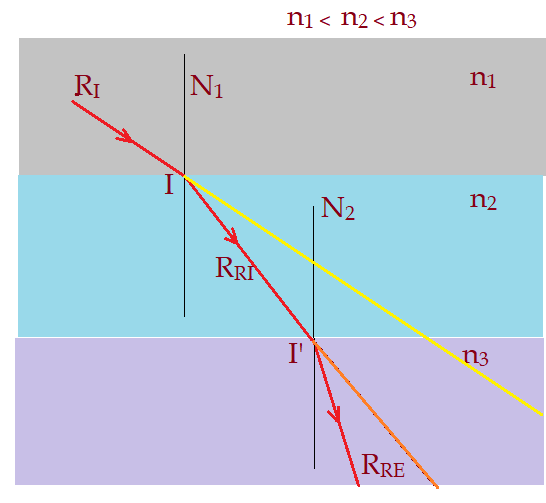
Neste caso os índices de refração estão colocados em ordem crescente. Isso resulta numa espécie de encurvamento da trajetória do raio luminoso.

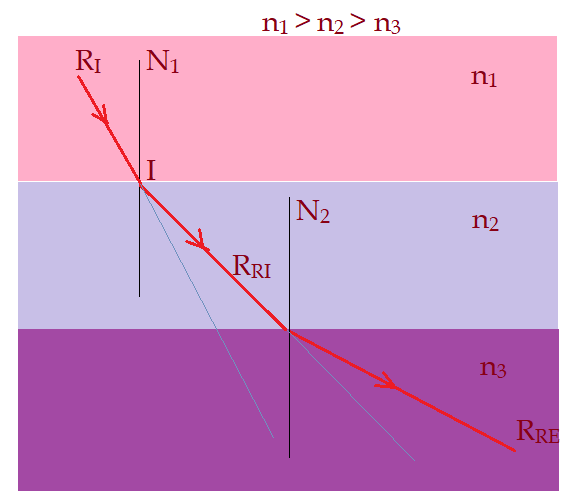
Com os índices de refração em ordem decrescente, o encurvamento é para o outro lado, podendo inclusive ocorrer o fenômeno da reflexão total, quando a incidência ultrapassar o ângulo limite.

Índices de refração em ordem aleatória, podendo haver desvio angular de afastamento ou de aproximação em relação à normal nos pontos de incidência.

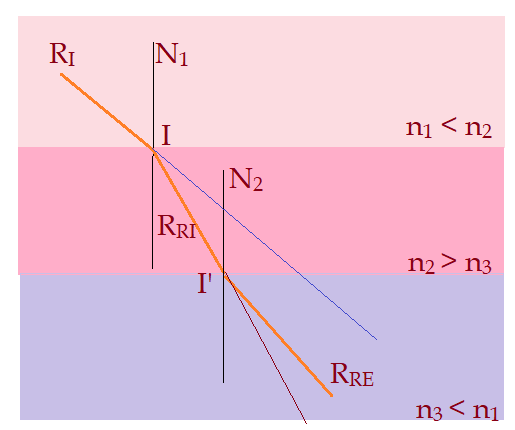
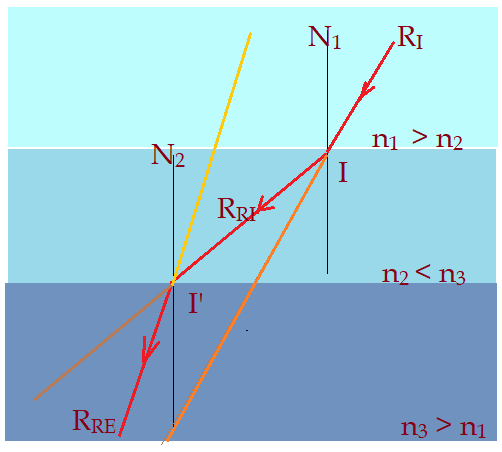
É hora de exercitar.

Um peixe está nadando em água tranquila e cristalina, numa profundidade $\color{Marron}{ p = 2,0\,m}$. Um pescador, armado de um arpão, se prepara para pegar o peixe com uma flechada certeira. Estando próximo da vertical que passa pela posição do peixe, em que profundidade ele deverá apontar o arpão, para ter êxito em sua pescaria? Sabemos que o índice de refração do ar é $\color{Maroon}{n_{ar}\simeq{1}}$ e que o índice de refração da água é $\color{Maroon}{n_{H_{2}O} = \left(\frac{3}{2}\right)}$.

Temos então os dados

$p = 2,0\,m$

$n_{ar}\simeq {1}$

$n_{H_{2}O} = \left(\frac{3}{2}\right)$

Substituindo na fórmula:

$\left(\frac{n_{2}}{p’}\right) = \left(\frac{n_{1}}{p}\right)$

$\left[\frac{\left(\frac{3}{2}\right)}{2,0}\right] = \left(\frac{1}{p’}\right)$

$p’ = \left[\frac{2}{\left(\frac{3}{2}\right)}\right]$$\Leftrightarrow$$\color{Navy}{p’ = \frac{4}{3}\,m}$

Deverá apontar para uma posição situada a $\color{Navy}{\frac{4}{3}m}$ de profundidade.

2. Suponhamos que os olhos do pescador do exemplo anterior estejam a uma altura de $\color{Maroon}{h = 1,60\,m}$ acima da superfície. A que distância o peixe veria os olhos, considerando os demais valores inalterados?

Temos agora o peixe na posição de observador, o que inverte o sentido da trajetória da luz. Substituindo na fórmula teremos:

$\frac{n_{ar}}{1,60} = \frac{n_{H_{2}O}}{h’}$

$\frac{1}{1,60} = \frac{\frac{3}{2}}{h’}$

$h’ = {{1,60}\cdot\frac{3}{2}}$$\Leftrightarrow$$\color{Navy}{h’ = 2,40\,m}$

O peixe verá os olhos do pescador a uma distância de $\color{Navy}{2,40 m}$ da superfície da água.

3) Uma piscina de saltos ornamentais tem profundidade de ${p = 8,0 m}$. Se o índice de refração da água é ${n_{H_{2}O} = {{4}\over{3}}}$, qual é a profundidade aparente dessa piscina?

Dados: ${n_{ar}\simeq {1}}$ $\rightarrow$ ${n_{2}}$

${n_{H_{2}O} = {{4}\over{3}}}$ $\rightarrow$ ${n_{1}}$

${p = 8,0 m}$

Na fórmula ${{n_{2}}\over{p’}} = {{n_{1}}\over{p}}$

${{{1}\over{p’}} = {{{4}\over{3}}\over{8,0}}}$

${{p’}\cdot {{4}\over{3}} = {8,0}}$ $\Leftrightarrow$ ${p’ = {{{3}\over{4}}\cdot{8,0}}}$

${p’ = 6,0 m}$

A piscina tem profundidade aparente de ${6,0 m}$.

4) Uma lâmina de vidro tem espessura de ${15,0 cm}$ e o material tem índice de refração ${n_{2} = \sqrt{2}}$. Ela está imersa no ar com ${n_{1}\simeq{1}}$. Um raio de luz monocromático incide numa das faces formando um ângulo ${i = 60º}$. Determinar o ângulo de refração na primeira face e o desvio linear lateral sofrido por esse raio de luz.

${{sen(i)\cdot{n_{1}}} = {sen(r)\cdot{n_{2}}}}$

Substituindo os valores informados:

${{sen(60º)\cdot{1}} = {sen(r)\cdot{\sqrt{2}}}}$

${{{\sqrt{3}\over{2}}\cdot {1}} = {sen(r)\cdot\sqrt{2}}}$

$sen(r) = \left({{{\sqrt{3}\over{2}}\over \sqrt{2}}}\right) = \left({{\sqrt{3}\cdot\sqrt{2}}\over 2\cdot\sqrt{2}^2}\right)$

${sen(r)} = {\sqrt{6}\over{4}}$$\Leftrightarrow$${sen(r)} = 0,612$

${r}\simeq{37,7º}$

${{d_{l}} = {{e}\cdot{{sen(i – r)}\over{cos(r)}}}}$

${{d_{l}} = {{15,0}\cdot{{sen(60º – 37,7º)}\over{cos(37,7º)}}}}$

${{d_{l}} = {{15,0}\cdot{{sen(22,3º)}\over{cos(37,7º)}}}}$

${{d_{l}} = {{15,0}\cdot{{0,379}\over{0,791}}}}$

${{d_{l}} = {{15,0}\cdot{0,30}}}$

${{d_{l}} = 4,5 cm}$

O raio de luz sofre um desvio de aproximadamente 4,5 cm em relação à direção do raio incidente.

5)Um raio luminoso propaga-se em um tanque de água cristalina. Uma parede de vidro está colocada paralela à uma outra, separadas de uma distância de ${40,0 cm}$. Entre as paredes existe ar atmosférico. Se a luz incide num lado dessas paredes por um ângulo ${i = 30º}$. Se o índice de refração da água é ${n_{H_{2}O} = {{4}\over{3}}}$, qual é o desvio lateral sofrido por esse raio luminoso ao emergir na segunda parede?(Considere desprezível a espessura das camadas de vidro).

Calculamos primeiro o ângulo de refração na face de incidência.

${e = 40,0 cm}$;

${n_{H_{2}O} = {{4}\over{3}}}$$\rightarrow$ ${n_{1}}$

${{n_{ar}}\simeq {1}}$ $\rightarrow$ ${n_{2}}$

${i = 30º}$

${sen(i)\cdot{n_{1}} = sen(r)\cdot{n_{2}}}$

${sen(30º)\cdot{{4}\over{3}} = sen(r)\cdot{1}}$

${sen(r) = {1\over2}\cdot{4\over3}}$

$sen(r) = {4\over6}$$\Leftrightarrow$$sen(r) = {2\over3}$

Isso nos mostra que o ângulo de refração na primeira face é igual $r\simeq{42º}$

${{d_{l}} = {{e}\cdot{{sen(i – r)}\over{cos(r}}}}$

${d_{l}} = {{40,0}\cdot{sen(30º – 42º)}\over{cos(42º)}}$

${{d_{l}} = {40,0}\cdot{{sen(-12º)}\over{cos(42º)}}}$

${{d_{l}} = {40,0}\cdot{{-0,21}\over{0,74}}}$

${{d_{l}}= {{40,0}\cdot{- 0,155}}}$

${{d_{l}}\simeq{- 6,22}cm}$

O deslocamento lateral do raio luminoso será de aproximadamente ${- 6,22 cm}$, no sentido oposto por causa do sinal negativo.

Agora vamos aplicar o que aprendemos. Está na hora de exercitar por conta, resolvendo os exercícios seguintes.

Um helicóptero faz um voo de inspeção sobre as águas transparentes de uma certa região marítima e detecta um submarino a uma profundidade aparente de 450 m no momento em que seus centros estão unidos pela mesma vertical. O índice de refração absoluto da água do mar é 1,5 e o do ar é 1,0. Qual a profundidade real do submarino?
A profundidade de uma piscina vazia é tal que sua parede, revestida com azulejos quadrados de 12 cm de lado, contém 12 azulejos justapostos verticalmente. Um banhista, na borda da piscina cheia de água, cujo $n_{H_{2}O} – 4/3$, olhando quase perpendicularmente, verá a parede da piscina formada por 12 azulejos de medida vertical?
Um raio de luz propagando-se inicialmente no vidro, cujo índice de refração é 2, atinge a superfície que separa o vidro do ar com ângulo de incidência i. Determine o ângulo limite de incidência no dioptro e analise o comportamento do raio luminoso para ângulos de incidência entre ${0 < Li < 90º}$.
Componentes da luz com cores diferentes propagam-se em um meio material refringente com velocidades diferentes, sendo isso um indicativo de que o material apresenta um índice de refração diferente para cada cor. A esse fenômeno dá-se o nome de dispersão cromática da luz. Devido a ele, em geral, feixes de luz com cores diferentes sofrem desvios diferentes ao passarem de um meio refringente para outro. Uma fonte emite luz formada pela composição de duas cores distintas. Para separar as duas cores foi montado o esquema experimental abaixo.

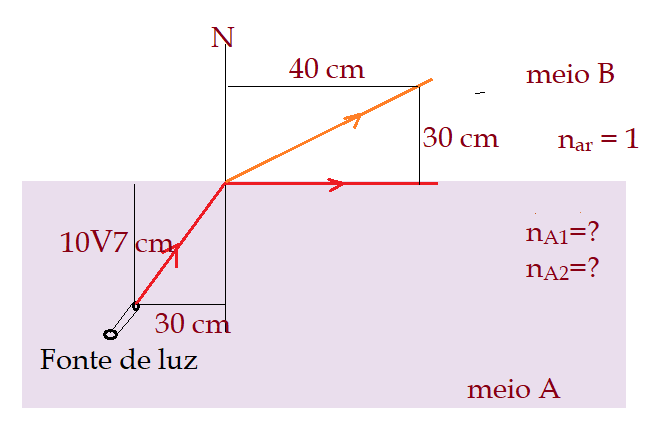
O feixe 1, associado à cor 1, passa do meio A para o meio B, que é ar (n ar =1,0) e segue a trajetória mostrada na figura. O feixe 2, associado à cor 2, sofre reflexão interna total, e sai tangente à superfície que delimita os dois meios. Com isso, consegue-se separar os dois feixes. Quais são os valores dos índices de refração que o meio A deve apresentar para as cores 1 e 2 para que os feixes de cores 1 e 2 se comportem como na figura acima?

5.-(UFRJ) Um cilindro maciço de vidro tem acima de sua base superior uma fonte luminosa que emite um fino feixe de luz, como mostra a figura. Um aluno deseja saber se toda luz que penetra por essa extremidade superior do tubo vai sair na outra extremidade, independentemente da posição da fonte F e, portanto, do ângulo de incidência α. Para tanto, o aluno analisa o raio luminoso
rasante e verifica que o ângulo de refração correspondente a esse raio vale 40°.( Dados: sen 40° = 0,64 e n(ar) = 1 )

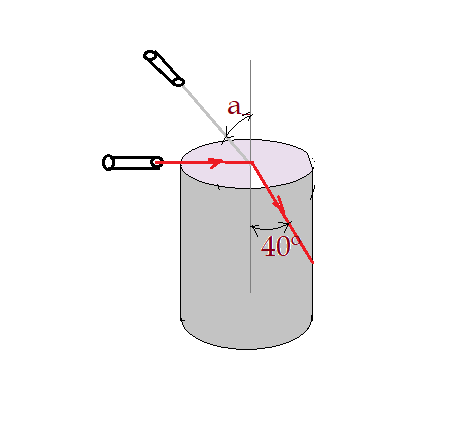
a) Obtenha o índice de refração do material do cilindro. b) Verifique se o raio rasante, após ser refratado e incidir na face lateral do cilindro, sofrerá ou não uma nova refração. Justifique sua resposta.

6. -A luz vermelha se propaga no vidro com velocidade de $2,0. 10^8 m/s$ e no ar com velocidade de $3,0.10^8 m/s$. Um raio de luz vermelha, se propagando no ar, atinge uma das faces de um cubo de vidro com ângulo de incidência igual a 30°. Qual o seno do ângulo de refração?

7. (UFV-MG) Um enfeite de Natal é constituído por cinco pequenas lâmpadas iguais e monocromáticas, ligadas em série através de um fio esticado de comprimento 5L. Uma das pontas do fio está presa no centro de um disco de madeira, de raio R, que flutua na água de uma piscina. A outra ponta do fio está presa no fundo da piscina, juntamente com uma das lâmpadas, conforme representado na figura a seguir:

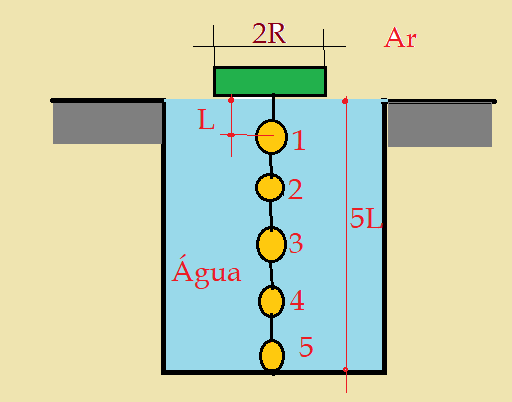
Durante a noite, quando as lâmpadas são acesas, um observador fora da piscina vê o brilho de apenas três das cinco lâmpadas. Sabendo que o índice de refração da água e o do ar são, respectivamente,${n_{H_{2}O}}$ e ${n_{ar}}$, pergunta-se:
a) Qual é o fenômeno que impede a visualização das lâmpadas? b) Qual par de lâmpadas não é visível? c) Qual é a relação entre ${R, L, n_{H_{2}O}, n_{ar}}$ para que duas das lâmpadas não sejam visíveis.

8. Um raio de luz monocromática, propagando-se num meio transparente A, cujo índice de refração é ${n_{A} = 1}$, incide na superfície S de separação com outro meio transparente B, de índice de refração ${n_{B} = 2}$, e se refrata como mostra o esquema a seguir. Qual o valor do ângulo limite quando a luz vai do meio B para o meio A?

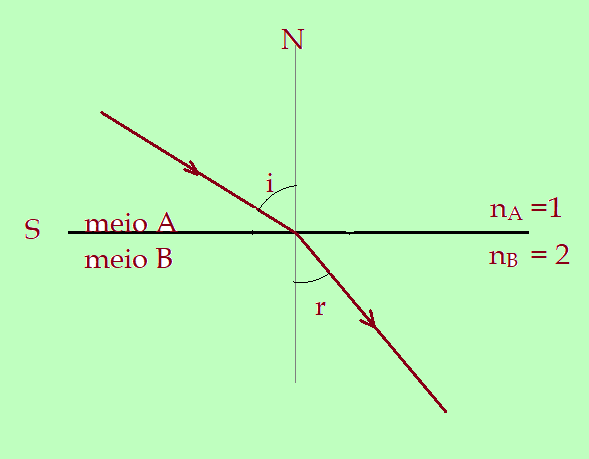
9. Um peixe está parado a 1,2 m de profundidade num lago de águas tranquilas e cristalinas. Para um pescador, que o observa perpendicularmente à superfície da água. Qual a profundidade aparente em que o peixe se encontra? (Dado: ${n_{H_{2}O}} = {{4}\over{3}}$.

10. Considere um peixe a uma profundidade de 1,0m e um observador fora d’água, com os olhos a uma distância de 1,0m da superfície da água, conforme mostra o esquema:

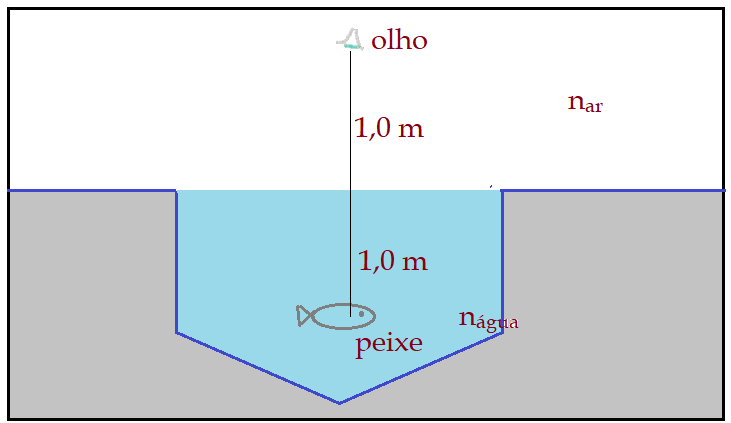
Sendo o índice de refração absoluto da água ${n_{H_{2}O}}= {{4}\over{3}}$, determine:

a) Para o observador, qual a distância aparente entre seu olho e o peixe?

b) Para o peixe, qual a sua distância aparente ao olho do observador?

11. (Unirg) Um policial armado com um fuzil de assalto equipado com uma mira laser aponta para um alvo que se encontra atrás de uma janela com um vidro transparente e espesso, como mostrado na figura abaixo. A espessura D do vidro é igual a 2,00 cm, o índice de refração do vidro é igual a 1,5 e o índice de refração do ar é praticamente igual a 1. As trajetórias da bala e do feixe de luz laser incidem na janela de vidro com um ângulo de θ = 60º em relação à reta normal. O vidro da janela tem uma baixa tenacidade e oferece pouca resistência à passagem da bala, de modo que esta segue com sua trajetória retilínea praticamente inalterada. Ao passo que a luz do laser sofre um desvio x levando o policial a mirar em um ponto diferente do que o cano da arma aponta. Com base nessas informações, o desvio x em relação ao ponto alvo e ao ponto atingido será aproximadamente igual a:

Dados:
sen60º = 0,866 e cos60º = 0,500
sin (a ± b) = sin a cos b ± sin b cos a

12. A espessura de uma lâmina de vidro de faces paralelas é de ${e = {2,0} cm}$. Um raio monocromático de luz incide numa de suas faces com ângulo de${i = 60º}$e se refrata com ângulo de ${r = 45º}$

Considerando ${cos75º = sen15º = {0,25}}$; ${sen60º = {cos30º} = {\sqrt{3}\over{2}} = 0,8}$, ${n_{ar} = 1,0}$ e ${sen45º = cos45º = {\sqrt{2}\over{2}} = {0,7}}$, pede-se:

a) Esboçar o trajeto do raio de luz ao atravessar a lâmina;

b) Determinar o índice de refração do vidro;

c) Determinar o desvio lateral ${d_{l}}$ e o desvio angular $\beta$;

d) Determinar o valor do ângulo de emergência.

13. Determine o desvio aproximado sofrido por um raio de luz que atravessa uma lâmina de faces paralelas com 1,5 cm de espessura. Os ângulos de incidência na passagem da luz do meio externo para a lâmina e da lâmina para o meio externo são, respectivamente, 45° e 30°.

DADOS:
sen 15° = 0,26
sen 45° = 0,71
cos 45° = 0,71
sen 30° = 0,50
cos 30° = 0,87

14. Temos duas lâminas de faces paralelas, sendo a primeira de materia sintético transparente, cujo índice de refração vale ${n_{1} = 1,48}$ e a outra de vidro com índice de refração ${n_{vidro} = 1,4}$. Se elas são sobrepostas de modo a termos os meios em sequência ar, sintético, vidro e ar novamente, um raio luminoso incidindo no primeiro dioptro por um ângulo de ${i = 60º}$ e considerando o ${n_{ar} = 1}$, vamos determina:

a) o ângulo de refração na primeira face;

b) o ângulo de incidência e refração na face intermediária entre sintético e vidro;

c) o ângulo de incidência e refração na face vidro/ar;

d) o desvio linear lateral sofrido pelo raio luminoso ao atravessar esse dispositivo.

Havendo dúvidas, não se acanhe. Peça ajuda por meio de um dos canais listados abaixo.

Respostas:

01) submarino está a 675 m de profundidade.

02)o nadador verá 12 azulejos com altura aparente de 10,33 cm.

03)a)o ângulo limite é igual a 30º; b) para $0 < î < 30º$$Rightarrow$$ 30< \hat{r} < 90º$; c)para $30 < î < 90º$$Rightarrow$ ocorre reflexão total.

04)Os índices de refração devem ser $n_{A}_{1} = sqrt{7}\over4$ e $n_{A}_{2} = \sqrt{7}\over 3$.

05)$n_{2}\simeq1,56$. Não ocorre nova refração na parede lateral do cilindro, pois o ângulo de incidência é maior que o ângulo limite.

06)$\hat{r}\simeq 48,6º$

07) a)a reflexão total impede a visualização de duas lâmpadas; b)as lâmpadas invisíveis são a (1) e (2); c) a relação entre as grandezas é ${{R\over{2L}}= {1\over n_{H_{2}O}$.

08) $ L = 30º$

09) p’ = 0,9 m.

10)a)distância aparente entre olho do pescador e o peixe é 1,75 m: b) distância aparente entre o olho do peixe e o pescador é 2,33 m.

11) o feixe de laser é desviado em 0,35 cm.

12)a)$n_{2} = 1,14$; b) $d_{l} = 0,6 cm e não há desvio angular $\beta = 0$

13)$n_{2} = 1,402$;$d_{l} = 0,45$.

14)a)$\hat{r}_{1} = 35,8º$; b)$î_{2} =35,8º$; c)$\hat{r}_{2} = 38,3º$; d)$î_{3} = 60,2º$.

Curitiba, 20 de outubro de 2019. (atualizado 02/12/2019)

Décio Adams

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams