Massa específica.

Por incrível que pareça, já Arquimedes, há mais de 200 anos antes de Cristo, percebeu que os diferentes materiais, apresentam massas diferentes, em volumes iguais. Tanto isso é verdade que o conhecido Princípio de Arquimedes, sobre empuxo, tem a densidade como base. Densidade e massa específica não são sinônimos, porém são intimamente ligadas. Muitos autores denominam a massa específica de densidade absoluta. Foi essa a forma encontrada pelo cientista grego para provar que a coroa do rei não era de ouro maciço e sim feita de outro metal, recoberto de ouro. Vamos falar nos detalhes depois.

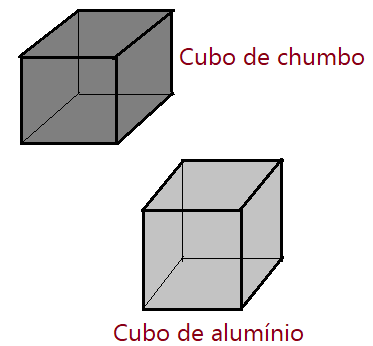
Se colocarmos dois cubos de mesmo volume, sendo um feito de chumbo e o outro de alumínio, sobre uma balança, verificaremos uma significativa diferença em sua massa. Assim fica evidente que existe diferença entre a natureza dos dois metais.

• “A massa específica de uma substância é obtida pela divisão da massa de um corpo dela constituído, pelo seu respectivo volume”.

Usamos para representar a grandeza, a letra grega “mi”, a massa por $m $ e o volume por $V$. Teremos então:

• $\bbox[5px,border:2px solid Olive]{\color{Navy}{\mu = {m\over V}}}$

Sendo as unidades de massa no SI o $\color{Navy}{m = quilograma (kg)}$ e volume o metro cúbico $\color{Navy}{V = m^3}$, teremos como unidade de massa específica o:

• $\bbox[4px,border:2px solid Olive]{\color{Navy}{\mu = kg/m^3}}$

A unidade de massa específica é pois o quociente da unidade de massa, pela unidade de volume no sistema de unidades que se está usando.

Vamos citar algumas outras unidades que poderão aparecer, se o sistema de unidades usado não for o SI. Veja os exemplos:

• $\color{Navy}{g/cm^3}$; $\color{Navy}{utm/m^3}$; $\color{Navy}{g/l}$; $\color{Navy}{ton/m^3}$

É possível estabelecer relações entre as unidades nos diferentes sistemas de unidades. Para isso precisamos da relação entre as unidades de massa e de volume. Vejamos:

• $\color{Navy}{1 kg = 10^3 g}$
• $\color{Navy}{1m^3 = 10^6 cm^3}$

Substituindo as unidades na razão da massa específica, teremos:

• $\color{Navy}{1\,kg/m^3= \frac{10^3 g}{10^6\,cm^3}}$
• $\color{Navy}{1\,kg/m^3 = 10^{-3}\,g/cm^3}$

Se fizermos a transformação inversa, iremos ter:

• $\color{Navy}{1\,g/cm^3 = 10^3\,kg/m^3}$

Procedendo de modo análogo iremos ter:

• $\color{Navy}{1\,kg/m^3= 1,0\,g/l}$
• $\color{Navy}{1\,utm/m^3= 9,8\,kg/m^3}$
• $\color{Navy}{1\,kg/m^3 = \frac{1}{9,8}utm/m^3}$

Algum exercício vai bem!

01. Determine a massa de um paralelepípedo de chumbo, medindo $\color{Sepia}{c = 20\,cm}$, $\color{Sepia}{l = 12\,cm}$ e $\color{Sepia}{h = 10\,cm}$, sabendo que a massa específica do chumbo $\color{Sepia}{\mu_{Pb}= 11, 34\,g/cm^{3}}$.

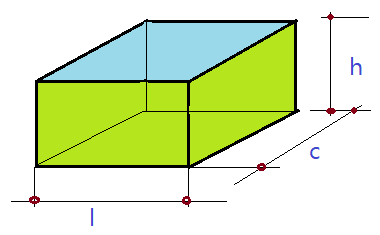
Calcularemos primeiro o volume do sólido.

$$\color{Maroon}{V = c\times l\times h}$$

$V = 20,0\times 12\times 10 = 2400,0\,cm^{3}$

$\mu_{Pb} = \frac{m}{V}$$\Leftrightarrow$$ m = \mu_{Pb}\times V$

$m = 11,34\times 2400,0 = 27216,0\,g$

O paralelepípedo tem massa igual a:

$$\color{Navy}{m = 27216,0\,g}$$

02. Determine a aresta de um cubo de ferro, cuja massa é $\color{Sepia}{m = 62,96\times 10^{3}\,kg}$. Sabendo que a massa específica do ferro é $\color{Sepia}{\mu_{Fe}=7,87\times 10^{3}}$.

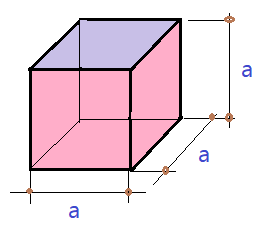
Começaremos pela determinação do volume, a partir da definição de massa específica.

$$\color{Maroon}{\mu = \frac{m}{V}}$$

$V= \frac{m}{\mu_{Fe}}$$\Leftrightarrow$$V = \frac{62,96\times 10^{3}}{7,87\times 10^{3}}$

$V = 8,0\,m^{3}$

O volume de um cubo é a aresta elevada ao cubo. Logo:

$$\color{Maroon}{V= a^{3}}$$

$\sqrt{3}{a^{3}} = \sqrt[3]{8}$$\Leftrightarrow$$a = 2,0\,m$

O cubo tem aresta de:

$$\color{Navy}{a = 2,0\,m}$$

03. Uma viga de concreto mede $\color{Sepia}{3,0\,m}$ de comprimento, tem $\color{Sepia}{0,50\,m}$ de altura e $\color{Sepia}{0,25\,m}$ de largura. Se sua massa é de $\color{Sepia}{m=900\,kg}$, determine a massa específica do material que constitui a viga.

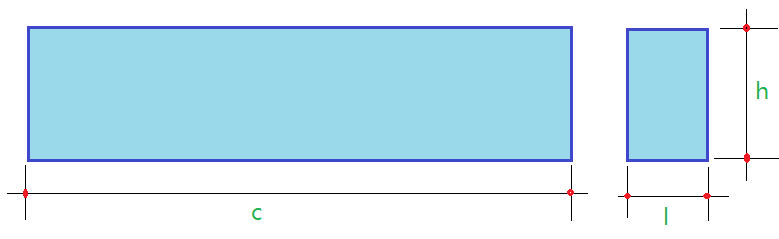
Vejamos o volume da viga, que tem a forma de um paralelepípedo.

$$\color{Maroon}{V = c\times l\times h}$$

$V = 3,0\times 0,50\times 0,25 = 0,375\, m^{3}$

Aplicando a definição de $\mu$, temos:

$$\color{Maroon}{\mu_{con}= \frac{m}{V}}$$

$\mu_{con} = \frac{900,0}{0,375} = 2400,0\,kg/m^{3}$

O concreto dessa viga tem massa específica de:

$$\color{Navy}{\mu_{con}= 2400,0\,kg/m^{3}}$$

04. Um tanque feito de alumínio, mede externamente $\color{Sepia}{c= 1,2\,m}$, $\color{Sepia}{l = 0,80\,m}$ e $\color{Sepia}{h=0,60\,m}$, tendo suas paredes de $\color{Sepia}{e = 6,0\,mm}$ de espessura. A massa específica do alumínio é $\color{Sepia}{\mu_{Al}= 2,7\,g/cm^{3}}$. O tanque contém água até a altura de $\color{Sepia}{h_{H_{2}O}= 35\,cm}$ e $\color{Sepia}{h_{ól}= 20\,cm}$. Sabemos que a água tem massa específica de $\color{Sépia}{\mu_{H_{2}O}=1,0 g/cm^{3}}$ e o óleo $\color{Sepia}{\mu_{ól}=0,78\,g/cm^{3}}$. Determine a massa específica média do tanque com os líquidos.

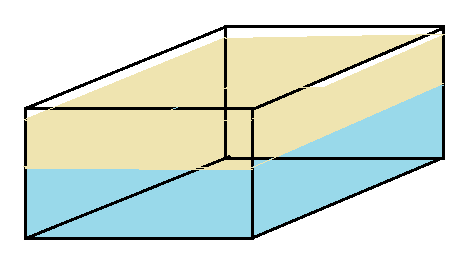
Temos três tipos de materiais. O Alumínio que contém os líquidos, a água e o óleo. É pois necessário determinar os volumes e massas de cada um, somar e por fim obter a massa específica média do conjunto. Vamos resolver tudo isso no SI.

Tanque. São seis faces, congruentes duas a duas. Todas as faces tem a mesma espessura.

Fundo e tampa ou face superior.

$V_{1}= 1,2\times 0,80\times 6,0\times 10^{-3} = 5,76\times 10^{-3}\,m^{3}$

Faces laterais (comprimento)

$V_{2}= 1,20\times 0,60\times 6,0\times 10^{-3}= 4,32\times 10^{-3}\,m^{3}$

Extremidades.

$V_{3}= 0,80\times 0,60\times 6,0\times 10^{-3} = 2,88\times 10^{-3}\,m^{3}$

O volume de alumínio do tanque é então:

$V = 2\times {(V_{1} + V_{2} +V_{3})} = 2\times{[(5,76 + 4,32 + 2,88)\times 10^{-3}]} = 0,02592\,m^{3}$

A massa de alumínio que forma o tanque será então:

$m = \mu_{Al}\times V$$\Leftrightarrow$$m=2,7\times 10^{3}\times 2,592\times 10^{-2}$

$m_{Al} = 69,984\,kg$$\Rightarrow$ massa de alumínio.

Volume de água:

$V_{H_{2}O}= 1,188\times 0,788\times 0,35 = 0,3276\,m^{3}$

$m_{H_{2}O} = 0,3276\times 10^{3} = 3,276\times 10^{2}\,kg$$\Rightarrow$ massa de água.

Volume do óleo.

$V_{ól}= 1,188\times 0,788\times 0,20 = 0,1872\,m^{3}$

$m_{ól} = 0,1872\times 780 = 143,04\,kg$$\Rightarrow$ massa do óleo.

Massa do conjunto.

$m = m_{Al} + m_{H_{2}O} + m_{ól}$$\Leftrightarrow$$m= 67,392 + 327,6 + 143,04 = 540,624\,kg$

Volume externo do tanque:

$V= 1,20\times 0,80\times 0,60 = 0,576\,m^{3}$

$\mu_{ap}= \frac{m}{V}$$\Leftrightarrow$$\mu_{ap}= \frac{540,624}{0,576}= 938,583\,kg/m^{3}$

A massa específica aparente ou média do conjunto é então de:

$$\color{Navy}{\mu_{ap}=938,583\,kg/m^{3}}$$

Em números redondos iríamos considerar.

$$\color{Navy}{\mu_{ap}=939,0\,kg/m^{3}}$$

Tabela de algumas massas específicas

Substância	Unidade($kg/m^{3}$$	Observações
Meio interestelar	$10^{-25} – 10^{-15}$	$90\% H; 10\%He$ variável
Atmosfera terra	$1,2$	Ao nível do mar
Ar(padrão)	$1,2$	a 0ºC e 1 atm
Cortiça	$240 – 260$
Aerogel	$1 – 2 $
Água	$1000$	nas CNTP
Água do mar	$1030$
Gelo	$940$
Plástico	$850 – 1400$	Polipropileno, PET/PVC
Terra	$5520$	Massa específica média.
Cobre	$8920 – 8960$	Temperatura ambiente
Chumbo	$11340$
Tungstênio	$19250$
Ouro	$19330$	24 k (Puro)
Ouro puro fundido	$19250$
Núcleo da Terra	$\simeq 13000$
Urânio	$18950$
Irídio	$22650$
Ósmio	$22610$	Na temperatura ambiente
Núcleo do Sol	$160000$
Núcleo atômico	$\simeq 3.10^{17}$
Estrela de Nêutrons	$8,4.10^{16}-1.10^{18}$
Gasolina	$680$
Álcool etílico	$789$
Mercúrio	$13400$
Glicerina	$1260$
Alumínio	$2700$
Platina	$21400$
Óleo SAE 30	$912$
Prata	$10500$
Ferro	$7870$
Níquel	$8910$
Cromo	$7100$

Densidade.

Disse acima que densidade e massa específica são “parentes”. Há quem afirme que são sinônimos. A diferença entre as duas coisas é:

• Densidade$\rightarrow$ é um número, sem unidade. Tem valor idêntico em qualquer sistema de unidades utilizado.
• Massa específica$\rightarrow$ tem valor diferente em cada sistema de unidades. Seu valor é diferente em cada sistema de unidades.  
• Obs.: Iremos denominar a massa específica de densidade absoluta, como boa parte dos autores faz.

A determinação da densidade de uma substância é feita dividindo-se a massa específica dessa substância, à determinada temperatura, pela massa específica da água, à $4^0C$. Isso por ser essa a temperatura em que a água tem o menor volume. A unidade padrão de massa $\color{Maroon}{1g}$ é definida como a massa de $\color{Maroon}{1\,cm^3}$ de água na temperatura de $\color{Maroon}{\theta\simeq 4^0C}$.

• $$\color{Navy}{\delta = \frac{\mu_{S}}{ \mu_{H_{2}0}}}$$

Alguns exemplos.

• A massa específica da água no SI é:
  • $\color{Navy}{\mu_{H_{2}O} = 10^3 kg/m^3}$
• No CGS teremos:
  • $\color{Navy}{\mu_{H_{2}O} = 1 g/cm^3}$
• No MKgfS, será:
  • $\color{Navy}{\mu_{H_{2}O} = {9,8\times 10^3}utm/m^3}$
• $\color{Navy}{\mu_{H_{2}O} = 10^3\,g/l = 1,0\,kg/l}$

O mercúrio tem massa específica:

• $\color{Navy}{\mu_{Hg} =13,6\,g/cm^3 = 13,6\times 10^3\,kg/m^3}$

Vamos determinar a densidade do mercúrio em relação à água, tomada geralmente como referência.

• $\color{Navy}{\delta_{Hg} = {{\mu_{Hg}}\over{\mu_{H_{2}O}}}}$
• $\color{Navy}{\delta_{Hg} = {{13,6g/cm^3}\over {1g/cm^3}} = 13,6}$
• $\color{Navy}{\delta_{Hg} = {13,6\times 10^3{kg/m^3}}{10^3{kg/m^3}}= 13,6}$

Note que o valor da densidade não depende do sistema de unidades. Ela representa quantas vezes uma unidade de volume de mercúrio, contém a massa de igual volume de água à temperatura de $\color{Maroon}{\theta=4^0C}$$.

Densidade relativa entre substâncias

Assim como podemos determinar a densidade de uma substância qualquer em relação à água, podemos determinar a densidade de uma substância em relação a outra, nas mesmas condições de temperatura.

Sejam as substâncias A e B. A massa específica de A será $\color{Sepia}{\mu_{A}}$ e de B será $\color{Sepia}{\mu_{B}}$. Se quisermos determinar a densidade de A em relação a B, faremos:

$$\color{Brown}{\delta_{AB} = \frac{\mu_{A}}{\mu_{B}}}$$

De B em relação a A, basta inverter as posições na divisão.

$$\color{Sepia}{\delta_{BA} =\frac{\mu_{B}}{\mu_{A}}}$$

01. Vamos determinar a densidade do chumbo em relação à prata, depois da prata em relação ao chumbo. Sendo $\color{Sepia^{\mu_{Pb}=11,34\times 10^{3}\,kg/m^{3}}$ e $\color{Sepia}{\mu_{Ag} = 10,50\times 10^{3}\,kg/m^{3}}$.

$$\color{Maroon}{\delta _{PbAg} = \frac{\mu_{Pb}}{\mu_{AgPb}}}$$

$\delta_{PbAg} =\frac{11,34\times 10^{3}}{10,50\times 10^{3}} = 1,08$

$$\color{Navy}{\mu_{PbAg} = 1,08}$$

Isso nos indica que volumes iguais de chumbo e prata, a massa do chumbo é 1,08 vezes a massa de prata.

$$\color{Maroon}{\mu_{AgPb}=\frac{\mu_{Ag}}{\mu_{Pb}}}$$

$\mu_{AgPb}=\frac{10,50\times 10^{3}}{11,34\times 10^{3}} = 0,926$

$$\color{Navy}{\mu_{AgPb}= 0,926}$$

Então podemos afirmar que, em volumes iguais de prata e chumbo, a massa de prata é igual a $92,6\%$ da massa do chumbo.

02. Um cálice litúrgico, usado em celebrações religiosas, tem massa $\color{Sepia}{m = 768,9\,g}$. Sua composição é liga de ouro e prata, cujas massas específicas são respectivamente $\color{Sepia}{\mu_{Au}=19,33\,g/cm^{3}}$ e $\color{Sepia}{\mu_{Ag}=10,50\,g/cm^{3}}$. Quer-se saber o volume desses dois metais que foram misturados para obter a matéria prima usada na confecção do cálice. Para isso, encheu-se uma bacia totalmente de água e nela mergulhou suavemente o cálice, para transbordar somente o volume deslocado pelo objeto. A água que transbordou foi colhida e colocada em uma proveta, onde se obteve a indicação de $\color{Sepia}{V = 48\,cm^{3}}$. Determinemos agora quanto desse volume é ouro e quanto é prata.

A água derramada nos informa o volume de metal existente no cálice. De posse do volume e da massa, podemos calcular a densidade média do objeto.

$$\color{Maroon}{\mu = \frac{m}{V}}$$

$\mu_{cal}= \frac{768,9}{48}= 16,019\,g/cm^{3}$$|Rightarrow$ massa específica da liga de que foi feito o cálice.

Temos então o volume total e a massa específica da liga.

$V = V_{Au} + V_{Ag}$$\Leftrightarrow$$ 48 = V_{Au} + V_{Ag}$ (I)

$m = \mu_{Au}\times V_{Au} + \mu_{Ag}\times V_{Ag}$$\Leftrightarrow$$768,9 = 19,33\times V_{Au} + 10,50\times V_{Ag}$ (II)

Temos duas expressões para os volumes de ouro e prata. Isolando uma das variáveis na primeira e substituindo na segunda, chegaremos ao resultado.

$V_{Au} = 48 – V_{Ag}$

$768,9 = 19,33\times({48 – V_{Ag}}) + 10,5\times _{Ag}$$\Leftrightarrow$$768,9 = 927,84 – 19,33\times V_{Ag} + 10,5\times V_{Ag}$$768,9 – 927,84 = 10,5\times V_{Ag} – 19,33\times V_{Ag}$$\Leftrightarrow$$- 158,94 = – 8,83\times V_{Ag}$

$V_{Ag} = \frac{-158,94}{- 8,83}$$\Leftrightarrow$$V_{Ag} = 18\,cm^{3}$

$V_{Au} = 48 – V_{Ag}$$\Leftrightarrow$$V_{Au}= 48 – 18 = 30\,cm^{3}$

O cálice é confecionado com a liga de $18cm^{3}$ de prata e $30cm^{3}$ de ouro, o que corresponde a um percentual de $62,5\%$de outo e $37,5\%$ de prata.

Podemos demonstrar esses percentuais por regra de três.

$ 100\% = 48\,cm^{3}$

$ x = 30\,cm^{3}$$\Leftrightarrow$$ x = \frac{100 x 30}{48} = 62,5\%$

$ x = 18\,cm^{3}$$\Leftrightarrow$$ x = \frac{100\times 18}{48}= 37,5\%$

Peso específico

• O peso específico de uma substância representa o peso existente em uma unidade de volume da substância. 
• $$\color{Navy}{\rho = frac{P}{V}}$$

Como o peso é obtido multiplicando a massa do corpo pela aceleração da gravidade, podemos também determinar o peso específico multiplicando a massa específica pela aceleração da gravidade.

• $\rho = \frac{m\times g}{V}= \frac{m}{V}\times g$

• $\color{Navy}{\rho = {\mu\times g}}$

Vamos calcular o peso específico do ouro. Temos que:

• $\color{Navy}{\mu_{A_u}= 19,3\times 10^3\,kg/m^3}$
• $\color{Navy}{\rho_{A_u} = \mu_{A_u}\times g = {19,3\times 10^3}\times {9,8}}$
• $\color{Navy}{\rho_{A_u} = {19,3\times 10^3}\times {9,8} = 188,16\times 10^3\,N/m^3 =18,82\times 10^4\,N/m^3}$

Vamos exercitar um pouco o que vimos hoje. Outro dia caminhamos mais um pouco.

•  Um bloco de alumínio tem aresta de $\color{Sepia}{0,3\,m}$. A massa específica do alumínio é $\color{Sepia}{2,7.10^3\,kg/m^3}$. Qual é a massa desse bloco?

Se a aresta é $a = 0,3\,m$, trata-s de um cubo e o volume é essa aresta elevada à terceira potência.

$\color{Maroon}{V = a^{3}}$

$V = 0,3^{3} = 0,027\,m^{3}$

$$\color{Maroon}{\mu = \frac{m}{V}}$$

$m = \mu\times V$$\Leftrightarrow$$m = 2,7\times 10^{3}\times 27\times 10^{-3}$

$$\color{Navy}{m = 72,9\,g}$$

•  Determine o peso específico no SI para o chumbo, cuja massa específica é $\color{Sepia}{11,34.10^3\,kg/m^3}$. Considere a aceleração da gravidade igual a $ \color{Sepia}{10 m/s^2}$.

$$\color{Maroon}{\rho = \mu\times g}$$

$\rho = 11,34\times 10^{3}\times 10$$\Leftrightarrow$$\rho = 11,34\times 10^{4}$

$$\color{Navy}{\rho = 11,34\times 10^{4}\,N/m^{3}}$$

•  Que volume tem um trilho de ferro de massa igual a $\color{Sepia}{3365,4\,kg}$? A densidade do ferro em relação à água é $\color{Sepia}{7,9}$.

$$\color{Maroon}{\delta = \frac{\mu_{Fe}}{\mu_{H_{2}O}}$$

$\mu_{Fe} = \delta_{Fe}\times \mu_{H_{2}O}$$\Leftrightarrow$$\mu_{Fe}= 7,9\times 10^{3}\,kg/m^{3}$

$$\color{Brown}{\mu = \frac{m}{V}}$$

$V = \frac{m}{\mu}$$\Leftrightarrow$$V = \frac{3365,4}{7,9\times 10^{3}}$

$$\color{Navy}{V = 0,426\,m^{3}}$$

Hora de trabalhar um pouco sozinho, não acha!

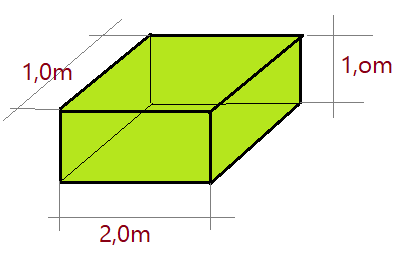
01. Supondo que a figura representa um bloco homogêneo de ferro. Determine a massa específica, sabendo que sua massa é igual a $\color{Sepia}{m = 15.200,0\,kg}$.

02. A massa específica da gasolina é $\color{Sepia}{\mu=0,66\,g/cm^{3}}$. Em um tanque com capacidade para $\color{Sepia}{V= 10000\,l$, qual é a massa de gasolina correspondente?

03. Calcular o peso específico de um cano metálico de $\color{Sepia}{m= 6,0\,kg}$ e cujo volume tubular é de $\color{Sepia}{V = 4\times 10^{-4}\m^{3}}$.

04. O heptano e o octano são duas substâncias que entram na composição da gasolina. Suas massas específicas valem, respectivamente $\color{Sepia}{\mu_{H}= 0,68\,g/cm^{3}}$ e $\color{Sepia}{\mu_{Oc}=0,70\,g/cm^{3}}$. Desejamos saber a densidade da gasolina obtida, misturando-se heptano na proporção $\color{Sepia}{V=65\,cm^{3}}$ e octano $\color{Sepia}{V = 35\,cm^{3}}$.

05. Suponhamos que você possua $\color{Sepia}{m=60\,g}$ de massa de uma substância cujo volume é de $\color{Sepia}{V=5\,cm^{3}}$. Calcule a densidade absoluta (massa específica) dessa substância nas unidades $\color{Sepia}{g/cm^{3}}$e $\color{Sepia}{kg/m^{3}}$ e marque a opção correta.

( )a) $12\,g/cm^{3} e 12\times 10^{-4}\,kg/m^{3}$;
( )b) $1,2\,g/cm^{3} e 12\times 10^{4}\,kg/m^{3}$;
( )c) $14\,g/cm^{3} e 12\times 10^{4}\,kg/m^{3}$;
( )d) $12\,g/cm^{3} e 12\times 10\,kg/m^{3}$;
( )e) $8\,g/cm^{3} e 12\times 10^{-4}\,kg/m^{3}$.

06. Hidrostática é o ramo da Física que estuda as propriedades relacionadas aos líquidos ou gases sob a ação da gravidade em equilíbrio estático. De acordo com o estudo da hidrostática, marque a alternativa que melhor define massa específica.

( )a) massa específica de uma substância é o quociente entre o volume ocupado por uma substância e a massa de uma porção oca de uma substância;

( )b) massa específica é a razão entre a densidade absoluta de uma substância pela densidade de outra substância tomada como padrão;

( )c) massa específica, também chamada de densidade absoluta, de uma substância é a razão entre a massa de uma porção compacta e homogênea dessa substância e o volume ocupado por ela;

( )d) massa específica é a quantidade de matéria que cabe em um volume de um litro dessa substância;

( )e) massa específica é a própria densidade relativa da substância.

07. Calcule a densidade da mistura de dois líquidos homogêneos de massas iguais e massas específicas respectivas de $\color{Sepia}{\mu_{1}=4,2 g/cm^{3}}$ e $\color{Sepia}{\mu_{2}=1,4\,g/cm^{3}}$. Marque a opção correta cuja unidade seja dada em $\color{Sepia}{g/cm^{3}}$.

( )a) $\mu = 2,1\,g/cm^{3}}$;
( )b) $\mu = 5,2\,g/cm^{3}}$;
( )c) $\mu = 1,6\,g/cm^{3}}$;
( )d) $\mu = 0,4\,g/cm^{^{3}}$;}
( )e) $\mu = 2,5\,g/cm^{3}}$.

08. Determine a massa, em $\color{Sepia}{kg}$, de um bloco de ferro maciço em forma de cubo cuja aresta mede $\color{Sepia}{a =10\,cm}$. Suponha que a massa específica do ferro seja igual a $|color{Sepia}{\mu_{Fe}=7,8\,g/cm^{3}}$.

( )a) $m = 78\,kg$;
( )b) $m = 0,78\,kg$;
( )c) $m = 0,0078\,kg$
( )d) $m = 8,7\,kg$
( )e) $m = 7,8\,kg$.

Em caso de dúvidas, faça contato por um dos canais abaixo para esclarecimentos.

Curitiba, 07 de maio de 2015 (Revisado e atualizado em 05/08/2016). Republicação em 25/10/2017).

Décio Adams

[email protected]

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@DcioAdams

Telefone: (41) 3019-4760

Celular e WhatsApp: (41) 99805-0732

Tags: #densidade, #estática, #física, #massa específica, #mecânica, #peso específico.