Física – Comportamento térmico dos gases.
O que é um gás?
Rigorosamente falando, gás é uma substância no estado gasoso, que não se liquefaz sob nenhuma pressão. Essa condição se verifica quando está numa temperatura acima da denominada “ponto crítico” ou “temperatura crítica”.
O que é vapor?
Toda substância, ao passar do estado líquido para o gasoso, no processo chamado de vaporização, passa a ser apenas vapor. Ao atingir a “temperatura crítica”, que é diferente para cada substância, ela se transforma em gás. Para algumas substâncias essa temperatura é bastante baixa, bem próximo do zero absoluto, enquanto para outras é muito elevada.
Para citar um exemplo, tomemos a água. Ela se vaporiza por ebulição a temperatura próxima dos $\theta = 100^{0}C$. Só transforma em gás ao ultrapassar a temperatura de $\theta_{cr}={374,15}^{0}C$. Há entre os engenheiros de centrais de geração elétrica e outras aplicações o costume de referir-se à água no estado de gás com a denominação de “vapor super aquecido”. Desconheço a origem desse costume, mas mantendo-nos dentro dos cânones da física, usaremos nesses casos a denominação gás_{H_{2}O}. Nas condições abaixo dessa temperatura teremos apenas vapor de água. Se aplicarmos uma pressão suficientemente elevada sobre qualquer porção de vapor d’água, com temperatura abaixo desse valor crítico ela irá se liquefazer. Se for aquecida irá se vaporizar novamente. Isso nos permite manter água no estado líquido até ao limiar da temperatura crítica, bastando exercer sobre ela a pressão adequada.
Temos mais alguns exemplos:
a) Álcool etílico: $\theta_{C} =243,1^{0}C$;
b) Carbono: $\theta_{C} = 31,04^{0}C$;
c) Hélio: $\theta_{C}= -267,9^{0}$.
Nota: Isso nos mostra que o gás hélio terá uma margem estreitíssima entre o estado de gas e o zero absoluto.
Gás perfeito.
É um conceito idealizado, para o qual se aplicam as leis dos gases que veremos a seguir. Qualquer substância gasosa (vapor ou gás} se aproxima da condição de gás perfeito quanto mais elevada for sua temperatura e mais baixa sua pressão correspondente. Só isso nos mostra que na prática é condição difícil de realizar. São poucas as substâncias que no estado gasoso se aproximam dessa condição.
Variáveis de estado de um gás
São as grandezas que caracterizam a porção de matéria. Nos sólidos vimos que sua forma é constante, seu volume varia pouco com a dilatação, a massa permanece constante. Os líquidos assumem a forma do recipiente em que estão contidos, seu volume varia mais acentuadamente do que nos sólidos e a massa, antes de ocorrer evaporação, permanece constante. Nas substâncias gasosas observamos que a forma, o volume, variam conforme as demais condições. Para completar a sua caracterização usamos a pressão e a temperatura absoluta. Para variar a massa, teremos que retirar uma parte da substância do recipiente ou injetar outra porção. Isso nos mostra que é possível analisar o comportamento de uma massa gasosa por meio das três variáveis ou grandezas: pressão, volume e temperatura absoluta.
Pressão: – devido a grande liberdade de movimentação as moléculas ou partículas no estado gasoso estão em constante movimento de agitação no interior do recipiente. Para fazer uma ideia, imagine um enxame de insetos, retidos dentro de um frasco de vidro transparente. Eles voam aleatoriamente em todas as direções e sentidos, chocam-se com as paredes e entre si. O mesmo acontece com a substância gasosa num recipiente fechado qualquer. A somatória dos impactos contra as paredes se traduz em uma força resultante, que dividida pela área da superfície interna, nos fornece a pressão. Para medir a pressão usa-se um dispositivo denominado manômetro. As unidades são as mesmas já estudadas na ocasião em que vimos a pressão em líquidos. A movimentação contínua, ininterrupta das partículas do gás no interior do recipiente, é consequência da força de repulsão entre elas, que as faz tender a se afastar cada vez mais umas das outras. Quando o estado é sólido, as forças de atração (coesão) são mais intensas que as de repulsão. No estado líquido, as forças de coesão ainda são suficientes para manter a massa de partículas juntas, com exceção de algumas que conseguem romper a ligação e escapar para o ambiente. Esse fenômeno é a evaporação. Ao vaporizar-se as forças de coesão deixam de existir ou se tornam muitíssimo pequenas e assim as partículas se tornam livres para mover-se.
Volume: – o volume é igual ao do recipiente que o contém. Para variações consideráveis de temperatura esse volume irá sofrer ligeiras alterações.
Temperatura absoluta: – é a temperatura medida na escala Kelvin.
Transformações isotérmicas
Uma transformação é isotérmica quando ocorre sem variar a temperatura. No caso dos gases ideais essas transformações obedecem a Lei de Boyle-Mariotte. Foi estabelecida por Robert Boyle, contemporâneo de Edem Mariotte. Parece que trocaram informações e quem apresentou o resultado foi Boyle. Isso ocorreu no século XVII. Esta lei é interpretada matematicamente pela expressão:
$$\color{Blue}{p_{0}\times V_{0} = p\times V}$$
Enunciado: “Nas transformações isotérmicas de uma massa de gás ideal, a pressão e o volume são grandezas inversamente proporcionais.”
Dessa forma, a representação gráfica num plano cartesiano resulta em uma hipérbole. Esse gráfico denominamos “isoterma”. Num mesmo gráfico podemos representar várias transformações do mesmo gás, formando um feixe de isotermas. Quanto mais elevada for a temperatura, mais distantes elas ficam em relação aos eixos. Temos uma função $p = f(V)$
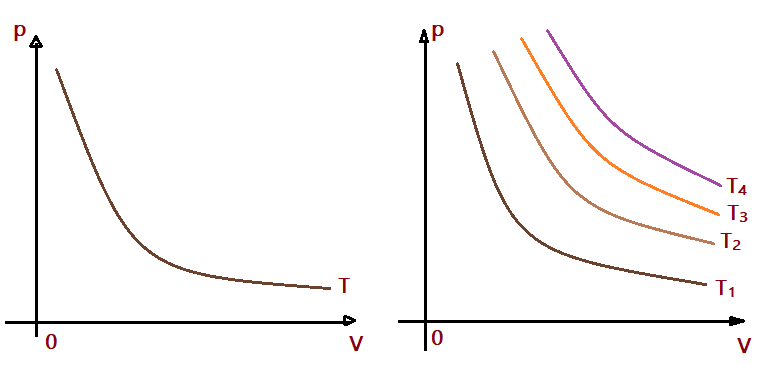
$$\color{Brown}{T_{1} < T_{2} < T_{3} < T_{4}}$$
Transformações isométricas
As transformações que ocorrem mantendo o volume constante, são denominadas isométricas ou isocóricas. Para os gases ideais, elas são estudadas pela Lei de Charles. Foi estudada e apresentada por Jacques Alexandre Cesar Charles (1746/1823). O enunciado diz:
Lei de Charles: “Uma massa de gás ideal mantida a volume constante, tem sua pressão diretamente proporcional à temperatura absoluta”.
$$\color{Blue}{\frac{p_{0}}{T_{0}} = \frac{p}{T}}$$
Sendo diretamente proporcional, a representação gráfica cartesiana $\color{Sepia}{p = f{(T)}}$ da transformação será uma linha reta, que, ficará mais inclinada na medida em que o volume aumenta. Estes gráficos denominamos isômetras ou isócoras.
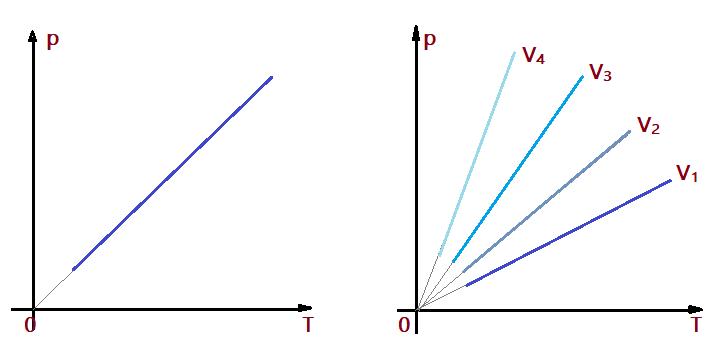
$$\color{Brown}{V_{1} < V_{2} < V_{3} < V_{4}}$$
Transformação isobárica
As transformações que ocorrem mantendo-se a pressão constante, são denominadas isobáricas. Elas são estudadas à luz da Lei de Gay-Lussac. O frances Joseph Louis Gay-Lussac (1778/1850) foi quem publicou o enunciado dessa lei, que diz:
Lei de Gay-Lussac: “Em uma transformação isobárica o volume de uma massa de gás ideal é diretamente proporcional à temperatura absoluta”.
Essas transformações podem ser representadas graficamente na forma $\color{Sepia}{V=f{(T)}}$, formando uma linha reta. Podemos representar várias transformações no mesmo gráfico. Quanto maior a pressão, mais inclinada será a reta do gráfico.
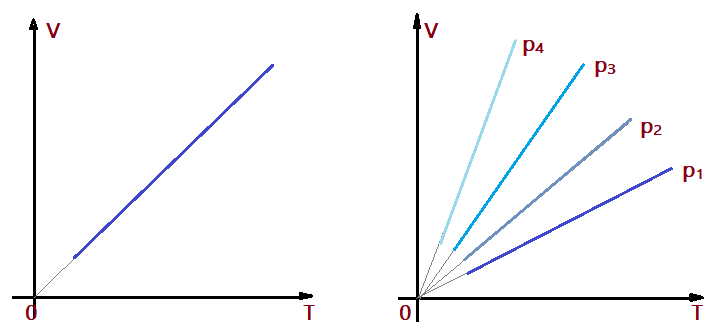
$$\color{Brown}{p_{1} < p_{2} < p_{3} < p_{4}}$$
Lei Geral dos Gases Perfeitos
Juntando as três leis vistas acima, podemos estabelecer uma Lei Geral para os gases perfeitos
“Em uma massa de gás ideal o produto da pressão pelo volume é diretamente proporcional à temperatura absoluta”.
$$\color{Brown}{\frac{p_{0}\times V_{0}}{T_{0}} = \frac{p\times V}{T}}$$
Vemos que existe aí uma relação constante e podemos estabelecer uma relação entre as variáveis aqui usadas, com a massa de gás em questão.
Os fatores $n$ e $R$ têm os significados:
a) $n = \frac{m}{M}$$\rightarrow$ é o número de mols do gás da amostra em estudo. O $m$ representa a massa do gás e $M$ a massa molar.
b) R é denominado “constante universal dos gases perfeitos”, derivada da Constante de Boltzmann. Legada por Stefan Boltzmann. Seu valor é:
$$\color{Brown}{R = 0,082\frac{atm\times L}{mol\times K} = 62,3\frac{mmHg\times L}{mol\times K}= 1,99\frac{cal}{mol\times K} = 8,31\frac{J}{mol\times K}}$$
Mol
É a unidade usada para especificar uma quantidade de matéria microscópica como átomos e moléculas. A origem é a do latim mole, cujo significado é quantidade. Surgiu com Amedeo Avogadro, por volta de 1811. Seu idealizador nasceu em 1776 e faleceu em 1856, aos 80 anos de idade.
O valor do chamado Número de Avogadro, foi determinado pelos estudos de Jean Baptiste Perrin, no século XX. Antes também houve trabalhos realizados nesse sentido por Wilhelm Ostwald em 1896. O valor hoje aceito é:
$$\color{Brown}{N = 6,022\times {10}^{23}}$$
A massa molar ou massa de um mol de uma substância é representada por M. É o valor na unidade $g$ de um mol de entidades (moléculas, átomos, íons, etc) de uma substância. O número de entidades de um mol é o número de Avogadro, especificado acima.
Obs.: A massa molar é igual a massa atômica de um mol da substância ou a soma das massas atômicas de um mol no caso das substâncias compostas.
Voltando à expressão mencionada anteriormente:
$$\color{Blue}{\frac{p\times V}{T} = n\times R}$$
Podemos agora dar o nome a equação. É chamada Equação de Clapeyron e também pode ser escrita na forma:
$$\color{Brown}{p\times V = n\times R\times T}$$,
$$\color{Brown}{p\times V =\frac{m}{M}\times R\times T}$$
Condições normais de temperatura e pressão:
Consideramos como essas condições os valores de:
a) $$\color{Brown}{T_{N}= 273,15 K = 0^{0}C}$$
b) $$\color{Brown}{p_{N} = 1\, atm = 1,01325 bar = 101325 Pa}$$
Nestas condições de temperatura e pressão o volume de um mol de gás ideal ocupa um volume de $$\color{Brown}{V_{N} = 22,4\,l}$$
Lei de Dalton das pressões parciais nas misturas gasosas.
John Dalton nasceu em 1766 e viveu até 1844. Entre uma vasta gama de contribuições para as ciências, temos para este momento de nosso conteúdo a lei acima citada. Seu enunciado é:
“A pressão total de uma mistura de gases em um recipiente é igual a somatória das pressões parciais de todas as frações dos diferentes gases da mistura”.
Pressão Parcial – supondo que em um cilindro existe uma mistura de $n$ gases. Se retirássemos todos os demais, deixando somente um dos gases no cilindro, à mesma temperatura, teríamos uma pressão bastante inferior. Esta seria a pressão parcial do gás remanescente. Se fizermos isso com cada uma das porções, teremos determinadas as pressões parciais de todos eles. Mais fácil dizer do que fazer, mas esse raciocínio nos permite escrever a seguinte relação:
$$\color{Navy}{p_{total}= p_{1} + p_{2} + p_{3} + … + p_{n}}$$
$$\color{NavyBlue}{p_{t} = \sum_{i}^{n} p_{i}}$$
Da equação geral dos gases podemos obter:
$\color{Maroon}{\frac{p_{t}\times V}{T} = \frac{p_{1}\times V_{1}}{T_{1}} + \frac{p_{2}\times V_{2}}{T_{2}} + … + \frac{p_{n}\times V_{n}}{T_{n}}}$
$$\color{Navy}{\frac{p_{t}\times V}{T} = \sum_{i}^{n}\frac{p_{i}\times V_{i}} {T_{i}}}$$
Exemplo prático – o ar com que inflamos os pneus de nossos automóveis e outros dispositivos similares, é uma mistura de gases, principalmente oxigênio e nitrogênio, na proporção de 20% e 80%. O compressor introduz essa mistura numa pressão de $\color{Maroon}{p = 2\,atm}$.
Aplicando o raciocínio ao ar contido no pneu nestas condições, temos que a pressão do oxigênio presente na fração de 20%, é de $\color{Maroon}{p_{O_2}= 0,4\,atm}$ e a pressão do nitrogênio na fração de 80% é de $\color{Maroon}{p_{N_2}=1,6\,atm}$.
A pressão total é: $$\color{Red}{p_{t} = p_{O_2} + p_{N_2}}$$
Isso resulta em: $p_{t} = 0,4 + 1,6 = 2,0\,atm$
Se temos dois gases contidos em recipientes distintos e mantidos à mesma temperatura. Um cilindro contém Hélio (H_{e}) e o outro contém Oxigênio (O_{2}). Podemos considerar que esses fases são ideais. Se misturarmos partes diferentes dos mesmos em um recipiente de volume V, teremos ao final uma pressão total que é igual à somatória das pressões parciais dos gases misturados.
$$\color{Sepia}{p_{t} = p_{He} + p_{O_2}}$$
Utilizando a equação de estado dos gases, teremos:
$$\color{Maroon}{p_{He}\times V = n_{He}\times RT}$$
$$\color{Maroon}{p_{O_2}\times V = n_{O_2}\times RT}$$
A pressão total será a soma das partes:
$$\color{Navy}{p_{t} = \sum_{i}^{Z}\frac{nRT}{V}}$$
Podemos aplicar o mesmo raciocínio para uma mistura de tantos gases quantos houver no interior do recipiente que contém a mistura.
O que vimos acima permite determinar a fração molar de um dos componentes da mistura. Basta dividir a equação de estado de cada parcela da mistura pela equação de estado da mistura toda.
$\frac{p_{H_e}\cdot V}{p_{t}\cdot V} = \frac{n_{H_e}\cdot RT}{\sum nRT}$
Simplificando os fatores comuns entre numeradores e denominadores resta:
$\frac{p_{H_e}}{p_{t}} = \frac{n_{H_e}}{\sum n} = X_{H_e}$
Do mesmo modo para (O_{2}):
$\frac{p_{O_2}}{p_{t}} = \frac{n_{O_2}}{\sum n} = X_{O_2}$
Podemos generalizar para uma mistura qualquer e para cada porção de gás da mistura:
$$\color{Navy}{X_{i} = \frac{p_{i}}{p_{t}} = \frac{n_{i}}{\sum n}}$$
É fácil notar que a soma de todas as frações molares da mistura será sempre igual a unidade.
$$\color{Navy}{\sum_i^Z {X_{i}} = 1}$$
Retomando o exemplo do pneu com pressão total $p_{t} = 2\, atm$, tendo $20\%$ de (O_{2}) e $80\%$ de (N_{2}). Podemos considerar que para cada mol da mistura temos $0,2\, mol$ de (O_{2}) e $0,8\,mol$ de (N_{2}). O que nos permite calcular as frações molares.
$X_{O_2} = \frac{0,2}{1} = 0,2$
$X_{N_2} = \frac{0,8}{1} = 0,8$
O que nos fornece a soma:
$$\color{Navy}{X_{t}= X_{O_2} + X_{N_2} = 0,2 + 0,8 = 1,0}$$
O conceito das pressões parciais é extremamente importante no nosso sistema respiratório. O sangue transporta oxigênio (O_2) para as células do nosso corpo, recebido no pulmão que o retira do ar inspirado. No retorno traz gás carbônico (CO_2), para ser liberado com o ar expirado para o ambiente. Isso é possível por conta da diferença de pressão desses gases no sangue e no interior das células. O sentido da transferência é da maior pressão para a menor.
E nesse ponto que reside a dificuldade encontrada pelos alpinistas e mergulhadores. A pressão do oxigênio fica menor do que o habitual e exige por isso o uso de equipamentos de suplementação como cilindros de ar comprimido enriquecido com oxigênio.
Tomemos a questão da pressão do ar atmosférico na Bolívia. O ar que respiramos ao nível do mar é uma mistura de gases, em que os principais são o nitrogênio, que corresponde a cerca de $80\%$ da composição do ar; e o oxigênio, que corresponde a quase $20\%$ do ar, e a pressão é de $p_{mar}= 100 000\,Pa$. Em La Paz, porém, a pressão atmosférica é igual $p_{Lp}= 60 000\,Pa$ e a porcentagem de gás oxigênio é $40\%$ menor que ao nível do mar. Vamos calcular, então, a pressão parcial do oxigênio e a porcentagem dele em volume no ar de La Paz:
- Ao nível do mar, temos:
- $X_{O_2} = \frac{20\%}{100\%} = 0,2$
A pressão parcial então é:
- $p_{O_2} = 0,2\times{100000}= 20.000\,Pa$
Vemos que ao nível do mar a pressão parcial do oxigênio é $20.000\,Pa$.
Em La Paz, a porcentagem de gás oxigênio é $40\%$ menor que ao nível do mar, o que equivale a dizer que sua pressão parcial é $60\%$ da pressão ao nível do mar.
$P_{O2L}= 0,6\times 20.000 = 12000 Pa$
Calculemos a porcentagem em volume do oxigênio no ar de La Paz:
$\% = 100\times\frac{12000}{60000} = 20\%$
Para completar, vamos analisar a fração volumétrica de um gás numa mistura.
Lei de Amagat
O químico francês Èmile Amagat(1845-1915) analisou a fração volumétrica da mistura ocupada por dada um dos gases componentes. Sem alterar a pressão e temperatura ele definiu:
“O volume que um gás ocupa em uma mistura, é exatamente igual ao volume que ocuparia se estivesse sozinho em um recipiente, nas mesmas condições de pressão e temperatura”.
Consideremos um recipiente de $V_{t}=50\,L$, contendo três gases genéricos A, B e C. O volume percentual que eles ocupam é respectivamente $V_{A_\%}=60\%$, $V_{V_\%}=25\%$ e $V_{C_\%} =15\%$. Na mesma temperatura e pressão da mistura os gases ocupam os volumes:
$V_{A_\%} = frac{V_{A}\times {100}}{V}$$\Leftrightarrow$$ 60 = \frac{V_{A}\times {100}}{50}$
$$\color{Maroon}{V_{A}= \frac{60\times 50}{100} = 30\,L}$$
Igualmente para os gases B e C:
$$\color{Maroon}{V_{B} =\frac{25\times 50}{100} = 12,5\,L}$$
$$\color{Maroon}{V_{C} =\frac{15\times 50}{100} = 7,5\,L}$$
Daí concluímos que:$V_{t} = V_{A} + V_{B} + V_{C} = 30 + 12,5 + 7,5 = 50\,L$
Generalizando ficamos com:
$$\color{Maroon}{V_{t} = \sum_{i}^{z} {V_{i}}}$$
Exemplo 1. Qual o volume parcial do gás nitrogênio (N_{2}) em 5 L de uma mistura com 40% de N_{2} em volume?
$V_{N_2}= \frac{5\times 40}{100}= 2,0\,L$
Podemos também utilizar a Equação de Clapeyron para obter as frações volumétricas.
$$\color{Brown}{pV = nRT}$$
Para as parciais: $V_{A} = \frac{n_{A}RT}{p}$
$V_{t} = \frac{\sum_{i}^{z}n_{i}RT}{p}$
A divisão do volume parcial pelo total fornece a fração material do gás na mistura
$X_{A} = \frac{V_{A}}{V_{t}} = \frac{\frac{n_{A}RT}{p}}{\frac{\sum_{i}^{z}n_{i}RT}{p}}$
Simplificandos os fatores comuns fica:
$X_{A} = \frac{V_{A}}{V_{t}} = \frac{n_{A}}{\sum_{i}^{z}{n_{i}}}$
Generalizando para qualquer um dos gases:
$$\color{Navy}{X = \frac{V_{i}}{V_{t}} = \frac{n_{i}}{\sum_{i}^{z} n_{i}}}$$
Um recipiente de capacidade de $V_{t}=41\,L$ apresenta 3 mol de gás hidrogênio (H_{2}), 2 mol de gás oxigênio (O_{2}) e 5 mol de gás metano (CH_{4}). Determine os volumes parciais de cada um dos gases dessa mistura.
Dados: $V_{t}=41\,L$, $n_{H_2}=3\,mol$, $n_{O_2}=2,0\,mol$, $n_{CH_4}=5\,mol$.
$$\color{Maroon}{n_{t}= 3,0 + 2,0 + 5,0 = 10,0\,mols}$$
Fração molar
$X_{H_2} =\frac{n_{H_2}}{n_{t}$$\Leftrightarrow$$X_{H_2} =\frac{3,0}{10,0}=0,3$
$X_{O_2}=\frac{2,0}{10,0} = 0,2$
$X_{CH_4}=\frac{5,0}{10,0} = 0,5$
$$\color{Brown}{V_{H_2}}{V_{t}}= X_{H_2}}$$
Dessa expressão tiramos:
$$\color{Brown}{V_{H_2} = X_{H_2}\times V_{t}}$$
$$\color{Navy}{V_{H_2} = {0,3}\times {10,0} = 3,0\,L}$$
$$\color{Navy}{V_{O_2}= {0,2}\times {10,0}= 2,0\,L}$$
$$\color{Navy}{V_{CH_4}= (0,5)\times{10,0} = 5,0\,L}$$
E agora?
É hora de fazer exercícios para sedimentar o que foi visto e completar a compreensão de todas as minúcias.
01. (UERJ – 2016) – Para descrever o comportamento dos gases ideais em função do volume V, da pressão P e da temperatura absoluta T, podem ser utilizadas as seguintes equações:
| Equação de Clapeyron | Equação de Stefan Boltzmann |
| $p\times V = n\times R\cdot T$ | $p\times V = N\times K\times T$ |
| $n$$\Rightarrow$ nº de mols | $N$$\Rightarrow$nº de moléculas |
| $R$$\Rightarrow$ constante dos gases | $K$$\Rightarrow$ constante de Boltzmann |
De acordo com essas equações, a razão $\frac{R}{K}$ é de um valor aproximado igual a quanto?
Dessas equações podemos tirar que?
$R = \frac{p\times V}{n\times T}$ (1)
$k = \frac{p\times V}{N\times T}$ (2)
Dividindo (1) por (2), membro à membro, teremos:
$\frac{R}{K} = \frac{\left(\frac{p\times V}{n\times T}\right)}{\left(\frac{p\times V}{N\times T}\right)}$$\Leftrightarrow$$\frac{R}{K} = \frac{\left(\frac{\not{p}\times\not{V}}{n\times\not{T}}\right)}{\left(\frac{\not{p}\times\not{V}}{N\times\not{T}}\right)}$
$\frac{R}{k} = \frac{\left(\frac{1}{n}\right)}{\left(\frac{1}{N}\right)}$$\Leftrightarrow$$\frac{R}{k}= \frac{1}{n}\times\frac{N}{1}$
$\frac{R}{k} = \frac{N}{n}$
Sabemos que $N = n\times{6,022}\times{10}^{23}$
$\frac{R}{k} = \frac{\not{n}\times{6,022}\times{10}^{23}}{\not{n}}$
$$\color{Brown}{\frac{R}{k} = 6,022\times{10}^{23}\,moléculas}$$
02. Qual deve ser a temperatura de certa quantidade de um gás ideal, inicialmente a 200\,K, para que tanto o volume quanto a pressão dupliquem?
Desejamos que: $ p = 2\times p_{0}$ e $V = 2\times V_{0}$
$$\color{Blue}{\frac{p_{0}\times V_{0}}{T_{0}} = \frac{p\times V}{T}}$$
$\frac{\not{p_{0}}\times\not{V_{0}}}{200} = \frac{2\times\not{p_{0}}\times 2\times\not{V_{0}}}{T}$$\Leftrightarrow$$\frac{1}{200}=\frac{4}{T}$
$T = 200\times 4 = 800 K$
$$\color{Brown}{T = 800\, K}$$
03. (Fuvest-SP) – O pneu de um carro estacionado tem uma pressão de $p_{0}= 2\,atm$, quando a temperatura é $\theta= 9^{0}C$. Depois do veiculo correr em alta velocidade, a temperatura do pneu sobe a $\theta = 37^{0}C$ e seu volume aumenta de $10\%$. Qual a nova pressão do pneu?
$p_{0}=2\,atm$
$T_{0} = 273,15 + 9 = 282,15\,K$
$T = 273,15 + 37^{0} = 310,15\,K$
$$\color{Brown}{V = 1,1 V_{0}}$$
$ p = ?$
$ p = ?$
$\frac{2\cdot V_{0}}{282} = \frac{p\times 1,1\times V_{0}}{310}$
$\frac{1}{141} = \frac{p\times 1,1}{310}$$\Leftrightarrow$$ p = \frac{341}{141}$
$$\color{Brown}{p = 2,418\,atm}$$
04. Um botijão de oxigênio de $V_{0} = 20\,L$ contém $n$ mols do gás a uma pressão de $p_{0}= 10\,atm$ e temperatura de $\theta_{0}= 27^{0}C$. Utilizou-se parte do gás, com o que a pressão caiu para $p = 6\,atm$ (à mesma temperatura). Quantos gramas do gás foram utilizados? Dado: $R = 0,082\,atm.l/mol.K$.
$T = 273 + 27 = 300\,K$
$$\color{Blue}{p\cdot V = n\cdot R\cdot T}$$
$10\cdot 20 = n_{0}\cdot 0,082\cdot 300$$\Leftrightarrow$$200 = 24,6\cdot n_{0}$
$n_{0} = \frac{200}{24,6} = 8,2\,mols$
Depois de gastar uma parte:
$ 6\times 20 = n\times 0,082\times 300$$\Leftrightarrow$$120 = 24,6 n$
$n = \frac{120}{24,6} =4,878\,mols$
Foram gastos em mols:
$\Delta n = n – n_{0}$$\Leftrightarrow$$\Delta n = 8,2 – 4,878 = 3,322 mols$
Se um mol de oxigênio tem massa $M = 16\,g$
$n = \frac{m}{M}$$\Leftrightarrow$$m = n\times M$
$$\color{Brown}{m = 3,322\times 16 = 53,152\, g}$$
05. Uma certa quantidade de gás ocupa um volume de $v_{0}=0,25\,m^{3}$ e sua temperatura é $T_{0}= 450\,K$. Sem que a pressão mude, sua temperatura é baixada para $T = 300\,K$. Determine o volume do gás nessa nova situação.
$\frac{V_{0}}{T_{0}} = \frac{V}{T}$
$\frac{0,25}{450} = \frac{V}{300}$$\Leftrightarrow$$V = \frac{0,25\cdot 300}{450}$
$V= \frac{75}{450}$$\Leftrightarrow$$ V= \frac{1}{6}= 0,111\, m^{3}$
$$\color{Brown}{V= 0,111\,m^{3}}$$
06. A $\theta_{0}= 27^{0}C$ determinada massa de gás ocupa o volume de $V_{0}=300\, mL$. Calcule o volume que essa massa ocupará se a temperatura se elevar a $\theta = 47^{0}C$, sem que haja variação de pressão.
$T_{0}= 273 + 27 = 300\,K $
$T = 273 + 47= 320\,K$
$\frac{V_{0}}{T_{0}} = \frac{V}{T}$$\Leftrightarrow$$\frac{300}{300} = \frac{V}{320}$
$$\color{Brown}{V = 320\,ml}$$
07. Certa quantidade de um gás ideal ocupa um volume de $V_{0}= 30\, litros$ à temperatura de $\theta_{0}=77^{0}C$ e sob pressão de $p_{0}=2,0 atm$. Responda: a) Qual o volume dessa quantidade de gás sob pressão $p= 8,0 atm$ à temperatura de $\theta= 427^{0}C$? b) Em que temperatura, expressa, em graus Celsius, o volume do gás será $V= 120\,litros$, mantida a pressão de $p =2,0\,atm?
$T_{0}= 273 + 77 = 350\,K$
$T = 273 + 427 = 700\, K$
a)$\frac{p_{0}\times V_{0}}{T_{0}}=\frac{p\times V}{T}$$\Leftrightarrow$$\frac{2\times 30}{350} = \frac{8\times V}{700}$
$\frac{60\times 700}{350} = 8\times V$$\Leftrightarrow$$\frac{120}{8}= V$
$$\color{Brown}{V = 15\,litros}$$
b) $$\color{Brown}{\frac{V_{0}}{T_{0}} = \frac{V}{T}}$$
$\frac{30}{350} = \frac{120}{T}$$\Leftrightarrow$$T = \frac{120\cdot350}{30} = 1400\, K$
$$\color{Brown}{\theta = 1400 – 273 = 1127^{0}C}$$
08. Uma mistura gasosa é formada por 14,2 gramas de gás cloro (Cl_{2}) e 13,2 gramas de gás carbônico (CO_{2}) Quais são as pressões parciais desses componentes supondo que a pressão total da mistura é de 2 atm? Dados: Massa molar do gás cloro = 71 g/mol; Massa molar do gás carbônico = 44 g/mol.
$M_{Cl_2} = 71\, g/mol$, $M_{CO_2}= 44\,g/mol$
$$\color{Maroon}{n = \frac{m}{M}}$$
$n_{Cl_2} = \frac{14,2}{71} = 0,2\, mols$
$n_{CO_2} = \frac{13,2}{44} = 0,3\,mols$
$n_{total}= n_{Cl_2} + n_{CO_2} = 0,2 + 0,3 = 0,5\, mols$
As frações molares serão:
$X_{CL_2} = \frac{n_{CL_2}}{n_{total}}$$\Leftrightarrow$$X_{Cl_2} = \frac{0,2}{0,5} = 0,4$
$$\color{Brown}{X_{Cl_2}= 40\%}$$
$X_{CO_2} = \frac{n_{CO_2}}{n_{total}}$$\Leftrightarrow$$X_{C)_2}=\frac{0,3}{0,5} = 0,6$
$$\color{Brown}{X_{CO_2} = 60\%}$$
As pressões parciais serão então:
$$\color{Navy}{p_{Cl_2} = 2\times {0,4} = 0,8\, atm}$$
$$\color{Navy}{p_{CO_2} = 2\times {0,6} = 1,2\, atm}$$
09.Um sistema apresenta uma mistura gasosa contendo $30\%$ de gás oxigênio (O_{2}), $50\%$ de gás propano (C_{3}H_{8}) e $20\%$ de monóxido de carbono (CO). Sabendo que a pressão total do sistema é de $p_{t}= 65000\,Pa$, determine o valor da pressão parcial de cada um dos gases.
$$\color{Maroon}{\frac{p_{i}}{p_{t}} = X_{i}}$$
$$\color{Maroon}{X_{i} = \frac{i\%}{100\%}}$$
$X_{O_2} = \frac{30\%}{100\%} = 0,3 $
$X_{C_{3}H_{8}}= \frac{50\%}{100\%}= 0,5$
$X_{CO} = \frac{20\%}{100\%} = 0,2 $
Temos as frações molares e podemos então usar a primeira equação para calcular as pressões parciais.
$\frac{p_{O_2}}{p_t} = X_{O_2}$$\Leftrightarrow$$\frac{p_{O_2}}{65000} = 0,3$
$$\color{Navy}{p_{O_2}= 19500\, Pa}$$
$$\color{Navy}{p_{C_{3}H_{8}} = 0,5\times {65000}= 32500\,Pa}$$
$$\color{Navy}{p_{CO} = 0,2\times{65000} = 13000\,Pa}$$
Exercícios por resolver
01. (UFRN) – A temperatura de uma certa quantidade de gás ideal, à pressão de $p_{0} = 1\,atm$, cai de uma temperatura de $T_{0}=400\,K$, para $T = 320\,K$. Se o volume permaneceu constante, a nova pressão é de:
( )a) 0,8\,atm; ( )b) 0,9\,atm; ( )c) 1,0\,atm; ( )d) 1,2\,atm; ( )e) 1,5\,atm.
02. (Mackenzie-SP) – Um gás perfeito tem volume de $V_{0}=300\,cm^{3}$ a certa pressão e temperatura. Duplicando simultaneamente a pressão e a temperatura absoluta do gás, o seu volume passará a ser:
( )a)$450\,cm^{3}$; ( )b) $300\,cm^{3}$; ( )c) $600\,cm^{3}$;
( )d)$900\,cm^3$; ( )e)$1200\,cm^{3}$.
03. (UFAL 84) – Um gás perfeito é aquecido dentro de um recipiente rígido e fechado. Nessas condições, sua pressão é:
( )a) inversamente proporcional à sua temperatura absoluta;
( )b) diretamente proporcional à sua temperatura absoluta;
( )c) constante;
( )d) inversamente proporcional à sua temperatura medida na escala Celsius;
( )e)diretamente proporcional à sua temperatura medida na escala Celsius.
04. (UFAL 87) – Um gás é mantido a volume constante. Se a sua temperatura aumentar qual das alternativas abaixo ocorrerá em relação à VELOCIDADE MÉDIA DAS MOLÉCULAS e PRESSÃO DO GÁS respectivamente:
( )a) aumente – diminui;
( )b) diminui – aumenta;
( )c) permanece constante – permanece constante;
( ) d) aumenta – aumenta;
( )e) diminui – diminui.
05. (IBERO AMERICANA-SP 94) – Num recipiente fechado, encontramos 10 mols de um gás perfeito que ocupam um volume $v_{0}= 4\, l$ à temperatura de $\theta=127^{0}C$. Pede-se a pressão exercida por esse gás. Daddo: (Constante Universal dos gases perfeitos $R = 0,082 atm\cdot l/mol\cdot K$).
( )a) 1\,atm; ( )b) 82\,atm; ( )c) 41\,atm; ( )d) 10\,atm; ( )e)100\,atm.
06. (FUMEC 94) – Uma determinada massa de um gás ideal sofre uma transformação isotérmica. Se a pressão final for o dobro da inicial, pode-se airmar que:
( ) a) todas as alternativas estão erradas;
( ) b) o volume permaneceu constante;
( ) c) a temperatura final é igual a duas vezes a temperatura inicial;
( ) d) o volume final é igual a duas vezes o volume inicial;
( ) e) o volume foi reduzido à metade.
07. (UEL 91) – As afirmativas abaixo referem-se a situações onde a temperatura é $\theta=0^{0}$ e a pressão é $p = 1,0\,atm$.
I – Um mol de uma substância sólida ocupa um volume igual a 22,4 litros.
II – Um mol de uma substância líquida ocupa um volume igual a 22,4 litros.
III – Um mol de um gás perfeito ocupa um volume igual a 22,4 litros.
Pode-se afirmar que somente:
( )a) III é correta; ( )b) II é correta; ( )c) I é correta; ( )d) I e II são corretas;
( )e) II e III são corretas.
08. (UFPB 94) – Um mol de $H_{e}$ e dois mols de Ar estão dentro de um recipiente cujo volume é 3 litros. A temperatura é $\theta = 27^{0}C$. Usando-se $R=0,08 atm\cdot l/mol\cdot K$, o valor da pressão sobre as paredes do recipiente é:
( )a) 0,8 atm; ( )b) 12 atm; ( )c) 24 atm; ( )d) 1,6 atm; ( )e) 3,0 atm.
09. (U.F.Santa Maria-RS) – Uma bolha de gás ideal com volume V, é solta do fundo de um lago, onde a pressão é o dobro da pressão existente na superfície. Suponha a temperatura da água constante, a bolha chegará à superfície, com um volume:
( )a)$\frac{V}{3}$; ( )b) $\frac{V}{2}$; ( )c) $2\cdot V$; ( )d) $V$; ( )e)$\frac{3\cdot V}{2}$.
10. (UFAC) – Assinale a que temperatura temos de elevar o volume $V_{0} = 400\, ml$ de um gás ideal a $\theta = 15^{0}C$ para que o seu volume atinja o valor de $V = 500\, ml$, sob pressão constante.
( )a) $25^{0}C$; ( )b) $49^{0}C$; ( )c) 87^{0}C$; ( )d) 69^{0}C; ( )e) 110^{0}C$
11. (EEP) – Um gás está contido em um cilindro de volume V com pressão de $p_{0} = 1\, atm$ e temperatura de $\theta = 25^{0}C$. Esse cilindro possui uma válcula de segurança que libera o gás quando a pressão exercida é de $p = 5\, atm$. Qual é a temperatura máxima que esse gás pode ter sem que haja liberação de gás?
( )a) $125^{0}C$; ( )b) $25^{0}C$; ( )c) $50^{0}C$; ( )d) $200^{0}C; ( )e) 1217^{0}C.
12. (PUC-SP) – Sabe-se que um gás mantido num recipiente fechado exerce determinada pressão, consequente ao choque das moléculas gasosas conra as paredes do recipiente. Se diminuirmos o volume do recipiente e mantivermos constante a temperatura, a pressão do gás:
( )a) não sofrerá alteração; ( )b) diminuirá; ( )c) aumentará; ( )d) dependendo do gás aumentará ou diminuirá. ( )e)N.d.a.
13.(UNEB-BA) – Em condições tais que um gás se comporte como ideal, as variáveis de estado assumem os valores $T_{0}= 300\, K$, volume $V_{0}=2,0 m^{3}$ e pressão de $p_{0} = 40000\, Pa$, num estado A. Sofrendo certa transformação, o sistema chega ao estado B, em que os valores são $T= 450\, K$, o volume é $V= 3,0\, m^{3}$ e a pressão é $P$. O valor de P, em pascal é:
( )a) 13000; ( )b) 40000; ( )c) 27000; ( )d) 60000; ( )e) 120000.
14. (PUC-MG) – Um balão meteorológico foi inflado com hidrogênio, adquirindo um volume $V_{0}$, em um local onde a temperatura ambiente é $\theta_{0} = 27^{0}C$ e a pressão atmosférica, e a pressão é de $p_{0}=1\, atm$. A certa altura em relação ao solo, verifica-se que o seu volume aumentou 20% do volume inicial $V_{0}$, e a temperatura alcançou $\theta = -21^{0}C$. Com base nesses dados, é possível afirmar que a pressão do ar, em atmosferas, naquela altitude, é igual:
( )a) 0,8; ( )b) 0,4; ( )c) 0,6; ( )d) 0,5; ( )e) 0,7.
15. (ITA-SP) – Determine a massa de gás hélio contida num balão, sabendo que seu peso molecular é igual a 4, a constante de Clapeyron vale $R = 0,082 atm\cdot l/mol\cdot K$ e que o gás ocupa um volume igual a $V=5 m^{3}$, numa temperatura de $\theta =23^{0}C$ e uma pressão $p = 30\, cmHg$.
( )a) 1,86 g; ( )b)46 g; ( )c) 96 g: ( )d)390 g; ( )e)186 g.
16. (Acafe-SC) – Complete o enunciado com a alternativa verdadeira dentre as relacionadas a seguir.
Afirma-se que moléculas de diferentes gases perfeitos, a mesma temperatura, têm em média ________________________.
( )a) mesmo impulso; ( )b) mesma aceleração; ( )c) mesma energia cinética; ( )d)mesma quantidade de movimento; ( )e)mesma velocidade.
17. (UFU-MG) – As grandezas que definem completamente o estado de um gás são:
( )a) temperatura, pressão e volume; ( )b) apenas volume e temperatura; ( )c) massa e volume; ( )d)somente pressão e volume; ( )e)massa, pressão, volume e temperatura.
18. (OSEC-SP) – Volumes iguais de gases nas mesmas condições de temperatura e pressão:
( )a) possuem o mesmo potencial de ionização;
( )b)possuem a menor densidade; ( )c) possuem a mesma massa;
( )d) contém o mesmo número de moléculas;
( )e) nenhuma resposta é correta.
19.(UEPG-PR) – 2560 g de oxigênio, cuja molécula-grama é 32 g, ocupam 2 litros de volume num recipiente à temperatura de $\theta =-23^{0}C$. Sendo dado $R = 0,082 atm\cdot l/mol\cdot K$, a pressão no interior do recipiente terá um valor de:
( )a)20 atm; ( )b) 200 atm; ( )c) 0,2 atm; ( )d)0,02 atm; ( )e)N.d.a.
20. (MACK-SP) – Num recipiente fechado e indeformável, temos 1 mol de oxigênio (M = 16 g) sob determinadas condições de pressão e temperatura. Introduzindo-se mais 80 g de oxigênio nesse recipiente e mantendo-se constante a temperatura, a pressão do gás:
( )a) reduz-se à metade da inicial; ( )b) dobra; ( )c) aumenta seis vezes;
( )d) aumenta cinco vezes; ( ) e) mantém-se constante.
21. (FURG) – Um gás ideal sofre uma transformação isobárica. Qual dos gráficos abaixo, onde V representa volume e T representa temperatura absoluta, melhor representa essa transformação?
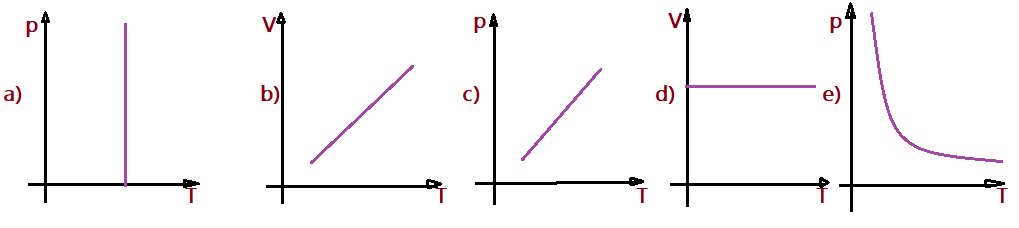
22. (UPE-2011-Q1) – Em relação à teoria cinética molecular dos gases, é CORRETO afirmar que:
a) a energia cinética média de um conjunto de moléculas de um gás depende, apenas e exclusivamente, das massas das moléculas desse gás.
b) quando quadruplicamos a temperatura absoluta de um conjunto de moléculas de um gás, suas moléculas terão velocidade média quadruplicada.
c) quanto maiores as interações entre as moléculas de um gás, mais rigorosamente ele se comportará como um gás ideal.
d) numa mesma temperatura, independentemente das massas molares de cada gás, as moléculas têm energias cinéticas médias iguais.
e) as colisões entre moléculas de um gás perfeito com as paredes do recipiente que as contém são inelásticas para qualquer tipo de gás ideal.
23. De acordo com a teoria cinética dos gases, é incorreto afirmar:
a) Energia cinética média é proporcional à temperatura de Kelvin;
b) As partículas estão muito unidas e têm baixa velocidade;
c) As partículas ocupam todo o volume disponível e têm
movimento livre;
d) As partículas possuem alta velocidade e ocorrem choques entre elas
e contra as paredes do recipiente que as contém;
e) As partículas têm movimento desordenado.
24. A lei de Boyle afirma que, mantendo-se a temperatura constante, a pressão P e o volume V de um gás relacionam-se da seguinte maneira:
a) P e V são diretamente proporcionais;
b) P + V = constante;
c) P – V = constante;
d) P = V;
e) Se P for reduzido à metade, o valor de V deverá dobrar.
25. (Fuvest-SP) – Se um certo gás contido em um compartimento e exercendo pressão de $p_{0}=10\,cmHg for comprimido de maneira a ocupar um vigésimo do seu volume inicial, qual será a pressão final (temperatura constante)?
26. Sob pressão de $p_{0}=5,0\, atm$, certa massa de gás perfeito ocupa o volume de $V_{0}= 50\, litros$ à temperatura de $T_{0}= 100\, K$. Responda: a) Sob que pressão o gás passa a ocupar o volume de $V=100\, litros$, quando sua temperatura for modificada para $T =400\, K$? b) Em que temperatura o volume do gás será de $V_{1}=20\,litros$, se a pressão for modificada para $p_{1}= 2,0 atm$? c) Que volume o gás passará a ocupar se a temperatura for alterada para$T_{1}= 200\,K$ e a pressão para $p =4,0\, atm$?
27. O estado inicial de determinada quantidade de gás perfeito é caracterizado pelos valores $V_{1}= 5,0\, litros$ para o volume, $p_{1} = 3,0\, atm$ para a pressão e $T_{1} = 50\,K$ para a temperatura. Determine: a)a pressão final, sob a qual o volume é $V_{2} = 10\,litros$ e a temperatura é $T_{2} = 400\,K$; b) a temperatura em que o gás ocupa o volume $V_{3} = 15\,litros$ sob pressão $p_{3} = 1,0\, atm$.
28. (Furg-RS) O ar é uma mistura de gases. Mais de 78% dessa mistura é de nitrogênio. O oxigênio representa cerca de 21%. O argônio 0,9% e o dióxido de carbono, 0,03%. O restante é constituído de outros gases. O volume ocupado pelo oxigênio nessa mistura, em um ambiente de 10 L, é:
a) 2,1 L
b) 4,7 L
c) 10 L
d) 17,7 L
e) 22,4 L
29.(Unifor-CE) Em um recipiente de 1,0 L, há um sistema gasoso em equilíbrio, contendo três gases A, B e C. Suas pressões parciais são, respectivamente, 0,2 atm, 0,5 atm e 0,7 atm. Sobre esse sistema pode-se afirmar que
I. a pressão total do sistema é 1,4 atm.
II. o gás A tem o menor volume molar parcial.
III. o gás C contribui com o maior número de moléculas na mistura.
É verdadeiro o que se afirma em
a) I, somente.
b) III, somente.
c) I e II, somente.
d) II e III, somente.
e) I, II e III.
30.Um recipiente contém 29 g de butano (C4H10) e 88 g de dióxido de carbono (CO2). Sabendo que a pressão total da mistura é igual a 20 atm, qual é a pressão parcial, em atm, exercida pelo butano? (Massas atômicas: C = 12; H = 1; O = 16)
a) 5 atm.
b) 3 atm.
c) 2 atm.
d) 4 atm.
e) 6 atm.
31.Em um certo balão de $V= 50\,L$ de capacidade, mantido em temperatura constante de $T=75\,K$, são colocados $V_{N_2}=27,5\,L$ de nitrogênio a $p_{N_2}=1,25\,atm$ e $\theta_{N_2}= 14,25^0C$, $V_{O_2}=20\,L$ de oxigênio a$p_{O_2}= 0,625\,atm$ e$\theta_{O_2}= –5,75^0C$ e $V_{Neon}=12,5\,L$ de neônio a $p_{Neon}=0,8\,atm$ e $\theta_{Neon}=11,75^0C$. A pressão total da mistura gasosa, em atmosfera, é:
a) 0,50
b) 0,10
c) 0,20
d) 0,40
e) 0,30
Se tiver alguma dificuldade para resolver, use um dos canais abaixo listados e pergunte, nem que seja sobre exercícios ou problemas que sejam de outra origem.
Curitiba, 25 de maio de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
