Física – Termologia, Dilatometria.
O que é dilatometria?
Sabemos que as moléculas de um corpo qualquer não estão em repouso. Elas, exceto na situação do que chamamos “zero absoluto”, estão sempre executando um movimento de vibração (oscilação) em torno de sua posição de equilíbrio. Na medida em que a temperatura se eleva, essa oscilação aumenta de amplitude. A frequência em geral permanece constante. Esse aumento da amplitude implica num aumento da energia cinética durante o movimento de oscilação.
Torna-se fácil entender por que o corpo, submetido a uma elevação de temperatura, sofre um aumento em suas dimensões físicas como o comprimento, a área e o volume. O aumento da amplitude de dos movimentos vibratórios das moléculas, exige mais espaço, o que faz as moléculas do interior “empurrar” as outras mais para fora. O resultado é a variação das dimensões. A disposição relativa das moléculas permanece igual, apenas as distâncias entre elas aumenta.
Classificação da dilatação
- Dilatação linear: – quando a dilatação em uma dimensão (comprimento) predomina sobre as demais. Não significa que as outras dimensões não sofram dilatação na mesma proporção, apenas suas medidas são muito menores do que o comprimento, tornando-se assim menos importantes e determinadas circunstâncias.
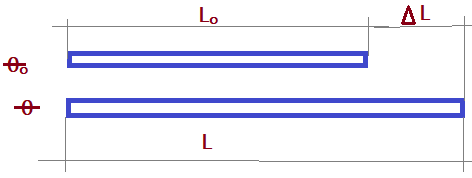
Seja uma haste de comprimento $L_{0}$, à temperatura $\Theta_{0}$. Ao ser aquecida à temperatura $\Theta$, seu comprimento aumenta até o valor $L$. Dessa forma temos duas grandezas variando. Há um fator que depende da natureza do material de que é feita a hasta, representado pela letra $\alpha$ e recebe o nome Coeficiente de dilatação linear. Podemos determinar experimentalmente que a variação de comprimento é proporcional aos três fatores: comprimento inicial, variação de temperatura e coeficiente de dilatação linear.
$$\color{Blue}{\Delta L = \alpha\cdot L_{0}\cdot \Delta\theta}$$
O comprimento final é obtido pela adição do comprimento inicial ao acréscimo causado pela dilatação.
$$\color{Blue}{L = L_{0} + \Delta L}$$
$$\color{Blue}{L = L_{0} + \alpha\times L_{0}\times \Delta\theta}$$
$$\color{Blue}{L = L_{0}\left(1 + \alpha\times\Delta\theta\right)}$$
Unidades e valores do coeficiente de dilatação linear.
$$\color{Blue}{\Delta L = \alpha\times L_{0}\times\Delta\Theta}$$
$\alpha = \frac{\Delta L}{L_{0}\times\Delta\Theta}$
No sistema SI: $\alpha= ^{0}C^{-1} \lor \alpha = K^{-1}$
Nos demais sistemas de unidades também usaremos essa mesma unidade.
| Substância | $\alpha = ^{0}C^{-1}$ |
| Porcelana | $3\times{10}^{-6}$ |
| Vidro comum | $8\times{10}^{-6}$ |
| Platina | $9\times{10}^{-6}$ |
| Aço | $11\times{10}^{-6}$ |
| Concreto | $12\times{10}^{-6}$ |
| Ferro | $12\times{10}^{-6}$ |
| Ouro | $15\times{10}^{-6}$ |
| Cobre | $17\times{10}^{-6}$ |
| Prata | $19\times{10}^{-6}$ |
| Alumínio | $22\times{10}^{-6}$ |
| Zinco | $26\times{10}^{-6}$ |
| Chumbo | $27\times{10}^{-6}$ |
2. Dilatação superficial: – uma chapa de material sólido, principalmente as metálicas, tendo uma superfície $S_{0}$ na temperatura $\theta_{0}$. Ao aquecê-la até a temperatura final $\theta$, sofre uma dilatação de valor $\Delta\theta$. Adicionando a superfície inicial ao acréscimo de superfície causada pela dilatação, temos o seu valor final.
$$\color{Blue}{\Delta S = \beta\times S_{0}\times\Delta\theta}$$
$$\color{Blue}{S = S_{0} + \Delta S}$$
$$\color{Blue}{S = S_{0} + \beta\times L_{0}\times\Delta\theta}$$
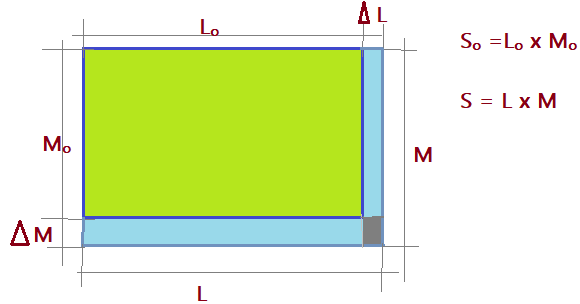
Sabemos que a área de uma superfície retangular é dada pelo produto entre o comprimento e a largura. Assim:
$$\color{Blue}{S_{0} = {L_{0}\times M_{0}}}$$
$$\color{Blue}{S = L\times M}$$
Substituindo $L$ e $M$ pelas expressões de sua dilatação, teremos:
$S = \left({L_{0} + \alpha\times L_{0}\times\Delta\theta}\right)\times\left({M_{0} + \alpha\times M_{0}\times\Delta\theta}\right) $
$S={L_{0}\times M_{0}} + {L_{0}\times\alpha\times M_{0}\times\Delta\theta} + {M_{0}\times\alpha\times L_{0}\times\Delta\theta} + {\alpha}^{2}\times L_{0}\times M_{0}\times{\Delta\theta}^{2}$
No termo final da expressão, temos:
${\alpha}^{2}\times L_{0}\times M_{0}\times{\Delta\theta}^{2}$
Vimos na tabela de coeficientes de dilatação lineares acima que todos tem uma multiplicação por ${10}^{-6}$. Se elevarmos qualquer desses valores ao quadrado, este expoente ficará multiplicado por $2$. Isto torna o termo um milhão de vezes menor do que qualquer outro. Assim se o desconsiderarmos, isto é, fizermos igual a zero, ele será eliminado. Então:
$S = S_{0} + 2\times\alpha\times S_{0}\times\Delta\theta$
Comparando com a expressão da dilatação vista acima, podemos concluir que:
$$\color{Brown}{\beta = 2\alpha}$$
Para obter o coeficiente de dilatação superficial $\beta$, basta multiplicar o valor do linear por $2$.
3. Dilatação volumétrica: – sólido geométrico pode ter suas dimensões alteradas pelo aquecimento. Imaginemos um paralelepípedo com as medidas $L_{0}$, $M_{0}$ e $N_{0}$. A temperatura inicial é $\theta_{0}$ e provoca-se o aquecimento até ao valor $\theta$. O volume irá aumentar proporcionalmente ao volume inicial, da variação de temperatura e do coeficiente de dilatação volumétrico.
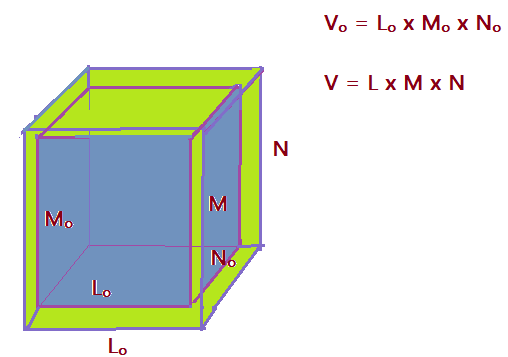
$$\color{Blue}{V_{0} = L_{0}\times M_{0}\times N_{0}}$$
$$\color{Brown}{\Delta V = \gamma\times V_{0}\times\Delta\theta}$$
$$\color{Brown}{V = V_{0} + \gamma\times V_{0}\times\Delta\theta}$$
$$\color{Brown}{V = V_{0}\left(1 + \gamma\times\Delta\theta\right)}$$
Se exprimirmos as três dimensões em sua fórmula de dilatação linear, teremos:
$V = {L_{0}\left(1 + \alpha\times\Delta\theta\right)}\times{M_{0}\left(1+ \alpha\times\Delta\theta\right)}\times{N_{0}\left(1 + \alpha\times\Delta\theta\right)}$
$V = {L_{0}\times M_{0}\times N_{0}}\times{1 + 3\times\alpha\times\Delta\theta + 3\times\alpha^{2}\times{\Delta\theta}^{2} + \alpha^{3}\times{\Delta\theta}^{3}}$
Da mesma forma como fizemos na dilatação superficial, os termos com expoente $2$ e $3$, tornam-se insignificantes e podem ser desprezados, restando pois:
$V = V_{0}\left(1 + 3\times\alpha\cdot\Delta\theta\right)$
De onde tiramos que:
$$\color{Brown}{\gamma = 3\times\alpha}$$
Obtemos os coeficientes de dilatação volumétrica multiplicando o linear por três. Podemos em verdade escrever a igualdade:
$$\color{Brown}{\frac{\alpha}{1} = \frac{\beta}{2} = \frac{\gamma}{3}}$$
Vamos exercitar o que aprendemos.
01. Uma haste de alumínio tem comprimento $L_{0}=120,0\,cm$, quando sua temperatura é $\theta_{0}= 20^{0}C$. Sendo o coeficiente de dilatação linear do alumínio igual a $\alpha = 22\cdot{10}^{-6}$, determine a dilatação e o comprimento final se for aquecida uniformemente à temperatura de $\theta = 100,0^{0}C$.
Dados: $L_{0} = 120,0\, cm$; $\theta_{0}=20^{0}$; $\theta = 100^{0}C$ e $\alpha = 22\cdot\left({10}^{-6}\right)^{0}C^{-1}$
a) $$\color{Blue}{\Delta L = \alpha\times L_{0}\times\Delta\theta}$$
$\Delta L = 22\times{10}^{-6}\times 120\times\left({100 – 20}\right)$
$\Delta L = 22\times 120\times 80\times {10}^{-6}$
$\Delta L = 211.200\times {10}^{-6} = 0,2112\,m$
$$\color{Brown}{0,2112\,cm}$$
b) $$\color{Blue}{L = L_{0}\left(1 + \alpha\times\Delta\theta\right)}$$
$L = 120\cdot\left(1 + 22\times{10}^{-6}\times{100 – 20}\right)$
$L = 120\times\left(1 + 0,001760\right)$$\Leftrightarrow$$L = 120,2112\,cm$
$$\color{Brown}{L = 120,2112\,cm}$$
02. Uma placa de ferro, de $S_{0}=2,36\,m^{2}$, está a $\theta_{0}=10^{0}C$. Sendo o coeficiente de dilatação linear do ferro igual $\alpha = 12\times\left({10}^{-6}\right)^{0}C^{-1}$ e a aquecemos a temperatura de $\theta=60^{0}C$. Determine: a) a área final da superfície; b) a dilatação térmica.
Dados:$S_{0} = 2,36\, m^{2}$; $\theta_{0}=10^{0}C$; $\theta=60^{0}C$; $\alpha=12\times\left({10}^{-6}\right)^{0}C^{-1}$
a) $$\color{Blue}{S = S_{0}\left(1 + 2\times\alpha\times\Delta\theta\right)}$$
$S = 2,36\times\left(1 + 2\times 12\times {10}^{-6}\right)$
$S = 2,36\times\ {1,000024} = 2,36005664\, m^{2}$$\Leftrightarrow$$\color{Brown}{S = 2,36005664\,m^{2}}$
b) $\color{Blue}{\Delta S = S – S_{0}}$
$\Delta S = 2,36005664 – 2,36 = 0,00005664\,m^{2}$
$$\color{Brown}{\Delta S = 56,64\times{10}^{-6}\,m^{2}}$$
03. Um bloco de chumbo $\alpha = 27\times{10}^{-6}/^{0}C$, tem volume de $V_{0}= 454\, cm^{3}$, quando sua temperatura é $\theta_{0}= 25^{0}C$. Aquecido a $\theta = 75^{0}C$, determine: a) a dilatação térmica sofrida pelo bloco; b) o volume final do bloco.
Dados: $\alpha = 27\times{10}^{-6}/^{0}C$; $V_{0} = 454\,cm^{3}$; $\theta_{0} = 25^{0}C$; $\theta =75^{0}C$.
a) $$\color{Blue}{\Delta V = 3\cdot\alpha\times V_{0}\times\left({75 – 25}\right)}$$
$\Delta V = 3\cdot 27\times{10}^{-6}\times 50$$\Leftrightarrow$$\Delta V = 4050\times{10}^{-6} = 0,00405\,cm^{3}$
$$\color{Brown}{\Delta V = 0,00405\,cm^{3}}$$
b)$$\color{Blue}{V = V_{0} + \Delta V}$$
$V = 454 + 0,00405$$\Leftrightarrow$$\color{Brown}{V = 454,00405\, cm^{3}}$
É sua vez agora
01. Um fio de aço apresenta comprimento igual a $L_{0}=20\,m$ quando sua temperatura é de $\theta_{0}=40 ^{0}C$. Qual será seu comprimento quando sua temperatura for igual a $\theta=100^{0}C$? Considere do coeficiente de dilatação linear do aço igual a $\alpha=11\cdot{10}^{-6}/^{0}C$.
02. Uma chapa quadrada de alumínio, possui lados iguais a $L_{0}=3\,m$ quando sua temperatura é igual a $\theta_{0}=80^{0}C$. Qual será a variação da sua área, se a chapa for submetida a uma temperatura de $\theta=100^{0}C$? Considere o coeficiente de dilatação linear do alumínio $\alpha =22\times{10}^{-6}/^{0}C$.
03. (VUNESP-SP) A dilatação térmica dos sólidos é um fenômeno importante em diversas aplicações de engenharia, como construções de pontes, prédios e estradas de ferro. Considere o caso dos trilhos de trem serem de aço, cujo coeficiente de dilatação é $\alpha = 11·10–^{-6}/ ^{0}C$ Se a $\theta_{0}=10^{0}C$ o comprimento de um trilho é de $L_{0}=30,0\,m$, de quanto aumentaria seu comprimento se a temperatura aumentasse para $\theta = 40^{0}C$
a) $11\times{10}^{–4}\,m$;
b) $33\times{10}^{–4}\,m$;
c) $99\times{10}^{–4}\,m$;
d) $132\times{10}^{–4}\,m$
e) $165\times{10}^{–4}\,m$.
04. (Mack–SP) – Uma placa de alumínio (coeficiente de dilatação linear do alumínio $\alpha = 22\times{10}^{–6} /^{0}C$, com $S_{0}=2,4\,m^{2}$ de área, à temperatura de $\theta_{0}={–20}^{0}C$, foi aquecido à $\theta=176^{0}F$. O aumento de área da placa foi de aproximadamente:
a) $24\,cm^{2}$;
b) $48\,cm^{2}$;
c) $63\,cm^{2}$;
d) $32\,cm^{2}$;
e) $144\,cm^{2}$.
05. (UFRS) Uma barra de aço e uma barra de vidro têm o mesmo comprimento à temperatura de $\theta_{0}= 0^{0}C$, mas, a $\theta= 100^{0}C$, seus comprimentos diferem de $\Delta L = 0,1\, cm$. Considere os coeficientes de dilatação linear do aço e do vidro, respectivamente, iguais a $\alpha_{aço}=12\times{10}^{–6}/^{0}C$ e $\alpha_{vid}=8\times{10}^{-6}/{0}C$.
Qual é o comprimento das duas barras à temperatura de $0^{0}C$?
a) 50 cm;
b) 83 cm;
c) 125 cm;
d) 250 cm;
e) 400 cm.
06. As deformações geralmente encontradas nos trilhos de trens podem ser explicadas por meio:
a) do desequilíbrio entre as forças internas e externas presentes no material;
b) das reações químicas que são favorecidas pelo aumento da temperatura dos trilhos;
c) do fenômeno da dilatação térmica;
d) do baixo ponto de fusão dos metais presentes nos trilhos;
e) da quantidade de calor latente recebido pelos trilhos.
07. (UFAL) O fato de barras de ferro contidas em uma viga de concreto não provocarem rachaduras no concreto pode ser explicado pela semelhança que existe entre os valores do:
a) calor específico desses materiais;
b) coeficiente de dilatação linear desses materiais;
c) coeficiente de atrito desses materiais;
d) calor de fusão desses materiais;
e) coeficiente de condutividade térmica desses materiais.
08. (Olimpíada Paulista de Física) – É muito comum acontecer, quando copos iguais são empilhados colocando-se um dentro do outro, de dois deles ficarem emperrados, tornando-se difícil separá-los. Considerando o efeito da dilatação térmica, pode-se afirmar que é possível retirar um copo de dentro do outro se:
a) os copos emperrados forem mergulhados em água bem quente;
b) no copo interno for despejada água quente, e o copo externo for mergulhado em água bem fria;
c) os copos emperrados forem mergulhados em água bem fria;
d) no copo interno for despejada água fria, e o copo externo for mergulhado em água bem quente;
e) não é possível separar os dois copos emperrados, considerando o efeito da dilatação térmica.
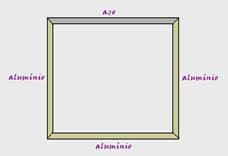
09. Uma moldura quadrada, feita com três hastes de alumínio e uma quarta de aço, encontra-se em equilíbrio térmico. O sistema é, então, submetido a um processo de aquecimento, de forma que a variação de temperatura é a mesma em todas as hastes.
Podemos afirmar que, ao final do processo de aquecimento, a figura formada pelas hastes estará mais próxima de um:
a) quadrado.
b) retângulo.
c) losango.
d) trapézio retângulo.
e) trapézio isósceles.
10. (FGV-SP) Um serralheiro monta, com o mesmo tipo de vergalhão de ferro, a armação esquematizada.

A barra transversal que liga os pontos A e B não exerce forças sobre esses pontos. Se a temperatura da armação for aumentada, a barra transversal:
a) continua não exercendo forças sobre os pontos A e B;
b) empurrará os pontos A e B, pois ficará $\sqrt{2}$ vezes maior que o novo tamanho que deveria assumir;
c) empurrará os pontos A e B, pois ficará $L_{0}\times\Delta\theta$ vezes maior que o novo tamanho que deveria assumir;
d) tracionará os pontos A e B, pois ficará $\sqrt{2}$ vezes menor que o novo tamanho que deveria assumir;
e) tracionará os pontos A e B, pois ficará $L_{0}\times\Delta\theta$ vezes menor que o novo tamanho que deveria assumir.
11. (UFRGS) – Quando se fornece calor a uma substância, podem ocorrer diversas modificações decorrentes de propriedades térmicas da matéria e de processos que envolvem a energia térmica.
Considere as afirmações abaixo, sobre processos que envolvem fornecimento de calor.
I. Todos os materiais quando aquecidos, expandem-se.
II. A temperatura de ebulição da água depende da pressão.
III. A quantidade de calor a ser fornecida, por unidade de massa, para manter o processo de ebulição é denominado calor latente de vaporização.
Quais estão corretas?
a) Apenas I;
b) Apenas II;
c) Apenas III;
d) Apenas II e III;
e) I, II e III.
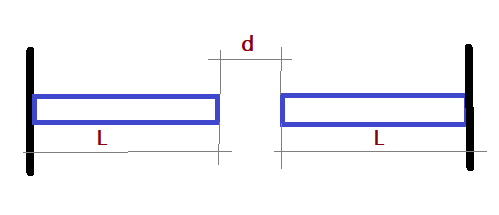
12. Uma barra de comprimento $L = 50\, m$, feita de um material X, sofre variação de temperatura de $\Delta\theta= 20^{0}C$, e seu comprimento varia em $0,02\%$. Considere duas barras do mesmo material $X$ e
de mesmo comprimento $L$, posicionadas, uma em frente à outra, separadas por uma distância $d = 1\,cm$ (veja a figura). Admitindo-se que cada barra cresça de forma homogênea, a variação de temperatura necessária para que a distância $d$, entre elas, se anule será igual a quanto?
13. Uma barra metálica de um material experimental, à temperatura $\theta_{A}$, tem comprimento $L_{A}$. Quando essa barra é aquecida à temperatura $\theta_{B}$, sendo $\theta_{B} >\theta_{A}$, tem comprimento $L_{B} = 1,331\times L_{A}$. Sabe-se que a cada aumento de temperatura de $\Delta\theta =20\,K$, a barra aumenta seu comprimento
em $10\%$. Então, é CORRETO afirmar que a diferença de temperatura $\theta_{B} – \theta_{A}$ é:
a) 55 K;
b) 50 K;
c) 65 K;
d) 60 K;
e) 80 K.
14. Um ferreiro deseja colocar um anel de aço ao redor de uma roda de madeira de $D= 1,200\,m$ de diâmetro. O diâmetro interno do anel de aço é $D_{i}=1,198\,m$. Sem o anel ambos estão inicialmente à temperatura ambiente de $\theta_{0}= 28 ^{0}C$. A que temperatura aproximadamente é necessário aquecer o anel de aço para que ele encaixe exatamente na roda de madeira? Use $\alpha = 11.10^{-6} /{0}C$.
a) $180^{0}C$;
b) $190 ^{0}C$;
c) $290 ^{0}C$;
d) $480^{0}C;
e) $450^{0}C$.
15. Uma chapa metálica de área $S_{0}=1,0 \,m^{2}$, ao sofrer certo aquecimento, dilata de $\Delta S = 0,36\,mm^{2}$. Com a mesma variação de temperatura, um cubo de mesmo material, com volume inicial de $V_{0}= 1,0\,dm^{3}$, dilatará:
a) $\Delta V = 0,72\,mm^{3}$;
b) $\Delta V = 0,54\,mm^{3}$;
c) $\Delta V = 0,36\,mm^{3}$;
d) $\Delta V = 0,27\,mm^{3}$;
e) $\Delta V = 0,18\,mm^{3}$
16. Duas barras metálicas A e B de um mesmo material e a uma mesma temperatura inicial, têm comprimento $L_{OA}$ e $L_{OB}= 3\times L_{OA}$. A seguir, varia‐se a temperatura da barra A de $\Delta\theta_{A}$, o que
faz a barra A sofrer uma variação comprimento por dilatação $\Delta L_{A}$. Para que a barra B sofra a mesma variação de comprimento da barra A, deve‐se variar a temperatura da barra B, de um valor $\Delta \theta_{B}$, igual a:
a) $3\cdot\Delta\theta_{A}$;
b) $\frac{1}{3}\times\theta_{A}$;
c) $\Delta\theta_{A}$;
d) $\frac{1}{2}\theta_{A}$;
e) $\frac{2}{5}\theta_{A}$.
17. O coeficiente de dilatação linear médio de um certo material é $\alpha = 50\times{10}^{-6}/^{0}C$ e a sua massa específica a $0 ^{0}C$ é $\rho_{0}$. Calcule de quantos por cento varia (cresce ou decresce) a massa específica desse material quando um bloco é levado de $0^{0}C$ a $300^{0}C$.
Se ficarem dúvidas, ou surgirem dúvidas sobre o assunto ao resolver outras séries de exercícios de outra origem, não faça cerimônia. Pergunte por meio de um dos canais abaixo.
Curitiba, 19 de maio de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
