Física – Movimentos ondulatórios
Estes movimentos podem ser de duas naturezas. Podem ser eletromagnéticas, como é o caso da luz e um amplo espectro de frequências acima e abaixo da faixa visível. Também podem ser mecânicas, como é o caso das ondas sonoras e outros tipos de ondulações.
Neste capítulo abordaremos as ondulações mecânicas, que dependem de um meio material para se propagar. As partículas do meio material oscilam em torno de sua posição de equilíbrio. As oscilações podem acontecer de duas formas. Transversais, quando a onda se propaga em uma direção e as partículas oscilam numa direção perpendicular à de propagação. Longitudinais são aquelas em que as partículas oscilam na mesma direção em que a onda se propaga. Isso faz com que ocorram regiões de compressão e regiões de rarefação. A compressão corresponde aos pontos das cristas e a rarefação equivalem aos denominados vales ou depressões das ondas transversais.
Ondas transversais.
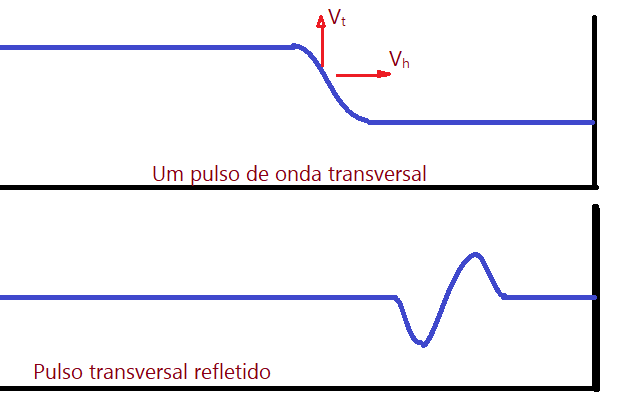
Fixando uma corda num ponto e agitando a outra extremidade, num movimento de subir e descer, provocamos um pulso que se propaga ao longo da corda. Ao atingir a extremidade fixa o pulso sofre inversão de fase e retorna para a outra extremidade, percorrendo toda extensão da corda.
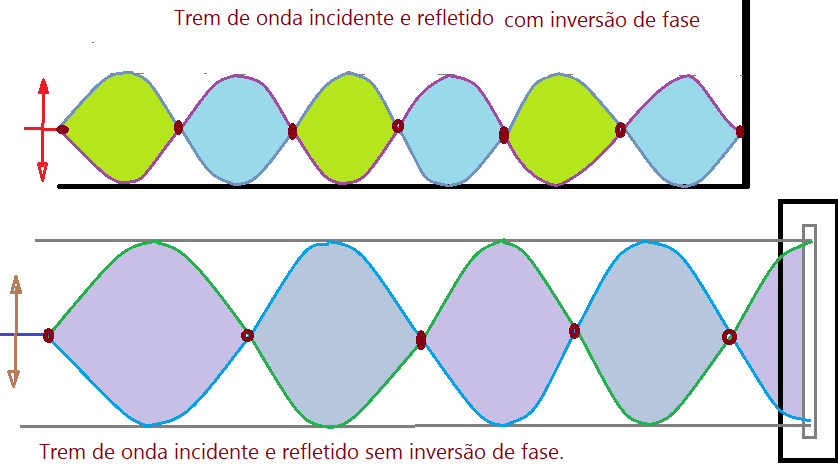
A onda contínua em uma corda fixa, reflete e volta com fase invertida, formando, na extremidade fixa, um ponto imóvel ou um nó. As ondas incidentes e as refletidas interferem, formando os ventres e os nós ao longo do comprimento da corda. Nó, as partículas ficam imóveis em sua posição de equilíbrio. Nos ventres as partículas oscilam com amplitude máxima. Isso ocorre por conta do que denominamos interferência. As amplitudes das duas ondas, a incidente e refletida, se somam. Quando os sentidos coincidem, resulta uma amplitude maior, formando os ventres. Quando os sentidos de oscilação são opostos, a amplitude resultante é muito pequena ou mesmo nula, formando os nós.
Se a corda tem uma extremidade livre, podendo se mover em uma fenda ou suporte móvel, ela reflete sem inversão de fase. Na extremidade livre forma-se um ventre e depois alternam-se nós e ventres. A distância entre dois nós ou dois ventres é igual a um número inteiro de meios comprimentos de onda $x = \frac{\lambda}{2}$.
Essas ondas são denominadas ondas estacionárias. Para cada corda, com um comprimento determinado, haverá fárias frequências que formam ondas estacionárias. Observando nas duas figuras acima, observamos que :
a) Na corda fixa encontramos um número inteiro, par de ventres e um número ímpar de nós. Cada par de ventres corresponde a dois meios comprimentos de onda ou seja um comprimento de onda.
b) Na corda com uma extremidade livre, encontramos cinco ventres e cinco nós. As distâncias entre eles também correspondem a $\frac{\lambda}{2}$. Apenas na extremidade livre temos um ventre que corresponde a $\frac{\lambda}{4}$.

Fontes sonoras
Denominamos fonte sonora qualquer corpo que seja capaz de vibrar com uma ou mais frequências ao ser tangido. Essa vibração se comunica ao ar circundante e se transmite em todas as direções. Instrumentos de sopro tem na embocadura uma palheta ou um tubo flexível que faz o ar vibrar. Uma corda num instrumento é tangida pelo dedo ou uma palheta e começa a vibrar, placas metálicas são percutidas e vibram. Um diapasão, formado por uma haste metálica em formato de $Y$ aproximadamente pode vibrar. Foi e ainda é usado para iniciar a afinação de um instrumento de cordas, uma vez que sempre irá produzir a mesma frequência. Também os regentes de corais, para dar o tom correto aos integrantes usa frequentemente um instrumento desse tipo. Veja a figura a seguir:
Ressonância
Todos os corpos, sejam eles sólidos, líquidos ou gasosos têm uma ou mais de uma frequências naturais de vibração. Neste caso, ao serem atingidos pelas vibrações de uma onda qualquer, podem entrar em vibração, pelo fenômeno do que chamamos de ressonância. Copos de cristal podem quebrar-se ao serem atingidos pelas notas mais agudas de determinados cantores, especialmente os líricos. Sua voz atinge alturas suficientes para colocar em vibração as partículas do cristal. A ressonância pode provocar a quebra pois a amplitude de vibração ultrapassa um limite, que rompe a coesão das moléculas.
Em cordas tracionadas, tubos cheios de uma substância gasosa, placas metálicas, hastes, podem entrar em ressonância, emitindo um conjunto de sons harmônicos, cujas frequências são múltiplas da fundamental.
O mesmo acontece com cordas tracionadas como num instrumento musical e ainda produzem a ressonância do som resultante dentro da “caixa” do instrumento.
Uma onda sonora estacionária em um tubo de Kundt, aberto nas duas extremidades, forma um ventre em cada extremidade e um número $n$ de ventres intermediários. O som fundamental é o que forma apenas um ventre em cada extremidade, tendo um nó no ponto médio. O comprimento de onda dessa onda que correspondente ao som fundamental ou “primeiro harmônico”, é igual ao dobro do comprimento do tubo. Quando houver a formação de dois ventres nas extremidades e mais um no meio, teremos o som denominado de “segundo harmônico” do som fundamental. Na medida que o número de ventres for aumentando, o número do harmônico também cresce. O tubo aberto é capaz de reproduzir todos os sons harmônicos do fundamental.
Tubo de Kundt (tubo aberto)
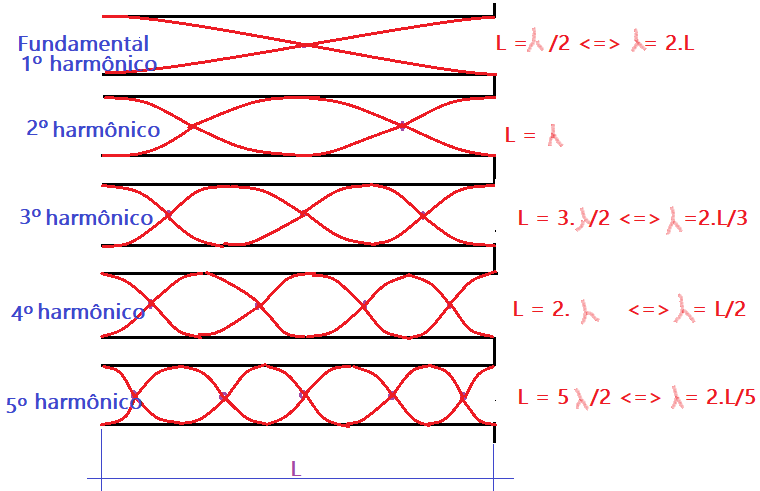
No som fundamental ou primeiro harmônico, temos que $\color{Blue}{\lambda = 2\times L}$ e como a velocidade do som no ar é constante temos que:
$ v = \lambda\times f = {2\cdot L\times f}$
Fundamental ou Primeiro harmônico: $\lambda_{1} = 2\times L$$\Leftrightarrow$$f_{1} = \frac{v}{\lambda_{1}}$
$$\color{Blue}{f_{1} = \frac{v}{2\times L}}$$
Segundo harmônico: $\lambda_{2} = \frac{2L}{2} = L$$\Leftrightarrow$$f_{2}=\frac{2v}{2L}$
$$\color{Blue}{f_{2} = \frac{v}{L}}$$
Terceiro harmônico: $\lambda_{3}= \frac{2L}{3}$$\Leftrightarrow$$f_{3}=\left(\frac{v}{\frac{2L}{3}}\right)$
$$\color{Blue}{f_{3}= \frac{3v}{2L}}$$
Quarto harmônico: $\lambda_{4}=\frac{2L}{4}$$\Leftrightarrow$$f_{4}=\left(\frac{v}{\frac{2L}{4}}\right)$
$$\color{Blue}{f_{4}=\frac{2v}{L}}$$
Quinto harmônico: $\lambda_{5}=\frac{2L}{5}$$\Leftrightarrow$$f_{5}=\left(\frac{v}{\frac{2L}{5}}\right)$
$$\color{Blue}{f_{5} = \frac{5v}{2L}}$$
Expressões genéricas de $\lambda$ e $f$:
$$\color{Brown}{\lambda_{n}= \frac{2L}{n}}$$
$$\color{Brown}{f_{n} = \frac{n\times v}{2\cdot L}}$$
Ressonância em tubo fechado.
No tubo fechado, a extremidade fechada funciona como na corda fixa a extremidade fixa. Ali se forma um nó. No som fundamental ou primeiro harmônico, o comprimento do tubo é igual a $L =\frac{\lambda}{4}$. O próximo harmônico será $L=\frac{3\lambda}{4}$ e portanto será o terceiro harmônico. Se continuarmos, encontraremos sempre um número ímpar de $\frac{\lambda}{4}$, ou seja só teremos os harmônicos ímpares. Vejamos a figura a seguir.
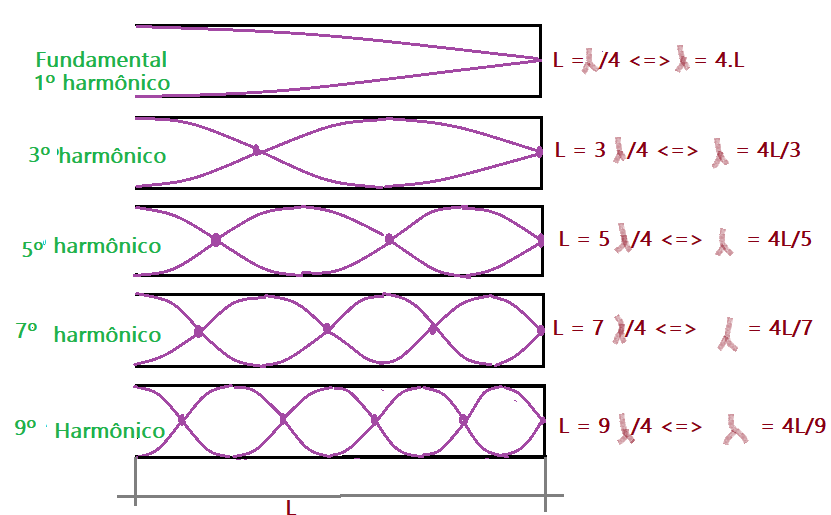
A velocidade do som é a mesma pois o meio de propagação é o ar. Portante aqui teremos:
$ v = \lambda\cdot f $$\Leftrightarrow$$ v = 4\times L\cdot f$
Primeiro harmônico: $\lambda_{1}= 4\times L$$\Leftrightarrow$$f_{1}=\frac{v}{4L}$
$$\color{Blue}{f_{1}=\left(\frac{v}{4L}\right)}$$
Terceiro harmônico: $\lambda_{3}= \frac{4L}{3}$$\Leftrightarrow$$f_{3}=\left(\frac{v}{\frac{4L}{3}}\right)$
$$\color{Blue}{f_{3}=\left(\frac{3v}{4L}\right)}$$
Quinto harmônico: $\lambda_{5}=\frac{4L}{5}$$\Leftrightarrow$$f_{5}=\left(\frac{v}{\frac{4L}{5}}\right)$
$$\color{Blue}{f_{5}=\left(\frac{5v}{4L}\right)}$$
Sétimo harmônico: $\lambda_{7}=\frac{4L}{7}$$\Leftrightarrow$$f_{7}=\left(\frac{v}{\frac{4L}{7}}\right)$
$$\color{Blue}{f_{7}=\left(\frac{7v}{4L}\right)}$$
Expressões genéricas para harmônicos de ordem $n#.
$$\color{Brown}{\lambda_{n}=\frac{4L}{n}}$$
$$\color{Brown}{f_{n}= \frac{nV}{4L}}$$
Ondas estacionárias em cordas fixas e tracionadas.
Todos nós já observamos um instrumento de cordas como violão, cavaquinho, violino, violoncelo, viola, banjo, piano e outros. Os sons são produzidos ao tangermos as diversas cordas, fazendo-as vibrar. Há que levar em conta a espessura da corda, o material de que é feita e a tração aplicada. As vibrações da corda são comunicadas ao ar circundante e uma caixa ressonante se encarrega de ampliar a intensidade, bem como compor o timbre do instrumento. A caixa de ressonância deve ser feita de madeira adequada, para obtenção de uma sonoridade mais rica e agradável. Também a forma da caixa influencia nesse pormenor.
É fácil perceber que a corda, para poder sofrer tração, precisa ser fixada em ambas as extremidades, o que resulta na formação de um nó em cada extremidade. Entre esses nós formam-se um número inteiro de ventres ou seja meios comprimentos de onda.
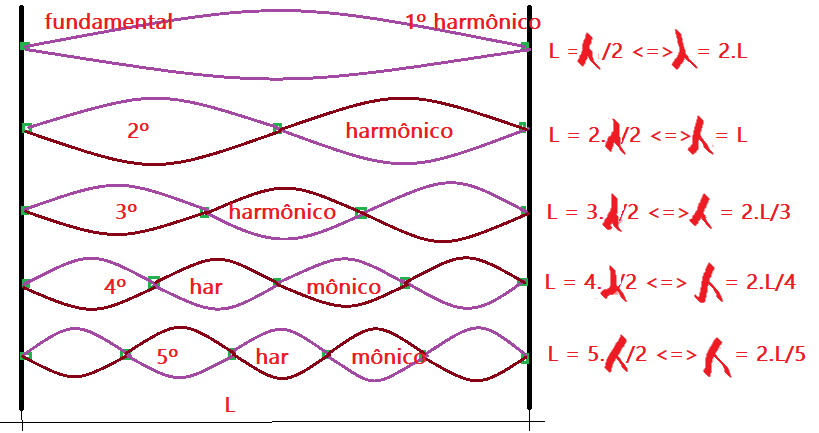
A velocidade será pois: $v = \lambda\cdot f$$\Leftrightarrow$$v = 2\times L\times f$
Primeiro harmônico: $\lambda_{1}= 2\times L$$\Leftrightarrow$
$$\color{Blue}{f_{1}=\frac{v}{2L}}$$
Segundo harmônico: $\lambda_{2}= \frac{2v}{2L}$$\Leftrightarrow$$f_{2}=\frac{v}{L}$
$$\color{Blue}{f_{2}=\frac{v}{L}}$$
Terceiro harmônico: $\lambda_{3}=\frac{2L}{3}$$\Leftrightarrow$$f_{3}= \left(\frac{v}{\frac{2L}{3}}\right)$
$$\color{Blue}{f_{3}=\frac{3v}{2L}}$$
Quarto harmônico: $\lambda_{4}=\frac{2L}{4}$$\Leftrightarrow$$f_{4}=\left(\frac{v}{\frac{2L}{4}}\right)$
$$\color{Blue}{f_{4}=\frac{2v}{L}}$$
Quinto harmônico: $\lambda_{5}=\frac{2L}{5}$$\Leftrightarrow$$f_{5}=\left(\frac{v}{\frac{2L}{5}}\right)$
$$\color{Blue}{f_{5}= \frac{5v}{2L}}$$
Expressões genéricas:
$$\color{Brown}{\lambda_{n}= \frac{2L}{n}}$$
$$\color{Brown}{f_{n}=\frac{nv}{2L}}$$
Nota: A sequência de formação dos harmônicos em tubo aberto e corda fixa é idêntica. Não podemos fazer ressoar uma corda livre pois ela não precisaria ser tracionada, o que só é factível sendo as extremidades fixas.
Vamos por em prática o que foi visto
01. Em um tubo sonoro fechado de comprimento igual a 0,5 m, forma-se um harmônico de frequência igual a 850 Hz. Sendo a velocidade do som no interior do tubo igual a 340 m/s, qual é o harmônico formado nesse tubo?
$\color{Blue}{L = 0,5\, m}$
$\color{Blue}{f = 850\,Hz}$
$\color{Blue}{v = 340,0\,m/s}$
$$\color{Blue}{f_{n}= \frac{nv}{4L}}$$
$ 850 = \frac{n\times 340}{4\times{0,50}}$$\Leftrightarrow$${850,0}\times{8,0} = 340\times n$
$\frac{1700}{340} = n$$\Leftrightarrow$$n = 5$
$$\color{Brown}{n = 5}$$
02. (UFJF-MG) Considerando que a velocidade do som no ar é igual a 340 m/s e que o canal auditivo humano pode ser comparado a um tubo de órgão com uma extremidade aberta e a outra fechada, qual deveria ser o comprimento do canal auditivo para que a frequência fundamental de uma onda sonora estacionária nele produzida seja de $3400\,Hz$?
$\color{Blue}{f_{1} = 3400\,Hz}$
$\color{Blue}{v = 340,0\,m/s}$
$\color{Blue}{n = 1}$
$\color{Blue}{f_{n}= \frac{n\times V}{4\times L}}$
$ 3400 = \frac{1\times {340}}{4\times L}$$\Leftrightarrow$${4,0}\times L = \frac{340}{3400}$
$L = \frac{1}{4\times 10} = 0,025\, m$
$$\color{Brown}{L = 0,025\, m}$$
03. (Udesc)-Dois tubos sonoros de um órgão têm o mesmo comprimento, um deles é aberto e o outro fechado. O tubo fechado emite o som fundamental de $500\,Hz$ na temperatura de$\theta = 20^0C$ e na pressão atmosférica. Entre as frequências a seguir, indique a que esse tubo não é capaz de emitir.
a) 1500\,Hz;
b) 4500\,Hz;
c) 1000\,Hz;
d) 2500\,Hz;
e) 3500\,Hz.
$f_{1}= \frac{1\cdot v}{4\times L}$$\Leftrightarrow$$ 500 = \frac{340}{4\times L}$
$4,0 \times L = \frac{340}{500}$$\Leftrightarrow$$ L = \frac{340}{2000} = 0, 17 m$
$1000= \frac{n\times 340}{4\times 0,17}$$\Leftrightarrow$$ n = \frac{1000\times 0,68}{340}= \frac{680}{340} = 2$
Este som não pode ser emitido, pois os tubos fechados emitem apenas os sons harmônicos ímpares. Sendo par, não é possível essa ressonância. Portanto o único som impossível nesse tubo é a letra (c).
04. Um pulso ondulatório senoidal é produzido em uma extremidade de uma corda longa e se propaga por toda a sua extensão. A onda possui uma frequência de 50\,Hz e comprimento de onda 0,5\, m. Em quanto tempo a onda percorre uma distância de 10\,m na corda?
$\color{Blue}{f = 50,0\,Hz}$
$\color{Blue}{\lambda = 0,5\,m}$
$\color{Blue}{x = 10\, m}$
$v =\lambda\times f = 0,5\times 50 = 25\,m/s$
$x = v\times t$$\Leftrightarrow$$ t = \frac{10}{25} = 0,4\,s$
05. Um tubo cheio de ar, aberto em suas extremidades, é aproximado de um alto-falante, que por sua vez está ligado a um gerador de audiofrequências. Sendo o comprimento do tubo igual a $\color{Blue}{L=1,36\, m}$, a velocidade do ar no ambiente igual $\color{Blue}{v= 340,0\, m/s}$, determine a frequência do som fundamental e dos três harmônicos ímpares que seguem.
$\color{Blue}{L=1,36\,m}$
$\color{Blue}{v = 340,0\,m/s}$
$\color{Blue}{f_{n} = \frac{n\times v}{2L}}$
$f_{n}= \frac{1\times340,0}{2\times 1,36}$$\Leftrightarrow$$f_{1} = \frac{340}{2,72}= 125\, Hz$
$$\color{Brown}{f_{1} = 125,0\,Hz}$$
$f_{3}= \frac{3\cdot 340}{2\times {1,36}}$$\Leftrightarrow$$f_{2} =\frac{1020}{2,72}= 375,0\,Hz$
$$\color{Brown}{f_{3} = 375,0\,Hz}$$
$f_{5}=\frac{5\times 340}{2\times 1,36} = \frac{1700}{2,72}$
$$\color{Brown}{f_{5}=625,0\,Hz}$$
$f_{7}=\frac{7\times 340}{2\times 1,36}$$\Leftrightarrow$$f_{7}= \frac{2380}{2,72} = 875,0\,Hz$
$$\color{Brown}{f_{7}=875,0\,Hz}$$
06. Um tubo de vidro transparente, tem diâmetro de $\color{Blue}{5\,cm}$ está cheio de água e sua base está ligada por um conduto, provido de registro tipo (aberto/fechado), por onde a água escoa lentamente para um reservatório disposto em nível inferior. Dispondo de um diapasão cuja frequência fundamental é $\color{Blue}{f = 510\,Hz}$, abre-se o registro e em seguida percute-se o diapasão, aproximando-o da boca do tubo. O som irá ressoar pela primeira vez quando a altura da coluna de ar no tubo alcançar que valor? E a segunda ressonância, correspondente ao terceiro harmônico, irá ocorrer com qual altura?
Temos a frequência sempre igual a $\color{Green}{f = 510\,Hz}$. A velocidade do som no ar ambiente é considerada $\color{Green}{v= 340,0\, m/s}$. O tubo terá $\color{Green}{L = \frac{\lambda}{4}}$ na primeira ressonância.
$$\color{Blue}{f_{n} = \frac{n\times v}{4\times L_{1}}}$$
$f_{1}= \frac{340\times 1}{4\times L_{1}}$$\Leftrightarrow$$510 = \frac{340}{4\times L}$
$L = \frac{340}{510\times 4}$$\Leftrightarrow$$ L_{1} = \frac{2}{3\times 4}$
$L = \frac{2}{12}$$\Leftrightarrow$$L_{1} = \frac{1}{6} = 0,1666…$
$$\color{Brown}{L_{1} \simeq 0,167\, m}$$
A segunda ressonância irá ocorrer quando o tubo tiver comprimento suficiente para conter $\frac{3\times\lambda}{4}$
$$\color{Blue}{f_{n}=\frac{n\times v}{4\times L}}$$
$f_{3}= \frac{3\cdot 340}{4\times L_{3}}$$\Leftrightarrow$$L_{3} = \frac{3\times 340}{4\times 510}$
$L_{3}= \frac{3\times 2}{4\times 3}$$\Leftrightarrow$$L_{3}=\frac{1}{2}= 0,50 \,m$
$$\color{Brown}{L_{3} = 0,50\,m}$$
07. Considere o mesmo tubo da questão anterior, para um diapasão de $\color{Blue}{f=680\,Hz}$ e outro de $\color{Blue}{f= 850\,Hz}$, determinando os mesmos casos de ressonância.
Os cálculos são feitos da mesma forma que no anterior. Mudam apenas as frequências.
$$\color{Blue}{f_{n}=\frac{n\times v}{4\times L}}$$
$680 = \frac{1\times v}{4\times L_{1}}$$\Leftrightarrow$$L_{1}=\frac{340}{4\cdot 680}$
$L_{1}= \frac{1}{4\times 2} = \frac{1}{8}$$\Leftrightarrow$$L_{1}= 0,125\, m$
$$\color{Brown}{L_{1}=0,125\, m}$$
$$\color{Blue}{f_{3}= \frac{3\times 340}{4\times L}}$$
$L_{3} = \frac{3\times 340}{4\times 680}$$\Leftrightarrow$$L_{3}= \frac{3}{8}= 0,375\,m$
$$\color{Brown}{L_{3}=0,375\,m}$$
Para frequência de $f = 850\,Hz$.
$$f_{n}= \frac{1\times 340}{4\times L_{1}}$$
$850 = \frac{340}{4\times L_{1}}$$\Leftrightarrow$$ L_{1}= \frac{340}{4\times 850}$
$L_{1}=\frac{2}{4\cdot 5}$$\Leftrightarrow$$L_{1}=\frac{1}{10}= 0,10$
$$\color{Brown}{L_{1}=0,10\,Hz}$$
$ f_{3}= \frac{3\times v}{4\times L_{3}}$$\Leftrightarrow$$ 850 = \frac{3\times 340}{4\times L_{3}}$
$L_{3} = \frac{3\times 340}{4\times 850}$$\Leftrightarrow$$ L_{3}=\frac{3\times 2}{4\times 5}= \frac{3}{10}$
$$\color{Brown}{L_{3}= 0,30\,m}$$
Agora é sua vez de por a mão na massa.
01. A tecla mais aguda de um piano corresponde a uma frequência
150 vezes maior que a corda mais grave. Se o comprimento da
corda mais aguda é 5,0 cm, quanto teria que ter a corda mais
grave, se elas tivessem a mesma densidade linear de massa e a
mesma tensão?
02. Uma corda de violino de $L=0,32\,m$ está tocando a nota A(Lá), acima
da nota C(Dó) na escala bem temperada (correspondente a $440\,Hz$).
(a) Qual é o comprimento de onda do harmônico fundamental?
(b) Quais são as frequências e comprimento de onda da onda
sonora produzida? (c) Por que há diferença?
03. Tubos de órgão abertos e fechados: Qual é a freqüência
fundamental e os três primeiros parciais de um tubo de órgão
de $L = 26\,cm$ de comprimento a $\theta = 20^{0}C$, se ele for:
(a) aberto;
(b)fechado?
04. Uma flauta é desenhada para tocar a nota dó central $f =262 Hz$
como frequência fundamental quando todos os buracos estão
tampados. Qual deve ser a distância entre o bocal e o fim da
flauta (obs: essa é apenas uma distância aproximada)? Assuma
a temperatura de $\theta =20^{0}C$.
05. Se a temperatura fosse apenas $10^0C$, qual seria a frequência
da nota tocada do mesmo modo que no problema anterior? Lembre do post anterior que $V = 330,4 + 0,59\theta$
06. (UFMG) Para que um corpo vibre em ressonância com um outro é preciso que:
a) seja feito do mesmo material que o outro;
b) vibre com a maior amplitude possível;
c) tenha uma frequência natural igual a uma das frequências naturais do outro;
d) vibre com a maior frequência possível;
e) vibre com a menor frequência.
07. (UNIP) A Ponte de Tacoma, nos Estados Unidos, ao receber impulsos periódicos do vento, entrou em vibração e foi totalmente destruída. O fenômeno que melhor explica esse fato é:
a) o efeito Doppler
b) a ressonância
c) a interferência
d) a difração
e) a refração
08. Sobre uma corda vibrante de $L= 2\,m$ de comprimento é formada uma onda estacionária correspondente ao primeiro harmônico (frequência fundamental). O comprimento de onda dessa oscilação tem módulo igual a:
a) 4,0 m;
b) 2,0 m;
c) 1,0 m;
d) 0,5 m;
e) 8,0 m.
09. Uma onda estacionária cujo comprimento de onda mede $\lambda= 50\, cm$ é formada em uma corda vibrante de $L=4,0\,m$ de comprimento. A ordem do harmônico formado é igual a:
a) 8
b) 12
c) 16
d) 4
e) 2
10. (UCS-Adaptado) Um tubo sonoro aberto emite o seu quinto harmônico com frequência de $f= 1,7\,kHz$. A velocidade do som, no ar que preenche o tubo, tem módulo igual a $v= 340\,m/s$. O comprimento do tubo vale:
a) 5,0 m
b) 0,5 m
c) 0,25 m
d) 0,025 m
e) 2,0 m
11. Em uma corda vibrante, forma-se uma onda estacionária correspondente ao quinto harmônico. O número de meio comprimento de onda e o de nós nessa corda equivalem a, respectivamente:
a) 4 e 5
b) 5 e 4
c) 6 e 5
d) 5 e 6
e) 2 e 3
12. (Enem PPL 2013) Em um violão afinado, quando se toca a corda Lá com seu comprimento efetivo (harmônico fundamental), o som produzido tem frequência de 440 Hz.
Se a mesma corda do violão é comprimida na metade do seu comprimento, a frequência do novo harmônico:
a) Se reduz à metade, porque o comprimento de onda dobrou;
b) Dobra, porque o comprimento de onda foi reduzido à metade;
c) Quadruplica, porque o comprimento de onda foi reduzido à metade;
d) Quadruplica, porque o comprimento de onda foi reduzido à quarta parte;
e) Não se modifica, porque é uma característica independente do comprimento da corda que vibra.
13. (Enem simulado 2009) -Um dos modelos usados na caracterização dos sons ouvidos pelo ser humano baseia-se na hipótese de que ele funciona como um tubo ressonante. Neste caso, os sons externos produzem uma variação de pressão do ar no interior do canal auditivo, fazendo a membrana (tímpano) vibrar. Esse modelo pressupõe que o sistema funciona de forma equivalente à propagação de ondas sonoras em tubos com uma das extremidades fechadas pelo tímpano. As frequências que apresentam ressonância com o canal auditivo têm sua intensidade reforçada, enquanto outras podem ter sua intensidade atenuada.

Tímpano e canal auditivo (Foto: Google Imagens)
Considere que, no caso de ressonância, ocorra um nó sobre o tímpano e ocorra um ventre da onda na saída do canal auditivo, de comprimento L igual a 3,4 cm. Assumindo que a velocidade do som no ar (v) é igual a 340 m/s, a frequência do primeiro harmônico (frequência fundamental, n = 1) que se formaria no canal, ou seja, a frequência mais baixa que seria reforçada por uma ressonância no canal auditivo, usando este modelo é:
a) 0,025 kHz, valor que considera a frequência do primeiro harmônico como igual a nv/4L e equipara o ouvido a um tubo com ambas as extremidades abertas;
b) 2,5 kHz, valor que considera a frequência do primeiro harmônico como igual a nv/4L e equipara o ouvido a um tubo com uma extremidade fechada;
c) 10 kHz, valor que considera a frequência do primeiro harmônico como igual a nv/L e equipara o ouvido a um tubo com ambas as extremidades fechadas;
d) 2.500 kHz, valor que expressa a frequência do primeiro harmônico como igual a nv/L, aplicável ao ouvido humano;
e) 10.000 kHz, valor que expressa a frequência do primeiro harmônico como igual a nv/L, aplicável ao ouvido e a um tubo aberto e fechado.
14. (Enem 2016) Um experimento para comprovar a natureza ondulatória da radiação de micro-ondas foi realizado da seguinte forma: anotou-se a frequência de operação de um forno de micro-ondas e, em seguida, retirou-se sua plataforma giratória. No seu lugar, colocou-se uma travessa refratária com uma camada grossa de manteiga. Depois disso, o forno foi ligado por alguns segundos. Ao se retirar a travessa refratária do forno, observou-se que havia três pontos de manteiga derretida alinhados sobre toda a travessa. Parte da onda estacionária gerada no interior do forno é ilustrada na figura.

Foto: Google Imagens
De acordo com a figura, que posições correspondem a dois pontos consecutivos da manteiga derretida?
a) I e III;
b) I e V;
c) II e III;
d) II e IV;
e) II e V .
Estude, resolva os exercícios e se tiver dúvidas, já sabe o que fazer. Fale comigo por um dos canais abaixo listados.
Curitiba, 17 de maio de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
