Física – Sistema de forças binários.

Um sistema binário é um sistema de duas forças, de mesma direção, sentidos opostos e módulos iguais. Podemos observar o que acontece com as nossas mãos durante o ato de dirigir um automóvel, uma bicicleta, uma motocicleta. Manejar controles giratórios, manoplas de torneiras, usar saca-rolhas e outros dispositivos. Para abrir ou fechar a tampa de vidros de medicamentos, conservas e outros conteúdos, usamos os dedos formando um sistema binário.



Efeito de um binário
Pelos exemplos citados, podemos notar que o efeito da aplicação de um binário é produzir rotação. Não produz como efeito primário movimento de deslocamento em linha reta ou curva. Isso se deve ao fato de ser um sistema cuja resultante é nula. Sendo a resultante nula, o corpo se mantem em equilíbrio estático. Os sistemas de freios dos veículos habitualmente funcionam na forma de binários, aplicados nas rodas ou em um ponto delas.
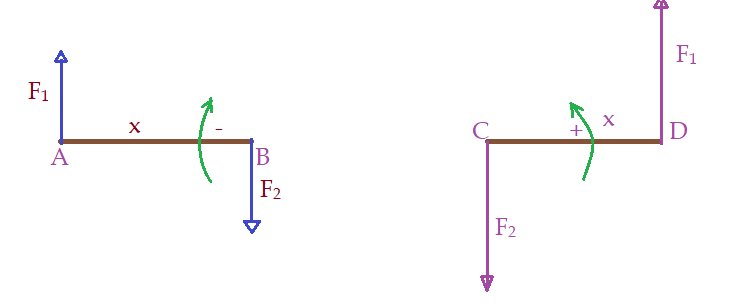
Temos na figura um par de sistemas binários, onde o primeiro é de sentido horário (-) e o segundo anti-horário(+).
O segmento entre as forças é o braço do binário. Este braço pode eventualmente não ser o próprio segmento, se as forças forem oblíquas em relação a ele. Vejamos os exemplos.
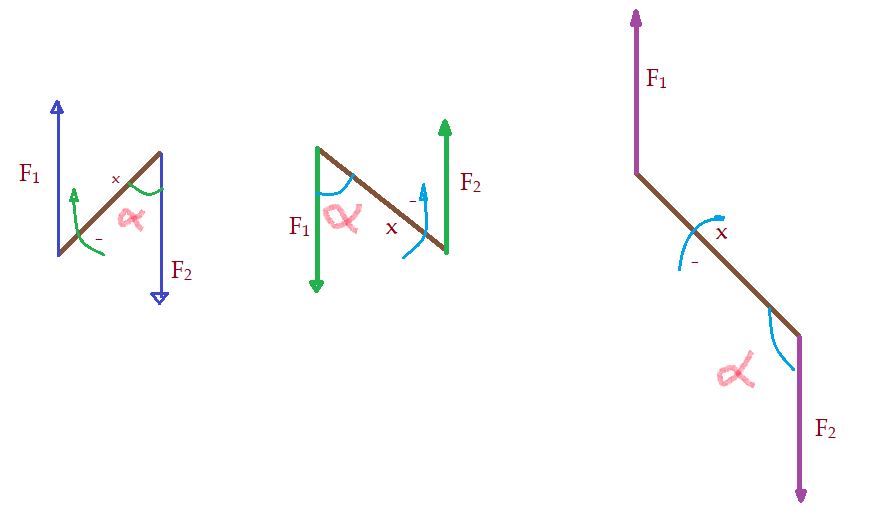
O braço pode ser calculado pelo produto do segmento pelo $sen\alpha$ entre o mesmo e as forças.
Colocando o sistema em um plano cartesiano, vemos que a resultante será nulo. Pode-se perguntar como é produzido o movimento de rotação?
A resposta é simples. O fato da resultante ser nula não implica na nulidade do Momento Estático do sistema.
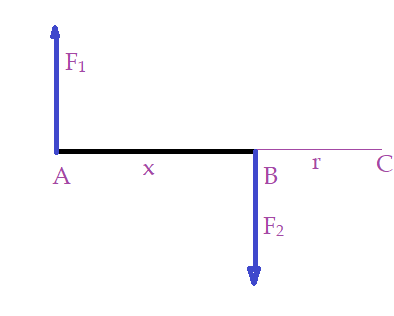
Tomando um ponto C, fora do braço do binário, teremos:
$M_{C}F_{1} + M_{C}F_{2}\cdot r = M_{C}$
$-F_{C}\cdot {x+ r} + F_{2}\cdot r = M_{C}$
Os módulos das duas forças são iguais: $ \overline{F_{1}} = \overline{F_{2}} = \bar{F}$
$ -F\cdot x -F\cdot r + F\cdot r = M_{C}$
$M_{C} = -F\cdot x$
O sinal (-) neste caso indica que o sentido de rotação provocado por esse binário é horário. Generalizando podemos então usar:
$$\color{Brown}{M_{o} = F\cdot x }$$
Em qualquer problema onde ocorra a intervenção de mais de um binário, iremos analisar os sentidos (sinais) em função da rotação que eles provocam. Os módulos serão sempre obtidos multiplicando o módulo das forças pelo braço do binário.
No caso de as forças serem inclinadas em relação ao segmento que une seus pontos de aplicação, multiplicaremos pelo seno do ângulo formado.
$$\color{Blue}{M_{o} = F\cdot x\cdot sen\alpha}$$
Vejamos exemplos de binários com sentidos opostos e ângulos diversos.
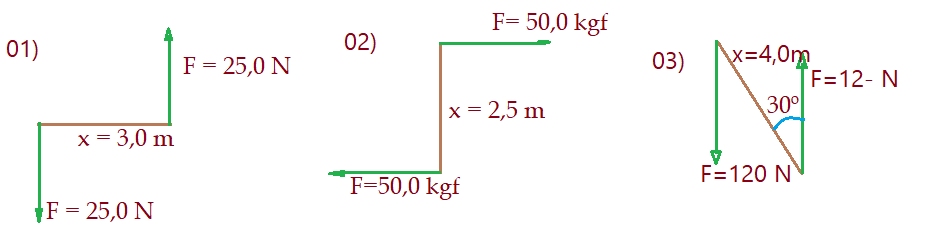
No primeiro caso, notamos que o sentido das forças produz rotação anti-horária e portante o momento será (+).
$\color{Blue}{M_{o} = F\cdot x}$
$M_{o} = {25,0}\cdot {3,0} = 75,0\, Nm$
No segundo caso observamos que o sentido do binário é de rotação horária e por isso o momento será (-).
$M_{o} = – F\cdot x $
$M_{o} = – {50,0}\cdot {2,5} = -125,0 kgm$
No terceiro encontramos forças em sentido anti-horário e formando com o segmento que une seus pontos de aplicação um ângulo $\alpha = 30^{0}$. Isso nos dá momento (+) e usaremos a fórmula com a multiplicação pelo seno desse ângulo.
$M_{o} = F\cdot x\cdot sen\alpha$
$M_{o} = {120,0}\cdot {4,0}\cdot sen{30^{0}}$
$M_{o} = 480,0\cdot {\frac{1}{2}} = 240,0 Nm$
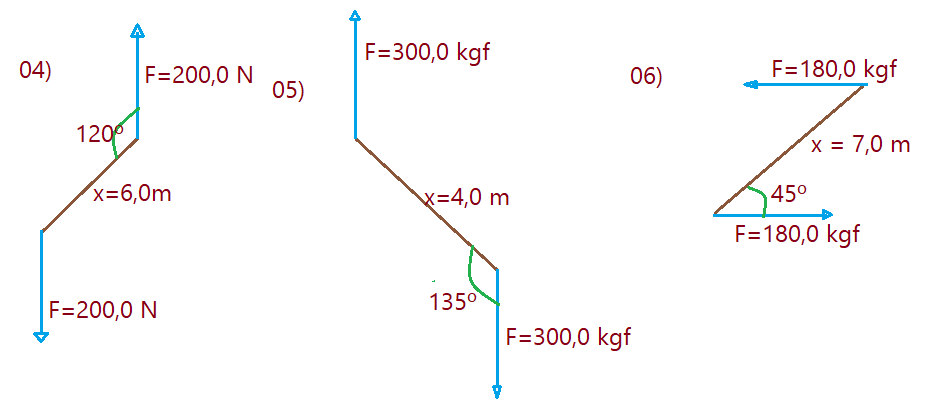
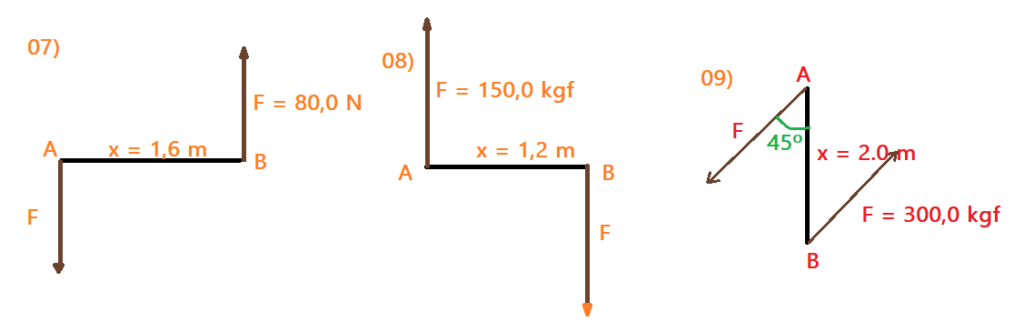
Hora de se virar um pouco.
Determine o momento e seu sentido de rotação para os binários abaixo.
Binários simétricos
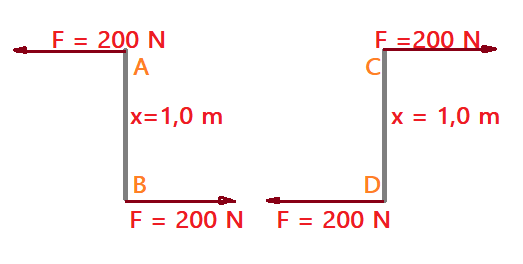
Denominamos $\color{Brown}{Binários simétricos}$ aos binários que apresentam braços iguais, porém as forças são diretamente opostas umas às outras.
Vejamos na figura ao lado.
Binários equivalentes
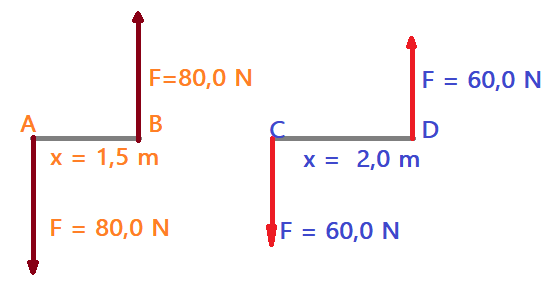
Denominamos $\color{Brown}{Binários equivalentes}$ aos binários que têm o mesmo momento resultante, porém suas forças e braços tem medidas diferentes. É fácil notar que os braços maiores, permitem o uso de forças de menor intensidade, para produzir o mesmo efeito.
Se ficarem dúvidas, peça ajuda pelos canais listados abaixo.
Curitiba, 26 de março de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
