FI.ME.018-01. Física – Mecânica. Hidráulica – Hidrodinâmica.
Efeito da aceleração sobre o líquido.
Um recipiente contendo um líquido em repouso, apresenta a superfície livre na posição horizontal. Veja a figura.
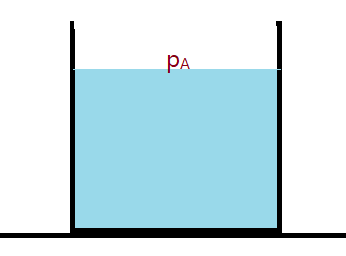
Se o recipiente sofrer uma aceleração, a superfície livre do líquido ficará inclinada, elevando-se no sentido oposto ao da aceleração. Se analisarmos uma partícula do líquido localizada na superfície do mesmo, ela sofrerá a ação de duas forças. O peso $P=m\times g$ e uma força $F$, normal à superfície livre e resultante da ação das demais partículas da massa sobre essa que estamos tomando isoladamente.
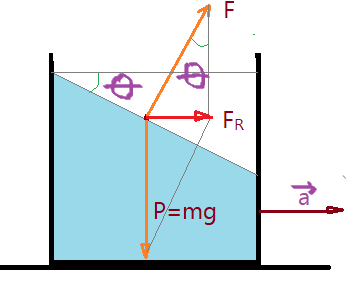
Observamos que o ângulo de inclinação da superfície livre está associado com as forças que atuam sobre cada partícula dessa superfície do líquido.
$F_{R}= m\times a$
$tg\theta = \frac{\not{m}\times a}{\not{m}\times g}$
$$\color{Navy}{a = g\times tg\theta}$$
Isso nos mostra que a inclinação da superfície livre é tanto maior quando maior for o valor da aceleração a que o fluido estiver submetido.
Aceleração centrípeta
Se colocarmos um recipiente circular em movimento de rotação. Poderemos ter MCU ou MCUV. Vejamos o MCU em primeiro lugar. Com determinada velocidade angular, a elevação da superfície é proporcional à aceleração centrípeta que as partículas sofrem.
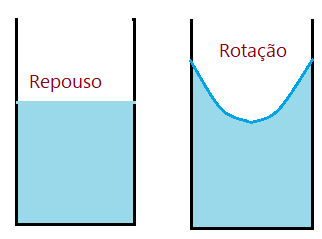
Se houver aceleração angular, a elevação aumenta na proporção que a velocidade angular cresce. Do mesmo modo, havendo desaceleração, a elevação decresce, até atingir o repouso quando a superfície se torna horizontal.
Fluxo de escoamento.
Na hidrostática aprendemos a resolver questões de pressão para os fluidos em equilíbrio, repouso. Agora na hidrodinâmica nos preocuparemos com os fluidos em movimento. Ainda há detalhes desses fenômenos a ser desvendados e os cálculos aí aplicados são de nível superior. Podemos no entanto analisar as situações mais simples e para isso usaremos dois conceitos que nos auxiliarão grandemente.
O escoamento de um fluido forma o que denominamos fluxo. O fluxo pode ser de dois tipos. O fluxo laminar e o fluxo turbulento.
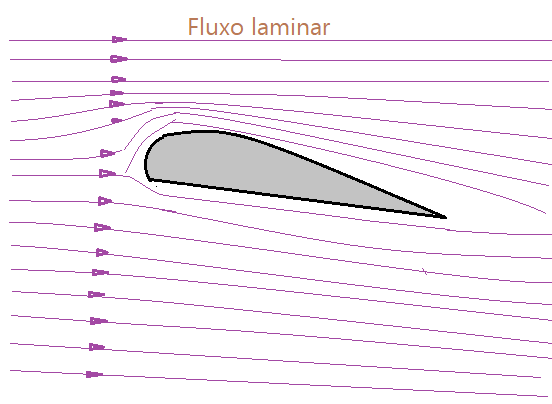
Fluxo laminar: – o fluxo é denominado laminar quando as partículas do fluido se movimentam em linha reta e trajetórias paralelas. Isso é típico de uma canalização em que a velocidade é baixa e não há pontos que provoquem turbulência ou que esta seja mínima. Veja a figura.
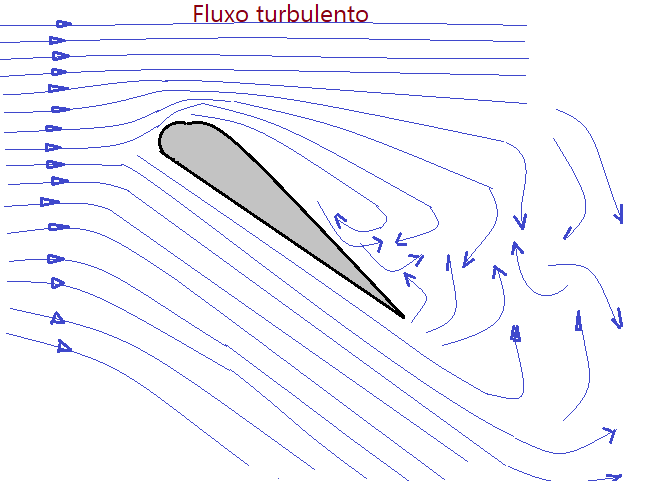
Fluxo turbulento: – o fluxo turbulento ocorre quando há velocidade de escoamento mais elevada e estão presentes pontos causadores de turbulência acentuada. Como mostra a figura.
Linha de corrente é a representação das trajetórias das partículas do fluido durante o escoamento.
Vazão em um ponto
Tomemos um líquido escoando uniformemente por um tubo cilíndrico com velocidade constante.
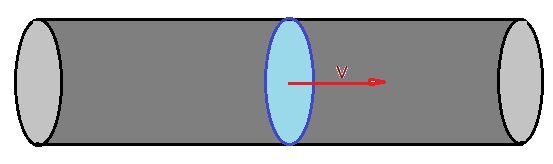
Sendo a velocidade constante um disco imaginário de partículas do líquido, desloca-se de uma distância $\Delta X$ num intervalo de tempo $\Delta t$, o que equivale ao deslocamento de um volume:
$\Delta V = S\times \Delta X$$\Leftrightarrow$$\Delta V = S\times v\times \Delta t$
A vazão será:
$$\color{Maroon}{\phi = \frac{\Delta V}{\Delta t}}$$
Unidades de vazão:$ m^{3}/s$, $cm^{3}/s$, $ l/s$
Exemplo 1. Um líquido escoa com velocidade constante através de um tubo de secção uniforme. Se o fluxo é de $\Delta V= 720\,L$ por minuto. Determine a vazão em $m^3/s$.
$\phi = \frac{720}{\Delta t}$$\Leftrightarrow$$\phi = \frac{720}{60} = 12,0\,L/s$
Sabemos que $1\,L = {10}^{3}cm^3$
$12\,L = 12\times{10}^{3}\,cm^{3}$
$\phi = 12\times{10}^{3}\times {10}^{-3}$$\Leftrightarrow$$\phi = 1,2\times{10}^{-2}\,m^3/s$
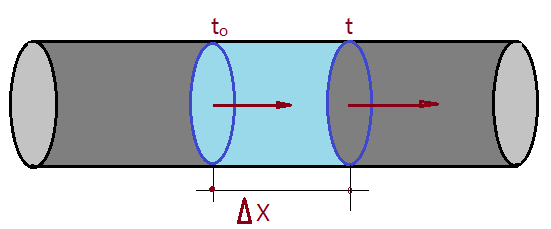
O líquido com velocidade constante percorre uma distância $\Delta X$ em um intervalo de tempo $\Delta t$.
$\Delta X = v\times \Delta t$
O volume será: $V = S\times v\times \Delta t$
Substituindo na expressão da vazão temos:
$\phi = \frac{S\times v\times \Delta t}{\Delta t}$$\Leftrightarrow$$\phi = S\times v$
Exemplo 2. Se um líquido ideal escoa em um tubo de secção reta $S=4,0\,cm^2$, com velocidade linear $v= 30,0\,cm/s$. Determinar a vazão do líquido nesse tubo.
$\phi = S\times v$$\Leftrightarrow$$\phi = 4,0\times {30,0}$
$$\color{Navy}{\phi = 120,0\,cm^{3}/s}$$
Equação da Continuidade
Na figura temos um tubo retilíneo no qual escoa, a velocidade constante $v_{1}$, um líquido ideal, por uma secção reta de área $S_{1}$. Um trecho cônico une esse tubo a outro de dimensão maior, onde o mesmo líquido escoa com velocidade constante $V_{2}$, através da secção reta de área $S_{2}$.
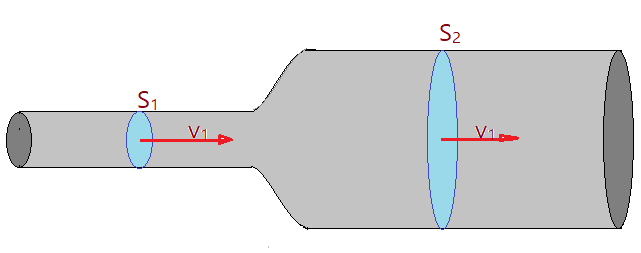
Podemos estabelecer a vazão em cada um dos trechos do tubo. Depois igualaremos as duas expressões, uma vez que o fluxo é uniforme, significando que a vazão é a mesma em todos os pontos do tubo.
$\phi_{1} = S_{1}\times v_{1}$
$\phi_{2}= S_{2}\times v_{2}$
$\phi_{1} = \phi_{2}$$\Leftrightarrow$$ S_{1}\times v_{1} = S_{2}\times v_{2}$
$$\color{Navy}{S_{1}\times v_{1} = S_{2}\times v_{2}}$$
Exemplo 3. Em um tubo escoa um líquido com velocidade $v_{1} = 5,0\,cm/s$ numa secção reta de área $S_{1}= 60,0\,cm^2$ e em outro trecho a secção é de $S_{2}= 15,0\,cm^2$. Determine a velocidade de escoamento nessa parte do tubo.
$$\color{Maroon}{S_{1}\times v_{1} = S_{2}\times v_{2}}$$
${60,0}\times {5,0} = {15,0}\times v_{2}$$\Leftrightarrow$$v_{2} = \frac{60,0\times 5,0}{15,0}$
$$\color{Navy}{v_{2} =20,0\,cm/s}$$
Equação de Bernoulli
Para fluidos ideais ou perfeitos, onde não haja compressão e sem atrito (viscosidade) entre as moléculas, pode-se resolver problemas de escoamento com a equação de Bernoulli.
Imagine um fluxo contínuo num tubo como o da figura que segue:
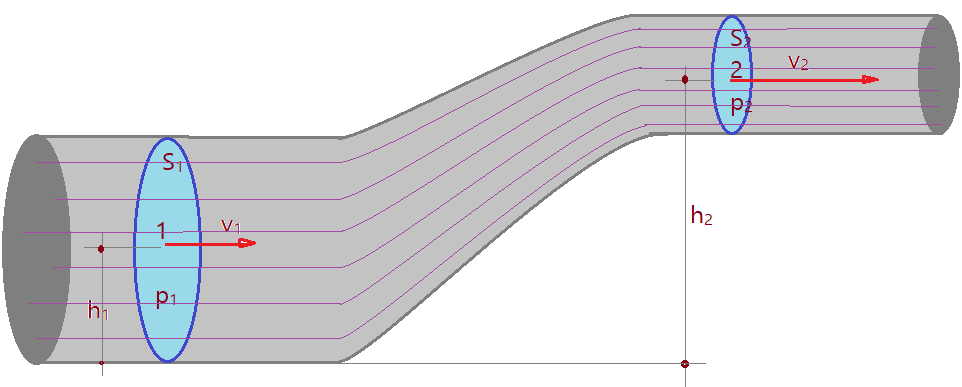
Tomando os pontos $1$ e $2$, onde a secção reta mede $S_{1}$ e $S_{2}$. O fluido escoa com velocidades $v_{1}$ e $v_{2}$, de modo que a vazão é a mesma. A diferença de nível entre os dois pontos nos leva a analisar três estados de energia nesses pontos. A cinética das partículas, a potencial gravitacional e a energia decorrente da pressão do fluido. Isso resulta na equação de Bernoulli.
$$\color{Sepia}{p_{1} + \mu g h_{1} + \frac{\mu {v_{1}}^{2}}{2} = p_{2} + \mu g h_{2} + \frac{\mu {v_{2}}^{2}}{2}= constante}$$
Podemos estabelecer que em fluxo contínuo a expressão para pontos no mesmo nível é:
$h_{1} = h_{2}$$\Leftrightarrow$$p_{1} + \frac{\mu {v_{1}}^{2}}{2} = p_{2} + \frac{\mu {v_{2}}^{2}}{2}$
Por fim temos:
$$\color{Navy}{p + \frac{\mu {v}^{2}}{2} = constante}$$
Equação de Torricelli
Quando estudamos as equações dos movimentos uniformemente variados, usando as equações de Galileu, demonstramos uma equação que relaciona as demais grandezas do movimento, sem uso do tempo. Ela é denominada equação de Torricelli.
$$\color{Maroon}{v^{2} = v_{0}^{2} + 2 a\Delta X}$$
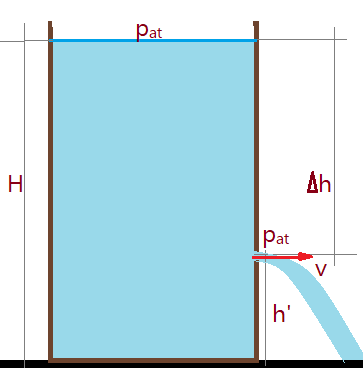
O líquido contido no reservatório atinge a altura inicial $H$. A uma altura $h’$ existe um orifício por onde o líquido escoa a uma velocidade $v$. A diferença de pressão atmosférica entre a superfície livre e o ponto de saída do jato fluido é insignificante.
Enquanto o fluido jorra pelo orifício, o nível da superfície livre desce a uma velocidade muito pequena, podendo ser desprezada, ou seja a velocidade vertical das partículas é $\simeq 0$. Assim a equação de Bernoulli, fica:
$p_{at} + \mu g H + \frac{\mu {v_{v}}^{2}}{2} = p_{at} + \mu g h’ +\frac{\mu {v}^{2}}{2}$
Cancelando os termos simétricos $p_{at}$ e substituindo a velocidade vertical por $0$, teremos:
$\mu g H = \mu g h’ + \frac{\mu {v}^{2}}{2}$
Cancelando o fator comum $\mu$
$g H = g h’ + \frac{{v}^{2}}{2}$$\Leftrightarrow$$2g H = 2g h’ + {v}^{2}$
$2g H – 2g h’ = {v}^{2}$$\Leftrightarrow$$v^{2} = 2g{(H – h’)}$
$$\color{Navy}{v = \sqrt{2g\Delta h}}$$
Se fizermos na equação de Torricelli a velocidade inicial igual à $0$, as duas expressões se equivalem.
$$\color{Brown}{v = \sqrt{2a\Delta X}}$$
Qual será o alcance do jato de líquido que sai do orifício?
Nota-se que é um movimento parabólico. A velocidade de saída é horizontal e na vertical podemos usar a queda livre.
$H-h = \frac{g\times t^{2}}{2}$$\Leftrightarrow$$\frac{2\times{(H-h)}}{g} = t^{2}$
$t = \sqrt{\frac{2\times{(H-h)}}{g}}$
O alcance é dado pela expressão do MU na horizontal.
$ x = v_{x}\times t$$\Leftrightarrow$$ x = \sqrt{2gh}\times\sqrt{\frac{2\times{(H-h)}}{g}}$
$ x = \sqrt{\frac{2gh\times 2\times{(H-h)}}{g}}$$\Leftrightarrow$$ x = \sqrt{4\times h{(H-h)}}$
$$\color{Navy}{x = 2\sqrt{h(H-h)}}$$
Viscosidade
Vamos fazer uma comparação um pouco grosseira, mas que nos ajuda a entender o que é viscosidade. Um caminhão carregado de areia, levanta a sua caçamba, abre a tampa e despeja sua carga num lugar. Qual é a forma que a areia assume?

Pergunto agora. Por qual motivo a areia não cai de modo arrumadinho, formando um cubo ou cilindro? A areia é um líquido? Logicamente que não. Então por que motivo ela não empilha como se fossem pedaços de madeira, uma pilha de tijolos? Os grãos de areia sofrem de atrito entre eles, mas não o suficiente para manter todos juntos num monte bem arrumadinho.
Podemos comparar os grãos de areia às moléculas de um líquido. Essas moléculas, em muito menor escala, também sofrem de “atrito” umas com as outras, ou são atraídas entre si. Isso nos ajuda a perceber por que motivo há líquidos que escoam de modo diferente.
Tomemos por exemplo uma lata de água e uma de mel. Ao inclinar as duas os dois líquidos irão escoar. Qual é a diferença?
A água é praticamente isenta de viscosidade, enquanto o mel é bem mais viscoso e irá escoar mais devagar. Poderíamos dizer que o mel escoa de modo “preguiçoso”. Isso é causado pela viscosidade. Dois derivados do petróleo como a gasolina e o óleo lubrificante de motor ou transmissão. Os dois são hidrocarbonetos, mas as suas viscosidades são bastante diversas.
Vejamos as figuras de escoamento abaixo
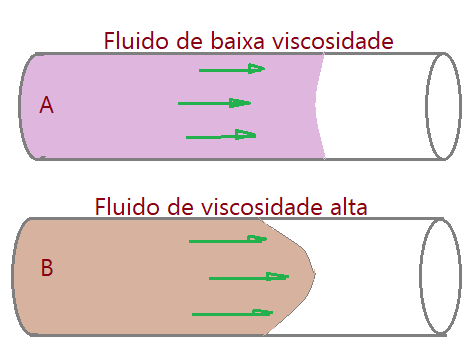
Se ligarmos dois tubos verticais pela sua base a um reservatório de líquidos com densidades diferentes. No líquido de baixa viscosidade a superfície livre que sobe pelo tubo fica aproximadamente horizontal. No líquido viscoso será formado um “menisco” convexo. O atrito das moléculas com as paredes do tubo freia o líquido nas bordas enquanto o centro avança mais rapidamente. Mesmo em fluxo contínuo o líquido escoa mais lentamente nas proximidades das paredes do que pelo centro do tubo.
O atrito entre as moléculas e delas com as paredes do recipiente determina o que se resolveu chamar de perda de carga entre dois pontos. O cálculo minucioso dessas variações implica no uso de conhecimentos matemáticos mais elevados do que é suposto no nível em que estamos.
Chegou o momento dos exercícios
01. Um conduto de 100 mm de diâmetro tem uma vazão de $\phi = 6\,L/s$. Qual a velocidade média de escoamento?
$$\color{Maroon}{\phi = \frac{\Delta V}{\Delta t}}$$
Sendo $\Delta V = S\times v$
$\phi = \frac{\pi D^{2}}{4}\times v$$\Leftrightarrow$$6\times{10}^{3} = \frac{\pi {10}^{2}}{4}\times v$
$v = \frac{6\times 10^{3}\times 4}{\pi 10^{2}} = 7,639 cm/s$
$$\color{Navy}{v\simeq 7,639\,cm/s}$$
02. Calcular o diâmetro de uma canalização para conduzir uma vazão de $\phi =100 L/s$, com velocidade média do líquido em seu interior de $v = 2\,m/s$.
Dados: $2,0\,m/s = 200,0\,cm/s$, $\phi = 100L/s = 10^{5}\,cm^{3}/s$
$$\color{Maroon}{\phi = \frac{\Delta V}{\Delta t} = S\times v}$$
$$\color{Maroon}{S = \frac{\pi D^{2}}{4}}$$
$\phi = \frac{\pi D^{2}}{4}\times v$$\Leftrightarrow$$ 10^{5} = \frac{\pi D^{2}}{4}\times {2,0}\times 10^{2} $
$D^{2} = \frac{10^{5}\times 4}{\pi\times 2\times 10^{2}}$$\Leftrightarrow$$\sqrt{D^{2}}= \sqrt{636,62}\,cm$
$$\color{Navy}{D = 25,23\,cm = 252,3 mm}$$
03. O raio da artéria aorta é cerca de $r_{a}=1,0\, cm$ e o sangue flui através dela com velocidade de $v_{a}= 30,0\,cm/s$.
Calcule a velocidade média do sangue nos capilares dado que cada capilar tem um diâmetro interno de cerca de $D_{c}=8\times 10^{-4}\,cm$ e que existem literalmente bilhões deles, de modo que a área de secção transversal total dos capilares é de cerca de $S_{c}= 2.000\,cm^{2}$.
Dados:$r_{a}=1,0\,cm$, $v_{a}=30,0\,cm/s$ e
$S_{c} = 2000,0\,cm^{2}$
$$\color{Maroon}{S_{1}\times v_{1} = S_{2}\times v_{2}}$$
$\pi {r_{a}}^{2}\times v_{a} = S_{c}\times v_{c}$$\Leftrightarrow$${3,14}\times {30,0} = {2000,0}\times v_{c}$
$v_{c} = \frac{{3,14}\times {30,0}}{2000,0} = 0,0471\,cm/s$
$$\color{Navy}{v_{c} = 0,471\,mm/s}$$
04. Qual deverá ser a área de secção transversal de uma tubulação, em que o ar se move a $V=3,0\,m/s$, de
modo a permitir a renovação do ar, a cada $\Delta t=15\,min$, em um quarto com $V= 300\,m^{3}$ de volume? Admita que a
densidade do ar permaneça constante.
Podemos considerar o quarto como uma continuação da tubulação, por onde o ar irá fluir.
$\Delta t = 15,0\,min = 900,0\,s$
$S\times v = S\times\frac{\Delta X}{\Delta t} = \frac{\Delta V}{\Delta t}$
Então: $S_{1}\times v_{1} = \frac{\Delta V}{\Delta t}$
$S_{1}\times {3,0} = \frac{30,0}{900,0}=\frac{300,0}{900,0\times 3,0}$
$S_{1} = \frac{100,0}{900,0}\simeq 0,11\,m$
$$\color{Navy}{S_{1}\simeq 0,11\,m}$$
05. Água quente circula pela tubulação de um sistema de aquecimento em uma casa. Se a água é bombeada, no térreo, com velocidade de $v_{1}= 0,50\,m/s$ através de um cano com $D_{1}=4,0\,cm$ de diâmetro sob pressão de $p_{1}=3,0\,atm$, determine a velocidade de escoamento e a pressão da água em um cano com $D_{2}=2,6\,cm$ de diâmetro, localizado no andar superior, $h_{2} = 5,0\,m$ acima do térreo.
Considere: $g = 10,0\,m/s^2$. $\mu = 1,0\times {10}^{3}\,kg/m^{3}$ e $1,0\,atm =1,0\times {10}{^5}\,N/m^{2}$.
A velocidade de escoamento no andar superior determinaremos pela equação da continuidade.
$\color{Maroon}{S_{1}\times v_{1} = S_{2}\times v_{2}}$$
$S=\frac{\pi D^{2}}{4}$
$\frac{\pi\times{D_{1}}^{2}}{4}\times v_{1} = \frac{\pi\times{D_{2}}^{2}}{4}\times v_{2}$$\Leftrightarrow$$\frac{\pi\times{4,0}^{2}}{\not{4}}\times {0,50} = \frac{\pi\times{2,6}^{2}}{\not{4}}\times v_{2}$
$v_{2}= \frac{\pi\times{4,0}^{2}}\times{0,50}{\pi\times{2,6}^{2}}$$\Leftrightarrow$$v_{2}\simeq 1,183\,m/s$
Calcularemos a pressão de saída usando a Equação de Bernoulli.
$$\color{Maroon}{p_{1} + \mu\times g\times h_{1} + \frac{\mu\times {v_{1}^{2}}}{2} = p_{2} + \mu\times g\times h_{2} +\frac{\mu\times{v_{2}^{2}}}{2}}$$
A incógnita é $p_{2}$. Vamos isolar no primeiro membro.
$p_{2} = p_{1} + \mu\times g\times h_{1} + \frac{\mu\times {v_{1}^{2}}}{2} – \mu\times g\times h_{2} – \frac{\mu\times{v_{2}^{2}}}{2}$
$p_{2}=p_{1} + \left[\frac{\mu\times{(v_{1}^{2} – v_{2}^{2})}}{2}\right] + \mu\times g\times{(h_{1} – h_{2})}$
$p_{2}= {3,0}\times{10}^{5} + \left[\frac{{10}^{3}\times{10,0}\times{({0,50}^{2}-{1,18}^{2})}}{2}\right] + {10}^{3}\times{(0 – 5,0)}$
$p_{2} = {3,0}\times{10}^{5} + \frac{{10}^{3}\times{(0,25 – 1,39)}}{2} – 5,0\times{10}^{4}$
$p_{2} = {3,0}\times{10}^{5} +\frac{{10}^{3}\times{(-1,14)}}{2} – {5,0}\times{10}^{4}$$\Leftrightarrow$$p_{2}={3,0}\times{10}^{5} – {0,057}\times{10}^{4} – {5,0}\times{10}^{4}$
$p_{2} = {30}\times{10}^{4} – 5,057\times{10}^{4}$$\Leftrightarrow$$p_{2}= {24,943}\times{10}^{4}$
$p_{2} = {2,493}\times{10}^{5}\,N/m^{2}$
$$\color{Navy}{p_{2} = 2,493\, atm}$$
Para você fazer
01. A equação da continuidade é uma consequência direta da:
( )a) conservação da energia;
( )b) conservação da massa;
( )c) conservação da quantidade de movimento;
( )d) conservação da carga elétrica;
( )e) conservação da velocidade.
02. Um fluido escoa com $v_{1}=2\,m/s$ em um tubo de área transversal igual a $S_{1}=200\,mm^{2}$. Qual é a velocidade desse fluido ao sair pelo outro lado do tubo, cuja área é de $S_{2}= 100\,mm^{2}$?
( )a) 20 m/s;
( )b) 4 m/s;
( )c) 0,25 m/s;
( )d) 1,4 m/s;
( )e) 0,2 m/s.
03. De acordo com a equação da continuidade, quanto menor for a área disponível para o escoamento de um fluido:
( )a) menor será sua densidade;
( )b) maior será sua densidade;
( )c) menor será sua velocidade;
( )d) maior será sua velocidade;
( )e) menor será sua temperatura.
04. Quando uma torneira é aberta, observa-se que o fluxo de água que sai dela tende a afinar-se. Esse fenômeno pode ser explicado por meio:
( )a) do atrito da água com o ar;
( )b) da conservação da energia mecânica;
( )c) da equação da continuidade;
( )d) das forças intermoleculares presentes na água;
( )e) das ligações de hidrogênio presentes na água.
05. (U.F. Santa Maria-RS) Um líquido incompressível escoa através de uma mangueira cilíndrica de raio $r$ e enche um recipiente de volume $V$ em um intervalo de tempo $\Delta t$. A velocidade média de escoamento do líquido é:
( )a) $\frac{V}{rt}$;
( )b) $\frac{V}{2\pi r\Delta t}$;
( )c) $\frac{V}{\pi r^{2}\Delta t}$;
( )d) $V\pi r^{2}\Delta t$;
( )e) $\frac{V\pi r^{2}}{\Delta t}$.
06. Uma mangueira, com diâmetro interno de $D_{i}=8,0\,cm$, é usada para encher uma piscina circular com diâmetro de $D_{p}= 2,4\,m$. A água flui através da mangueira com uma velocidade média de $v = 0,5\,m/s$. Por quanto tempo essa mangueira deverá ser usada até a água na piscina atingir a profundidade de $h = 0,6\,m$.
07. (UFPA) Considere duas regiões distintas do leito de um rio: uma larga A, com $S_{A}= 200,0\,m^{2}$ de área na secção transversal, onde a velocidade média da água é de$v= 1,0\,m/s;$ outra estreita B, com $S = 40,0\,m^{2}$ de área na secção transversal. Calcule:
a) a vazão volumétrica do rio, em $m^{3}/s$;
b) a velocidade média da água do rio, em $m/s$, na região estreita B.
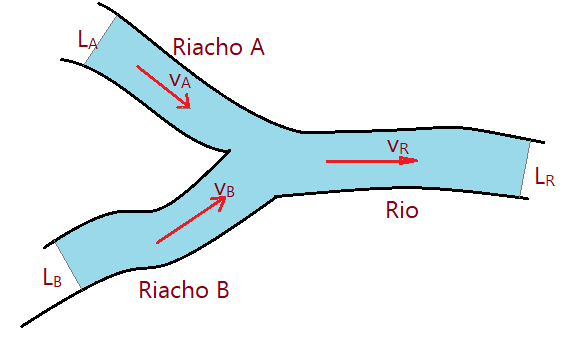
08. A figura abaixo mostra dois riachos, A e B, que se unem para formar um rio. O riacho A tem largura de $L_{A}=2,0\,m$, profundidade de $h_{A} = 0,50\,m$ e a água flui com velocidade de $v_{A} = 4,0\,m/s$. O riacho B tem largura de $L_{B} = 3,0\,m$, profundidade de $h_{B} = 1,0\,m$ e, nesse riacho, a água flui a $v_{B} = 2,0\,m/s$. Determine a profundidade do rio, sabendo que sua largura é de $L_{R} = 5,0\,m$ e que a velocidade de suas águas é de $v_{R} = 2,5\,m/s$.
09. Um duto circular, com raio de $r =15,0\,cm$, é usado para renovar o ar em uma sala, com dimensões de
$10\,m × 5,0\,m × 4,5\,m$, a cada $\Delta t =10\,min$. Qual deverá ser a velocidade média do fluxo de ar através do duto
para que a renovação de ar ocorra conforme desejado?
10. Uma mangueira de jardim tem diâmetro interno de $D_{i}=1,8\,cm$ e está ligada a um irrigador que
consiste apenas de um recipiente com 24 orifícios, cada um com diâmetro de $D_{24} = 0,12\,cm$. Se a velocidade da água na mangueira é de $v =0,90\,m/s$, qual sua velocidade ao sair dos orifícios?
11. Usando os dados do exercício resolvido 3, calcule a velocidade média do fluxo de sangue através das maiores artérias do corpo humano, sabendo que tais artérias têm secção transversal com área de $2,0\,cm^{2}$.
12. (Santa Maria-RS) – Água, cuja densidade é $\mu_{H_{2}O}=10^{3}\,kg/m^{3}$, escoa através de um tubo horizontal, com velocidade de $v_{1} = 2.0\,m/s$, sob pressão de $p =2\times 10^{5}\,N/m^{2}$. Em certo ponto, o tubo apresenta um estreitamento pelo qual a água flui à velocidade de $v_{2} = 8,0\,m/s$. A pressão, nesse ponto, em $N/m^{2}$, é:
( )a) $0,5\times 10^{5}$;
( )b) $1,7\times 10^{5}$;
( )c) $8,0\times 10^{5}$;
( )d) $1,0\times 10^{5}$;
( )e) $4,2\times 10^{5}$.
13. Um galpão é coberto por um telhado com área de $S = 400\,m^{2}$. Um vento forte sopra a $V =72\, km/h$ sobre
esse telhado. O ar dentro do galpão está em repouso e sob pressão de $1,0\,atm$. Considere que a densidade do ar seja $\mu = 1,29\, kg/m^{3}$ e adote $1,0\,atm = 1,0 \times 10^{5}\,N/m^{2}$.
Determine:
a) a diferença de pressão do ar que circunda o telhado(interior e exterior);
b) a força resultante que atua sobre ele.
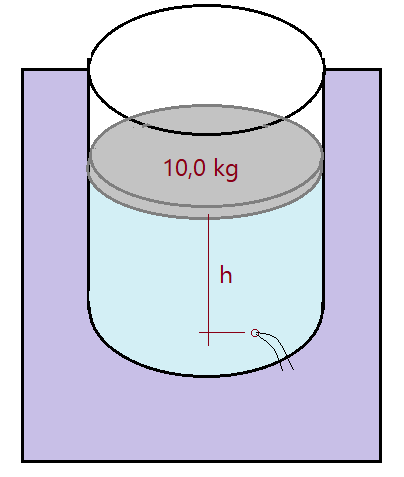
14. Um tanque, com área de secção transversal $S = 0,07\,m^{2}$, contém água ($\mu_{H_{2}O} = 10^{3}\,kg/m^{3}$). Um êmbolo, com massa total $m = 10,0\,kg$, repousa sobre a superfície da água. Um orifício circular, com diâmetro de $D_{1} = 1,5\,cm$ é aberto na parede lateral do reservatório a uma profundidade de $h =60\,cm$ abaixo da superfície da água. Qual é a vazão inicial de água, em litros/s, através do orifício?
15. (UFPA) – A figura abaixo representa um grande
reservatório de água de uma represa, com uma canalização nele acoplada, cujas áreas das secções são $S_{1} = 900\,cm^{2}$
em 1 e $S_{2} = 600\,cm^{2}$ em 2.
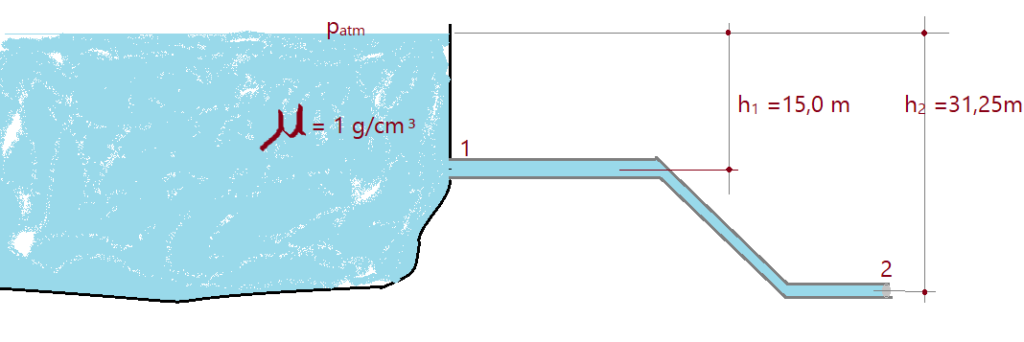
Admita que a água possa ser considerada um fluido ideal e que escoe em regime permanente. Sabendo-se que a aceleração da gravidade vale $g = 10\,m/s^{2}$ e que a pressão atmosférica é igual a $p_{at} = 10^{5}\,N/m^{2}$, pede-se:
a) a velocidade, em $m/s$, com que a água flui no ponto 2;
b) a vazão, em $m^{3}/s$, da água;
c) a pressão, em $N/m^{2}$, no ponto 1.
No próximo post abordaremos algumas aplicações do Teorema de Bernoulli(Equação}, junto com um farto sortimento de exercícios sobre o assunto. Havendo dúvidas, não perca tempo e consulte por um dos canais abaixo. Estou à disposição para ajudar.
Curitiba, 07 de julho de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
