Física – Termologia, Dilatometria.
Dilatação dos líquidos
Será que faz sentido falar em dilatação linear e superficial de líquidos?!
Se você pensar um pouco, verá que não. Colocando um litro de água em uma bacia, ela muda de forma, assumindo a forma da bacia ou de outro recipiente em que for colocada. A superfície livre fica diferente, mas não muda o volume pelo simples fato de trocar de recipiente. Isso também se verifica com os demais líquidos. Todos eles assumem a forma do recipiente em que são postos.
Sendo assim, ficamos apenas com a dilatação volumétrica das substâncias no estado líquido. Isso nos traz um novo detalhe. Se o líquido for aquecido, o recipiente também sofrerá a mesma variação de temperatura e consequentemente se dilatará. Vamos adiantar no momento que o volume interno (capacidade) aumenta como se fosse um bloco maciço. Via de regra o coeficiente de dilatação dos líquidos é maior do que o dos sólidos. Isso nos permite avaliar a dilatação volumétrica dos líquidos, de modo combinado com a dilatação dos recipientes.
$$\color{Blue}{\Delta V = \gamma\times V_{0}\times\Delta\theta}$$
Se temos um recipiente graduado, contendo um volume $V_{0}$ de um determinado líquido, na temperatura inicial $\theta_{0}$ e aquecermos o conjunto a uma temperatura final $\theta$, veremos que o volume indicado na escala graduada terá um novo valor $V_{ap}$. Note que usei um índice formado pelas iniciais de “aparente”, pois uma parte da dilatação do líquido estará dentro da parte do recipiente que o continha antes e também sofreu uma dilatação. Por conseguinte, iremos ter que:
$$\color{Brown}{\Delta V = \Delta V_{ap}+ \Delta V_{r}}$$
Em outras palavras, a dilatação real do líquido é a adição da dilatação aparente com a dilatação do recipiente.
O coeficiente de dilatação do líquido também será resultante da adição do coeficiente aparente com o coeficiente do recipiente.
$$\color{Brown}{\gamma_{L} = \gamma_{ap} + \gamma_{r}}$$
As demais fórmulas serão iguais às usadas para os sólidos.
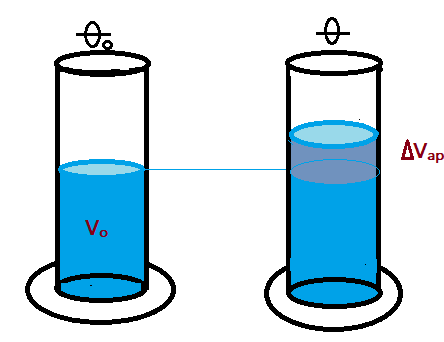
Vejamos a figura ilustrativa
No primeiro recipiente (proveta), temos um volume $V_{0}$ de um líquido, na temperatura $\theta_{0}$. Aquecemos o conjunto à temperatura $\theta$ e observamos uma dilatação aparente do líquido igual a $\Delta V_{ap}$. Enquanto isso a parte não aparente fica contida no segmento do recipiente que também se dilatou. Por isso é necessário fazer uso da adição dessas parcelas.
Tabela de alguns coeficientes de dilatação volumétrica de líquidos
| Substância líquida | $\gamma (^{0}C^{-1})$ |
| Água | $130\cdot{10}^{-6}$ |
| Mercúrio | $180\cdot{10}^{-6}$ |
| Álcool etílico | $1124\cdot{10}^{-6}$ |
| Acetona | $1490\cdot{10}^{-6}$ |
| Glicerina | $490\cdot{10}^{-6}$ |
| Benzeno | $1060\cdot{10}^{-6}$ |
Resolvendo exercícios
01. Determine o coeficiente de dilatação volumétrica de uma porção de $V_{0}=1\,m^{3}$ de líquido que sofre uma dilatação de $\Delta V = 0,05\,m^{3}$, quando aquecido de $\theta_{0}= 25\,^{0}C$ para $\theta = 225\,^{0}C$.
$$\color{Blue}{\Delta V = \gamma\cdot Vtimes_{0}\times \Delta\theta}$$
$\gamma = \frac{\Delta V}{V_{0}\times{(\theta- \theta_{0})}}$$\Leftrightarrow$$\gamma = \frac{0,05}{1\times 200}$
$\gamma = 0,000025 = 25\times{10}^{-6}\,^{0}C^{-1}$
$$\color{Brown}{\gamma = 25\times{10}^{-6}\,^{0}C}^{-1}$$
02. Um frasco de vidro, cujo coeficiente de dilatação volumétrica é de $\gamma = 27\times{10}^{-6}\,^{0}C^{-1}$ apresenta uma capacidade volumétrica de $V_{0}= 1000\, ml$, à temperatura de $\theta_{0} = 20\,^{0}C$, e encontra-se completamente preenchido por um líquido desconhecido. Ao aquecermos o conjunto até $\theta = 120 ^{0}C$, $\Delta V_{ap}= 50\,ml$ de líquido transbordam para fora do recipiente. Determine: a) o coeficiente de dilatação aparente do líquido; b) o coeficiente de dilatação real do líquido; c) e a dilatação sofrida pelo frasco de vidro; d) a dilatação do líquido.
Dados:$\gamma = 27\times{10}^{-6}\,^{0}C^{-1}$; $\theta_{0} = 20^{0}C$; $\theta = 120^{0}C$; $\Delta V_{ap}= 50\,ml$ e $V_{0}= 1000\,ml$
O volume de líquido transborda, corresponde à dilatação aparente do líquido.
a) $$\color{Blue}{\Delta V_{ap}= \gamma_{ap}\times V_{0}\times{(\theta-\theta_{0})}}$$
$\gamma_{ap} = \frac{\Delta V_{ap}}{V_{0}\times{\left(\theta – \theta_{0}\right)}}$
$\gamma_{ap}= \frac{50}{1000\times{(120 – 20)}}$$\Leftrightarrow$$\gamma_{ap}= \frac{50}{100000}=5\times{10}^{-4}\,^{0}C^{-1}$
$$\color{Brown}{\gamma_{ap}=5\cdot{10}^{-4}\,^{0}C^{-1}}$$
b)$$\color{Blue}{\gamma_{L} = \gamma_{ap} + \gamma_{r}}$$
$\gamma_{L}= 5\times{10}^{-4} + 27\times{10}^{-6} = 527\times{10}^{-6}\,^{0}C^{-1}$
$$\color{Brown}{\gamma_{L} = 527\times{10}^{-6}\,^{0}C^{-1}}$$
c)$$\color{Blue}{V_{r} = V_{0}\times{\left(1 + \alpha_{vid}\times {[\theta – \theta_{0}]}\right)}}$$
$V_{r} = {1000}\times{(1 + 27\times{10}^{-6}\times [120 – 20])}$
$V_{r} = {10}^{3}\times{(1 + 0,0027)}$$\Leftrightarrow$$V_{r}= {10}^{3}\times{1,0027} = 1002,7\, ml$
$$\color{Brown}{V_{r} = 1002,7\,ml}$$
d)$$\color{Blue}{\Delta V_{L}= \left(V_{L} – V_{0}\right) + \Delta V_{ap}}$$
$\Delta V_{L} = \left(1002,7 – 1000,0\right) + 50 = 52,7\,ml$
$$\color{Brown}{\Delta V_{L} = 52,7\,ml}$$
03. Um copo graduado de capacidade $V_{0}= 10\,dm^{3}$ é preenchido com álcool etílico, ambos inicialmente à mesma temperatura, e são aquecidos em $\Delta\theta =100\,^{0}C$. Qual foi a dilatação real do álcool? Quanto de álcool transborda do copo? Qual é a dilatação do copo? Qual é o coeficiente de dilatação aparente do álcool? Considere $\gamma_{ae}= {11,24}\times{10}^{-4}\,^{0}C^{-1}$ e $\gamma_{vid}=12\times{10}^{-6}\,^{0}C^{-1}$.
Comecemos por responder à primeira pergunta.
$$\color{Blue}{\Delta V_{ae}= \gamma_{al}\times V_{0}\times \Delta\theta}$$
$\Delta V_{ae}= {11,24}\times{10}^{-4}\times{10}\cdot {100}$$\Leftrightarrow$$\Delta V_{ae}= {11,24}\times {10}^{-1}$
$$\color{Brown}{\Delta V_{ae}=1,124\,dm^{3}}$$
Quanto de álcool transborda? (é a dilatação aparente do álcool)
$$\color{Blue}{\Delta V_{ap} =\gamma_{ap}\times V_{0}\times{10}^{2}}$$
$\Delta V_{ap} = \left({\gamma_{ae} – \gamma_{vid}}\right)\times V_{0}\times{10}^{2}$$\Leftrightarrow$$\Delta V_{ap}= \left({{11,24}\times{10}^{-4}-{12}\times{10}^{-6}}\right)\times 10\cdot {10}^{2}$
$\Delta V_{ap}= \left({1124}\times{10}^{-6} -{12}\times{10}^{-6}\right)\times{10}^{3}$$\Leftrightarrow$$\Delta V_{ap}= {1112}\times{10}^{-6}\times{10}^{3}$
$\Delta V_{ap}={1,112}$$\Leftrightarrow$$\Delta V_{ap} = 1,112\,dm^{3}$
$$\color{Brown}{\Delta V_{ap} = 1,112\,dm^{3}}$$
Vamos à dilatação do copo. Podemos obter esse resultado com o que já calculamos. A dilatação do copo é a diferença entre a dilatação real e a aparente do álcool. Mas também podemos usar a fórmula de calculo da dilatação do copo, que é sólido.
$$\color{Blue}{\Delta V_{vid}= \Delta V_{ae} – \Delta V_{ap}}$$
$\Delta V_{vid}= 1,124 – 1,112 = 0,012$$\Leftrightarrow$$\color{Brown}{\Delta V_{vid}= 0,012\,dm^{3}}$
$$\color{Blue}{\Delta V_{vid} = \gamma_{vid}\times V_{0}\times \Delta\theta}$$
$\Delta V_{vid}= 12\times {10}^{-6}\times{10}\times{10}^{2}$$\Leftrightarrow$$\Delta V_{vid}= 12\times{10}^{-6}\times {10}^{3}= 12\times{10}^{-3}$
$$\color{Brown}{\Delta V_{vid}= 0,012\,dm^{3}}$$
O coeficiente de dilatação aparente do álcool será dado pela diferença entre os coeficientes das duas substâncias.
$$\color{Blue}{\gamma_{ap}= \gamma_{ae} – \gamma_{vid}}$$
$\gamma_{ap} = 11,24\times{10}^{-4} – 12\times{10}^{-6}$$\Leftrightarrow$$ \gamma_{ap}= 1112\times{10}^{-6}\,^{0}C^{-1}$
$$\color{Brown}{\gamma_{ap} = 11,12\times{10}^{-4}\,^{0}C^{-1}}$$
04. Um recipiente de vidro, cujo volume interno é $V_{vid}= 5000,0\, cm^{3}$, está completamente cheio de álcool à temperatura de $\theta_{0}= 20\,^{0}C$. Sabe-se que os coeficientes de dilatação volumétrica do vidro e do álcool são respectivamente $\gamma_{vid}= 27\times{10}^{-6}\,^{0}C^{-1}$ e $\gamma_{ae}= 11\times{10}^{-4}\,^{0}C^{-1}$. Se o conjunto foi aquecido até a temperatura de $\theta =60\,^{0}C$, calcule o volume de álcool que transborda, a dilatação do recipiente e a dilatação real do líquido.
O volume de álcool que transborda é a dilatação aparente do mesmo.
$$\color{Blue}{\Delta V_{ap} = \left({\gamma_{ae} – \gamma_{vid}}\right)\times V_{0}\times\Delta\theta}$$
$\Delta V_{ap}=\left({11\times{10}^{-4} – 27\times{10}^{-6}}\right)\times {5000,0}\times{(60 – 20)}$
$\Delta V_{ap}=\left({1100\times{10}^{-6} – 27\times {10}^{-6}}\right)\times {5000,0}\times {40}$
$\Delta V_{ap}= 1073\times {10}^{-6}\cdot{2}\times{10}^{5}$$\Leftrightarrow$$\Delta V_{ap}= 214,6\, cm^{3}$
$$\color{Brown}{\Delta V_{ap} = 214,6\,cm^{3}}$$
$$\color{Blue}{\Delta V_{vid}= \gamma_{vid}\times V_{0}\times\Delta\theta}$$
$\Delta_{vid}= 27\times{10}^{-6}\times 5\times{10}^{3}\times 40$
$\Delta_{vid} = 27\times{10}^{-6}\times 2\times{10}^{5}$$\Leftrightarrow$$\Delta_{vid}= 54\times {10}^{-1}$
$$\color{Brown}{\Delta V_{vid}=5,4\,cm^{3}}$$
$$\color{Blue}{\Delta V_{ae} = \Delta V_{ap} + \Delta V_{vid}}$$
$\Delta V_{ae}= 214,6 + 5,4 = 220,0\, cm^{3}$$\Leftrightarrow$$\color{Brown}{\Delta V_{ae}= 220,0\,cm^{3}}$
Dilatação anômala da água
Uai! O que significa isso?
A natureza em sua sabedoria ilimitada, fez a água ter um comportamento diferente em termos de dilatação. Para todas as substâncias, os valores dos coeficientes de dilatação são considerados constantes em determinados intervalos de temperatura. Se considerarmos a escala termométrica toda, teríamos um gráfico que não pode ser chamado exatamente uma reta.
No caso da água, esse fato é ainda bastante diferenciado. Ao fundirmos um bloco de gelo, obtemos imediatamente um volume, ligeiramente menor de água a temperatura de $\theta = 0\,^{0}C$. aquecendo essa água, ela irá sofrer uma redução em seu volume, até o instante em que a temperatura chegar ao valor $\theta= 4\,^{0}C$. Depois ela irá se dilatar de modo aproximadamente uniforme na fase líquida, até as proximidades de iniciar o processo de ebulição (ferver), quando irá passar para o estado gasoso, onde o comportamento será outro.
Em consequência disso a água apresenta sua maior densidade ou maior massa específica exatamente na temperatura de $\theta=4\,^{0}C$. Podemos representar num gráfico cartesiano o volume em função da temperatura e também a massa específica em função da temperatura. Veja as figuras abaixo.
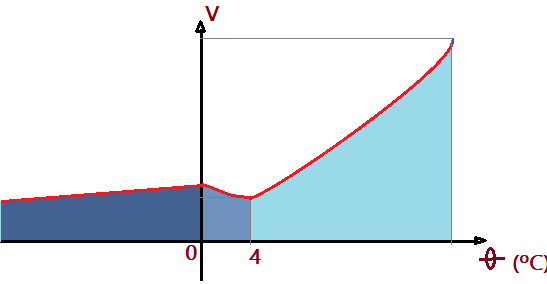
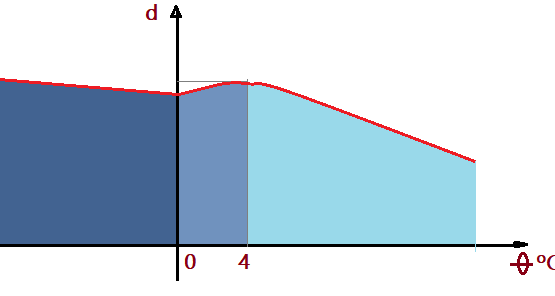
Esse fenômeno tem imenso significado na natureza. Lembrando do Princípio de Arquimedes, podemos deduzir que, no momento em que as partículas de água se solidificam, a sua redução de densidade lhes permite flutuar e assim se forma a crosta de gelo na superfície dos líquidos. Desse modo o fundo dos oceanos é líquido, mesmo que na superfície e por dezenas ou centenas de metros tenhamos uma camada compacta de gelo. Isso permite que a vida nas profundezas se preservae normalmente. A água mais fria fica na superfície, enquanto a mais quente vai para o fundo.
Já nas temperaturas superiores aos $4\,^{0}C$ o processo se inverte. Formam-se as chamadas correntes de convecção, levando as moléculas mais quentes para cima e forçando as mais frias para baixo. Eu sempre vejo essa anomalia como algo “proposital”, destinado a uma finalidade específica a serviço da natureza.
Dilatação de cavidades em sólidos.
Vamos imaginar um cilindro de metal, oco. Se o submetermos a uma elevação de temperatura, o que acontece com a parte oca? Será que ela permanece inalterada, diminui de tamanho ou aumenta de tamanho na proporção do restante do cilindro?
Sabemos que as partículas, moléculas ou átomos, de um corpo sólido ocupam posições fixas no interior da massa do corpo, graças às forças de coesão intensas. Elas vibram, com mais ou menos amplitude, mas a disposição relativa entre elas permanece a mesma. Ao serem submetidas a um aquecimento, elas precisam de mais espaço para vibrar e se viessem para o interior, ou seja, ocupar a parte oca, devido à estrutura cristalina do sólido, elas teriam que ficar mais próximas entre si, o que fica impossível. Desta forma, notamos que o cilindro do nosso exemplo, ou qualquer outro corpo sólido, ao ser aquecido sofre um aumento de sua capacidade volumétrica. Em outras palavras se dilata como se fosse maciço.
Esse comportamento tem uma série de aplicações nos processos industriais, desde os mais rudimentares, até os mais sofisticados, principalmente na hora de ajustar peças metálicas, anelares, cilíndricas e outros formatos. O aquecimento de uma das peças ou o resfriamento de uma ou outra, fazem seus diâmetros se igualarem e assim possibilitar a colocação das mesmas em posição exata e impedir que se desloquem.
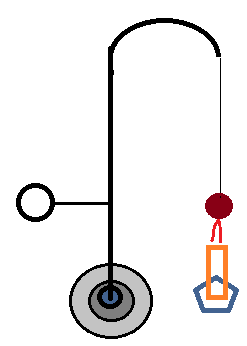
Anel de Gravesande
Um anel metálico e uma esfera que podem ser do mesmo metal ou metais diferentes. Podemos observar que inicialmente a esfera é ligeiramente menor que o interior do anel. Se a vela aquecer a esfera e ocorrer a consequente dilatação, chegará o momento em que a esfera não mais passará pelo interior do anel. A haste que suspende a esfera pode girar, colocando a esfera sobre o anel ou anel pode ser girado para ficar na direção da esfera. Isso mostra a dilatação da esfera em todos os sentidos. O diâmetro é uma medida linear, a superfície e também o volume aumentam com o aquecimento.
Lâminas bimetálicas
Para obter uma lâmina bimetálica devemos soldar duas lâminas de metais diferentes, se isso for possível, ou recorrer ao sistema de “rebites”. Fazemos uma série de furos, não muito distantes entre si e ali colocamos um pino de metal resistente, firmemente ajustado e rebatido, para que fiquem firmemente fixadas uma a outra. Isso irá impedir que deslizem uma ao longo da outra. Se elas estiverem retas na temperatura ambiente, podemos colocar o conjunto em contato com uma fonte de calor para aquecer o sistema. O fato de o metais terem coeficientes de dilatação linear diferentes, fará com que a dilatação seja diferente. Impedidas de deslizar, elas irão se encurvar para um lado. Para qual lado será esse encurvamento.?
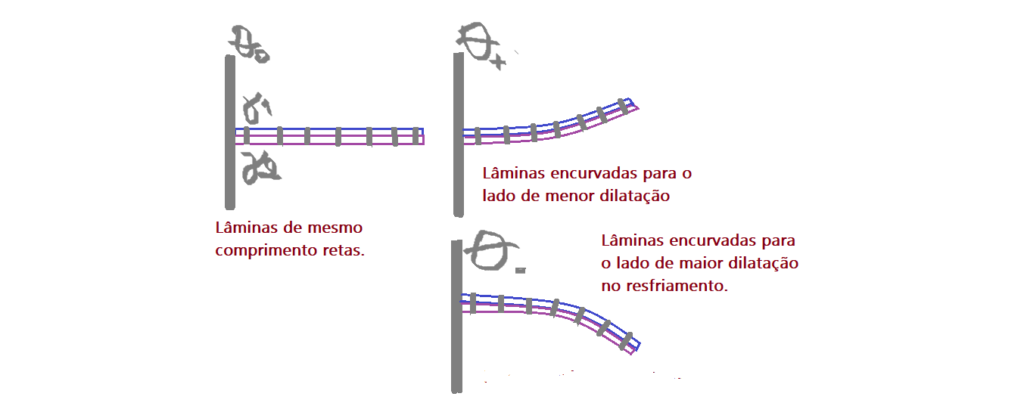
Para responder a essa pergunta é suficiente lembrar que, a lâmina de maior coeficiente de dilatação terá uma dilatação maior e por isso forçará a outra a se encurvar sobre si. Jã quando provocarmos um resfriamento abaixo da temperatura ambiente, a lâmina que irá “encolher” mais será a de maior coeficiente e o encurvamento ocorrerá para o lado dela. Vejamos as ilustrações.
Na figura acima vemos que na temperatura ambiente as duas lâminas estão retas e tem mesmo comprimento. Quando as aquecemos acima dessa temperatura ocorre o encurvamento para o lado da lâmina de $\gamma_{1}$, levando à conclusão de que $\gamma_{1} < \gamma_{2}$. Quando as resfriamos abaixo do ambiente, elas se encurvam mara o lado da lâmina de $\gamma_{2}$, que encolhe mais e puxa a lâmina de $\gamma_{1}$.
Talvez estejas se indagando para que serve isso! Há inúmeras aplicações desse recurso. É muito usado para dispositivos de abertura e fechamento automático de circuitos elétricos, em função da temperatura. Além disso há outras aplicações práticas.
Termógrafo de mola espiral.
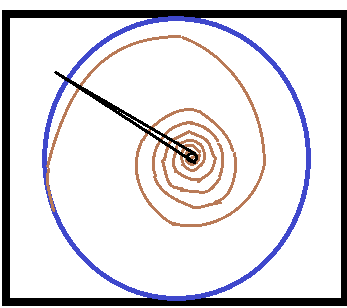
Podemos construir um termógrafo usando uma lâmina metálica flexível, enrolada em forma de espiral, fixada dentro de uma caixa que serve de suporte. Como mostra a figura, a lâmina é fixada na borda e a outra extremidade está ligada, no centro da espiral, a um pequeno eixo que movimenta um ponteiro. Se fizermos a calibração adequada, podemos construir na superfície frontal da caixa uma escala termométrica onde o ponteiro nos indicará a temperatura. Era comum ver esse tipo, tendo um pequeno ímã no verso, para mantê-lo fixo no painel dos automóveis, principalmente antes de surgirem os termômetros digitais, que na maioria das vezes estão embutidos no painel de controle e comandos do veículo.
Exercícios para serem resolvidos
01. Um recipiente de vidro, cujo volume interno é $V_{0} = 200\,cm^{3}$, $\theta_{0} = 20\,^{0}C$, está completamente cheio de um líquido a essa mesma temperatura. Quando o conjunto é aquecido até $\theta = 120\,^{0}C$, há um transbordamento de $\Delta V_{ap}=10\,cm^{3}$ do líquido. Sabendo que o coeficiente de dilatação volumétrica do vidro é $\gamma_{vid}=27\times{10}^{-6}\,^{0}C^{-1}$, calcule: a) o coeficiente de dilatação aparente do líquido; b) o coeficiente de dilatação real do líquido; c) a dilatação volumétrica do recipiente; e) a dilatação real do líquido.
02. (Enem) – A gasolina é vendida por litro, mas em sua utilização como combustível, a massa é o que importa. Um aumento da temperatura do ambiente leva a um aumento no volume da gasolina. Para diminuir os efeitos práticos dessa variação, os tanques dos postos de gasolina são subterrâneos. Se os tanques NÃO fossem subterrâneos:
I. Você levaria vantagem ao abastecer o carro na hora mais quente do dia pois estaria comprando mais massa por litro de combustível
II. Abastecendo com a temperatura mais baixa, você estaria comprando mais massa de combustível para cada litro.
III. Se a gasolina fosse vendida por kg em vez de por litro, o problema comercial decorrente da dilatação da gasolina estaria resolvido
Destas considerações, somente
a) I é correta;
b) II é correta;
c) III é correta;
d) I e II são corretas;
e) II e III são corretas.
03. (Unesp) Nos últimos anos temos sido alertados sobre o aquecimento global. Estima-se que, mantendo-se as atuais taxas de aquecimento do planeta, haverá uma elevação do nível do mar causada, inclusive, pela expansão térmica, causando inundação em algumas regiões costeiras. Supondo, hipoteticamente, os oceanos como sistemas fechados e considerando que o coeficiente de dilatação volumétrica da água é aproximadamente $\gamma_{ag}=2\times{10}^{-4}\,^{0}C^{-1}$ e que a profundidade média dos oceanos é de $p_{m}= 4\,km$, um aquecimento global de $1\,^{0}C$ elevaria o nível do mar, devido à expansão térmica, em, aproximadamente:
a) 0,3 m;
b) 0,5 m;
c) 0,8 m;
d) 1,1 m;
e) 1,7 m.
04. (Ufu) Um frasco de capacidade para $V_{0}= 10\,litros$ está completamente cheio de glicerina e encontra-se à temperatura de $\theta_{0}= 10\,^{0}C$. Aquecendo-se o frasco com a glicerina até atingir $\theta = 90\,^{0}C$, observa-se que $\Delta V_{ap}=352\,ml\, (0,352\, l)$ de glicerina transborda do frasco. Sabendo-se que o coeficiente de dilatação volumétrica da glicerina é $\gamma_{gl}= 5,0\cdot{10}^{-4}/^{0}C$, o coeficiente de dilatação linear do frasco é, em $^{0}C^{-1}$.
a)$6,0\cdot{10}^{-5}$;
b) $2,0\cdot{10}^{-5}$;
c)$4,4\cdot{10}^{-4}$;
d)$1,5\cdot{10}^{-4}$;
e)$3,2\cdot{10}^{-4}$.
05. Uma proveta é recheada completamente com $V_{0}= 400\,cm^{3}$ de um líquido a temperatura $\theta_{0}= 200\,^{0}C$. O conjunto é aquecido à $\theta = 220\,^{0}C$, provocando um transbordamento de $\Delta V_{L}= 40\, cm^{3}$. É dado que $\gamma_{vid}= 24\cdot{10}^{-6}\,^{0}C^{-1}$. Calcule:a) o coeficiente de dilatação aparente do líquido; b) o coeficiente de dilatação real do líquido.
06. Uma panela de ferro de $V_{0}=4\,litros$, está totalmente preenchida com água. Após um aquecimento que eleva a temperatura em $\Delta\theta=50^{0}C$, uma parte da água transborda. Sabe-se que os coeficientes de dilatação volumétrica da água e do ferro são, respectivamente, $\gamma_{ag}=1,3\cdot{10}^{-4}\,^{0}C^{-1}$ e $\gamma_{Fe}=3,9\cdot{10}^{-5}\,^{0}C^{-1}$. Calcule o volume da água transbordada.
07. Um frasco de vidro de $V_{V}=250\,ml$ de álcool a uma temperatura de $\theta_{0}=40\,^{0}C$. A que temperatura o álcool começará a transbordar do frasco? Considere o coeficiente de dilatação linear do vidro igual a $\alpha_{V}=8\times{10}^{-6}\,^{0}C^{-1}$ e o coeficiente volumétrico do álcool é $\gamma_{al}=11,2\times{10}^{-4}\,^{0}C^{-1}$.
08. A respeito da dilatação dos líquidos e da dilatação irregular da água, marque o que for falso.
a) No aquecimento da água entre $0\,^{0}C$ e $4\,^{0}C$, ocorre aumento de volume;
b) A $4\,^{0}C$, a água assume a sua maior densidade dentro do intervalo de $0\,^{0}C$ a $4\,^{0}C$;
c) A dilatação irregular da água ocorre somente em recipientes com coeficiente de dilatação que corresponda ao dobro do valor do coeficiente de dilatação da água;
d) Pode-se considerar que, entre $0\,^{0}C$ e $4\,^{0}C$, o coeficiente de dilatação da água é negativo.
09. Um recipiente de vidro comum, de coeficiente de dilatação linear igual a $\alpha_{v}=9,0\times{10}^{-6}\,^{0}C^{-1}$, está completamente cheio de álcool etílico, de coeficiente de dilatação volumétrica igual a $\gamma_{ae}={0,75}\times{10}^{-3}\,^{0}C^{-1}$. Após o conjunto sofrer uma variação de temperatura $\Delta\theta$, ocorre vazamento de líquido. Determine o valor aproximado do coeficiente de dilatação volumétrica aparente para o álcool etílico.
a)$\gamma_{ap} = 1,23\times{10}^{-4}\,^{0}C^{-1}$;
b)$\gamma_{ap}=6,0\times{10}^{-4}\,^{0}C^{-1}$;
c)$\gamma_{ap}=6,23\times{10}^{-4}\,^{0}C^{-1}$;
d)$\gamma_{ap}=7,23\times{10}^{-4}\,^{0}C^{-1}$;
e)$\gamma_{ap}=2,23\times{10}^{-4}\,^{0}C^{-1}$.
10. (AFA) – Um recipiente de vidro de $V_{0}=200\,ml$ está completamente cheio de mercúrio, e ambos se encontram a $\theta_{0}=30\,^{0}C$. Se a temperatura do sistema líquido-recipiente sobe para $\theta= 90\,^{0}C$, qual é o volume de mercúrio, em $ml$, que transborda do recipiente?
Dados: $\gamma_{Hg}= 1,8\times{10}^{-4}\,^{0}C^{-1}$; $\gamma_{vidro}=3,0\times{10}^{-5}\,^{0}C^{-1}C$
a) 1,8
b) 2,6
c) 5,0
d) 9,0
11. (AFA) – Um recipiente tem capacidade de $V_{0} = 3000\,cm^{3}$ a temperatura de $\theta_{0}=20\,^{0}C$ e está completamente cheio de um determinado líquido. Ao aquecer o conjunto até $\theta = 120\,^{0}C$, transbordam $\Delta V_{ap}= 27\,cm^{3}$. O coeficiente de dilatação aparente desse líquido, em relação ao material de que é feito o recipiente, é, em $^{0}C^{-1}$, igual a:
a) $3,0\times{10}^{-5}$;
b) $9,0\times{10}^{-5}$;
c) $2,7\times{10}^{-4}$;
d) $8,1\times{10}^{-4}$.
12. (Unimep-SP) Quando um frasco completamente cheio de líquido é aquecido, verifica-se um certo volume de líquido transbordado. Esse volume mede:
a) a dilatação absoluta do líquido menos a do frasco;
b) a dilatação do frasco;
c) a dilatação absoluta do líquido;
d) a dilatação aparente do frasco;
e) a dilatação do frasco mais a do líquido.
13. (Unifor-CE) Um recipiente de vidro de capacidade $V_{0}=500\,cm^{3}$, contém $V_{L}=200\,cm^{3}$ de mercúrio, a $\theta_{0}=0\,^{0}C$. Verifica-se que, em qualquer temperatura, o volume da parte vazia é sempre o mesmo. Nessas condições, sendo $\gamma_{Hg}$ o coeficiente de dilatação volumétrica do mercúrio, o coeficiente de dilatação linear do vidro vale:
a) $\alpha_{vid}=\frac{5}{6}\gamma_{Hg}$;
b) $\alpha_{vid}=\frac{5}{3}\gamma_{Hg}$;
c) $\alpha_{vid}=\frac{1}{5}\gamma_{Hg}$;
d) $\alpha_{vid}=\frac{2}{15}\gamma_{Hg}$;
e) $\alpha_{vid}={15}\cdot\gamma_{Hg}$.
Se persistirem dúvidas sobre o assunto abordado ou qualquer outro relacionado ao tema, use os canais abaixo para se comunicar e trataremos de sanar suas dificuldades.
Curitiba, 22 de maio de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
