Física – Movimento Harmônico Simples – MHS
Tal como em grande parte dos fenômenos físicos, as equações são determinadas a partir de modelos idealizados de corpos e suas características. Vejamos um disco, que gira em torno de um eixo horizontal. Na borda do disco fixamos uma esfera por meio de um pino. Colocamos acima do disco um sistema refletor de luz, projetando uma sombra da esfera sobre uma superfície horizontal. Enquanto o disco gira em MCU, a sombra da esfera irá executar um movimento de vai-vem sobre a superfície horizontal. O MCU é um movimento periódico, acontecendo o mesmo com a sombra da esfera. O movimento da projeção será um perfeito MHS. Dele podemos deduzir as fórmulas que iremos utilizar nos cálculos com vários tipos de osciladores.
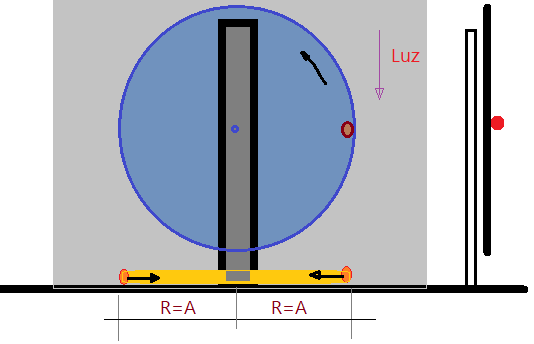
Vamos estudar o movimento dessa projeção, partindo das equações do MCU-Movimento Circular Uniforme.
Vejamos a figura esquemática que segue e apliquemos um pouco de raciocínio, na comparação do movimento circular e do movimento oscilatório da projeção. Ambos têm o mesmo período e esse é nosso ponto de partida.
Pulsação ou velocidade angular do MCU equivalente
$$\color{Maroon}{\omega = \frac{2\pi}{T} = 2\pi f}$$
Cada oscilação do MHS equivale a uma volta do MCU, daí a velocidade angular ser chamada pulsação ou frequência angular.
Começamos por exprimir a posição $X$ em função das demais grandezas. A projeção da esfera fixa ao disco em MCU, se encontra em dado instante nesta posição.
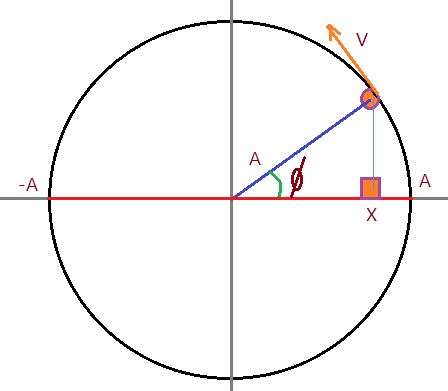
A equação horária angular do MCU nos dá:
$$\color{Blue}{\phi = \phi_{0} + \omega\cdot t}$$.
Esta expressão representa, no MHS da projeção, a fase em que se encontra.
A posição da projeção para essa posição será dada por:
$$\color{Brown}{X = A\times cos({\omega t + \phi_{0}})}$$
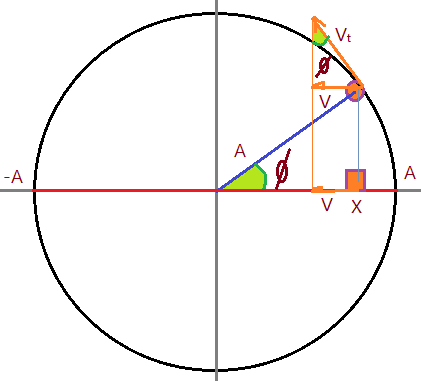
A velocidade da projeção, será a componente da velocidade tangencial do MCU, projetada sobre o eixo $OX$ e será negativa, uma vez que tem o sentido oposto ao semi-eixo $OX$.
Do MCU temos que
$$\color{Blue}{v = \omega\times t}$$.
$\color{Brown}{v = -\omega\times A\times sen({\omega t + \phi_{0}})}$
A aceleração em cada ponto do movimento harmônico simples, será a componente da aceleração do MCU, que é a aceleração centrípeta, dirigida radialmente para o centro do círculo.
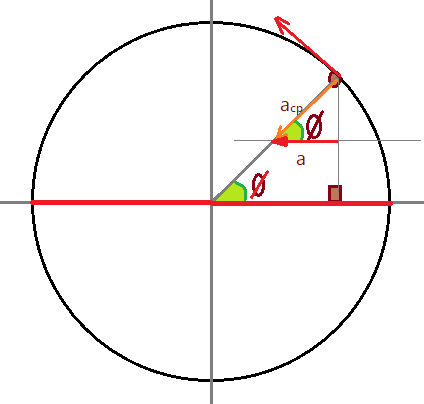
$$\color{Blue}{a_{cp} = \frac{v^{2}}{R}}$$
$$\color{Blue}{a_{cp} = \omega^{2}\cdot R}$$
Temos que $R = A$ e então:
$$\color{Brown}{a = -\omega^{2}\times A\cos({\omega\times t + \phi_{0}})}$$
Relações paramétricas do MHS:
$X = Acos({\omega t + \phi_{0}})$$\Leftrightarrow$$\frac{X}{A} = cos({\omega t + \phi_{0}})$ (1)
$V = -\omega \times A\times({\omega t +\phi_{0}})$$\Leftrightarrow$$\frac{V}{-\omega\times A} = sen({\omega t + \phi_{0}})$ (2)
Elevando (1) e (2) ao quadrado teremos:
$$\left(\frac{X}{A}\right)^{2} = cos^{2}({\omega t + \phi_{0}})$$ (3)
$$\left(\frac{V}{-\omega\times A}\right)^{2} = sen^{2}({\omega t + \phi_{0}})$$ (4)
Somando membro a membro estas duas equações (3) e (4), ficamos com:
$\left(\frac{X}{A}\right)^{2} + \left(\frac{V}{-\omega\times A}\right)^{2} = \underbrace{cos^{2}({\omega t + \phi_{0}}) + sen^{2}({\omega t + \phi_{0}})}$
$\underbrace{cos^{2}({\omega t + \phi_{0}}) + sen^{2}({\omega t + \phi_{0}})} = 1$
$$\color{Brown}{\left(\frac{X}{A}\right)^{2} + \left(\frac{V}{-\omega\cdot A}\right)^{2} = 1}$$
Representação gráfica das grandezas.
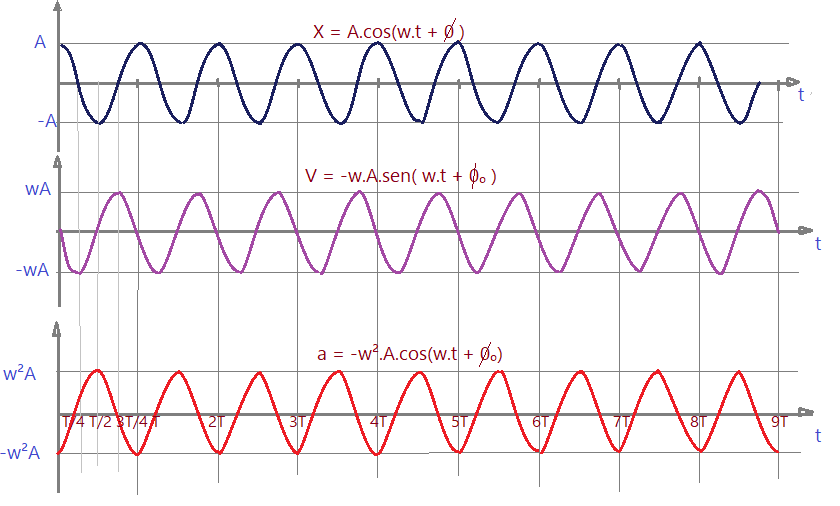
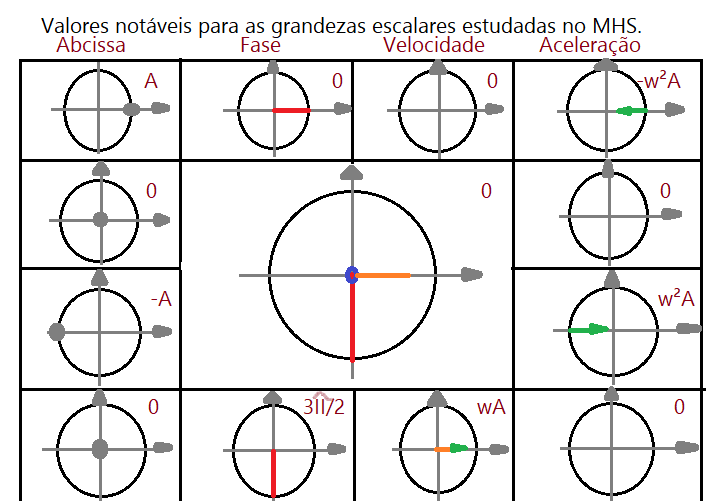
Comparando $X$ e $a$, vamos ter:
$$X = A\times cos({\omega t + \phi{0}})$$ (5)
$$a = -\omega^{2}\times A\times cos({\omega t + \phi_{0}})$$ (6)
Substituindo (5) em (6):
$$\color{Brown}{a = -\omega^{2}\times x}$$
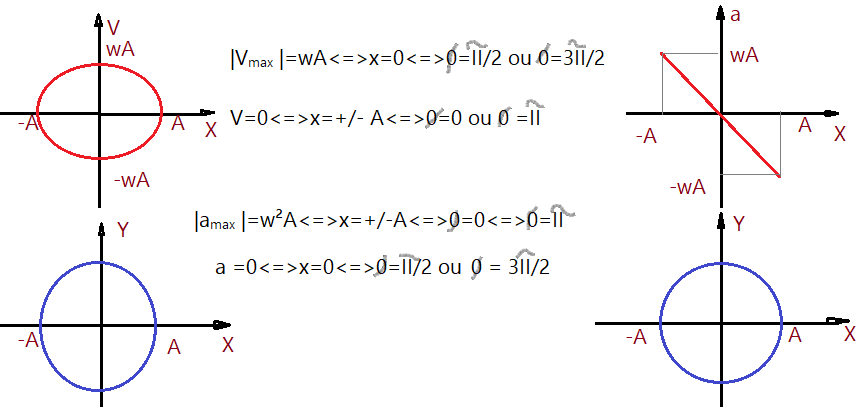
Lembrando da força elástica
Ao estudarmos a elasticidade, vimos que:
$$\color{Blue}{F = – k\times x}$$
Um corpo indeformável, perfeitamente liso, preso à extremidade de uma mola ideal (sem peso), está apoiado sobre uma superfície horizontal, perfeitamente lisa. A outra extremidade da mola está fixada a um ponto da parede. Afastando o corpo da posição de equilíbrio, provocamos uma deformação na mola. A força elástica da mola tende a restaurar a posição de equilíbrio, acelerando o corpo a partir do repouso. Ao alcançar a posição de equilíbrio a força se anula, mas o corpo adquiriu velocidade que lhe confere uma quantidade de movimento. A partir desse ponto a mola começa a sofrer uma compressão, enquanto o corpo gradualmente desacelera, até parar. Como estamos tratando de uma condição ideal, a deformação de compressão da mola será igual em módulo à elongação inicial.
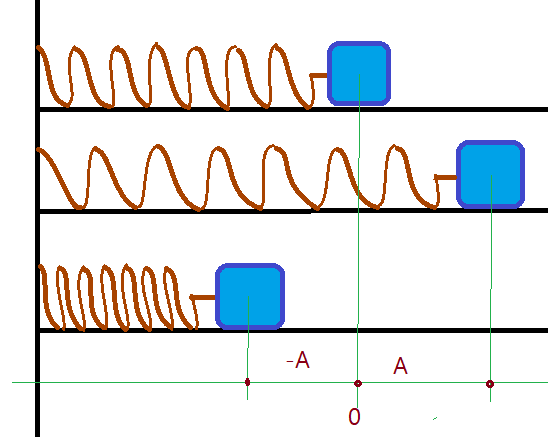
O processo se repete e podemos dizer que o sistema oscila em um MHS. Na prática isso não é exato, mas se aproxima bastante, desde que seja respeitado o limite de elasticidade da mola.
Pelas expressões vistas para o MHS, podemos estabelecer:
$$ F_{restauradora} = F_{elástica}$$
$m\cdot a = k\times x$$\Leftrightarrow$$m\times \omega^{2}\times{\not{x}} = k\cdot {\not{x}}$
$m\cdot \omega^{2} = k$$\Leftrightarrow$$\omega^{2} = \frac{k}{m}$
$\sqrt{\omega^{2}} = \sqrt{\frac{k}{m}}$$\Leftrightarrow$$\omega = \sqrt{\frac{k}{m}}$
Sabemos que $\omega = 2\pi\times f$$\Leftrightarrow$$ \omega = \frac{2\pi}{T}$
Substituindo na expressão anterior, teremos:
$$\color{Brown}{f = \frac{1}{2\times\pi}\sqrt{\frac{k}{m}}}$$
$$\color{Brown}{T = 2\times\pi\sqrt{\frac{m}{k}}}$$
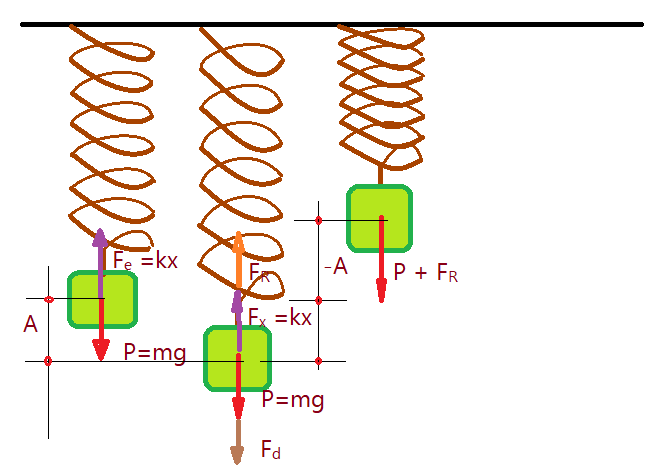
O mesmo acontece com um corpo suspenso pela extremidade de uma mola ideal, fixada na outra a um suporte no teto. Aqui a deformação na posição de equilíbrio é causada pelo peso do corpo. Para fazer o sistema oscilar, executando o que se aproxima de um MHS, é necessário puxar o corpo até uma posição abaixo da de equilíbrio e soltar. O comportamento será o mesmo da outra situação em que o corpo se desloca na horizontal sobre o plano perfeitamente liso. Na posição mais baixa, teremos a força elástica igual à força restauradora adicionada ao peso do corpo. A partir da posição de equilíbrio o peso fica maior que a força elástica, passando a retardar o movimento até parar. Imediatamente depois recomeça o movimento descendente, passa pelo equilíbrio mas segue devido à velocidade adquirida, até atingir novamente o ponto de elongação máxima. Podemos aplicar as mesmas equações do caso anterior.
Pêndulo simples
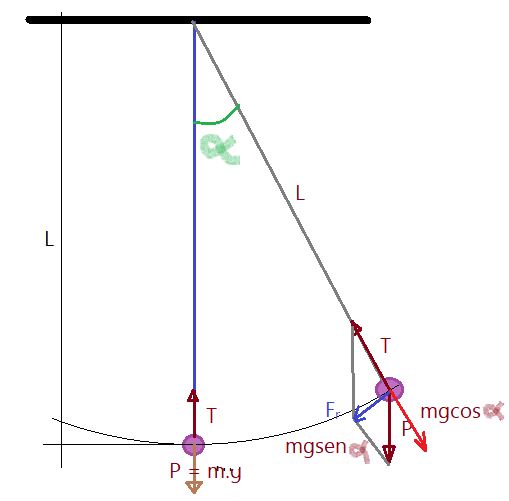
Denominamos pêndulo simples a um fio fino, resistente, mas inextensível, fixado em um gancho no alto, tendo a outra extremidade presa à um corpo uniforme e de massa significativa. A forma da massa deve ser de forma aerodinâmica adequada, sem ter pontos que provoquem um arrasto no ar que o circunda.
Se o pêndulo oscilar com abertura (ângulo) $\alpha \lt 10^{0}$, podemos fazer a aproximação, igualando o ângulo com o valor de seu seno. Sendo então a força restauradora igual a:
$sen\alpha \simeq \alpha = \frac{x}{L}$
$F_{rest} = mg\alpha$$\Leftrightarrow$$ F_{rest}= mg\times\frac{x}{L}$
$F_{rest} =k\times x = mg\times\frac{x}{L}$$\Leftrightarrow$$ k =\frac{m\times g}{L}$
$T= 2\pi\sqrt{\frac{m}{\frac{m\times g}{L}}}$$\Leftrightarrow$$T=2\pi\sqrt{\frac{\not{m}\times L}{\not{m}\times g}}$
$$\color{Brown}{T = 2\pi\sqrt{\frac{L}{g}}}$$
Substituindo em $f = \frac{1}{T}$, fica:
$$\color{Brown}{f = \frac{1}{2\pi}\sqrt{\frac{g}{L}}}$$
Obs.: Nos anos 1980/84 eu lecionava na então UCP, no primeiro ano de engenharia civil e fazia a experiência no laboratório, usando um pêndulo com comprimentos acima de $L\ge1,5 m$. Ele oscila lentamente. Havia vários cronômetros e alunos com relógios que eram também cronômetros. Medíamos o tempo de vinte oscilações para cada comprimento, variando de $10 cm$ cada vez. Isso nos permitiu determinar o valor da aceleração da gravidade com uma aproximação muito boa. Em uma ocasião chegamos muito próximo do valor $g = 9,80 m/s^{2}$. Usando comprimentos menores, fica menos preciso, pois a amplitude precisa ser muito pequena, dificultando a medição mais exata do tempo, para determinar o período.
Vamos exercitar:
01. Uma mola de constante elástica igual a$k= 10,0\,N/m$ é presa a uma massa de $100\,g$ ou $ (0,1 kg)$. Quando comprimida, essa mola passa a oscilar, descrevendo um movimento harmônico simples. Determine a frequência de oscilação do conjunto.
Dados: $$ k = 10,0\,N/m$$
$$ m = 100,0\, g = 0,1\,kg$$
$$\color{Blue}{f= \frac{1}{2\pi}\sqrt{\frac{k}{m}}}$$
$f = \frac{1}{2\pi}\sqrt{\frac{10,0}{0,1}}$$\Leftrightarrow$$f =\frac{1}{2\pi}\sqrt{100}$
$f = \frac{1}{2\pi}\times 10,0 =\frac{5}{\pi}\,Hz$
$$\color{Brown}{f = 1,59\, Hz}$$
02. Prende-se uma mola de constante elástica igual a$k = 1,6\,N/m$ a uma massa de$m = 0,025\,kg$. Após um estímulo, o conjunto passa a oscilar em movimento harmônico simples. Determine a frequência angular do movimento ou velocidade angular do MCU equivalente.
$$\color{Blue}{k = 1,6\,N/m}$$
$$\color{Blue}{m = 0,025\,kg}$$
$$\color{Blue}{w = \sqrt{\frac{k}{m}}}$$
$w = \sqrt{\frac{1,6}{0,025}} = \sqrt{64,0} = 8\,rad/s$
$$\color{Brown}{w = 8\,rad/s}$$
03. Em relação ao movimento descrito por um sistema massa-mola ideal, livre de quaisquer forças dissipativas, assinale a alternativa correta:
( )a) A energia cinética desse movimento permanece constante;
( )b) A frequência do movimento é proporcional à massa do corpo que é preso à mola.
( )c) O período desse movimento depende diretamente da aceleração da gravidade local.
( )d) Nesse tipo de sistema, a energia mecânica não se altera, uma vez que não há presença de forças dissipativas.
( )e) A energia potencial elástica nesse tipo de movimento só diminui.
04. Um oscilador massa-mola, cuja massa é$m = 1,0\,kg$, oscila a partir de sua posição de equilíbrio. Sabendo que a constante elástica da mola é $k=60,0\,N/m$, calcule a velocidade angular e a frequência desse oscilador.
$$\color{Blue}{m = 1,0\,kg}$$
$$\color{Blue}{k = 60,0\,N/m}$$
$$\color{Blue}{w = \sqrt{\frac{k}{m}}}$$
$$\color{Blue}{f = \frac{1}{2\pi}\sqrt{\frac{k}{m}}}$$
$w = \sqrt{\frac{k}{m}} = \sqrt{\frac{60,0}{1,0}}$$\Leftrightarrow$$w ={2}\sqrt{15}$
$$\color{Brown}{w ={2}\sqrt{15}\,rad/s}$$
$f = \frac{1}{2\pi}\sqrt{\frac{60,0}{1,0}}$$\Leftrightarrow$$f=\frac{1}{2\pi}\cdot 2\sqrt{15}$
$$\color{Brown}{f = \frac{1}{\pi}\sqrt{15}\, Hz= 1,23\,Hz}$$
05. Um corpo de massa $m = 3,0\,kg$ está preso a uma mola de constante elástica $k = 200,0\,N/m$. Quando ele é deslocado da sua posição de equilíbrio, passa a deslocar-se, executando o movimento harmônico simples e atingindo uma elongação máxima na posição $\Delta X= 0,5\,m$. Determine a frequência e a amplitude desse movimento.
Dados: $$\color{Blue}{m = 3,0\,kg}$$, $$\color{Blue}{k = 200,0\,N/m}$$
$$\color{Blue}{f = \frac{1}{2\pi}\sqrt{\frac{k}{m}}}$$
$ f= \frac{1}{2\pi}\sqrt{\frac{200,0}{3,0}}$$\Leftrightarrow$$f=\frac{1}{2\pi}\sqrt{\frac{100\cdot 2}{3,0}}$
$f = \frac{1}{2\pi}\cdot 10\sqrt{\frac{2}{3}}$$\Leftrightarrow$$f= \frac{5}{\pi}\sqrt{\frac{2}{3}}$
$$\color{Brown}{f \simeq 1,299\,Hz}$$
A amplitude é igual a elongação máxima, portanto $\color{Blue}{A = 0,5\, m}$
06. Um pêndulo simples tem comprimento $\color{Blue}{L = 1,90\,m}$ e em sua extremidade inferior temos uma esfera de chumbo, com $\color{Blue}{m = 100,0\,g}$. Sendo a aceleração da gravidade local $\color{Blue}{g=9,81\, m/s^{2}}$, determine o período de oscilação e a frequência com que ele oscila.
$$\color{Blue}{T = 2\pi\sqrt{\frac{L}{g}}}$$
$T = 2\pi\sqrt{\frac{1,90}{9,81}}$$\Leftrightarrow$$T=2\pi\cdot {0,44}= 2,765 s$
$$\color{Brown}{T = 2,765\,s}$$
$$\color{Blue}{f = \frac{1}{2\pi}\sqrt{\frac{g}{L}}}$$
$ f = \frac{1}{2\pi}\sqrt{\frac{9,81}{1,90}}$$\Leftrightarrow$$f = \frac{1}{2\pi}\cdot{2,272}\simeq 0,362\,Hz$
$$\color{Brown}{f \simeq 0,362\,Hz}$$
07. Uma massa de $\color{Blue}{m = 200,0\,g}$, oscila em forma de pêndulo simples suspenso de um cabo fino, inextensível e massa desprezível, com período de $\color{Blue}{T = 3,0\,s}$. Sendo $\color{Blue}{g = 9,80\, m/s^{2}}$, determine o comprimento do cabo.
$$\color{Blue}{T= 2\pi\sqrt{\frac{L}{g}}}$$
$ 3,0 = 2\pi\sqrt{\frac{L}{9,80}}$$\Leftrightarrow$$ {3,0}^{2} ={(2\pi)}^{2}\cdot\sqrt{\frac{L}{9,80}}^{2}$
$9,0 = 4,0\pi^{2}\cdot \frac{L}{9,8}$$\Leftrightarrow$${9,0}\cdot {9,80} = 4,0\pi^{2}\cdot L$
$\frac{88,2}{4\pi^{2}} = L$$\Leftrightarrow$$ L = 2,234\,m$
$$\color{Brown}{L = 2,234\,m}$$
Exercícios para resolver
01. Um pêndulo simples, de comprimento $\color{Blue}{L=1,75\,m}$, oscila com frequência $\color{Blue}{f = 0,25\,Hz}$. Determine a aceleração da gravidade no local em que ocorre essa oscilação e a frequência angular do movimento.
02. Uma mola tem constante elástica $\color{Blue}{k = 80\,N/m}$. Em sua extremidade livre está fixado um corpo indeformável, de $\color{Blue}{m= 50,0\,kg}$ e é posta a oscilar a partir de uma elongação de $\color{Blue}{x = 0,40\,m}$. Determine: a) o período de oscilação do sistema; b) a frequência de oscilação; c) a velocidade angular do MCU equivalente; d) a velocidade máxima do corpo; e) a energia potencial da mola na elongação máxima.
03. Um sistema massa mola oscila com frequência de $\color{Blue}{f= 0,5\, Hz}$. Sendo a massa do corpo de $\color{Blue}{m = 2,0\,kg}$, determine a constante elástica da mola, o período de oscilação, a energia potencial da mola na elongação máxima e a energia mecânica do sistema.
04. Um pêndulo simples de $\color{Blue}{L= 1,69\,m}$, oscila dentro do limite de $\color{Blue}{\alpha\le 10^{0}}$. Sendo a gravidade local $\color{Blue}{g=10,0\,m/s^{2}}$. Qual é o período de oscilação? Qual é a frequência com que o sistema oscila?
05. Uma esfera de massa igual a $\color{Blue}{m = 0,2\,kg}$ está presa a uma mola, cuja constante elástica $\color{Blue}{k = 0,8\pi^{2}\,N/m}$. Afasta-se a mola $\color{Blue}{A = 3\,cm}$ de onde estava em repouso e ao soltá-la o conjunto massa-mola começa a oscilar, executando um M.H.S. Desprezando as forças dissipativas, determine o período e a amplitude do movimento.
06. Em uma mola, cuja constante elástica é $\color{Blue}{k = 65\,N/m}$, está acoplado um bloco de massa $\color{Blue}{m = 0,68\,kg}$. Movendo o bloco da posição de equilíbrio, $\color{Blue}{x = 0}$, até uma distância de $\color{Blue}{A = 0,11\,m}$ e soltando-o do repouso em $\color{Blue}{t = 0}$, determine a frequência angular e a aceleração máxima do bloco.
07. (Mack-SP) – Uma partícula descreve um movimento harmônico simples segundo a equação $x = 0,3\times cos(\frac{\pi}{3} + 2 t)$, no SI. O módulo da máxima velocidade atingida por esta partícula é:
( )a) $3\pi\,m/s$;
( )b) $0,2\pi\,m/s$;
( )c) $0,6\,m/s$;
( )d) $0,1\pi\,m/s$;
( )e) $0,3\,m/s$.
08. Se a posição de uma partícula é determinada pela função horária $x = 2 cos{(4\pi t + \frac{\pi}{2})}$, qual a velocidade escalar da partícula quando $t = 1\,s$?
( )a)$v = -6\pi\,m/s$;
( )b)$v = -8\pi\,m/s$;
( )c)$v = -4\pi\,m/s$;
( )d)$v= -2\pi\,m/s$;
( )e)N.d.a.
09. Calcule a frequência angular de uma partícula que desenvolve um movimento harmônico simples sabendo que o período desse movimento equivale a $T= 0,5\,s$.
( )a)$\frac{\pi}{2}\,rad/s$;
( )b)$\pi\,rad/s$;
( )c)$4\pi\,rad/s$;
( )d)$3\frac{\pi}{2}\,rad/s$;
( )e)$\frac{3\pi}{5}\,rad/s$.
10. Uma partícula descreve um movimento harmônico simples de amplitude igual a $A =4\,cm$. Sabendo que a fase inicial do movimento é igual a $\phi = 0$ e que sua frequência angular é igual a$\omega = \pi\,rad/s$, determine a posição dessa partícula no instante $t = 0,5\,s$.
( )a) 2\,cm;
( )b) 5\,cm;
( )c) 0\,cm;
( )d) 4\,cm;
( )e) 3,0\,cm.
11. Determine a velocidade máxima de um móvel que descreve um movimento harmônico simples de amplitude igual a $A = 5\,m$ sabendo que sua velocidade angular é igual a $\omega = 2\pi\,rad/s$.
( )a) $2\pi\,m/s$;
( )b) $10\pi\,m/s$;
( )c) $\pi\,m/s$;
( )d) $\frac{\pi}{4}\,m/s$;
( )e) $3\pi\,m/s$.
12. (Unitau-SP) – Um corpo de massa $m$, ligado a uma mola de constante elástica $k$, está animado de um movimento harmônico simples. Nos pontos em que ocorre a inversão no sentido do movimento:
( )a) são nulas a velocidade e a aceleração;
( )b) são nulas a velocidade e a energia potencial;
( )c) o módulo da aceleração e a energia potencial são máximas;
( )d) a energia cinética é máxima e a energia potencial é mínima;
e) a velocidade, em módulo, e a energia potencial são máximas.
13. (Osec-SP) – Um móvel executa um movimento harmônico simples de equação $x = 8\cdot cos\left(\frac{\pi}{8}\cdot t\right)$ onde $t$ é dado em segundos e $x$ em metros. Após $t = 2,0\,s$, a elongação do movimento é:
( )a) zero;
( )b) 2,0\,m;
( )c) 3,5\,m;
( )d) 5,7\,m;
( )e) 8,0\,m.
14. Um oscilador massa-mola, cuja massa é $m =1\,kg$, oscila a partir de sua posição de equilíbrio. Sabendo que a constante elástica da mola é $k = 60\,N/m$, calcule a velocidade angular e a frequência desse oscilador.
15. Um corpo de massa $m = 3\,kg$ está preso a uma mola de constante elástica $k = 200\,N/m$. Quando ele é deslocado da sua posição de equilíbrio, passa a deslocar-se, executando o movimento harmônico simples e atingindo uma elongação máxima na posição $x_{max}=0,5\,m$. Determine a frequência e a amplitude desse movimento.
16. Um móvel executa um movimento harmônico simples segundo a seguinte equação: $x = 4\times cos{(\pi\times t + \pi)}$, no S.I.
Determine a amplitude do movimento, \ pulsação, a fase inicial, o período e a frequência do movimento.
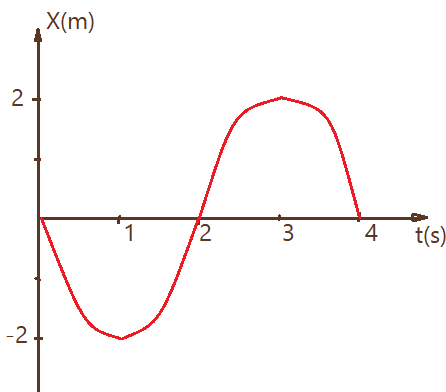
17. (UFG) – O gráfico mostra a posição, em função do tempo, de uma partícula em movimento harmônico simples no intervalo de tempo entre 0 e 4 segundos. A equação da posição em função do tempo para esse movimento é dada por $x = A\times cos{(\omega t + \phi_{o})}$. A partir do gráfico, encontre os valores das constantes $A$, $\omega$ e $\phi_{o}$.
18. Determine os períodos dos ponteiros de um relógio e calcule a velocidade angular correspondente de cada um.
19. Um bloco é comprimido contra uma mola, desde sua posição de equilíbrio para outra posição e posteriormente é solto. Considere o sistema bloco-mola livre de forças dissipativas e que o bloco entra em m.h.s com período igual a $T =4\,s$. Determine a frequência do movimento, a pulsação e a fase inicial.
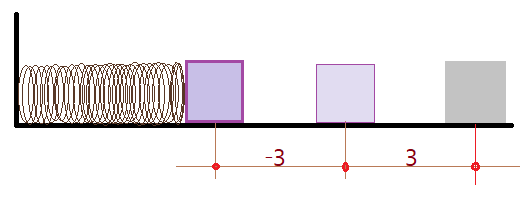
20. Um bloco de massa 500 g está preso a uma mola de constante elástica , formando um sistema massa-mola como o da Figura 1. O bloco então é puxado por uma superfície sem atrito até uma distância de 10 cm a partir da posição de equilíbrio (x = 0) e é liberado no instante $t =0$. Com base nestas informações calcule:
a) A frequência angular, a frequência e o período do movimento;
b) A aceleração máxima do bloco;
21. Em um sistema massa-mola, um bloco de massa $m = 20\,kg$, está preso a uma mola de constante elástica desconhecida, quando é solto, a uma distância de $A = 15\,cm$ da posição de equilíbrio a partir do repouso. Sabe-se que a frequência das oscilações do sistema é de $f = 1,51\,Hz$. Com base nestas informações calcule:
a)o período de oscilação do sistema;
b)a pulsação do oscilador;
c)a velocidade ao passar pela posição de equilíbrio;
d)o ângulo de fase no instante $t = 3\,s$.
22. Uma partícula de massa $m =2\,kg$, presa a um fio inextensível de comprimento $L = 2\,m$, oscila de modo a formar um pêndulo simples. Considere $g = 9,8\,m/s^{2}$ e calcule:
a) O período das oscilações;
b) a tensão no fio quando a partícula passa pelo ponto mais baixo da trajetória;
Havendo dúvidas, mesmo que sejam de problemas encontrados em outras fontes, faça contato para esclarecer e receber ajuda em suas dificuldades.
Curitiba, 13 de maio de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
