Física – Mecânica, Energia
O que é energia?
Energia é a capacidade de realizar trabalho.
É uma forma bem simples e resumida de expressar a ideia do que vem a ser a tal Energia.
Quando estudamos Trabalho, (Lembra-se?) vimos que o trabalho é realizado por uma força que realiza um deslocamento. Para produzir força, há necessidade de energia. Isso estabelece a conexão entre trabalho e energia.
O trabalho é o processo de transformar determinada forma energia, que pode estar armazenada, em outra. É possível estabelecer uma longa cadeia dessas transformações sucessivas de uma energia em outra, sempre pela realização de trabalho. Esse trabalho pode resultar em um produto, destinado ao comércio de consumo ou de utilização em diferentes atividades humanas.
Energia mecânica
É a energia que envolve movimento ou possibilidade de movimento. Ela se apresenta em dois estados: Energia potencial e Energia cinética.
A energia potencial depende da posição do corpo e a energia cinética depende da velocidade dele.
Se um corpo de massa $m$ está colocado a uma altura $h$ em relação a um referencial fixo no solo, ele terá a capacidade de deslocar-se da posição $y_{0} = h$ até a posição $y = 0$, no referido referencial. Vimos que a velocidade do corpo em queda cresce na medida que ele se desloca para baixo.
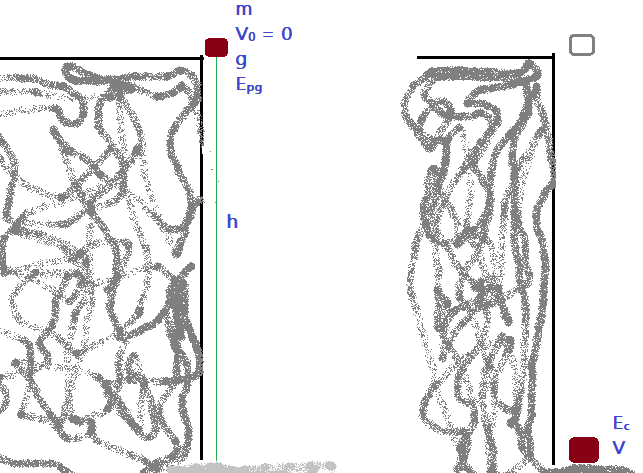
Energia potencial gravitacional
Observemos a figura acima. O corpo de massa $m$, cai da altura $h$. Na posição inicial ele está provido de energia cinética igual a zero e energia potencial gravitacional, que o fará deslocar-se até o solo, realizando um trabalho dado pela expressão:
$\tau = P\times h$$\Leftrightarrow$$\tau = m\times g\times h$
Esse trabalho é a transformação da energia potencial gravitacional em energia cinética e por isso podemos dizer que a energia potencial gravitacional inicial é:
$$\color{Brwon}{E_{pg} = m\times g\times h}$$
Energia cinética
Durante a queda a energia potencial é convertida em energia cinética, até chegar ao solo. Usando a equação de Torricelli para o movimento de queda livre, temos:
$v^{2} = v_{0}^{2} + 2\times g\times h$$\Leftrightarrow$$\frac{v^{2}}{2}= gh$
$E_{c} = E_{pg} = mgh$
Substituindo $gh$ por $\frac{v^{2}}{2}$, teremos:
$E_{c}= \frac{1}{2}\times m\times v^{2}$
Temos pois: $$\color{Brown}{E_{pg}= m g h}$$
$$\color{Brown}{E_{c} = \frac{1}{2} m v^{2}}$$
Unidades de energia:
Energia e trabalho são grandezas de mesma natureza e por isso são medidas nas mesmas unidades. Assim:
a) No SI: a unidade é o joule (J), ou $N/m$
b) No MKgfS ou sistema técnico métrico: quilogrâmetro(kgm).
c) No sistema CGS, medimos energia e trabalho em: erg.
Conversões:
$1\,J = 1\, N\cdot 1\, m$$\Leftrightarrow$$1\, J = 10^{5}\,dyn\cdot 10^{2}\, cm = 10^{7}\, erg$
$$\color{Brown}{1\, J = 10^{7}\, erg}$$
$1kgm = 1\,kgf\times 1\, m$$\Leftrightarrow$$ 1\,kgm = 9,8 N\times 1\, m = 9,8\,J$
$$\color{Brown}{1\,kgm = 9,8\, J}$$
Durante o percurso da altura $h$, a cada instante diminui a energia potencial gravitacional e aumenta na mesma proporção a energia cinética. Isso permite afirmar que, em qualquer ponto da queda, a energia mecânica total do corpo é a soma da energia potencial remanescente e da energia cinética acumulada. Assim:
$$\color{Blue}{E_{c} + E_{pg} = E_{m}}$$
Conservação da energia
Se a experiência for realizada em condições consideradas conservativas, isto é, não há perda de energia por atrito, resistência do ar ou outra forma de energia dissipativa, a energia mecânica se conserva, ou seja, permanece constante.
Podemos dizer que se o sistema de forças for conservativo, a energia mecânica se conserva. Um sistema é considerado conservativo se não houver dissipação de energia no ambiente, para outras formas como calor, ruído e etc.
Como exemplos de forças conservativas podemos citar as gravitacionais, as elásticas dentro de certos limites e algumas outras formas que iremos ver no decorrer dos assuntos vindouros.
Vamos exercitar um pouco
01. Uma pedra de forma esférica, tendo massa de $\color{Sepia}{m = 5,0\, kg}$, cai do alto de uma torre de altura iguala $\color{Sepia}{h= 20,0\, m}$. Sendo a aceleração da gravidade local igual a $\color{Sepia}{g=10,0\,m/ s^{2}}$, determine: a) a energia potencial no início do movimento; b) a velocidade da pedra quando metade de sua energia potencial estiver transformada em cinética; c) a energia cinética no instante que antecede o impacto com o chão; d) a pedra gasta uma fração de $\color{Sepia}{t = 0,25\,s}$ para parar, ficando incrustada no chão. Qual foi seu impulso e a intensidade da força média que atuou sobre ela até parar.
a) $\color{Blue}{E_{pg} = m\times g\times h}$
$E_{pg} = 5,0\times 10,0\times 20,0$$\Leftrightarrow$$E_{pg}= 1000,0 \,J$
$$\color{Brown}{E_{pg}= 10^{3}\,J}$$
b)$E_{c} = \frac{m\times g\times h}{2}$$\Leftrightarrow$$E_{c}= \frac{10^{3}}{2}$
$E_{c} = \frac{1}{2}\times m\times {v^{2}}$$\Leftrightarrow$$\frac{1}{\not{2}}\times {5,0}\times {v^{2}} = \frac{5\times 10^{2}}{\not{2}}$
$V^{2} = \frac{5\cdot 10^{2}}{5,0} = 100,0$$\Leftrightarrow$$\sqrt{v^{2}} = \sqrt{100}$
$$\color{Brown}{V = {10,0}\, m/s}$$
c) no instante que irá ocorrer o impacto a energia potencial estará totalmente convertida em cinética. Assim:
$E_{c} + E_{pg} = {10^{3}}$$\Leftrightarrow$$\color{Brown}{E_{c} + 0 = {10,0}^{3}\, J}$
d) o impulso é igual a variação da quantidade de movimento. Calculemos a velocidade nesse instante do impacto.
$E_{c}= \frac{m\times v^{2}}{2}$$\Leftrightarrow$$ {10,0}^{3} = \frac{{5,0}\times v^{2}}{2}$
$v^{2}= \frac{10^{3}\times 2}{5,0}$$\Leftrightarrow$$\sqrt{V^{2}} = \sqrt{400}$
$$\color{Brown}{V = {20,0}\, m/s}$$
$I = m\times {\Delta V}= m\times(V – V_{0})$$\Leftrightarrow$$ I = {5,0}\times{0 – 20,0}$
$F\times\Delta t = – 1000,0$$\Leftrightarrow$$F = \frac{-1000,0}{0,25}= – 4000\, N$
$$\color{Brown}{F = – {4000,0}\, N}$$
A força média será de $F = {- 4000,0}\, N$, em sentido oposto ao do movimento.
02. Um bloco de pedra, de $\color{Sepia}{m = 400\, kg}$, desce um plano inclinado a partir do repouso, deslizando sobre rolos de madeira, sem atrito.
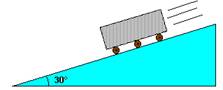
Sabendo-se que o plano inclinado mede $\color{Sepia}{\Delta x =12,0 \,m}$ e sua inclinação é de $\color{Sepia}{\theta =30^{0}}$ em relação à horizontal, calcule o trabalho resultante das forças que atuam no bloco. Considere a gravidade $\color{Sepia}{g = 10,0 m/s^{2}}$.
A força peso pode ser decomposta em duas componentes. Uma é normal ao plano e a outra é paralela ao plano. Sendo o deslocamento paralelo ao plano, a força normal não realiza trabalho. Ficamos com a componente paralela ao plano para realizar o trabalho de deslocar o bloco até o ponto mais baixo.
$$\color{Blue}{P_{x} = P. sen(30^{0})}$$
$\tau = P_{x}\times 12$$\Leftrightarrow$$\tau = m\times g\times sen(30^{0})\times 12$
$\tau = 400\times{10,0}\times {12}\times \frac{1}{2}$
$\tau = {4000,0}\times{12}\frac{1}{2}$$\Leftrightarrow$$\tau = 24000,0 J$
$$\color{Brown}{\tau = 24000,0\, J}$$
03. Uma esfera de $\color{Sepia}{m = 2,0\, kg}$ é lançada de uma altura $\color{Sepia}{y_{0} =12,0\, m}$, com velocidade vertical dirigida para cima $\color{Sepia}{v_{0}=20,0\, m/s}$, em um local onde $\color{Sepia}{g = 10,0 m/s^{2}}$. Determine: a) a energia potencial gravitacional inicial; b) a energia cinética inicial; c) a altura máxima atingida e sua energia potencial nesse instante; d) o tempo gasto no movimento de subida; e) o tempo total decorrido entre o lançamento e o impacto no solo; f) a velocidade no instante anterior ao impacto no solo.
a) $\color{Blue}{E_{pg}= m\times g\times h}$
$E_{pg}= 2,0\times 10,0\times 12,0$$\Leftrightarrow$$E_{pg}= 240,0\,J$
$$\color{Brown}{E_{pg}= 240,0\,J}$$
b)$E_{co} = \frac{1}{2}\times m\times v^{2}$
$E_{co}= \frac{1}{2}\cdot 2,0\times {(20,0)}^{2}$$\Leftrightarrow$$E_{co}=\frac{1}{2}\times {800,0} = 400\, J$
$$\color{Brown}{E_{co}= 400,0\,J}$$
c) Na altura máxima, a velocidade se torna nula. Por isso:
$$v^{2} = v_{0}^{2} – 2\times g\times\Delta y$$
$ 0 = {20,0}^{2} – 2\times 10,0\times {y-y_{0}}$
$y – 12,0 = \frac{400,0}{20,0}\,$$\Leftrightarrow$$ y = 20,0 + 12,0 = 32,0\,m$
$$\color{Blue}{E_{p} = mgy }$$
$E_{p} = 2,0\times 10,0\times 32,0 =640,0 \, J$
$$\color{Brown}{E_{p}= 640,0\, J}$$
d) $\color{Blue}{v = v_{0} – g\times t}$
$ 0 = 20,0 – 10,0\times t$$\Leftrightarrow$$10\times t = 20,0$
$t = \frac{20,0}{10,0} = 2,0\, s$$\Leftrightarrow$$\color{Brown}{t = 2,0\, s}$
e)a equação do movimento vertical é:
$$y = y_{o} + v_{o} t + \frac{1}{2}\g t^{2}$$
$0 = 12 + 20 t – \frac{10}{2} t^{2}$$\Leftrightarrow$$5t^{2} – 20 t – 12 = 0$
Aplicando Baskahra:
$t= \frac{- b \pm\sqrt{b^{2} -4 a c}}{2 a}$$\Leftrightarrow$$ t = \frac{-{-20}\pm\sqrt{{-20}^{2} – 4\times 5\times{-12}}}{2\times5}$
$ = frac{20 \pm\sqrt{640}}{10}$
$t_{1} = \frac{20 + 8\sqrt{10}}{10}\simeq 4,53\,s$
$t_{2} = \frac{20 – 8\sqrt{10}}{10}\simes {-0,53\,s}\\not in R$
$$\color{Navy}{t \simeq 4,53\,s$$
f)$$\color{Blue}{v^{2} = v_{0}^{2} – 2\times g\times {(y- y_{0})}}$$
$v^2 = {20,0}^{2} – 2\times 10,0\times{(0 – 12)}$
$v^{2} = 400,0 – {(-240)} = 400,0 + 240$$\Leftrightarrow$$v^{2} = 640,0$
$\sqrt{v^{2}} = \sqrt{640,0}$$\Leftrightarrow$$V = 8\sqrt{10}$
$$\color{Brown}{v=8\sqrt{10}\, m/s}$$
04. Um carrinho de brinquedo, tem massa $\color{Sepia}{m=0,8\,kg}$ e se move sobre um plano horizontal com velocidade constante $\color{Sepia}{v = 3,0\,m/s}$. Aceitando que não há perda de energia por atrito ou outra força resistente, ele encontra pela frente uma rampa inclinada de $\color{Sepia}{\theta= 30^{0}}$, pede-se: a) qual é a sua energia cinética no plano horizontal; b) qual é a altura no instante em que ele para na subida da rampa; c) qual é a distância que ele subiu no plano inclinado?
a) $$\color{Blue}{E_{c} = \frac{m\times v^{2}}{2}}$$
$E_{c} = \frac{{0,8}\times {3,0}^{2}}{2}$$\Leftrightarrow$$E_{c} = \frac{7,2}{2} = 3,6\,J$
$$\color{Brown}{E_{c}= 3,6\,J}$$
b)$$\color{Blue}{E_{pg} = mgh}$$
$3,6 = 0,8\cdot\cdot 10\cdot h$$\Leftrightarrow$$h = \frac{3,6}{8} = 0,45\,m$
$$\color{Brown}{h = 0,45\,m}$$
c)O plano inclinado é a hipotenusa do triângulo formado e daí podemos estabelecer:
$$\color{Blue}{tg(30^{0}) = \frac{h}{\Delta X}}$$
$\frac{\sqrt{3}}{3} = \frac{h}{\Delta X}$$\Leftrightarrow$$\Delta X = \frac{h}{\frac{\sqrt{3}}{3}}$
$\Delta X = \frac{0,45\times 3}{\sqrt{3}}$$\Leftrightarrow$$\Delta X = \frac{1,35}{\sqrt{3}}$
$\Delta X = \frac{1,35\times \sqrt{3}}{\sqrt{3}^{2}}$
$\Delta X = \frac{1,35\sqrt{3}}{3} = {0,45}\times \sqrt{3}$$\Leftrightarrow$$\color{Brown}{\Delta X = 0,78 m}$
Energia potencial elástica
É a energia que um corpo acumula ao ser submetido a uma deformação elástica. A situação mais costumeira é a de uma mola helicoidal, submetida à tração ou compressão. Para provocar a deformação, precisamos de uma força que consome energia. Essa energia despendida pela força, é acumulada na elasticidade da mola. Ao cessar a ação da força a mola retorna ao tamanho original, devolvendo a energia acumulada. Vejamos as figuras.
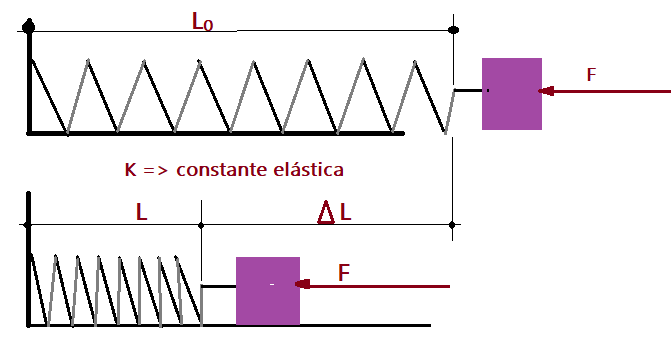
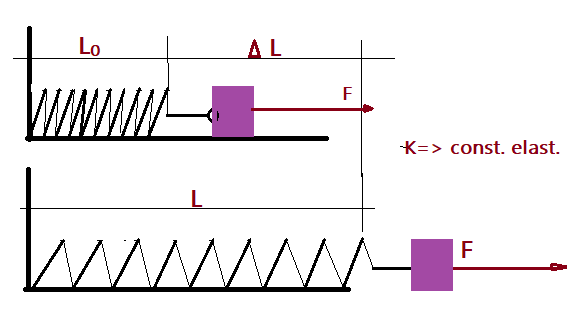
Lembrando das deformações elásticas, temos que:
$$\color{Blue}{F = k\times\Delta L}$$
Quando iniciamos a deformação, a força é portanto nula e seu valor cresce na medida em que a deformação aumenta. Isso nos leva a escrever a expressão do trabalho da força:
$\tau = \frac{{F + F_{0}}\times \Delta L}{2}$$\Leftrightarrow$$\tau = \frac{F\times \Delta L}{2}$
Substituindo a força pela expressão acima lembrada:
$\tau = \frac{{k\times\Delta L}\times \Delta L}{2}$$\Leftrightarrow$$\tau = \frac{k\times\Delta L^{2}}{2}$
Como o trabalho é conversão de uma forma de energia em outra, o que realizamos sobre a mola, transforma-se em energia potencial elástica.
$$\color{Brown}{E_{pe} = \frac{1}{2}\times k\times \Delta L^2}$$
Exercitando
01. Um bloco de pedra tem massa $\color{Sepia}{m = 20,0\,kg}$, colocado sobre roletes de madeira, tem velocidade $\color{Sepia}{v = 10,0\,m/s}$. Em seu caminho encontra uma mola horizontal, com constante elástica igual a $\color{Sepia}{k = 500\,N/m}$. Determine a deformação da mola no momento em que o corpo para?
A energia cinética do bloco irá ser convertida em energia potencial elástica da mola.
$$\color{Blue}{E_{pe} = E_{c}}$$
$\frac{1}{2}\times k\times {\Delta L}^{2}= \frac{1}{2}\times m\times v^{2}$
$ k\times {\Delta L}^{2} = 20,0\times {10,0}^{2}$
${500,0}\times \Delta L^{2} = 20,0\times {100,0}$$\Leftrightarrow$$\Delta L^{2} = \frac{2000,0}{500,0}$
$\Delta L^{2} = 4,0$$\Leftrightarrow$$\sqrt{\Delta L^{2}}= \sqrt{4,0}$
$\Delta L = \sqrt{4,0}$$\Leftrightarrow$$\Delta L =2,0$
$$\color{Brown}{\Delta L = 2,0\, m}$$
02. Uma mola de constante elástica $\color{Sepia}{k=300,0\,N/m}$, está fixada verticalmente e sobre ela, que está deformada de $\color{Sepia}{\Delta L = 30,0\,cm}$, e um bloco metálico de $\color{Sepia}{m = 0,40\,kg}$, está apoiado sobre ela. A aceleração da gravidade $\color{Sepia}{g =10,0\,m/s^{2}}$ e a mola está travada. No instante que ocorre o destravamento a mola se distende, lançando o bloco verticalmente para cima. Determine a altura atingida pelo bloco até que sua velocidade se anule.
A energia potencial elástica se transforma em energia cinética e imediatamente após em energia potencial gravitacional na medida que a altura aumenta. Na altura máxima, teremos a igualdade entre estas formas de energia.
$$\color{Blue}{E_{pg}= E_{pe}}$$
$mgh = \frac{1}{2}\times k\times \Delta L^{2}$$\Leftrightarrow$$0,40\times 10,0\times h = \frac{1}{2}{300,0}\times {(0,30)}^{2}$
$$\color{Brown}{h = \frac{27,0}{4,0} = 6,75\, m}$$
03. Uma mola está disposta na vertical, fixa no teto de uma sala. Sua constante elástica é $\color{Sepia}{k = 200,0\,N/m}$ e dispõe de um pequeno suporte na extremidade, onde se coloca um bloco de concreto de $\color{Sepia}{m = 4,0\,kg}$. Ao soltar o bloco, ele deforma a mola até que a força elástica iguala o peso. Enquanto isso o corpo acelera, distendendo a mola. Sendo $\color{Sepia}{g=10,0\,m/s^{2}}$, qual será a deformação da mola até que o bloco atinja a velocidade final nula. Qual é a deformação máxima da mola? O que irá ocorrer com o corpo depois desse instante? Se a mola for ideal e não existir resistência do ar, o movimento que se estabelece é de que tipo?
No instante em que a força elástica iguala o peso do corpo, teremos uma deformação e começa a desacelerar até parar.
$$\color{Blue}{P = F_{e}}$$
$m\times g = k\times \Delta L$$\Leftrightarrow$$\Delta L = \frac{m\times g}{k}$
$\Delta L = \frac{4,0\times 10,0}{200,0}$$\Leftrightarrow$$\Delta L = 0,20\, m$
Até este ponto o corpo transferiu energia potencial gravitacional para a mola que daí para frente começa o processo inverso.
A deformação máxima da mola será então igual ao dobro da que equilibra o peso.
$$\color{Blue}{\Delta L_{1} = 2\times {0,2} = 0,40 m}$$
Quando o corpo para, a ação da mola começa a fazer com que ele comece a subir recuperando a energia potencial e a mola perdendo a sua energia. Dessa forma, não havendo perdas pela resistência do ar e sendo uma mola ideal, o corpo fica executando um movimento oscilatório. Teremos um sistema massa-mola.
Exercícios para você treinar o taco.
01. Uma maçã presa em uma macieira a $\color{Sepia}{h = 3\,m}$ de altura se desprende. Com que velocidade ela chegará ao solo? Use a energia mecânica.
02. Um bloco de massa igual a $\color{Sepia}{m =10,0\,kg}$ se desloca com velocidade constante igual a $\\color{Sepia}{V =12,0\,m/s}$, ao encontrar uma mola de constante elástica igual a $\color{Sepia}{k =2000\,N/m}$ este diminui sua velocidade até parar, qual a compressão na mola neste momento?
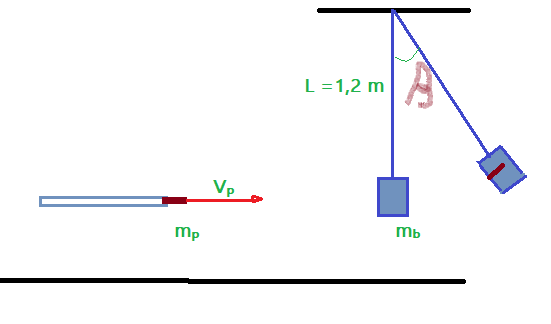
03. Um projétil de $\color{Sepia}{m_{p} = 30,0\,g}$ é disparado por uma arma que lhe imprime uma velocidade de saída de $\color{Sepia}{v_{p}= 900,0\,m/s}$. Movendo-se horizontalmente ela atinge alguns instantes depois do disparo um bloco de madeira de massa $\color{Sepia}{m_{b}= 5,0\,kg}$, suspenso por um cabo inextensível e flexível de $\color{Sepia}{L_{c}= 1,2\,m}$ de comprimento. Nele se incrusta e o conjunto oscila elevando-se até um ponto máximo. Determine o ângulo formado pelo cabo com a vertical na posição final do conjunto. Considere $\color{Sepia}{g = 10,0\,m/s^{2}}$.
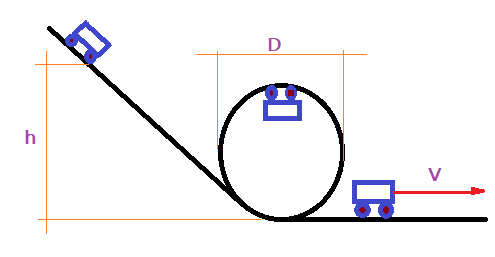
04. Um carrinho com rodas perfeitamente lubrificadas, tem massa $\color{Sepia}{m = 2,0\, kg}$, desce um trilho inclinado e percorre um loop circular antes de se deslocar no trecho horizontal. Supondo que $\color{Sepia}{g = 10,0\, m/s{2}}$, qual deve ser a altura mínima de onde o carrinho pode descer, percorrer o loop em segurança, sem o risco de perder contato com o trilho. O diâmetro do loop é de $\color{Sepia}{D = 0,80\,m}$.
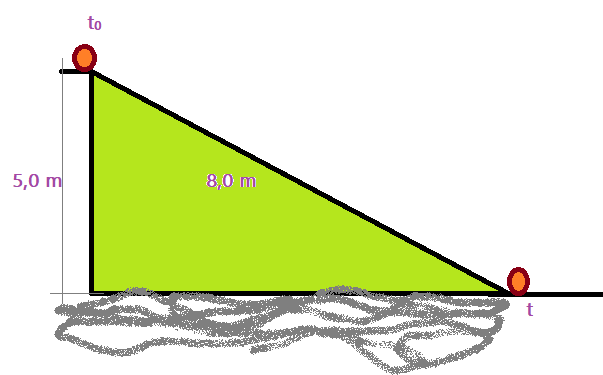
05. (G1 – IFBA) Um corpo é abandonado do alto de um plano inclinado, conforme a figura abaixo. Considerando as superfícies polidas ideais, a resistência do ar nula e $\color{Sepia}{g=10,0\,m/s^{2}}$como a aceleração da gravidade local, determine o valor aproximado da velocidade com que o corpo atinge o solo.
06. (UEG) – Em um experimento que valida a conservação da energia mecânica, um objeto de $\color{Sepia}{m = 4,0\,kg}$ colide horizontalmente com uma mola relaxada, de constante elástica de $\color{Sepia}{k =100,0\, N/m}$. Esse choque a comprime $\color{Sepia}{\Delta L =1,6\,cm}$. Qual é a velocidade, em $m/s$ desse objeto, antes de se chocar com a mola?
07. (G1 – IFSP) – Um atleta de salto com vara, durante sua corrida para transpor o obstáculo a sua frente, transforma a sua energia ………………….. em energia …………………….. devido ao ganho de altura e consequentemente ao/à ………………….. de sua velocidade.
As lacunas do texto acima são, correta e respectivamente, preenchidas por:
( )a) potencial – cinética – aumento;
( )b) térmica – potencial – diminuição;
( )c) cinética – potencial – diminuição;
( )d) cinética – térmica – aumento;
( )e) térmica – cinética – aumento.
08. Um corpo é solto a partir do repouso de uma rampa a uma altura de $\color{Sepia}{h_{1} = 4,0\,m}$. Determine a velocidade em que o corpo estará quando estiver a uma altura de $\color{Sepia}{h_{2}= 2,0\,m}$ do solo e indique a alternativa correta.
( )a) $2\sqrt{10}\,m/s$;
( )b) $20\,m/s$;
( )c) $4\sqrt{10}\,m/s$;
( )d) $2\sqrt{5}\,m/s$;
( )e) $3\sqrt{2}\,m/s$.
09. Um corpo de massa $\color{Sepia}{m = 2,0\,kg}$ encontra-se encostado em uma mola de constante elástica igual a $\color{Sepia}{k=5000\,N/m}$, comprimida em $\color{Sepia}{\Delta L =2,0\,cm}$. Desprezando-se as forças dissipativas e determine a altura atingida pelo corpo depois que a mola for liberada e assinale a alternativa correta.
(Dados: $\color{Sepia}{g = 10\,m/s^{2}}$)
( )a) $4\,cm$;
( )b) $10\,cm$;
( )c) $5\,cm$;
( )d) $20\,cm$;
( )e) $2\,cm$.
10. Vamos supor que um carrinho de montanha-russa esteja parado a uma altura igual a $\color{Sepia}{h = 10,0\,m}$ em relação ao solo. Calcule a velocidade do carrinho, nas unidades do SI, ao passar pelo ponto mais baixo da montanha-russa. Despreze as resistências e adote a massa do carrinho igual a $\color{Sepia}{m = 200\,kg}$.
( )a) $v\simeq 1,41\,m/s$;
( )b) $v\simeq 28\,m/s$;
( )c) $v\simeq 41\,m/s$;
( )d) $v\simeq 5,61\,m/s$;
( )e) $v\simeq 14,1\,m/s$.
11. Um corpo de massa $\color{Sepia}{m = 2,0\,kg}$ encontra-se encostado em uma mola de constante elástica igual a $\color{Sepia}{5000\,N/m}$, comprimida em $\color{Sepia}{2\,cm}$. Desprezando-se as forças dissipativas e com base na figura, determine a altura atingida pelo corpo depois que a mola for liberada e assinale a alternativa correta.
(Dados: $\color{Sepia}{g = 10\,m/s^{2}}$)
( )a) 4 cm;
( )b) 10 cm;
( )c) 5 cm;
( )d) 20 cm;
( )e) 2 cm.
12. Um corpo é solto a partir do repouso de uma rampa a uma altura de $\color{Sepia}{4\,m}$. Determine a velocidade em que o corpo estará quando estiver a uma altura de $\color{Sepia}{2\,m}$ do solo e indique a alternativa correta.
( )a)$2\sqrt{10}\,m/s$;
( )b)$20\,m/s$;
( )c)$4\sqrt{10}\,m/s$;
( )d)$2\sqrt{5}\,m/s$;
( )e)$3\sqrt{2}\,m/s$.
13. O conceito de energia foi de suma importância para o desenvolvimento da ciência, em particular da física. Sendo assim, podemos dizer que o princípio da conservação da energia mecânica diz que:
( )a) nada se perde, nada se cria, tudo se transforma;
( )b) que a energia pode ser gastada e perdida;
( )c) a energia total de um sistema isolado é constante;
( )d) que a energia jamais pode ser transferida de um corpo a outro;
( )e) a energia cinética de um corpo está relacionada com a força da gravidade.
14. Imagine que você deixa cair (abandonado) um objeto de massa m e de altura de 51,2 metros. Determine a velocidade desse objeto ao tocar o solo.
( )a) $v = 50\, m/s$;
( )b) $v = 40\,m/s$;
( )c) $v = 32\,m/s$;
( )d) $v = 20\,m/s$;
( )e) $v = 10\,m/s$.
15. Vamos supor que um carrinho de montanha-russa esteja parado a uma altura igual a $\color{Sepia}{10\,m}$ em relação ao solo. Calcule a velocidade do carrinho, nas unidades do SI, ao passar pelo ponto mais baixo da montanha-russa. Despreze as resistências e adote a massa do carrinho igual a $\color{Sepia}{200\,kg}$.
( )a) $v\simeq 1,41\,m/s$;
( )b) $v\simeq 28\,m/s$;
( )c) $v\simeq 41\,m/s$;
( )d) $v\simeq 5,61\,m/s$;
( )e) $v\simeq 14,1\,m/s$.
16. Determine o valor da velocidade de um objeto de $\color{Sepia}{0,5\,kg}$ que cai, a partir do repouso, de uma altura igual a $\color{Sepia}{ 5\,m}$ do solo.
( )a) $v_{b} = 30\,m/s$;
( )b) $v_{b}= 10\,m/s$;
( )c) $v_{b}= 20\,m/s$;
( )d) $v_{b}= 0,5\,m/s$;
( )e) $v_{b}=0$.
17. Uma maçã presa em uma macieira a$\color{Sepia}{3\,m}$ de altura se desprende. Com que velocidade ela chegará ao solo? Dado:$\color{Sepia}{g=10\,m/s^{2}}$.
18. Um bloco de massa igual a $\color{Sepia}{10\,kg}$ se desloca com velocidade constante igual a $\color{Sepia}{12\,m/s}$, ao encontrar uma mola de constante elástica igual a $\color{sepia}{k= 2000\,N/m}$ este diminui sua velocidade até parar, qual a compressão na mola neste momento?
19. (G1 – IFBA) – Um corpo é abandonado do alto de um plano inclinado, conforme a figura abaixo. Considerando as superfícies polidas ideais, a resistência do ar nula e $\color{Sepia}{10\,m/s^{2}}$ como a aceleração da gravidade local, determine o valor aproximado da velocidade com que o corpo atinge o solo:
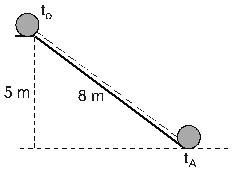
( )a) $v = 84\,m/s$;
( )b) $v = 45\,m/s$;
( )c) $v = 25\,m/s$;
( )d) $v = 10\,m/s$;
( )e) $v = 5\,m/s$.
20. (UEG) – Em um experimento que valida a conservação da energia mecânica, um objeto de $\color{Sepia}{4,0\,kg}$ colide horizontalmente com uma mola relaxada, de constante elástica de $\color{Sepia}{100\,N/}$m. Esse choque a comprime $\color{Sepia}{\Delta x =1,6\,cm}$. Qual é a velocidade, em m/s desse objeto, antes de se chocar com a mola?
( )a) 0,02;
( )b) 0,40;
( )c) 0,08;
( )d) 0,13;
( )e) 0,17.
21. (IFSC) – O bate-estacas é um dispositivo muito utilizado na fase inicial de uma construção. Ele é responsável pela colocação das estacas, na maioria das vezes de concreto, que fazem parte da fundação de um prédio, por exemplo. O funcionamento dele é relativamente simples: um motor suspende, através de um cabo de aço, um enorme peso (martelo), que é abandonado de uma altura, por exemplo, de $\color{Sepia}{h = 10\,m}$, e que acaba atingindo a estaca de concreto que se encontra logo abaixo. O processo de suspensão e abandono do peso sobre a estaca continua até a estaca estar na posição desejada.
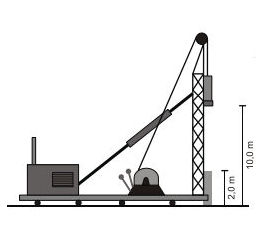
É CORRETO afirmar que o funcionamento do bate-estacas é baseado no princípio de:
( )a) transformação da energia mecânica do martelo em energia térmica da estaca;
( )b) conservação da quantidade de movimento do martelo;
( )c) transformação da energia potencial gravitacional em trabalho para empurrar a estaca;
( )d) colisões do tipo elástico entre o martelo e a estaca;
( )e) transformação da energia elétrica do motor em energia potencial elástica do martelo.
22. (UNESP) – A figura ilustra um brinquedo oferecido por alguns parques, conhecido por tirolesa, no qual uma pessoa desce de determinada altura segurando-se em uma roldana apoiada numa corda tensionada. Em determinado ponto do percurso, a pessoa se solta e cai na água de um lago.
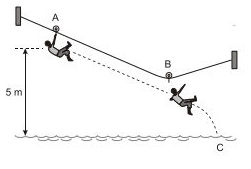
Considere que uma pessoa de $\color{sepia}{50\,kg}$ parta do repouso no ponto A e desça até o ponto B segurando-se na roldana, e que nesse trajeto tenha havido perda de $\color{Sepia}{36\%}$ da energia mecânica do sistema, devido ao atrito entre a roldana e a corda. No ponto B ela se solta, atingindo o ponto C na superfície da água. Em seu movimento, o centro de massa da pessoa sofre o desnível vertical de 5 m mostrado na figura. Desprezando a resistência do ar e a massa da roldana, e adotando $\color{Sepia}{g = 10\,m/s^{2}}$, pode-se afirmar que a pessoa atinge o ponto C com uma velocidade, em m/s, de módulo igual a:
( )a) 8;
( )b) 10;
( )c) 6;
( )d) 12;
( )e) 4.
23. (UEM-2012/Adaptada) – Segue abaixo algumas questões que envolvem a energia mecânica e a conservação de energia. De tal modo, assinale a alternativa incorreta.
( )a) Denomina-se energia cinética a energia que um corpo possui, por este estar em movimento;
( )b) Pode-se denominar de energia potencial gravitacional a energia que um corpo possui por se situar a uma certa altura acima da superfície terrestre;
( )c) A energia mecânica total de um corpo é conservada, mesmo com a ocorrência de atrito;
( )d) A energia total do universo é sempre constante, podendo ser transformada de uma forma para outra; entretanto, não pode ser criada e nem destruída;
( )e) Quando um corpo possui energia cinética, ele é capaz de realizar trabalho.
24. (UFSM-2013) Um ônibus de massa m anda por uma estrada de montanha e desce uma altura h. O motorista mantém os freios acionados, de modo que a velocidade é mantida constante em módulo durante todo o trajeto. Considerando as afirmativas a seguir, assinale se são verdadeiras (V) ou falsas (F).
( ) A variação da energia cinética do ônibus é nula.
( ) A energia mecânica do sistema ônibus-Terra se conserva, pois a velocidade do ônibus é constante.
( ) A energia total do sistema ônibus-Terra se conserva, embora parte da energia mecânica se transforme em energia interna.
A sequência correta é:
( )a) V, V, F;
( )b) V, F, V;
( )c) F, F, V;
( )d) V, V, V:
( )e) F, F, V.
25. (Enem-2012) – Os carrinhos de brinquedo podem ser de vários tipos. Dentre eles, há os movidos a corda, em que uma mola em seu interior é comprimida quando a criança puxa o carrinho para trás. Ao ser solto, o carrinho entra em movimento enquanto a mola volta à sua forma inicial. O processo de conversão de energia que ocorre no carrinho descrito também é verificado em:
( )a) um dínamo;
( )b) um freio de automóvel;
( )c) um motor a combustão;
( )d) uma usina hidroelétrica;
( )e) uma atiradeira (estilingue).
26. Uma bolinha de $\color{Sepia}{m =2\,kg}$ é abandonada a uma altura de $\color{Sepia}{h = 5\,m}$. Desprezando a resistência do ar, responda as perguntas abaixo:
A) Qual a variação de energia cinética da bolinha do instante inicial até o momento em que toca no solo?
B) Qual a velocidade final da bolinha?
27. Uma bolinha de massa $\color{Sepia}{80\,g}$ é arremessada do solo e alcança uma altura de $\color{Sepia}{h =5\,m}$, em relação ao solo. Qual foi a sua variação de energia potencial gravitacional?
28. Um bloco de massa m parte do repouso a uma altura $h_{o}$ em relação ao solo. Ao final do movimento irá colidir com uma mola de constante elástica $k$. Qual será a máxima deformação sofrida pela mola?
29. Um guindaste faz com que um corpo de massa 1,0 tonelada suba uma altura de 2,4 m em 2 minutos, com velocidade constante. Qual a potência do motor (ideal) do guindaste?
30. Qual o trabalho realizado por um corpo de massa $\color{Sepia}{m = 10\,kg}$, que inicia um percurso com velocidade $\color{Sepia}{v_{o} = 10m/s^{2}}$ até parar?
Havendo dúvidas consulte-me para poder esclarecer tudo.
Curitiba, 03 de maio de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
