Física – Mecânica, Cinemática. Movimento circular.
Movimento circular
O movimento circular se caracteriza por ocorrer em uma trajetória circular. Ele pode ocorrer em sentido horário ou em sentido anti-horário. Isso não afeta as suas grandezas de modo geral. Ao tratarmos simultaneamente de dois movimentos, sendo um com sentido inverso do outro, consideraremos um (convenção livre) como positivo e o outro negativo.
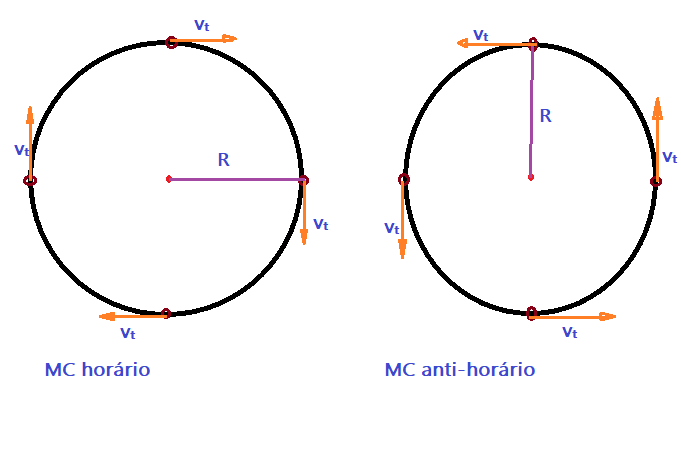
Nas duas figuras acima vemos a trajetória e os móveis em MC, no sentido horário e anti-horário. Podemos avaliar a rapidez do móvel partindo de duas grandezas representativas da posição. Uma é chamada de velocidade tangencial e a outra de velocidade angular.
Observando as figuras acima, vemos que os móveis ocupam em momentos sucessivos as mesmas posições anteriores, repetindo-se isso de modo “periódico”. Por tal motivo esses movimentos são denominados periódicos. O tempo transcorrido entre uma passagem por um ponto e a seguinte é o período:
Período é o tempo gasto pelo móvel em movimento circular entre duas passagens consecutivas pela mesma posição da trajetória.
Unidade: em qualquer sistema o período é geralmente medido em segundos. $$\color{Brown}{T = s}$$
Frequência: é a grandeza inversa do período.
$$\color{Brown}{f= \frac{1}{T}}$$
Unidade: a unidade de frequência é hertz (Hz)
A unidade de frequência foi batizada com esse nome em homenagem a um físico alemão, autor de pesquisas importantes sobre os movimentos periódicos, de nome Gustav Hertz.
Velocidade tangencial ou linear
No estudo da geometria, vimos que um círculo tem um perímetro ou o seu comprimento, dado pela expressão:
$$\color{Brown}{C = 2\cdot\pi\cdot R}$$
Se o móvel percorre a distância C no intervalo de tempo T, sua velocidade linear ou tangencial será:
$$V = \frac{C}{T}$$ $$V=\frac{2\cdot\pi\cdot R}{T}$$
Se a frequência é inversa do período, também podemos tomar o período como o inverso da frequência.
$$f = \frac{1}{T}$$ $$T = \frac{1}{f}$$
Em consequência podemos escrever as expressões da velocidade tangencial assim:
$$\color{Blue}{V = {C}\cdot\frac{1}{T} = C\cdot f}$$ $$\color{Blue}{V=2\cdot\pi\cdot R\cdot f}$$
As unidades para medir a velocidade seguem os critérios do sistema de unidades adotado em cada situação.
Velocidade angular
O raio do círculo, une o móvel ao centro e podemos medir os ângulos descritos nos intervalos de tempo decorridos. Assim, durante uma volta completa, isto é, durante um período de revolução, o móvel descreve um arco de:
$$\theta = 2\pi\, rad = 360^{0}$$
Isso nos diz que a velocidade angular é:
$$\color{Brown}{w = \frac{\theta}{T} = \frac{360^{0}}{T} = \frac{2\pi}{T}}$$
$$\color{Brown}{w = \theta\cdot f = 360^{0}\cdot f = 2\pi\cdot f}$$
Unidades: a velocidade angular será medida em $rad/s$ ou em $^{0}/s$.
Sabemos do estudo da geometria que, usando a unidade radiano para medir os ângulos, podemos determinar o comprimento do arco, multiplicando o raio pelo ângulo.
$$C_{\widehat{AB}}= \theta\cdot R$$
Pelo mesmo raciocínio podemos estabelecer uma relação entre a velocidade angular e a velocidade tangencial do móvel em movimento circular.
$$ V = 2\cdot\pi\cdot R\cdot\frac{1}{T}$$
$$w = 2\cdot\pi\cdot\frac{1}{T}$$
$$\color{Blue}{V = w\cdot R}$$
MCU-Movimento circular uniforme.
É o movimento circular em que a velocidade angular e a velocidade tangencial são constantes. Há porém um detalhe importante. No MCU existe uma aceleração, denominada aceleração centrípeta. Esse nome significa por sua origem “que busca o centro” ou “dirigida para o centro”. Essa aceleração é causada por uma força denominada força centrípeta. Essa força é normal (perpendicular) à velocidade tangencial e é dirigida para o centro do círculo na direção do raio.
Vamos ver como se chega à aceleração centrípeta. Vejamos o móvel nos pontos $A$ e $B$, sobre o círculo de raio $R$. A velocidade tangencial é constante em módulo, mas muda de direção a cada ponto que o móvel avança em seu movimento.
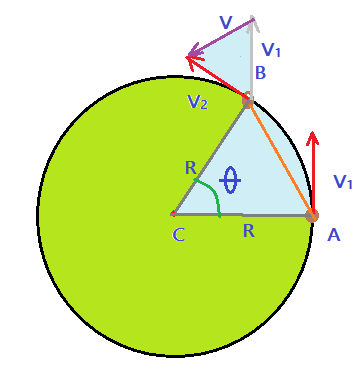
O móvel se desloca do ponto A para o ponto B, com velocidade de módulo constante. O deslocamento executa o arco $\widehat{AB}$, que subtende o ângulo $\theta$ e o arco de círculo $\overline{AB}$. Transportando o vetor velocidade $\vec{V_{1}}$, para a origem do vetor velocidade $\vec{V_{2}}$, formamos dois triângulos semelhantes. O $\Delta{ABCA}$ e o triângulo formado pelas velocidades, cujo terceiro lado $\Delta\vec{V}$ representa a variação vetorial da velocidade tangencial. $V_{1} = V_{2} = V$. Sendo os triângulos semelhantes, seus lados homólogos são proporcionais. Assim podemos escrever:
$\frac{|\Delta\vec{V}|}{\overline{AB}} = \frac{|\vec{V}|}{R}$
Nosso objetivo é determinar a aceleração centrípeta que age em um ponto, o que nos leva a estreitar o ângulo $\theta$ para um valor muito pequeno, próximo de zero. Nestas condições o segmento $\overline{AB}$ se iguala ao arco $\widehat{AB}$. O arco representa o deslocamento linear do móvel num intervalo de tempo $\Delta t$, de modo que:
$\widehat{AB} = V\cdot \Delta t$
$\frac{\Delta V}{V\cdot\Delta t} = \frac{V}{R}$
$\frac{\Delta V}{\Delta t} = \frac{V^{2}}{R}$
O primeiro membro dessa equação representa a aceleração vetorial do móvel. Sendo a única aceleração presente a centrípeta, podemos substituir esse membro por :
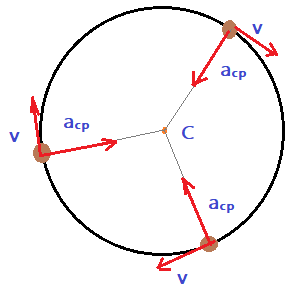
$$\color{Blue}{a_{cp}= \frac{v^{2}}{R}}$$
Substituindo $V = w\cdot R$
$a_{cp}=\frac{{w\cdot R}^{2}}{R}$
$a_{cp}= \frac{{w}^{2}\cdot {R}^{2}}{R}= {w}^{2}\cdot R$
$$\color{Blue}{a_{cp}= {w}^{2}\cdot R}$$
Equação horária angular
Podemos calcular a posição do móvel em seu MCU, com relação a denominada origem dos arcos, via de regra adotada no ponto em que o semi-eixo $\overrightarrow{OX}$, corta o círculo. É um bom momento para recordar essa parte do assunto estudado no círculo trigonométrico.
$$\color{Brown}{\theta = \theta_{0} + w\cdot t}$$
Essa equação identifica a posição do móvel sobre a trajetória circular, relativamente à origem dos arcos. Se adotarmos o sentido horário como o positivo e como negativo o sentido horário, a posição será estabelecida com relação a esse ponto.
Para melhor entender o mecanismo dos movimentos circulares, especialmente a questão da força centrípeta e aceleração centrípeta, é conveniente analisar a seguinte situação. Se fixarmos uma pedra ou uma esfera na extremidade de um cordão (barbante), fazendo-o girar, o objeto irá descrever um movimento circular. Digamos que o cordão arrebente ou seja solto num dado instante, o que irá acontecer com o objeto na ponta?
Para melhor entender o mecanismo dos movimentos circulares, especialmente a questão da força centrípeta e aceleração centrípeta, é conveniente analisar a seguinte situação. Se fixarmos uma pedra ou uma esfera na extremidade de um cordão (barbante), fazendo-o girar, o objeto irá descrever um movimento circular. Digamos que o cordão arrebente ou seja solto num dado instante, o que irá acontecer com o objeto na ponta?
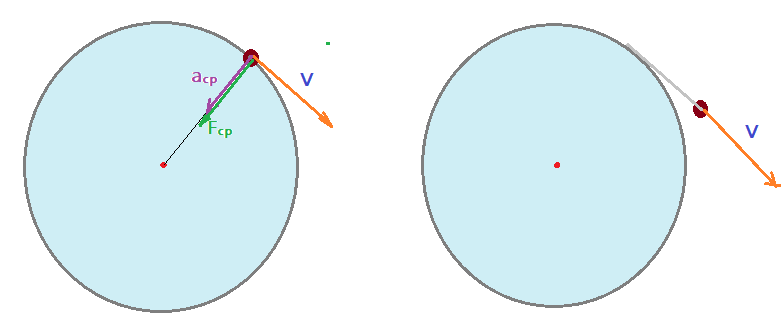
No instante que deixa de atuar a $F_{cp}$, responsável pela mudança da direção da velocidade tangencial em cada ponto, o corpo segue na mesma direção e fica sujeito apenas a outras forças existentes no local.
Movimento circular uniformemente variado.
Um objeto descreve um movimento circular uniformemente variado, se sua velocidade angular, bem como a tangencial, varia de valores iguais em intervalos de tempo iguais. Isto nos mostra que neste caso teremos, além da aceleração centrípeta a cada ponto, uma aceleração tangencial e outra angular.
Aceleração tangencial
Seja a velocidade tangencial no instante $t_{0}$ igual a $V_{0}$ e $V$ no instante $t$.
$a = \frac{\Delta V}{\Delta t}$$\Leftrightarrow$$a = \frac{V – V_{0}}{t -t_{0}}$
$$\color{Blue}{a = \frac{V – V_{0}}{t – t{0}}}$$
Habitualmente consideramos o tempo inicial igual a zero, e isso nos dá:
$a\cdot t = V – V_{0}$$\Leftrightarrow$$ V = V_{0} + a\cdot t$
$$\color{Blue}{V = V_{0} + a\cdot t}$$
Unidades:
1) No SI, a unidade será $m/s^{2}$, assim como no MKgfS.
2) No CGS, teremos $cm/s^{2}$.
Desse modo a velocidade tangencial em cada ponto será diferente não apenas em direção e sentido, como também em módulo. Se este aumentar, o movimento é acelerado e se diminuir o movimento será retaredado.
Aceleração angular:
Seja $w_{0}$ a velocidade angular no instante inicial $t_{0}= 0$ e $w$ no instante $t$, teremos uma aceleração angular dada por:
$\Omega = \frac{\Delta w}{\Delta t}$$\Leftrightarrow$$\Omega = \frac{w – w_{0}}{t}$
$\Omega\cdot t = w – w_{0}$$\Leftrightarrow$$w = w_{0} + \Omega\cdot t$
$$\color{Blue}{w = w_{0} + \Omega\cdot t}$$
Unidade: no SI será $rad/s^{2}$.
Equação horária angular no MCUV
$\color{Blue}{\theta = \theta_{0} + w_{0}\cdot t +\frac{\Omega\cdot t^{2}}{2}}$
Vamos aplicar o aprendido
01. Um móvel percorre uma circunferência de $R=2\, m$ com velocidade angular constante de $w=4\pi\, rad/s$. Determine:
- frequência;
- período;
- velocidade linear;
- qual ângulo, em graus, o móvel percorreu em 0,1 segundo;
- aceleração resultante nesse movimento.
A frequência podemos obter com a expressão $w = 2\pi\cdot f$
$4\pi = 2\pi\cdot f$$\Leftrightarrow$$f =\frac{4\pi}{2\pi}$
$$\color{Brown}{f = 2 Hz}$$
O período é inverso da frequência:
$$T = \frac{1}{f}$$
$T = \frac{1}{2}$$\Leftrightarrow$$\color{Brown}{T = 0,5\, s}$
A velocidade linear ou tangencial:
$$V = 2\cdot\pi\cdot R\cdot f$$
$V = 2\cdot\pi\cdot 2\cdot 2$$\Leftrightarrow$$\color{Brown}{V = 8\pi\, m/s}$
Ângulo descrito em $T = 0,1\, s$. Vamos converter a velocidade angular em $^0/s$.
$2\pi = 360^{0}$
$4\pi = x$
$x = \frac{4\cdot\pi\cdot(360^{0})}{2\cdot\pi}$$\Leftrightarrow$$ x = 720^{0}$
Se o móvel descreve um ângulo de $720^{0}$ em um segundo, significa que:
$\theta = w\cdot t$$\Leftrightarrow$$\theta = 720^{0}\cdot {0,1} = 72^{0}$
$$\color{Brown}{\theta = 72^{0}}$$
A aceleração é a centrípeta:
$a_{cp} = \frac{v^{2}}{R}$$\Leftrightarrow$$a_{cp}=\frac{(8\pi)^{2}}{2}$
$a_{cp}=\frac{64(\pi)^{2}}{2}$$\Leftrightarrow$$\color{Brown}{a_{cp}= 32\pi^{2} m/s^2}$.
02. (UFCE) – Um automóvel se desloca em uma estrada horizontal com velocidade constante de modo tal que os seus pneus rolam sem qualquer deslizamento na pista. Cada pneu tem diâmetro $D = 0,50\, m$, e um medidor colocado em um deles registra uma frequência de $f = 840\, rpm$. Qual é a velocidade do automóvel?
Vamos determinar a distância percorrida a cada volta do pneu.
$C = 2\pi\cdot R$
$C = 2\pi\cdot \frac{0,50}{2}$$\Leftrightarrow$$ C=\frac{\pi}{2}\, m$
Se $f = 840\, rpm$$\Rightarrow$$ f = \frac{840}{60} = 14 Hz$
$\color{Brown}{v = \frac{\pi}{2}\cdot f = \frac{\pi}{2}\cdot 14= 7\pi\, m/s}$
Se quisermos saber o valor da velocidade em $km/h$, usaremos uma regra de três.
$1 km/h = \frac{1}{3,6}$
$ x = 7\pi $
$x = \frac{7\pi}{\frac{1}{3,6}}$$\Leftrightarrow$$ x = {7\pi}\cdot {3,6}$
$$\color{Brown}{x = 25,2\pi\, km/h}$$
03. (UFPR) Um ponto em movimento circular uniforme descreve 15 voltas por segundo em uma circunferência de $R= 8,0\, cm$ . A sua velocidade angular, o seu período, a sua velocidade linear e aceleração centrípeta, são, respectivamente:
A velocidade angular é:
$f = 15,0\, Hz$
$w = 2\pi\cdot f$$\Leftrightarrow$$ w = 2\pi\cdot 15$
$$\color{Brown}{w = 30\pi\, rad/s$$
O período é o inverso da frequência.
$T = \frac{1}{f}$$\Leftrightarrow$$T = \frac{1}{15}\simeq 0,067\, s$
$$\color{Brown}{T \simeq 0,067\, s$$
A velocidade linear é dada por:
$$V = 2\pi\cdot R\cdot f$$
$V = 2\pi\cdot {8.0}\cdot {15,0} = 240\pi\, cm/s$
$$\color{Brown}{V = 240\pi\, cm/s}$$
Aceleração centrípeta:
$$a_{cp}= \frac{v^{2}}{R}$$
$a_{cp}= \frac{{240\pi}^{2}}{8,0}$$\Leftrightarrow$$a_{cp}= 57600\pi^{2}{8,0}$
$\color{Brown}{a_{cp} = 7200\pi^{2}\, cm/s^{2}}$
04. O tacômetro é um equipamento que fica no painel do carro para indicar ao motorista em tempo real qual é a frequência de rotação do motor. Supondo que um tacômetro esteja indicando 3000 rpm, determine a velocidade angular de rotação do motor em rad/s.
$f = 3000 rpm$$\Leftrightarrow$$ f =\frac{3000}{60} = 50 Hz$
$$\color{Blue}{w = 2\pi\cdot f}$
$\color{Brown}{w = 2\pi\cdot 50 = 100\pi\, rad/s}$
Exercícios para resolver
01. Um eucalipto encontra-se plantado perpendicularmente a uma superfície plana. A árvore é cortada junto ao chão e leva $t = 4\,s$ para deixar a posição vertical e ficar no chão na posição horizontal. Determine o valor aproximado da velocidade angular média de queda desse eucalipto.
02. – (PUC-SP) Lucas foi presenteado com um ventilador que, $t = 20\, s$ após ser ligado, atinge uma frequência de 300\,rpm em um movimento uniformemente acelerado.
O espírito científico de Lucas o fez se perguntar qual seria o número de voltas efetuadas pelas pás do ventilador durante esse intervalo de tempo. Usando seus conhecimentos de Física, ele encontrou
03. (UFRS) Um corpo em movimento circular uniforme completa 20 voltas em 10 segundos. O período (em s) e a frequência (em Hz) do movimento são, respectivamente.
04. – (Unifesp) Pai e filho passeiam de bicicleta e andam lado a lado com a mesma velocidade. Sabe-se que o diâmetro das rodas da bicicleta do pai é o dobro do diâmetro das rodas da bicicleta do filho.
Pode-se afirmar que as rodas da bicicleta do pai giram com:
( )a) a metade da frequência e da velocidade angular com que giram as rodas da bicicleta do filho;
( )b) a mesma frequência e velocidade angular com que giram as rodas da bicicleta do filho;
( )c) o dobro da frequência e da velocidade angular com que giram as rodas da bicicleta do filho;
( )d) a mesma frequência das rodas da bicicleta do filho, mas com metade da velocidade angular;
( )e) a mesma frequência das rodas da bicicleta do filho, mas com o dobro da velocidade angular.
05. O Brasil pode se transformar no primeiro país das Américas a entrar no seleto grupo das nações que dispõem de trens-bala. O Ministério dos Transportes prevê o lançamento do edital de licitação internacional para a construção da ferrovia de alta velocidade Rio-São Paulo. A viagem ligará os 403 quilômetros entre a Central do Brasil, no Rio, e a Estação da Luz, no centro da capital paulista, em uma hora e 25 minutos. Disponível em: http://oglobo.globo.com. Acesso em: 14 jul. 2009.
Devido à alta velocidade, um dos problemas a ser enfrentado na escolha do trajeto que será percorrido pelo trem é o dimensionamento das curvas. Considerando-se que uma aceleração lateral confortável para os passageiros e segura para o trem seja de 0,1 g, em que g é a aceleração da gravidade (considerada igual a 10 m/s² ), e que a velocidade do trem se mantenha constante em todo o percurso, seria correto prever que as curvas existentes no trajeto deveriam ter raio de curvatura mínimo de que valor aproximado?
06. (Fuvest) – Uma estação espacial foi projetada com formato cilíndrico, de raio R igual a 100 m, como ilustra a figura abaixo. Para simular o efeito gravitacional e permitir que as pessoas caminhem na parte interna da casca cilíndrica, a estação gira em torno de seu eixo, com velocidade angular constante $ω$. As pessoas terão sensação de peso, como se estivessem na Terra, se a velocidade ω for de, aproximadamente quanto?
07. Um disco pode girar em torno de um eixo que passa pelo centro. Partindo do repouso, com aceleração angular de $\gamma = \frac{\pi}{30}\, rad/s^{2}$ ele aumenta sua rotação por um intervalo de $\Delta t = {80,0}\, s$. Determine: a) a sua velocidade angular após esse intervalo de tempo; b) a frequência do disco depois de estabilizar o movimento; c) a velocidade tangencial nesse instante; d) o período de rotação do disco; e) a aceleração centrípeta que age sobre uma partícula localizada na borda do disco.
08. Uma partícula em movimento circular uniforme completa 2 voltas em uma circunferência de raio igual a $R=2,0\,m$, em um intervalo de tempo de $t=4,0\,s$. Determine o período e a frequência desse movimento.
( )a) 0,5 Hz e 2,0 s;
( )b) 0,4 Hz e 4,0 s;
( )c) 4,0 Hz e 2,0 s;
( )d) 2,0 Hz e 4,0 s;
( )e) 2,4 Hz e 5,0 s.
09. (MACK-SP) – Devido ao movimento de rotação da Terra, uma pessoa sentada sobre a linha do Equador tem velocidade escalar, em relação ao centro da Terra, igual a:
Adote: Raio equatorial da Terra $R= 6 300\,km$ e $\pi = \frac{22}{7}$
( )a) 2250 km/h;
( )b) 1650 km/h;
( )c) 1300 km/h;
( )d) 980 km/h;
( )e) 460 km/h.
11. (UFPR) – Um ponto em movimento circular uniforme descreve 15 voltas por segundo em uma circunferência de 8,0 cm de raio. A sua velocidade angular, o seu período e a sua velocidade linear são, respectivamente:
( )a) 20 rad/s; (1/15) s; 280 π cm/s;
( )b) 30 rad/s; (1/10) s; 160 π cm/s;
( )c) 30 π rad/s; (1/15) s; 240 π cm/s;
( )d) 60 π rad/s; 15 s; 240 π cm/s;
( )e) 40 π rad/s; 15 s; 200 π cm/s.
12. Uma serra circular possui 30 cm de diâmetro e opera com frequência máxima de $f=1200\,rpm$. Determine a velocidade linear de um ponto na extremidade da serra.
DADOS: $\pi = 3$
( )a) 12\,m/s;
( )b) 14\,m/s;
( )c) 16\,m/s;
( )d) 18\,m/s;
( )e) 20\,m/s.
13. (UFRGS) – Um corpo em movimento circular uniforme completa 20 voltas em 10 segundos. O período em $s$ e a frequência em $s^{-1}$ do movimento são, respectivamente:
( )a) 0,50 e 2,0;
( )b) 2,0 e 0,50;
( )c) 0,50 e 5,0;
( )d) 10 e 20;
( )e) 20 e 2,0.
14. (Unifor) – Um carrossel gira uniformemente, efetuando uma rotação completa a cada $T=4,0\,s$. Cada cavalo executa movimento circular uniforme com frequência em $f=rps$ (rotação por segundo) igual a:
( )a) 8,0;
( )b) 4,0;
( )c) 2,0;
( )d) 0,5;
( )e) 0,25.
15. Um corpo em MCU consegue realizar $n =480 voltas$ no tempo de $t = 120\,s$ em torno de uma circunferência de raio $R = 0,5\,m$. De acordo com essas informações, determine:
a) frequência e período.
b) velocidade angular e velocidade escalar.
16. (UFPE) – As rodas de uma bicicleta possuem raio igual a $R = 0,5\,m$ e giram com velocidade angular igual a $\omega = 5,0\,rad/s$. Qual a distancia percorrida, em metros, por essa bicicleta num intervalo de tempo de $t=10\,s$.
17. (UMC) – Numa pista circular horizontal,de raio igual a $R = 2\,km$, um automóvel se movimenta com velocidade escalar constante, cujo módulo é igual a $v =72\,km/h$. Determine o módulo da aceleração centrípeta do automóvel, em $m/s^{2}$.
18, (UEM) – Sobre o movimento circular uniforme, assinale o que for correto.
01. Período é o intervalo de tempo que um móvel gasta para efetuar uma volta completa.
02. A frequência de rotação é dada pelo número de voltas que um móvel efetua por unidade de tempo.
04. A distância que um móvel em movimento circular uniforme percorre ao efetuar uma volta completa é diretamente proporcional ao raio de sua trajetória.
08. Quando um móvel efetua um movimento circular uniforme, sobre ele atua uma força centrípeta, a qual é responsável pela mudança na direção da velocidade do móvel.
16. O módulo da aceleração centrípeta é diretamente proporcional ao raio de sua trajetória.
A soma das afirmações corretas é quanto?
19. (UERJ) – A distância média entre o Sol e a Terra é de cerca de 150 milhões de quilômetros. Assim, a velocidade média de translação da Terra em relação ao Sol é, aproximadamente, de:
( )a) 3\,km/s;
( )b) 30\,km/s;
( )c) 300\,km/s;
( )d) 3000\,km/s;
( )e) 30000\,km/s.
20. (UEMG) – Em uma viagem a Júpiter, deseja-se construir uma nave espacial com uma seção rotacional para simular, por efeitos centrífugos, a gravidade. A seção terá um raio de $R=90\,m$. Quantas rotações por minuto (RPM) deverá ter essa seção para simular a gravidade terrestre? (considere $g = 10\,m/s^{2}$).
( )a) $\frac{10}{\pi}$;
( )b) $\frac{2}{\pi}$;
( )c) $\frac{20}{\pi}$;
( )d) $\frac{15}{\pi}$;
( )e) $\frac{12}{\pi}$.
21. (FAAP) – Dois pontos A e B situam-se respectivamente a 10 cm e 20 cm do eixo de rotação da roda de um automóvel em movimento uniforme. É possível afirmar que:
( )a) O período do movimento de A é menor quer o de B;
( )b) A frequência do movimento de A é maior que o de B;
( )c) A velocidade angular do movimento de B é maior que a de A;
( )d) As velocidades angulares de A e B são iguais;
( )e) As velocidades lineares de A e B têm mesma intensidade.
22. (UFBA) – Uma roda de raio $R_{1}$, apresenta velocidade linear $V_{1}$ nos pontos situados na superfície e velocidade linear $V_{2}$, nos pontos que distam $d = 5\,cm$ da superfície. Sendo $V_{1}$ 2,5 vezes maior de que $V_{2}$, qual o valor de $R_{1}$?
( )a) 6,3 cm;
( )b) 7,5 cm;
( )c) 8,3 cm;
( )d) 12,5 cm;
( )e) 13,3 cm.
Havendo dúvidas, não hesite. Entre em contato para esclarecer suas dificuldades.
Curitiba, 29 de abril de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
