Física – Mecânica, Movimentos Compostos.
Lançamentos oblíquos
No capítulo precedente estudamos os lançamentos horizontais. Agora iremos analisar os lançamentos oblíquos. Trata-se também de movimentos compostos, que descrevem uma parábola, porém, a direção da velocidade de lançamento é inclinada em relação à horizontal. O ângulo pode ser acima da horizontal e abaixo. A situação mais comum é acima da horizontal.
Lançamento oblíquo acima da horizontal
Vamos imaginar um lançador de morteiros. É um tubo, disposto em uma armação, capaz de disparar projéteis explosivos. Sua utilização foi intensa nas guerras do século XX, para atingir objetivos inimigos, situados por trás de elevações ou obstáculos, onde o tiro direto seria inviável. Usando de várias técnicas determina-se a inclinação do tubo de lançamento e a carga propulsora, tendo em vista a altura a ser transposta e a distância do alvo.
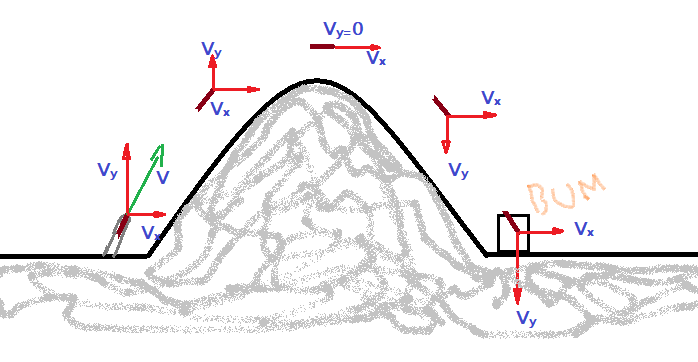
Na figura temos uma ilustração de como ocorre o lançamento de um obus de morteiro. Um projétil especial é introduzido em um tupo apropriado, colocado em uma inclinação conveniente. Na base do projétil são colocadas cargas propulsoras que disparam o projétil, numa velocidade inicial. Essa velocidade pode ser decomposta em duas componentes $V_{0X}$ e $V_{0Y}$. Inicialmente o projétil sobe enquanto se desloca na direção da elevação. Ao alcançar sua altura máxima, acima do topo, sua velocidade vertical se anula e inicia a queda. Enquanto isso a componente horizontal da velocidade permanece aproximadamente constante. Dessa forma a trajetória descrita é uma parábola, de concavidade para baixo. Se os cálculos da inclinação e da quantidade de propelente estiverem corretos, o projétil irá atingir o alvo situado do outro lado.
Aplicaremos as equações que usamos nos movimentos retilíneos, tanto o uniforme como o uniformemente variado. Começamos por decompor a velocidade de lançamento em suas componentes ortogonais $V_{0X}$ e $V_{0Y}$.
O ângulo de lançamento é medido em relação à linha horizontal e o representaremos por $\alpha$.
$\color{Blue}{V_{0X} = V_{0}\cdot cos\alpha}$
$\color{Blue}{V_{0Y} = V_{0}\cdot sen\alpha}$
O movimento horizontal é considerado uniforme e o vertical é uniformemente variado. Por isso as equações horárias de posição são:
$\color{Green}{X = V_{0X}\cdot t}$$\Leftrightarrow$$\color{Blue}{X = V_{0}\cdot\cos\alpha\cdot t}$
$\color{Green}{Y = V_{0Y}\cdot t – \frac{1}{2}\cdot g\cdot t^{2}}$$\Leftrightarrow$$\color{Blue}{Y =V_{0}sen\alpha\cdot t – \frac{1}{2}\cdot g\cdot t^{2}}$
Equação da trajetória do movimento
$X = V_{0}\cdot\cos\alpha\cdot t$$\Leftrightarrow$$ \color{Green}{t = \frac{X}{V_{0}\cdot\cos\alpha}}$
$Y = V_{0}\cdot sen\alpha\cdot \frac{X}{V_{0}\cos\alpha} – \frac{1}{2}\cdot g\cdot\frac{X^{2}}{V_{0}^{2}\cos^{2}\alpha}$
$\color{Blue}{Y = X\cdot tg\alpha – \frac{1}{2}\cdot g\cdot\frac{X^{2}}{{V_{0}}^{2}\cdot cos^{2}\alpha}}$
Altura máxima atingida
Com facilidade podemos deduzir que a altura máxima desse tipo de movimento é atingida no instante em que a componente vertical da velocidade se torna nula, invertendo o sentido daí em diante.
$v_{y}= v_{oy} – g\times t$$\Leftrightarrow$$ 0 = v_{oy} – g\times t_{m}$
$t_{m}=\frac{v_{oy}}{g}$$\Leftrightarrow$$t_{m} = \frac{v_{o}\times sen\alpha}{g}$
$$\color{Navy}{t_{m}=\frac{v_{o}\times sen\alpha}{g}}$$
Equação de Torricelli:
$v_{y}^{2} = v_{oy}^{2} – 2gy_{m}$$\Leftrightarrow$$ 0 = {(v_{o}^\times sen\alpha)}^{2} – 2 g y_{m}$
$$\color{Navy}{y_{m} =\frac{v_{0}^{2}\times sen^{2}\alpha}{2g}}$$
Para retornar à altura de lançamento, vale o que foi visto para os movimentos verticais. O tempo gasto para descer é o mesmo gasto na subida e portanto;
$$\color{Navy}{t_{t} = \frac{2\times v_{o}\times sen\alpha}{g}}$$
Alcance horizontal
O móvel lançado obliquamente acima da horizontal irá tocar o solo, no mesmo nível do lançamento, no instante de tempo visto acima. Basta multiplicar a componente horizontal da velocidade pelo tempo gasto para subir e descer.
$$\color{Navy}{x_{m}=v_{o}\times cos\alpha\times t_{t}}$$
Substituindo $t_{t}$, teremos:
$$\color{Navy}{x_{m}=2\times v_{o}^{2}\frac{cos\alpha\times sen\alpha}{g}} = \frac{v_{o}^{2}\times sen(2\alpha)}{g}$$
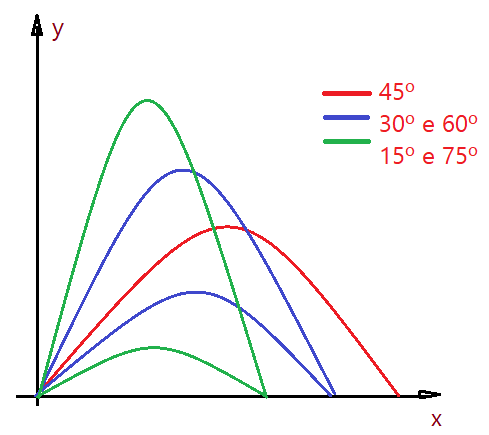
O alcance horizontal, como mostra a equação, depende de dois fatores principalmente. A componente da velocidade nesta direção e o tempo que o objeto fica em movimento, antes de atingir o solo. Elas variam com o ângulo de lançamento e podemos perceber que a condição em que o alcance será máximo é para um ângulo de $45^{o}$. Vejamos a figura abaixo, comparando as trajetórias para vários ângulos.
Estamos obviamente desprezando a resistência do ar, ventos e quaisquer empecilhos. Pode-se observar que ao aproximar o lançamento da posição vertical o alcance torna-se cada vez menor, terminando por chegar a zero, quando teremos um lançamento vertical.
Lançamento Oblíquo abaixo da horizontal.
Podemos fazer lançamentos abaixo da horizontal. Esse tipo de movimento é praticamente igual ao lançamento horizontal, com a diferença de que terá uma componente inicial da velocidade na vertical, o que não acontece no outro caso.
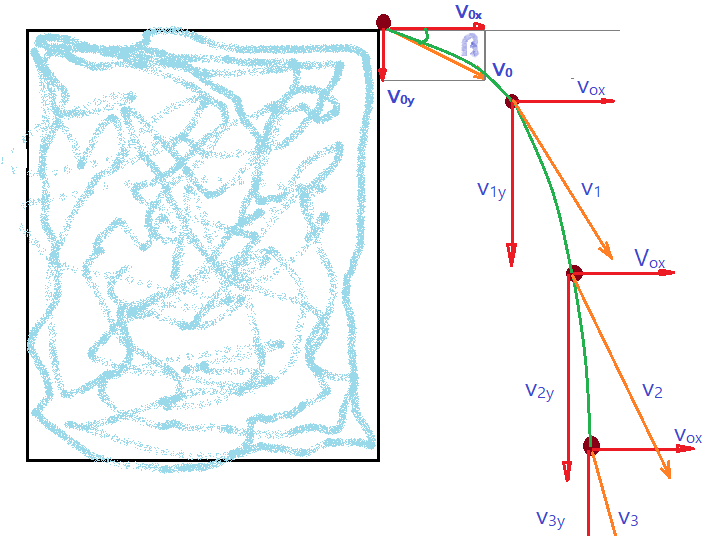
O movimento é parabólico como se fosse um lançamento horizontal, apenas na velocidade vertical teremos uma componente inicial, além da aceleração da gravidade.
$\color{Brown}{V_{0X} = V_{0}\cdot cos\beta}$$\Leftrightarrow$ essa componente é constante.
$V_{0Y} = V_{0}\cdot sen\beta$
$\color{Brown}{V_{Y} = – V_{0Y} – g\cdot t}$
As posições são dadas pelas equações horárias de MRU e MRUV.
$\color{Brown}{X = V_{0}\cdot cos\beta\cdot t}$
$\color{Brown}{Y = Y_{0} – V_{0}\cdot sen\beta\cdot t – \frac{1}{2}\cdot g\cdot t^{2}}$
Equação da trajetória no movimento
$X = V_{0}\cdot cos\beta\cdot t$$\Leftrightarrow$$ t = \frac{X}{V_{0}\cdot cos\beta}$
$Y = Y_{0} – V_{0}\cdot sen\beta\cdot \frac{X}{V_{0}\cdot cos\beta} – \frac{1}{2}\cdot g\cdot \frac{X ^{2}}{V_{0}^{2}\cdot cos^{2}\beta}$
$\color{Blue}{Y = Y_{0} – X\cdot tg\beta – \frac{1}{2}\cdot g\cdot\frac{X^{2}}{V_{0}^{2}\cdot cos^{2}\beta}}$
Hora de aplicar o aprendido
01. Um dispositivo de mola, colocado numa direção de $45^{0}$ acima da horizontal, dispara projéteis com velocidade inicial de $V_{0} = 50,0\, m\cdot s^{-1}$. Adotando $g = 10,0\, m\cdots^{-2}$, pergunta-se: a) qual é a altura máxima que o projétil alcança? b) qual é o tempo que o projétil demora para atingir a altura máxima? c) qual é o tempo para retornar ao nível do lançamento? d) qual é o alcance do projétil? e) escreva a equação da trajetória do projétil.
Para começar, vamos calcular as componentes $V_{0X}$ e $V_{0Y}$ da velocidade.
$V_{0X} = V_{0}\cdot cos\alpha$$\Leftrightarrow$$V_{0X}= {50,0}\cdot cos(45^{0})$
$\color{Brown}{V_{0X} = {50,0}\cdot \frac{\sqrt{2}}{2} = {25,0}\sqrt{2}\, m\cdot s^{-1}}$
$V_{0Y} = V_{0}\cdot sen\alpha$$\Leftrightarrow$$V_{0Y}={50,0}\cdot sen(45^{0})$
$\color{Brown}{V_{0Y} = {50,0}\cdot\frac{\sqrt{2}}{2}= {25,0}\sqrt{2}\, m\cdot s^{-1}}$
a) Vimos que o projétil começa a descer a partir do instante em que a sua velocidade vertical se anula. Logo nesse instante ele atingiu a altura máxima.
Podemos usar a equação de Torricelli para determinar $Y_{max}$.
$V_{Y}^{2} = V_{0Y}^{2}- 2\cdot g\cdot Y_{max}$*
$0 = {{25,0}\cdot\sqrt{2}}^{2} – 2\cdot{10,0}\cdot Y_{max}$
$20,0\cdot Y_{max} = 625,0\cdot 2$$\Leftrightarrow$$Y_{max} =\frac{1250,0}{20,0}$
$\color{Blue}{Y_{max} = 62,5\, m}$
b) o tempo para alcançar a altura máxima, obtemos pela equação da velocidade vertical.
$V_{Y} = V_{0Y} – g\cdot t$$\Leftrightarrow$$ 0 = {25,0}\cdot\sqrt{2} – {10,0}\cdot t_{mx}$
$t_{mx} = \frac{25,0\cdot\sqrt{2}}{10}$$\Leftrightarrow$$t_{mx}= {2,5}\cdot\sqrt{2}$
$\color{Blue}{t_{mx} \simeq 3,54\, s}$
c)o tempo para retornar ao nível do lançamento, habitualmente denominamos de alcance. Seria o instante em que o projétil toca o solo, supondo o lançamento neste nível e o terreno próximo plano.
No estudo do movimento de queda livre e lançamento vertical vimos que o tempo de atingir a altura máxima é igual ao tempo de queda na volta. Portanto o tempo para o projétil atingir o solo, será também o dobro do que gastou para atingir a altura máxima. Logo:
$t_{t} = 2\cdot t_{mx}$$\Leftrightarrow$$ t_{t}=2\cdot {2,5}\cdot\sqrt{2}$
$t_{t}= 5,0\sqrt{2}\, s$$\Leftrightarrow$$\color{Blue}{t_{t}\simeq 7,07\, s}$
d) o alcance depende da componente horizontal da velocidade e do tempo para chegar ao ponto de impacto.
$X = V_{0X}\cdot t_{t}$$\Leftrightarrow$$X = {25,0}\cdot {5,0}\cdot\sqrt{2}$
$\color{Blue}{X = {125,0}\cdot\sqrt{2} = 176,78\, m}$
e) equação da trajetória.
$Y = X\cdot tg\alpha – \frac{1}{2}\cdot g\cdot\frac{X^{2}}{{V_{0}}^{2}\cdot cos^{2}\alpha}$
$Y = X\cdot tg(45^{0}) – \frac{1}{2}\cdot g\cdot\frac{X^{2}}{{V_{0}}^{2}\cdot cos^{2}(45^{0})}$
$Y = X\cdot 1 – \frac{1}{2}\cdot 10\cdot\frac{X^{2}}{{(50,0)}^{2}\cdot \frac{\sqrt{2}^{2}}{{2}^{2}}}$
$Y = X – 5\cdot\frac{x^{2}}{{2500,0}\cdot \frac{\not{2}}{\not{4}}}$
$Y = X – \frac{5\cdot X^{2}\cdot 2}{2500\cdot 1}$
$Y = X – \frac{10\cdot X^{2}}{2500}$$\Leftrightarrow$$ Y = X – \frac{X^{2}}{250}$
$\color{Blue}{Y = X – \frac{X^{2}}{250,0}}$
02. Um projétil é lançado obliquamente com velocidade de $V_{0} = 30 m/s$, formando um ângulo $\alpha = 30^{0}$ com a horizontal. Em relação ao movimento desse projétil, $g= 10,0\, m\cdot s^{-2}$, calcule: a) A altura máxima atingida por ele; b) O alcance do projétil; c) a equação da trajetória.
Calculemos as componentes ortogonais da velocidade inicial.
$V_{0X} = V_{0}\cdot cos\alpha$$\Leftrightarrow$$V_{0X}={30,0}cos(30^{0})$
$V_{0X} = {30,0}\cdot\frac{\sqrt{3}}{2}$$\Leftrightarrow$$V_{0X}= {15,0}\cdot\sqrt{3}$
$V_{0Y}=V_{0}\cdot sen\alpha$$\Leftrightarrow$$V_{0X}={30,0}\cdot sen(30^{0})$
$V_{0Y}={30,0}\cdot\frac{1}{2} = 15,0\, m\cdot s^{-1}$
a) a altura máxima pode ser determinado com a equação de Torricelli.
$V_{Y}^{2} = V_{0Y}^{2} – 2\cdot g\cdot Y_{mx}$$\Leftrightarrow$$0 = {15,0}^{2} – 2\cdot{10,0}\cdot Y_{mx}$
${20,0}\cdot Y_{mx} = 225,0$$\Leftrightarrow$$ Y_{mx}=\frac{225,0}{20,0}$
$\color{Blue}{Y_{mx} = 11,25\, m}$
b)O alcance é a distância horizontal que o corpo percorre, num tempo igual ao dobro do tempo gasto para atingir a altura máxima.
$V_{Y} = V_{0Y} – g\cdot t$$\Leftrightarrow$$ 0 = {15,0} – {10,0}\cdot t_{mx}$
$t_{mx} = \frac{15,0}{10}$$\Leftrightarrow$$t_{mx} = 1,5\, s$
$t_{mx}= 1,5\, s$$\Rightarrow$$ t_{A} = 2\cdot t_{mx}$
$X_{A} = {15,0}\sqrt{3}\cdot 2\cdot{1,5} = {45,0}\sqrt{3} = 77,94\, m$
$\color{Blue}{X_{A} = 77,94\, m}$
$Y = X\cdot tg\alpha – \frac{1}{2}\cdot g\cdot\frac{X^{2}}{{V_{0}}^{2}\cdot cos^{2}\alpha}$
$Y = X\cdot tg(30^{0}) – \frac{1}{2}\cdot 10\frac{X^{2}}{{(30)}^{2}\cdot \frac{\sqrt{3}^{2}}{{2}^{2}}}$
$Y = \frac{\sqrt{3}}{3}\cdot X -\frac{5\cdot X^{2}}{900\cdot \frac{3}{4}}$
$Y = \frac{\sqrt{3}}{3}\cdot X – \frac{5\cdot 4\cdot X^{2}}{2700}$
$\color{Blue}{Y = \frac{\sqrt{3}}{3}\cdot X – \frac{X^{2}}{135}}$
03. Um avião caça voa à velocidade horizontal de $V_{X} = 900,0 km\cdot h^{-1}$, quando dispara um projétil bomba com velocidade de $V_{XR} = 60,0\, m\cdot s^{-1}$, num ângulo de $\alpha = 30^{0}$ abaixo da horizontal. Sendo $g= 10,0 m\cdot s^{-2}$, determine: a) a velocidade horizontal da bomba; b) a componente inicial da velocidade vertical da bomba; c) sendo a altura do lançamento igual a $Y_{0}= 1200,0\, m$, qual é o tempo até a bomba tocar o chão; d) qual é a distância do ponto de lançamento, medida na horizontal, até o ponto de impacto; e) a velocidade com que a bomba atinge o solo.
a) Para começar vamos calcular o valor da velocidade do caça na unidade do SI e as componentes da velocidade de lançamento do projétil.
Sabemos que $1 km\cdot ^{-1} = \frac{1}{3,6}\, m\cdot s^{-1}$
${900,0}\, km\cdot h^{-1} = x$
$ 1 km\cdot h^{-1} = \frac{1}{3,6}$
$x = {900,0}\cdot\frac{1}{3,6} = 250,0 m\cdot s^{-1}$
A velocidade da bomba logo após o lançamento será:
$V_{X} = V_{0X} + v_{x} = 250,0 + \frac{60\sqrt{3}}{2}$
$\color{Green}{V_{X} = 302\,m\cdot s^{-1}}$
b)componente vertical da velocidade
$V_{0Y} = V_{0}\cdot sen(30^{0})$$\Leftrightarrow$$\color{Brown}{V_{0Y}={60,0}\cdot \frac{1}{2} = 30,0\, m\cdot^{-1}}$
c)$Y = Y_{0} – V_{0Y}\cdot t – \frac{1}{2}\cdot g\cdot t^{2}$
$0 = 1200,0 – 30,0\cdot t – \frac{1}{2}\cdot {10,0}\cdot t^{2}$
$5\cdot t^{2} +30,0\cdot t – 1200,0 = 0$
Usando Baskahra:
$t =\frac{ -{30,0}\pm\sqrt{{30,0}^{2} – 4\cdot 5\cdot{(-1200,0)}}}{2\cdot {5,0}}$
$t = \frac{-{30,0}\pm\sqrt{900,0 + 24000}}{10}$
$t = \frac{-{30,0}\pm\sqrt{24900}}{2400}$$\Leftrightarrow$$t=\frac{-{30,0}\pm\ 157,8}{10}$
$t = \frac{-30,0+ 157,8}{10} = 12,78 s$
$t = \frac{-30,0 – 157,80}{10} = -18,78 s$ Este valor não existe, pois é negativo.
d)$X = V_{X}\cdot t$$\Leftrightarrow$$X = 302,0\cdot 12,78 $
$\color{Blue}{X = 3859,56\, m}$
e)$V_{Y}= V_{0Y} + g\cdot t$$\Leftrightarrow$$V_{Y}= 30,0 +{ 10,0}\cdot {12,78}$
$V_{Y}= 157,8 m\cdot s^{-1}$
$V^{2} = V_{X}^{2} + V_{Y}^{2}$$\Leftrightarrow$$V^{2}={302,0}^{2} + {157,8}^{2}$
$V^{2} = 91204 + 24900,84 = 116.104,84$$\Leftrightarrow$$\sqrt{V^{2}} = \sqrt{116.104,84}$
$\color{Blue}{V = 340,74\,m\cdot s^{-1}}$
É sua vez agora.
1. (CEFET-CE) – Duas pedras são lançadas do mesmo ponto no solo no mesmo sentido. A primeira tem velocidade inicial de módulo $V_{01} = 40 m/s$ e forma um ângulo $\alpha_{1} = 60^{0}$ com a horizontal, enquanto, para a outra pedra, este ângulo é $\alpha_{2} = 30^{0}$. Determine o módulo da velocidade da segunda pedra para que elas tenham o mesmo alcance. Considere a aceleração da gravidade igual a $g=10,0 m\cdot s^{-2}$
02. Um lança morteiros está instalado num ponto de altura $Y_{0} = 20,0 m$, em relação ao nível em que se encontra o alvo que pretende ser atingido. Sendo o lançamento feito em um ângulo $\alpha =30^{0}$, com velocidade de saída igual a $V_{0}= 180,0 m\cdot s^{-1}$ e tendo $g=10,0\, m\cdot s^{-2}$, qual é a distância entre as verticais que passam pelo ponto de lançamento e a localização do alvo?
03. Um canhão anti-aéreo lança granadas de $m = 15,0 kg$, com velocidade de saída na boca do cano $V_{0} = 720,0 m\cdot s^{-1}$. Deseja-se abater um avião cargueiro que está voando a altitude de $Y =6000,0 m e se aproxima com velocidade de $V_{c} = 648,0 km\cdot h^{-1}$. Com uma inclinação do cano em $\beta = 60^{0}$ com a horizontal, Qual deve ser o ângulo de visada do atirador ao avião, para que o tiro seja certeiro?
04. Um artilheiro militar, atira com um canhão, de cima de uma montanha, visando um tanque parado numa superfície plana, à $y = 1200,0 m abaixo do ponto de tiro. Sendo a distância horizontal entre o atirador e o alvo igual a $X = 2400,0 m$, o cano da arma está inclinado de $\beta = 30^{0}$ abaixo da horizontal. Em quanto tempo após o disparo o projétil atinge o alvo? Qual é a velocidade do projétil no instante do impacto? Escreva a equação da trajetória do projétil, tomando o nível em que se encontra o tanque como referencial. Adote $G = 10,0 m\cdot s^{-2}$.
05. Marque a alternativa incorreta a respeito do lançamento oblíquo.
a) O ângulo que fornecerá o maior alcance horizontal possível é o de $45^{o}$;
b) Ao chegar na altura máxima a componente vertical da velocidade do móvel é nula;
c) A componente horizontal da velocidade mantêm-se inalterada, uma vez que no eixo x o movimento é classificado como retilíneo e uniforme;
d) A componente vertical da velocidade diminui desde o solo até se tornar nula na altura máxima, o que classifica o movimento como sendo acelerado;
e) A componente horizontal da velocidade pode ser determinada pelo produto da velocidade do objeto com o cosseno do ângulo com o qual o corpo abandona o solo.
06. A bala de um canhão, com massa de %m=15\,kg$, é lançada com velocidade de $v = 1080\,km/h$. Determine o alcance horizontal máximo do projétil para o caso de o ângulo formado entre o canhão e a horizontal ser de $\gamma=15^{o}$.
Dados: $Sen 30^{o} = 0,5$
Gravidade $g= 10\,m/s^{2}$
a) 2,5 km;
b) 3,5 km;
c) 4,5 km;
d) 5,5 km;
e) 6,0 km.
07. (Uefs-BA) – Em um planeta X, uma pessoa descobre que pode pular uma distância horizontal máxima de $x_{max}= 20,0\,m$ se sua velocidade escalar inicial for de $V=4,0\,m/s$. Nessas condições, a aceleração de queda livre no planeta X, em $10^{-1}m/s^{2}$, é igual a:
a) 10,0;
b) 8,0;
c) 6,0;
d) 4,0;
e) 2,0.
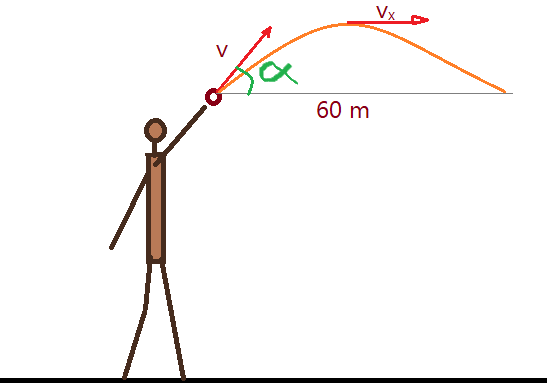
08. (Fatec-SP) – Em um jogo de futebol, o goleiro, para aproveitar um contra-ataque, arremessa a bola no sentido do campo adversário. Ela percorre, então, uma trajetória parabólica, conforme representado na figura, em 4 segundos.
Desprezando a resistência do ar e com base nas informações apresentadas, podemos concluir que os módulos da velocidade V, de lançamento, e da velocidade $_{x}$, na altura máxima, são, em metros por segundos, iguais a, respectivamente,
Dados: $sen\gamma = 0,8$; $cos\gamma = 0,6$.
a) 15 e 25;
b) 15 e 50;
c) 25 e 15;
d) 25 e 25;
e) 25 e 50.
09. Um canhão dispara uma bala com velocidade inicial igual a $v_{o}=500\,m/s$ (em módulo), a $\alpha=45^{o}$ com a horizontal. Desprezando o atrito e considerando $g = 10\,m/s^{2}$, determine o alcance máximo horizontal da bala.
10. Um projétil é lançado segundo um ângulo de $\alpha=30^{o}$ com a horizontal, com uma velocidade de $v_{o}=200\,m/s$. Supondo a aceleração da gravidade igual a $g=10\,m/s^{2}$ e desprezando a resistência do ar, o intervalo de tempo entre as passagens do projétil pelos pontos de altura $h=480\,m$ acima do ponto de lançamento, em segundos, é:
(DADOS: $sen 30^{o} = 0,50$ e $cos 30^{o} = 0,87$)
a) 2,0;
b) 4,0;
c) 6,0;
d) 8,0;
e) 12.
11. (CEFET-CE) – Duas pedras são lançadas do mesmo ponto no solo no mesmo sentido. A primeira tem velocidade inicial de módulo $V_{1}= 20\,m/s$ e forma um ângulo de $\alpha_{1}=60^{o}$ com a horizontal, enquanto, para a outra pedra, este ângulo é de $\alpha_{2}=30^{o}$.
O módulo da velocidade inicial da segunda pedra, de modo que ambas tenham o mesmo alcance, desprezando a resistência do ar, é:
a) $10\,m/s$;
b) $10\sqrt{3}\,m/s$;
c) $15\,m/s$;
d) $20\,m/s$;
e) $20\sqrt{3}\,m/s$.
12. (PUCCAMP-SP) – Observando a parábola do dardo arremessado por um atleta, um matemático resolveu obter uma expressão que lhe permitisse calcular a altura $y$, em metros, do dardo em relação ao solo, decorridos $t$ segundos do instante de seu lançamento ($t = 0$).
Se o dardo chegou à altura máxima de $h_{m}=20\,m$ e atingiu o solo $t=4,0\,s$ após o seu lançamento, então, desprezada a altura do atleta, considerando $g=10\,m/s^{2}$, a expressão que o matemático encontrou foi:
( )a) $y = – 5t^{2} + 20t$;
( )b) $y = – 5t^{2} + 10t$;
( )c) $y = – 5t^{2} + t$;
( )d) $y = -10t^{2} + 50$;
( )e) $y = -10t^{2} + 10$.
13. (UFSM-RS) – Um índio dispara uma flecha obliquamente. Sendo a resistência do ar desprezível, a flecha descreve uma parábola num referencial fixo ao solo. Considerando o movimento da flecha depois que ela abandona o arco, afirma-se:
I. A flecha tem aceleração mínima, em módulo, no ponto mais alto da trajetória;
II. A flecha tem aceleração sempre na mesma direção e no mesmo sentido;
III. A flecha atinge a velocidade máxima, em módulo, no ponto mais alto da trajetória.
Está (ão) correta(s):
a) apenas I;
b) apenas I e II;
c) apenas II;
d) apenas III;
e) I, II e III.
14. Um projétil é lançado obliquamente com velocidade de $v =30\, m/s$, formando um ângulo de $\alpha=30^{o}$ com a horizontal. Em relação ao movimento desse projétil, calcule:
Dados: $g= 10\,m/s^{2}$
a) A altura máxima atingida por ele.
b) O alcance máximo do projétil.
Se tiver dúvidas sobre qualquer questão resolvida ou proposta, faça contato comigo para que eu possa lhe ajudar.
Curitiba, 26 de abril de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760 Celular e WhatsApp: (41) 99805-0732
