Física – Mecânica
Associação de molas
Molas em paralelo
Vejamos a figura que ilustra a situação.
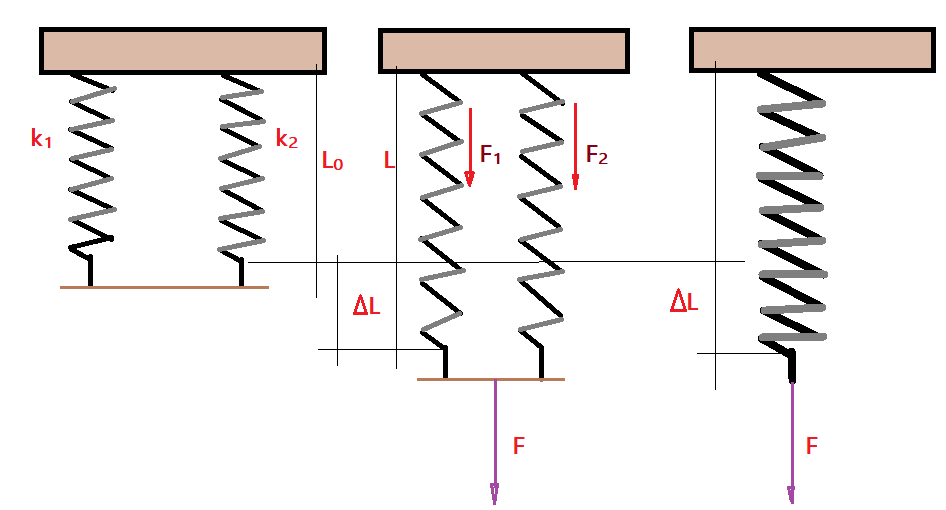
Ao associar duas molas em paralelo, temos que levar em conta dois aspectos. Para funcionar adequadamente, convém que elas tenham o mesmo comprimento e também sejam de constantes elásticas aproximadamente iguais. Se elas tiverem os valores das constantes muito diferentes, precisaremos ajustar a posição da aplicação da força de tração ou compressão.
Observamos que ambas sofrem deformações iguais $\Delta L_{1} = \Delta L_{2}$. Uma mola equivalente deverá ter a constante elástica com valor igual à soma das constantes das molas associadas.
$ k_{e} = k_{1} + k_{2}$
Cada mola suporta uma parte da força:
$F_{1} = k_{1}\cdot\Delta L $
$F_{2} = k_{2}\cdot\Delta L$
$F = F_{1} + F_{2}$$\Leftrightarrow$$ F = k_{1}\cdot\Delta L + k_{2}\cdot\Delta L$
$\color{Blue}{F = (k_{1} + k_{2})\cdot\Delta L}$
Para o caso de associarmos várias molas, representaremos o número delas por $n$.
$\color{Brown}{F = \sum_{1}^n k_{n}\cdot \Delta L}$
Molas em série
Vejamos a figura ilustrativa.
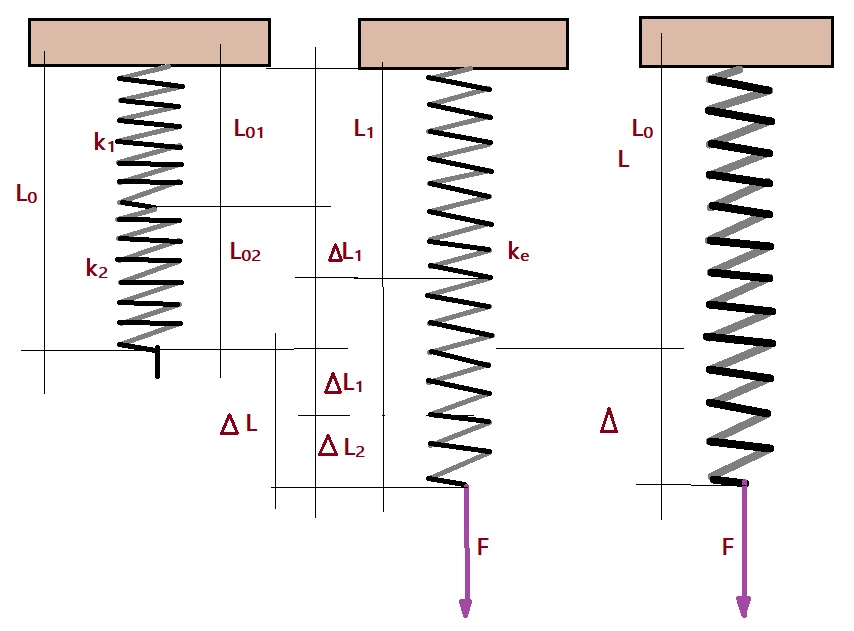
A força aplicada F, atua igualmente sobre ambas as molas. A deformação total será a soma das deformações individuais.
$F = k_{1}\cdot\Delta L_{1}$$\Leftrightarrow$$ \Delta L_{1} = \frac{F}{k_{1}}$
$F = k_{2}\cdot\Delta L_{2}$$\Leftrightarrow$$\Delta L_{2} = \frac{F}{k_{2}}$
$F = k_{e}\cdot\Delta L$$\Leftrightarrow$$\Delta L = \frac{F}{k_{e}}$
$\Delta L = \Delta L_{1} + \Delta L_{2}$
$\frac{\not{F}}{k_{e}} = \frac{\not{F}}{k_{1}} + \frac{\not{F}}{k_{2}} $
$\frac{1}{k_{e}} = \frac{1}{k_{1}} + \frac{1}{k_{2}}$
Para um número qualquer de molas associadas:
$\color{Brown}{\frac{1}{k_{e}} = \sum_{1}^n \frac{1}{k}}$
Há ainda um detalhe a analisar sobre elasticidade. Especialmente de molas, mas também se aplica às demais situações.
Na aparência, depois de cessada a tensão deformante, o corpo retorna à sua forma original. Isso é apenas aproximadamente verdadeiro. Quem já não ouviu a afirmação de que as “molas estão cansadas”, pode ser no veículo, num estofado e em todas as situações em que se usa as deformações elásticas com finalidades práticas. O que significa esse tal cansaço? É denominado deformação residual.
Deformação residual
A cada deformação sofrida, o corpo elástico retém uma minúscula deformação residual. Sua dimensão é insuficiente para ser percebida individualmente. Mas, tal como muitos milhões de pequenos grãos de areia formam uma praia ou mesmo um deserto, a sucessão prolongada de deformações acaba por acumular uma deformação residual acumulada, que resulta no que se decidiu denominar fadiga. Fazendo uma comparação com uma pessoa, poderíamos dizer que é um estado comparável à exaustão da pessoa. Existem processos de eliminação dessas tensões acumuladas, visando devolver ao corpo sua elasticidade original ou pelo menos aproximar-se disso.
Vamos exercitar esse assunto
01. Um par de molas possuem cada uma comprimento $L_{0} = 0,45 m$ e seus coeficientes de elasticidade são iguais a $k = {700,0}N/m$. Associadas em paralelo e submetidas a uma força $F= {490,0}N}, qual é a deformação resultante?
$R_{e} = R + R = 2R$$\Leftrightarrow$$ R_{e} = 2\cdot{700,0} = 1400,0 N/m$
$F = k_{e}\cdot \Delta L$$\Leftrightarrow$$\Delta L = \frac{F}{k_{e}}$
$\Delta L = \frac{490,0}{1400,0}$$\Leftrightarrow$$\Delta L = 0,35 m$
$\color{Brown}{\Delta L = 0,35}$
02. Se associarmos as duas molas do exercício 01, mas em série, qual será o novo coeficiente de elasticidade e a deformação produzida por uma força de $F={210,0} N$.
$\frac{1}{k_{e}} = \frac{1}{k_{1}} + \frac{1}{k_{2}}$
$\frac{1}{k_{e}} = \frac{2}{k}$$\Leftrightarrow$$ k_{e} = \frac{k}{2}$
$\Delta L = \frac{F}{\frac{k}{2}}$$\Leftrightarrow$$\Delta L = \frac{210,0}{\left(\frac{700,0}{2}\right)}$
$\Delta L = \frac{210,0}{350,0}$$\Leftrightarrow$$\Delta L = 0,60 m$
$\color{Brown}{\Delta L = 0,60 m}$
A deformação de cada mola será igual à metade desse valor.
03. Um sistema de molas associada é formado com três molas de $k = {600,0}kgf/m$. Se elas são comprimidas de um comprimento inicial $L_{0}=0,60 m$ para $L_{1}= 0,45 m$, qual é a intensidade da força aplicada?
$k_{e} = 3\cdot k = 3\cdot {600,0}kgf/m$
$F = k_{e}\cdot \Delta L = {600,0}\cdot{0,15} = 90,0 kgf$
$\color{Brown}{F = 90,0 kgf}$
04. Associando em série três molas de constantes elásticas $k_{1}= {250,0}N/m$, $k_{2}={300,0} N/m$ e $k_{3} ={200,0} N\m$. Seus comprimentos iniciais são $L_{01} = {20,0} cm$, $L_{02} ={30,0} cm$ e $L_{03} = {25,0} cm$. Determine a constante elástica da mola equivalente, as deformações individuais das molas e a deformação total, produzidas por uma força de tração de $F = 50,0 N$.
$\frac{1}{k_{e}} = \frac{1}{k_{1}} + \frac{1}{k_{2}} + \frac{1}{k_{3}}$
$\frac{1}{k_{e}} = \frac{1}{250,0} + \frac{1}{300,0} + \frac{1}{200,0}$
$\frac{1}{k_{e}} = \frac{12 + 10 + 15}{3000,0}$$\Leftrightarrow$$\frac{1}{k_{e}} = \frac{37}{3000,0}$
$\color{Brown}{k_{e} = \frac{3000,0}{37}\simeq 81,08 N }$
$F = k_{e}\cdot \Delta L$$\Leftrightarrow$$50,0 = {81,08}\cdot \Delta L$
$\color{Brown}{\Delta L = \frac{50,0}{81,8}\simeq 0,617}$
As deformações individuais são:
$F = k_{1}\cdot \Delta L_{1}$$\Leftrightarrow$$50 = {250,0}\cdot\Delta L_{1}$
$\ color{Brown}{\Delta L_{1} = \frac{50,0}{250,0} = 0,2 m}$
$F = k_{2}\cdot\Delta L_{2}$$\Leftrightarrow$$ {50,0} = {300,0}\cdot\Delta L_{2}$
$\color{Brown}{\Delta L_{2} = \frac{50,0}{300,0} = \frac{1}{6}\simeq 0,617 m}$
$F = k_{3}\cdot\Delta L_{3}$$\Leftrightarrow$${50,0} = {200,0}\cdot\Delta L_{3}$
$\color{Brown}{\Delta L_{3} = \frac{50,0}{200,0} = 0,25 m}$
Podemos somar as deformações individuais e verificar se os valores conferem.
$\Delta L = \delta L_{1} + \Delta L_{2} + \Delta L_{3}$
$\Delta L = 0,20 + 0,167 + 0,25 = 0,617$$\Rightarrow$ deu o mesmo resultado.
Exercícios para resolver.
01. (UFG) Para proteção e conforto, os tênis modernos são equipados com amortecedores constituídos de molas. Um determinado modelo, que possui três molas idênticas, sofre uma deformação de 4 mm ao ser calçado por uma pessoa de 84 kg. Considerando-se que essa pessoa permaneça parada, a constante elástica de uma das molas será, em kN/m, de quanto?
02. (UPE) Um corpo de massa m está suspenso por duas molas ideais, paralelas, com constantes elásticas $k$ e deformadas de $\Delta L$. Sabendo que o sistema se encontra em equilíbrio, assinale a alternativa que expressa $k$. Dado: Considere a aceleração da gravidade g.
a)$k = \frac{2\cdot m\cdot g}{d}$;
b)$k =\frac{m\cdot g}{d}$;
c) $k =\frac{m\cdot g}{2\cdot d}$;
d)$k = \frac{2\cdot d}{m\cdot g}$;
e)$k = {m\cdot }g$.
03. Uma pessoa com massa de 80Kg está sobre uma plataforma cuja base é formada por 4 molas idênticas. Calcule a constante elástica das molas, sabendo que as molas sofreram deformação de 2cm.
O primeiro passo para resolver esse exercício é calcular a força peso sobre a plataforma. Feito isso, vamos dividir essa força por quatro, que é a quantidade de molas, ou seja, são quatro molas que exercem força elástica em direção oposta a força peso. A soma das quatro forças elásticas é igual a força peso.
04. Determine a constante elástica equivalente de uma associação de 5 molas, dispostas nos quatro cantos de um quadrado e uma no centro. Sobre elas repousa uma lâmina fina e resistente que serve de plataforma para apoiar os pés de uma pessoa. As dimensões do quadrado são $l = 40 cm$. Uma pessoa de massa $m = 70,0 kg$ está parada sobre a plataforma, produzindo uma deformação $\Delta L = 2 cm$. O peso da pessoa está uniformemente distribuído. Uma vez determinada a constante elástica equivalente, analise o valor das constantes elásticas individuais.
05. Você possui uma mola, cuja constante elástica é $k = {1800,0} N/m$. Se você a cortar em quatro partes iguais e associá-las em paralelo, Qual será a constante elástica equivalente dessa associação? Qual será a força capaz de produzir uma deformação $\Delta L = 5,0 cm$ na associação dessas quatro molas resultantes?
06. Uma mola de comprimento $l_{0} = 0,60 cm, é cortada em três pedaços iguais, resultando em três molas de mesma constante elástica. Depois associamos dois pedaços em paralelo e em série com o terceiro. Exprima a constante elástica equivalente dessa associação, em função do valor da constante da mola original.
Se houver dúvidas, peça ajuda por um dos canais abaixo.
Curitiba, 31 de março de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
