Física – Termologia – Transmissão de calor.
Ficou dito nos posts anteriores que calor é a forma de energia em trânsito entre dois corpos, ou dois pontos de um corpo, que se encontrem à temperaturas diferentes, indo naturalmente do corpo mais quente para o menos quente. Agora chegou o momento de estudarmos de que forma essa energia se desloca entre um corpo e outro, de um ponto ao outro e mesmo através do vácuo.
Condução
É a forma de transmissão que ocorre de uma molécula para outra, transmitindo parte de sua energia de vibração mais elevada para a outra. Dessa forma ocorre o fenômeno da condução de calor. Isso exige o contato entre corpos de temperaturas diferentes para que o fenômeno ocorra. Entre os pontos distintos de um corpo, já existe a continuidade material e isso equivale a haver corpos em contato.
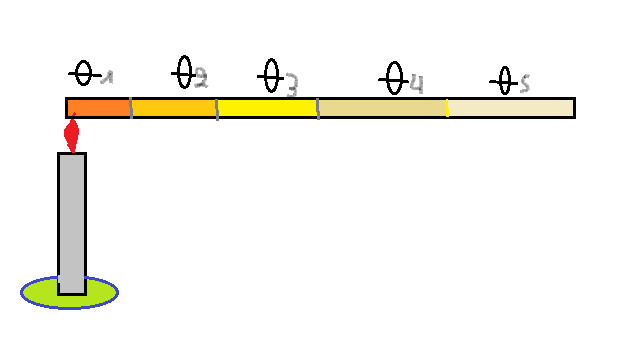

Segurando uma haste metálica, inicialmente em equilíbrio térmico, mantendo uma extremidade em contato com a chama de uma vela, irá ocorrer o aquecimento. As primeiras moléculas a serem aquecidas estão na extremidade em contato com a chama. Na medida que sua temperatura se eleva, elas com sua vibração transmitem energia às moléculas vizinhas e a temperatura vai se elevando ao longo da haste, até alcançar a outra extremidade. Poderá ocorrer um momento em que se torne inviável segurar a haste sem um instrumento de proteção da pele, devido a elevação da temperatura.
As temperaturas ao longo da haste manterão um gradiente de temperatura, isto é, quanto mais longe da chama estiver o ponto, menor será a temperatura atingida. Como as diferenças de temperatura entre dois pontos não vão ser constantes, ocorrendo uma gradual elevação da temperatura em cada ponto, o fluxo não será exatamente constante. Dizemos então que o regime é de condução em transiente, significando que o gradiente é transitório.
$\theta_{1} > \theta_{2} > \theta_{3} > \theta_{4} >\theta_{5}$
Fluxo de calor – Lei de Fourier
Denominamos fluxo de calor ao quociente entre a quantidade de energia térmica transmitida, pelo intervalo de tempo em que o fenômeno ocorreu.
Fluxo de calor é a quantidade de calor transmitida por condução na unidade de tempo.
$\color{Navy}{\Phi = \frac{Q}{\Delta t}}$ (I)
As unidades de fluxo de calor são tiradas dessa expressão:
No SI: $\Phi = {joule\over s}$ $\Rightarrow$$ \Phi = J/s = W$
No CGS: $\Phi = erg/s$
No MKgfS: $\Phi = kgm/s$
No sistema calorimétrico usual: $\Phi = cal/s$ ou $\Phi = kcal/s$
Do que depende o fluxo de calor?
A experiência demonstra que cada substância, em função de suas características físico-químicas, tem um modo mais ou menos intenso de transmitir calor por condução. A esse fator denominamos Condutibilidade térmica (também denominado condutividade) . Iremos representá-lo pela letra $k$.
Área da secção transversal que o calor irá percorrer. Não temos necessidade de pensar muito para intuir que quanto maior essa área for, maior será o fluxo de calor. Logo ele é diretamente proporcional à essa área $S$.
Diferença de temperatura é condição essencial para haver esse fluxo de calor e também se intui que o fluxo é tanto maior quanto maior for a diferença de temperaturas $\Delta\theta$. Diretamente proporcional.
Espessura da camada material, também podemos denominar distância entre os pontos com temperaturas diferentes. Vamos comparar um corredor indo de uma cidade à outra, com velocidade constante. Quanto maior for a distância, mais demora a chegar. Assim também é o fluxo de calor. Ele fica menor com o aumento da espessura, ou distância $\Delta X$ entre os pontos. É inversamente proporcional.
Essas considerações nos permitem entender a fórmula do fluxo de calor em função das grandezas que nele influenciam.
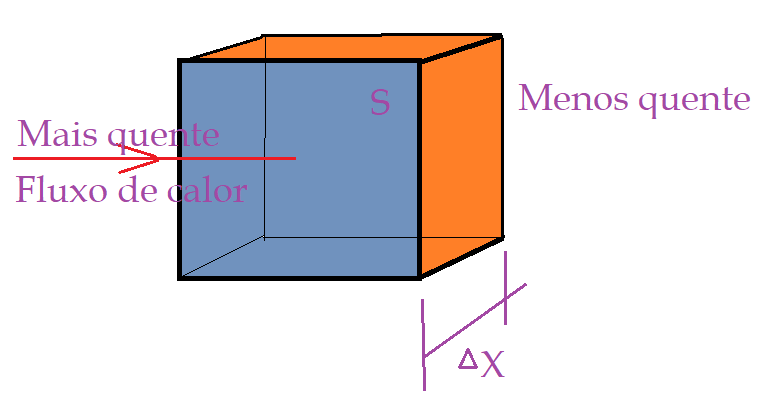
$$\color{Navy}{\Phi = k\times S\times\frac{\Delta\theta}{\Delta X}}$$ (II)
Combinando as equações (I) e (II), teremos:
${Q\over\Delta t} = k\cdot S\cdot{\Delta\theta\over\Delta X}$
$$\color{Navy}{Q = k\times S\times\frac{\Delta\theta\times\Delta t}{\Delta X}}$$
Evidenciando o coeficiente de condutividade térmica iremos ter:
$k = \frac{{Q\times\Delta{X}}{S\times\Delta\theta\times\Delta t}}$
Substituindo as variáveis do segundo membro pelas respectivas unidade
| Material | Condutibilidade térmica (a ) J/smK ou W/mK |
|---|---|
| Prata Grafeno | 426/429 4115 |
| Cobre | 398/401 |
| Alumínio | 237 |
| Tungstênio | 174/178 |
| Ferro | 80,2/80,3 |
| Vidro | 0,72 – 0,86 (0,79 médio) |
| Água | 0,61 |
| Tijolo | 0,4 – 0,8 |
| Madeira (pinho) | 0,11 – 0,14 |
| Fibra de vidro | 0,046/005 |
| Espuma de poliestireno | 0,03/0,033 |
| Ar | 0,026/0,03 |
| Espuma de poliuretano | 0,020 |
| Polipropileno | 0,25 |
| Epoxi | 0,30 |
| Epoxi (não cargueada) | 0,12 – 0,177 |
OBS.: A unidade de temperatura K, pode ser substituída pela correspondente ºC, sem alterar os valores. Para converter em calorias (cal) é apenas lembrar que $1cal = 4,186 J$. Uma pequena regra de três resolve a questão.
Condutores e isolantes térmicos
Os valores dos coeficientes de condutibilidade térmica nos permite classificar as substâncias em isolantes e condutores. As que têm elevado coeficiente de condutibilidade são condutores e aquelas em que esse fator é baixo, são isolantes.
Em verdade a linha divisória entre condutores e isolantes não fica nítida, mas evidentemente é fácil identificar um bom condutor e também um bom isolante, embora nenhum deles seja perfeito.
Exercícios
Exemplo 1. Uma sauna funciona na temperatura média em seu interior igual a $\theta_{1}= 50ºC$. A porta de acesso é feita de vidro, cuja espessura é $\Delta X = 12 mm$ e a área total da porta é de $S = 2,4 m²$. Sendo o coeficiente de condutibilidade térmica do vidro igual a $k = 0,8 J/msºC$ e a temperatura na parte externa igual a $\theta_{2} = 25ºC$, determine: a) o fluxo de calor constante através da porta; b) a quantidade de calor desperdiçada através da porta a cada hora de funcionamento.
$\Delta\theta = \theta_{1} – \theta_{2} = 50 – 25 = 25ºC$
$\Delta X = 12 mm = 1,2\cdot{10}^{-2} m$
$k = 0,8 J/msºC$
$S = 2,4 m²$
$\Phi = k\cdot S\cdot{{\Delta\Theta}\over\Delta X}$
$\Phi = 0,8\cdot {2,4}\cdot{{25}\over{1,2\cdot{10}^{-2}}}= 3983,3 J$
b) o calor desperdiçado por hora;
$Q = \Phi\cdot {3600} = {3983,3}\cdot {3600}= 14.339.880 J$
Se convertermos para a unidade caloria, teremos:
$\Phi = {{3983,3}\over{4,186}} = 951,58cal/s$
$Q = {{14.339.688}\over{4,186}} = 3.425.688 cal$
Exemplo 2. O aparelho de ar condicionado de uma sala está regulado para manter o ambiente na temperatura de $\theta_{2} = 18^0C$. Uma das paredes, sem janela, mede $l = 5,0\,m$ e $h = 3,0\,m$. Sendo a espessura de $\Delta X = 0,15\,m$ e o coeficiente de condutibilidade da alvenaria $k = 0,55\,J/sm^0C$. Nas horas mais quentes do dia, o lado externo atinge a tempertura de $\theta_{1} = 35^0C$. Quer-se saber qual é o fluxo de calor através dessa parede e qual a quantidade de calor que é introduzida por condução na sala durante uma hora.
Temos: $S = {5,0\times 3,0} = 15,0\,m^2$
$\Delta X = 0,15\,m$
$\Delta\theta = 35 – 18 = 17^0C$
$k = 0,55\,J/sm^0C$
$\Phi = k\cdot S\times\frac{\Delta\theta}{\Delta X}$
$\Phi = {(0,55)}\times {(15,0)}\times\frac{(17)}{(0,15)}$
$\Phi = 935\,J/s$$\Rightarrow$ este é o fluxo de calor.
$Q = {\Phi\cdot\Delta t}$$\Leftrightarrow$$Q={(935)}\cdot{(3600)} = 3366000J$
Se convertermos em calorias teremos:
$\Phi = {{(935)}\over{(4,186)}} = 223,36 cal$
$Q = {{(3366000)}\over{(4,186)}} = 804.108,93 cal$
Exercícios para resolver
1. (PUC-RS) No inverno, usamos roupas de lã baseados no fato de a lã:
a) ser uma fonte de calor.
b) ser um bom absorvente de calor.
c) ser um bom condutor de calor.
d) impedir que o calor do corpo se propague para o meio exterior.
e) n.d.a
2. (PUC-SP) Analise as afirmações referentes à condução térmica:
I – Para que um pedaço de carne cozinhe mais rapidamente, pode-se introduzir nele um espeto metálico. Isso se justifica pelo fato de o metal ser um bom condutor de calor.
II – Os agasalhos de lã dificultam a perda de energia (na forma de calor) do corpo humano para o ambiente, devido ao fato de o ar aprisionado entre suas fibras ser um bom isolante térmico.
III – Devido à condução térmica, uma barra de metal mantém-se a uma temperatura inferior à de uma barra de madeira colocada no mesmo ambiente.
Podemos afirmar que:
a) I, II e III estão corretas.
b) I, II e III estão erradas.
c) apenas I está correta.
d) apenas II está correta.
e) apenas I e II estão corretas.
3. (Mackenzie) Dos processos a seguir, o único onde praticamente todo o calor se propaga por condução é quando ele se transfere:
a) do Sol para a Terra.
b) da chama de um gás para a superfície livre de um líquido contido num bule que está sobre ela.
c) do fundo de um copo de água para um cubo de gelo que nela flutua.
d) de uma lâmpada acesa para o ar que a cerca.
e) de um soldador para o metal que está sendo soldado.
04. É comum o uso da expressão “o que é bom para o frio, também é bom para o calor”. À primeira vista isso parece paradoxal. Um exemplo disso pode ser observado nas roupas usadas pelos habitantes do deserto. Eles não usam roupas finas e justas ao corpo. Usam roupas, geralmente feitas de lã e em forma de túnicas que ficam folgadas e afastadas da pele. Isso se explica por:
a) a lã ser boa condutora de calor;
b)os tecidos finos são também bons condutores de calor;
c) a lã impede o calor de passar em qualquer sentido e sendo folgada fica distante da pele, mantendo uma camada de ar que é isolante;
d) essa afirmação não tem razão de ser;
e) os habitantes do deserto usam esse tipo de roupas por não terem outra espécie à disposição para usar.
05. Uma caixa de isopor contém $m = 10,0kg$ de gelo que se encontra inicialmente à temperatura de $\theta_{1} = -10ºC$. O ambiente externo está a $\theta_{2} = 30ºC$. Se a caixa mede $l = 0,50m$, $c = 0,70m$ e $h = 0,60m$, sendo o coeficiente de condutibilidade do material igual a $k = 0,015 J/smK$. O calor específico do gelo é $c = 0,5 cal/gºC$ e o calor latente de fusão é $L_{f}= 80 cal/g$. Em quanto tempo o gelo irá atingir a temperatura de fusão? Depois de atingir a temperatura de fusão, qual o intervalo de tempo decorrerá até o gelo virar água a 0ºC?(Despreze as perdas ocorridas pelas juntas de vedação e nos cantos).
06. Um tanque contém água à temperatura $\theta_{1}= 80ºC$ e uma das paredes que mede $1,2 x 1,0m$, tem espessura de $\Delta X = 10 mm$, está em contato com o ambiente externo onde a temperatura é $\theta_{2} =25ºC$. O tanque é feito de ferro, cujo coeficiente de condutividade térmica é $k = 80,2 J/smK$. Determine o fluxo de calor através dessa parede do tanque e a quantidade de calor perdida durante uma hora.
Havendo dúvidas, use de um dos canais abaixo e me consulte para esclarecer.
Curitiba, 20 de novembro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
