FI.ME.016.01 – Física – Mecânica, hidrostática. Princípio de Arquimedes, flutuação.
Empuxo – Princípio de Arquimedes.
Arquimedes viveu no século 3 a.C.. Entre as muitas heranças que nos legou, está o principio que leva seu nome O Princípio de Arquimedes.
- “Todo corpo imerso em um fluido, sofre a ação de uma força vertical, de baixo para cima, de intensidade igual ao peso do líquido deslocado.”
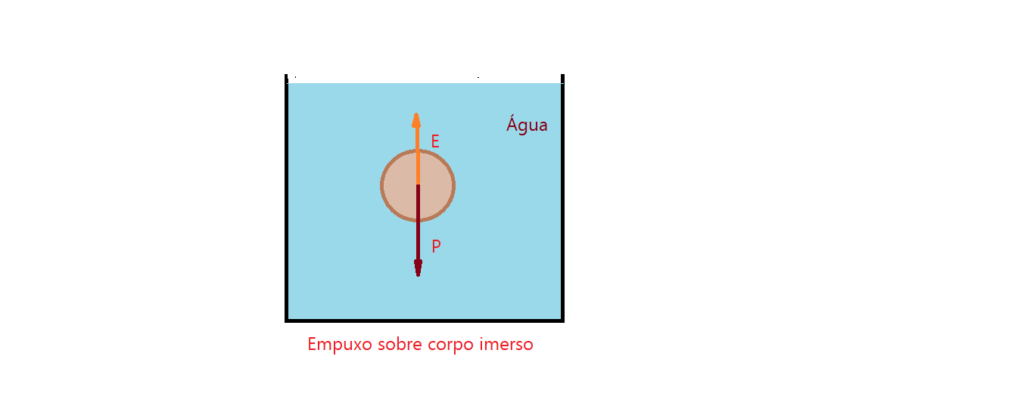
Se olharmos atentamente para a figura ao lado, vamos ver que a esfera colocada no interior do líquido, passou a ocupar um espaço que antes era ocupado por líquido. Isso provoca uma reação do líquido na forma de forças dirigidas em todas as direções contra as paredes do corpo imerso. O resultado é uma força denominada empuxo (E), dirigida verticalmente para cima, passando pelo centro de gravidade do corpo imerso. O valor do empuxo é igual ao peso do líquido de volume igual ao do corpo.
- $\bbox[5px,border:2px solid olive]{\color{navy}{{E} = P_{liq.des.}}}$
O peso do líquido deslocado é dado pelo produto da massa específica do líquido pelo volume do corpo, pela aceleração da gravidade.
- $\bbox[5px,border:2px solid olive]{\color{navy}{{E}={\mu_{liq}\cdot V_{corpo}\cdot {g}}}}$
Consequências do empuxo.
- Empuxo é menor que o peso do corpo.
Olhando para o corpo submerso, veremos que, se o peso é maior, haverá uma resultante das forças dirigida para baixo, de modo que o corpo irá descer até ao fundo do líquido. Esse movimento será uniformemente acelerado, mas com aceleração menor do que a gravidade.
- $\bbox[5px,border:2px solid Olive]{\color{Navy}{F_{R} = P – E}}$
- $\color{Navy}{{P – E} = {m\cdot {a}}}$
- $\color{Navy}{m\cdot g – \mu_{liq}\cdot V_{c}\cdot{g}= m\cdot{a}}$
- A massa do corpo pode ser calculada pelo produto da massa específica pelo volume.
- $\color{Navy}{\mu_c}\cdot {V_c}\cdot{g} – {\mu_{liq}\cdot{V_c}\cdot {g}}={\mu_c}\cdot{V_c}\cdot{a}$
O volume do corpo submerso é fator comum nos três termos da equação e por isso é cancelado.
- $\color{Navy}{{\mu_{c}\cdot{g}} – {\mu_{liq}\times{g}}= {\mu_c\times{a}}}$
- $\color{Navy}{{(\mu_{c} – \mu_{liq})}\times{g}= {\mu_{c}\times{a}}}$
- $\color{Navy}{ a={{(\mu_{c}-\mu_{liq})}\over{\mu_{c}}\times g}} $
- $\bbox[5px,border:2px solid Olive]{\color{Navy}{a=\left\{ 1 – {\mu_{liq}\over\mu_{c}}\right\}\times{g}}}$
- O empuxo é maior que o peso.
Facilmente percebemos que agora a resultante é dirigida para cima. Se o corpo estiver submerso a uma profundidade $\color{navy}{Y}$, irá subir até a superfície com movimento acelerado.
- $\bbox[5px,border:2px solid Olive]{\color{Navy}{a =\left\{1 – {\mu_{c}\over\mu_{liq}}\right\}\times{g}}}$
- O empuxo é igual ao peso.
Nesse caso o corpo ficará em equilíbrio em qualquer posição onde seja colocado, pois a resultante será igual a zero. Um exemplo dessa situação é um submarino navegando submerso. A igualdade entre peso e empuxo é conseguida colocando-se nos tanques de lastro a quantidade de água necessária. Temos:
- $\bbox[5px,border:2px solid Olive]{\color{Navy}{E = P}}$
- Corpos flutuantes.
Os corpos ocos ou feitos de materiais menos densos que os líquidos, ficam numa situação chamada de flutuação. Nessa condição o Peso e o Empuxo são iguais, pois o corpo fica apenas parcialmente imerso no líquido. Dessa forma o volume de líquido deslocado é menor que o volume do corpo. O estudo das condições de flutuação é fundamental para a construção de embarcações de qualquer espécie. Mesmo usando de materiais mais densos que a água, os cascos contém em seu interior um considerável volume de ar, situado abaixo da linha de flutuação, o que faz a densidade relativa ser menor, permitindo ao mesmo transportar cargas úteis, tanto de mercadorias quanto de passageiros.
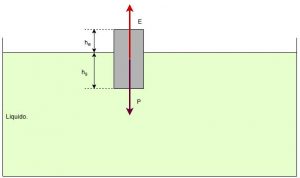
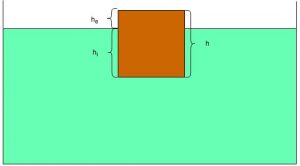
O corpo tem uma altura $\color{Navy}{h} $, da qual temos a parte $\color{Navy}{h_{e}}$, emersa e a parte $\color{Navy}{h_{i}}$, imersa no líquido. A razão entre as partes emersa e imersa depende da razão entre a massa específica (densidade) do corpo e da massa específica do líquido.
A navegação de qualquer tipo de barco tem que levar em consideração esse fato. Os icebergs, são imensos blocos de gelo, ligeiramente menos densos que a água do mar e por isso flutuam, tendo entre $90\mapsto 100\%$ de seu volume submerso, o que os torna tão perigosos para os navios em alto mar.
Os navios modernos têm seus cascos construídos em chapas metálicas, cuja densidade é consideravelmente maior que a da água, porém, conseguem flutuar porque seu volume interno é grandemente preenchido por ar, tornando a densidade relativa do casco, menor que a da água. Com isso, quando um navio está carregado, sua linha de flutuação fica acima do nível em que se localiza, quando está sem carga. Ao aumentar a parte submersa, aumenta o volume de água deslocada, mantendo o equilíbrio entre o empuxo e o peso total.
- Vamos resolver uns exercícios com o assunto visto até aqui.
- Uma esfera maciça de ferro é abandonada na superfície de um tanque cheio de água. Se a aceleração da gravidade no local é igual a 10 m/s², qual é a aceleração com que o corpo percorre a distância até o fundo? Temos que
- $\color{Navy}{\mu_{H_{2}O} = {10^3}\,kg/m^3}$
- $\color{Navy}{\mu_{F_e}= {7,9\times{10^3}}\,kg/m^3}$
Temos a fórmula determinada acima.
- $\bbox[5px,border:2px solid Olive]{\color{Navy}{a =\left\{1 – {\mu_{liq}\over\mu_{c}}\right\}\times{g}}}$
- $\color{Navy}{a =\left\{1- {{10^3}\over{7,9}\times{10^3}}\right\}\times{10}}$
- $\color{Navy}{a =\{1 – 0,1266\}\times{10}}$
- $\color{Navy}{a = {0,8734}\times{10}}$
- $\color{Navy}{a = 8,734 m/s^2}$
- A esfera irá afundar com aceleração de $8,734\,m/s^2$.
- Um bloco de material sintético, com massa específica $\color{Navy}{\mu_{s} = {0,8\times{10^3}}\,kg/m^3}$, é colocado no fundo de um tanque de água e solto. Qual é a aceleração ascendente com que o bloco sobe?
- $\color{Navy}{\mu_{H_{2}O} = {10^3}\,kg/m³}$
- $\color{Navy}{g = 10\,m/s^2}$
Agora usamos a fórmula com as massas específicas invertidas
- $\bbox[5px,border:2px solid Olive]{\color{Navy}{a = \left\{1 – {\mu_{S}\over\mu_{H_{2}O}}\right\}\times{g}}}$
- $\color{Navy}{a = \left\{1 -{{0,8}\times{10^3}\over{10^3}}\right\}\times{10}}$
- $\color{Navy}{a =\{1 – 0,8\}\times{10} = {0,2}\times {10}}$
- $\color{Navy}{a =2,0 m/s^2}$
O bloco irá subir em direção à superfície, com aceleração de $2,0\,m/s^2$.
- Um bloco de madeira, em forma de cubo, tem densidade igual a $\color{Navy}{\delta = 0,78}$. Ele flutua em água doce. Se sua aresta é de $\color{Navy}{a = 80\,cm}$, determinar a altura da parte emersa e imersa desse bloco. Sabe-se que $\color{Navy}{\mu_{H_{2}O}= {10^3} kg/m^3}$.
Como vimos para os corpos flutuantes, o peso do bloco é igual ao empuxo. Se a aresta o cubo é de $80\,cm$, o valor de $h $ é igualmente de $80\,cm$. A soma das a partes emersa e imersa é igual à altura h. A área da base é:
- $\bbox[5px,border:2px solid Olive]{\color{Navy}{A = h^{2}}}$
Vamos começar pela igualdade entre as forças de empuxo e peso.
- $\bbox[5px,border:2px solid Olive]{\color{Navy}{E = P}}$
- $\color{Navy}{m_{liq}\times{g}= m_{bl}\times{g}}$
A aceleração da gravidade é fator comum aos dois membros da equação e pode, por isso, ser cancelada, restando que a massa do líquido deslocada é igual à massa do bloco. O que diverge são os volumes e massas específicas.
Podemos então escrever:
- $\color{Navy}{m_{liq}= m_{bl}}$
- $\color{Navy}{\mu_{liq}\times V_{s} = \mu_{bl}\times V_{bl}}$
Tanto o volume total como o submerso são calculados pelo produto da área da base(quadrado), pela altura (aresta).
- $\color{Navy}{\mu_{liq}\times h_{i}\times h^2 = \mu_{bl}\times{h}\times h^2 }$
Cancelamos as áreas da base, ficando.
- $\color{Navy}{\mu_{liq}\times h_{i} = \mu_{bl}\times{h}}$
Substituindo os valores das variáveis.
- $\color{Navy}{{10^3}\times h_{i}= {0,78}\times{10^3}\times{0,80}}$
- $\color{Navy}{h_{i}={{{0,78}\times{10^3}\times{0,80}}\over{10^3}}}$
- $\color{Navy}{h_{i}= {0,78}\times{0,80}}$
- $\color{Navy}{h_{i}=0,624m}$
Determinamos a altura imersa. Vamos determinar a parte emersa.
- $\color{Navy}{h_{i} + h_{e} = h}$
- $\color{Navy}{h_{e}= h – h_{i}}$
- $\color{Navy}{h_{e}= {0,800 – 0,624}}$
- $\color{navy}{h_{e}=0,176 m}$
Temos agora que o bloco terá $0,624\,m$de sua aresta abaixo da linha d’água e $0,176\,m$ acima.
Exercitando o assunto
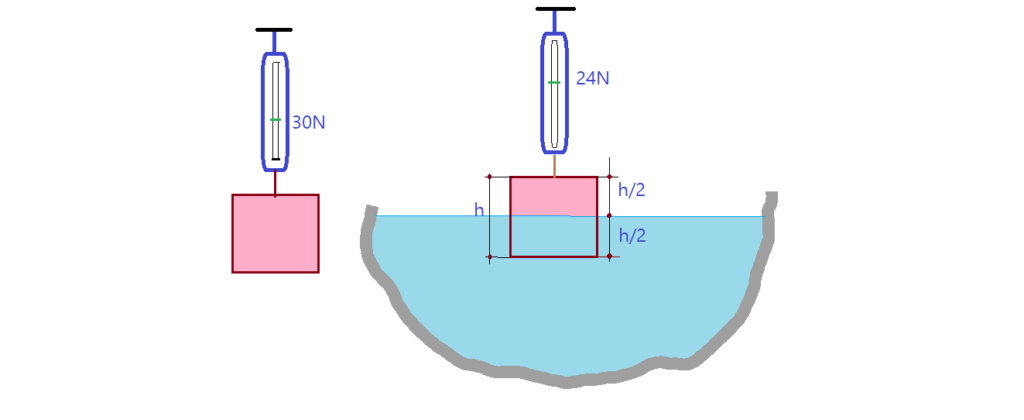
01. (Enem 2011) – Em um experimento realizado para determinar a densidade da água de um lago, foram utilizados alguns materiais conforme ilustrado: um dinamômetro D com graduação de 0 N a 50 N e um cubo maciço e homogêneo de $\color{Sepia}{10\,cm}$ de aresta e $\color{Sepia}{3\, kg}$ de massa. Inicialmente, foi conferida a calibração do dinamômetro, constatando-se a leitura de $\color{Sepia}{30\,N}$ quando o cubo era preso ao dinamômetro e suspenso no ar. Ao mergulhar o cubo na água do lago, até que metade do seu volume ficasse submersa, foi registrada a leitura de $\color{Sepia}{24\,N}$ no dinamômetro.
02. (Enem 2010) – Durante uma obra em um clube, um grupo de trabalhadores teve de remover uma escultura de ferro maciço colocada no fundo de uma piscina vazia. Cinco trabalhadores amarraram cordas à escultura e tentaram puxá-la para cima, sem sucesso. Se a piscina for preenchida com água, ficará mais fácil para os trabalhadores removerem a escultura, pois a:
( )a) escultura flutuará. Dessa forma, os homens não precisarão fazer força para remover a escultura do fundo;
( )b) escultura ficará com peso menor, Dessa forma, a intensidade da força necessária para elevar a escultura será menor;
( )c) água exercerá uma força na escultura proporcional a sua massa, e para cima. Esta força se somará á força que os trabalhadores fazem para anular a ação da força peso da escultura;
( )d) água exercerá uma força na escultura para baixo, e esta passará a receber uma força ascendente do piso da piscina. Esta força ajudará a anular a ação da força peso na escultura;
( )e) água exercerá uma força na escultura proporcional ao seu volume, e para cima. Esta força se somará à força que os trabalhadores fazem, podendo resultar em uma força ascendente maior que o peso da escultura.
03. (UERJ) – Uma barca para transportar automóveis entre as margens de um rio, quando vazia, tem volume igual a $\color{Sepia}{100 m^{3}}$ e massa igual a $\color{Sepia}{4,0\times 10^{4}\,kg}$. Considere que todos os automóveis transportados tenham a mesma massa de $\color{Sepia}{1,5\times 10^{3}\,kg}$ e que a massa específica da água seja de $\color{Sepia}{\mu = 1000,0\,kg/m^{3}}$. O número máximo de automóveis que podem ser simultaneamente transportados pela barca corresponde a:
( )a) 10;
( )b) 40;
( )c) 80;
( )d) 120;
( )e) 60.
04. (Mackenzie-SP) – Devido à crise hídrica que se instalou na cidade de São Paulo, um estudante, após a aula de hidrostática, resolveu colocar uma garrafa de 1,0 litro, cheia de água, no interior da caixa acoplada de descarga. Essa medida gerou uma economia de água no final de um período. Essa ideia colocada em prática foi baseada no:
( )a) Princípio de Stevin;
( )b) Princípio de Arquimedes;
( )c) Princípio de Pascal;
( )d) Princípio dos vasos comunicantes;
( )e) Teorema de Bernoulli.
05. Determine o empuxo sobre uma esfera de raio $\color{Sepia}{2\,cm}$ que tem $\color{Sepia}{\frac{1}{8}}$ de seu volume submerso em água.
Dados: $\pi = 3$; densidade da água $\mu = 1000\,kg/m^{3}$ e $g = 10\,m/s^{2}$
( )a) 0,05;
( )b) 0,03;
( )c) 0,08;
( )d) 0,04;
( )e) 0,02.
06. A respeito do Princípio de Arquimedes, o empuxo, marque a alternativa falsa.
( )a) O empuxo é uma força que sempre atua na vertical e para cima;
( )b) Se um objeto boia na superfície de um líquido, podemos dizer que o empuxo é maior que o peso, portanto, a densidade do líquido é maior que a densidade do objeto;
( )c) Se um objeto afunda ao ser colocado em um recipiente que contém determinado líquido, podemos dizer que o empuxo sobre o objeto é maior que o peso, portanto, a densidade do líquido é maior que a densidade do objeto;
( )d) A determinação do empuxo é feita pelo produto da densidade do líquido, volume imerso do corpo e aceleração da gravidade;
( )e) Todas as alternativas anteriores estão corretas.
07. Em um recipiente há um líquido de densidade absoluta $\color{Sepia}{\mu = 2,56\,g/cm^{3}}$. Dentro do líquido encontra-se um corpo de volume $\color{Sepia}{V_{c} = 1000\,cm^{3}}$, que está totalmente imerso. Qual o empuxo sofrido por este corpo? Dado $\color{Sepia}{g=10\,m/s^{2}}$
08. Um objeto de densidade absoluta $\color{Sepia}{\mu = 300\,kg/m^{3}}$ e massa $\color{Sepia}{m = 15.000\,kg}$ flutua nas calmas águas de um lago. Se a densidade absoluta do fluido é $\color{Sepia}{m_{Fl}= 1000\,g/m^{3}}$. determine o volume emerso do corpo.
09. (Mackenzie-SP) – Um navio flutua porque:
( )a) seu peso é pequeno quando comparado com seu volume;
( )b) seu volume é igual ao volume do líquido deslocado;
( )c) o peso do volume do líquido deslocado é igual ao peso do navio;
( )d) o peso do navio é menor que o peso do líquido deslocado;
( )e) o peso do navio é maior que o peso do líquido deslocado.
10. (Fuvest-SP) – Um objeto homogêneo colocado em um recipiente com água tem $\color{Sepia}{32\%}$ de seu volume submerso; já em um recipiente com óleo, esse objeto tem$\color{Sepia}{40\%}$ de seu volume submerso. A densidade desse óleo, em $\color{Sepia}{g/cm^{3}}$, é:
Note e adote: $\mu_{H_{2}O} = 1\,g/cm^{3}$
( )a) 0,32;
( )b) 0,40;
( )c) 0,64;
( )d) 0,80;
( )e) 1,25.
11. Marque a alternativa correta a respeito do empuxo.
( )a) O empuxo é uma força vertical e descendente, que atua sobre objetos mergulhados exclusivamente em líquidos;
( )b) O empuxo é uma força vertical e ascendente, que atua sobre objetos mergulhados em fluidos. Essa grandeza equivale ao peso de fluido deslocado pelo objeto mergulhado;
( )c) O empuxo terá o mesmo módulo da força peso;
( )d) O empuxo é uma força vertical e ascendente, que atua sobre objetos mergulhados exclusivamente em líquidos. Essa grandeza equivale ao peso de fluido deslocado pelo objeto mergulhado;
( )e) Todas as alternativas estão incorretas.
12. Um objeto, de volume $\color{Sepia}{0,5 m^{3}}$, possui $\color{Sepia}{30\%}$ do seu volume mergulhado em um recipiente com água. Sabendo que a densidade no local é de $\color{Sepia}{g = 9,8\,m/^{2}}$ e que a densidade da água é de $\color{Sepia}{\mu_{H_{2}O} =1000\,kg/m^{3}}$, determine o empuxo sobre o objeto.
( )a) 1000 N;
( )b) 4700 N;
( )c) 2700 N;
( )d) 1550 N;
( )e) 1470 N.
13. Um colchão de isopor de $\color{Sepia}{c = 2,0\,m}$ de comprimento, $\color{Sepia}{l = 40\,cm}$ de largura e $\color{Sepia}{h = 5,0\,cm}$ de altura flutua em posição horizontal sobre a água de uma piscina. Um banhista deita sobre o colchão permanecendo este em posição horizontal. Observa-se, então, que a água aflora justo na superfície superior do colchão. Sabendo que a massa específica da água vale $\color{Sepia}{\mu = 1,0\, g/cm^{3}}$, conclui-se que a massa do banhista vale:
( )a) 100 kg;
( )b) 80 kg;
( )c) 60 kg;
( )d) 40 kg;
( )e) 20 kg.
O que vimos aqui, vai ajudar a resolver uma boa quantidade de problemas práticos com que poderá se deparar na vida.
Em caso de dúvidas, faça contato por um dos canais listados abaixo.
Curitiba, 14 de maio de 2015 (Revisado e atualizado em 08/08/2016)
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732