FI.ME.010-01 – Física – Mecânica, estática. Resultante de forças ortogonais.
Resultante de forças ortogonais.
No estudo da adição de vetores, vimos que se eles são ortogonais (90^0), recorremos à aplicação do Teorema de Pitágoras. Portanto se queremos determinar a resultante de duas forças concorrentes ortogonais, fazemos a mesma coisa, pois são grandezas vetoriais e as representamos graficamente por vetores.
Vejamos a resultante de das forças $\color{Navy}{F_{1} = 6,0\,N}$ e $\color{Navy}{F_{2} = 8,0\,N}$ formando entre elas um ângulo reto ($\color{navy}{\theta = 90^0}$).
Aplicando a fórmula já nossa conhecida, teremos;
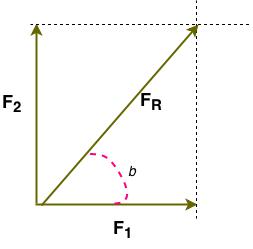
- $\color{Olive}{{F_{R}}^2 = {F_{1}}^2 + {F_{2}}^2}$
- $\color{Navy}{{F_{R}}^2 = {(6,0)}^2 + {(8,0)}^2}$
- $\color{Navy}{{F_{R}}^2 = 36,0 + 64,0}$
- $\color{Navy}{{F_{R}}^2 = 100,00}$
- $\color{Navy}{F_{R} = \sqrt[2] {100,0}}$
- $\color{Brown}{F_{R} = 10,0\,N}$
Falta determinar a direção da força resultante.
- $\color{Olive} {{tg b} = \frac {8,0}{6,0}}$
- $\color{Navy}{{tg b} = \frac {4}{3}}$
Podemos dizer que: - $\color{Brown}{ b = {arc tg \frac {4}{3}}}$
A força resultante forma com a força horizontal de 6,0 N um ângulo cuja tangente é igual a 4/3.
Vamos colocar um exemplo de uma situação prática. Um sulcador agrícola, tracionado por uma parelha de bois, recebe desta uma força horizontal de $1500\,N$. Na direção vertical agem sobre ele a força peso de $600,0\,N$, além de um peso adicional colocado sobre ele de $400\,N$. Vamos determinar a resultante dessas duas forças de direções ortogonais.
Veja uma representação esquemática do problema.
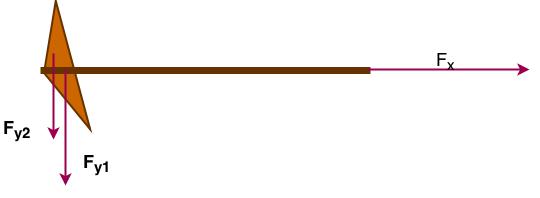
Temos o corpo sob a ação de três forças, sendo duas de mesma direção e sentido. Podemos representar o sistema num diagrama de forças, no par de eixos coordenados $\color{Navy}{\widehat{XOY}}$. Ficando assim:
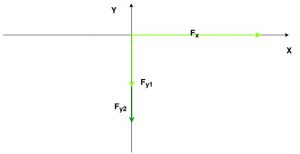
As forças peso do sulcador e do peso adicional tem a mesma direção e sentido (vertical para baixo). Aplicando a adição de forças de mesma direção e sentido, resulta uma única força vertical para baixo, com módulo igual à soma dos módulos das duas forças componentes.
- $\color{Olive} {F_{y_{1}} + F_{y_{2}} = F_{y}} $
- $\color{Navy}{F_{y} =( – 600,0) + (- 400,0)}$
- $\color{Navy}{F_{y} = – 1000,0 N}$
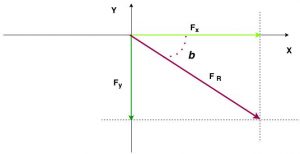
Agora vamos aplicar o Teorema de Pitágoras na determinação da força resultante do sistema.
- $\color{Olive}{{F_{R}}^2 ={F_{x}}^2 + {F_{y}}^2}$
- $\color{Navy}{{F_{R}}^2 = {(1500,0)}^2 + {(- 1000,0)}^2}$
- $\color{Navy}{{F_{R}}^2 = {2250000,0 + 1000000,0} = {2,25\cdot{10}^6} +{1,0\cdot{10}^6}}$
- $\color{Navy}{{F_{R}}^2 = {3,25\cdot{10}^6}}$
- $\color{Navy}{F_{R} = \sqrt[2]{3,25\cdot{10}^6}}$
- $\color{Brown}{F_{R} \simeq {1,8\cdot {10}^3}\,N}$
O ângulo $\color{Brown}{\hat{b}}$ que a resultante forma com a horizontal é abaixo dessa linha. Obedecendo à orientação dos eixos, iremos encontrar uma tangente negativa para esse ângulo. No círculo trigonométrico isso corresponde a um ângulo situado no quarto quadrante.
- $\color{Navy}{{tg b} = \frac{(-1000)}{(1500)} = \frac{-10}{15} = \frac{-2}{3} = -(2/3)}$
Teremos portanto um ângulo $\color{Brown}{b = arc tg (-{2\over 3})}$. Em valores aproximados corresponde a um ângulo de aproximadamente $37^0$ abaixo da horizontal, dirigido para direita, levando em conta que efetuamos o raciocínio considerando a força horizontal orientada da esquerda para direita.
Hora de fazer alguns exercícios.
Determinar a força resultante de sistemas com duas forças ortogonais.
- $\color{Navy}{F_{1} = 12,0\,N}$ e $\color{Navy}{F_{2} = 9,0\,N}$ , dirigidas para direita e para cima.
- $\color{Navy}{F_{1} = – 15,0\,N}$ e $\color{Navy}{F_{2} = – 20,0\,N}$, dirigidas para esquerda e para baixo.
- $\color{Navy}{F_{1} = 30,0\,N}$ e $\color{Navy}{F_{2} = – 40,0\,N}$, dirigidas para direita e para baixo.
- $\color{Navy}{F_{1} = – 10,0\,N}$ e $\color{Navy}{F_{2} = 24,0\,N}$, dirigidas para esquerda e para cima.
Não esqueça de fazer contato por um desses canais em caso de dúvidas. Estou à disposição para ajudar.
Curitiba, 30 de março de 2015 (Revisado e atualizado em 20 de agosto de 2016)
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
