Física – Dinâmica – Leis de Newton

By decioadams in Física 18 de outubro de 2017

Imagens de Isaac Newton 4 — Imagen de Isaac Newton, mostrando refração da luz no prisma e alusão à maçã, que, segundo a lenda, inspirou a Segunda Lei da Mecânica. (Imagem repreduzida do Wikipedia)

Dinâmica

A física, ao longo da história da humanidade, desenvolveu-se em partes, por vezes parecendo desconectadas entre si e aos poucos se juntaram para formar um todo. Costumamos começar a estudar pelo assunto que teve um desenvolvimento mais precoce ao longo dos tempos. Trata-se da Mecânica. Não vamos aqui confundir com o trabalho das oficinas mecânicas. Elas fazem uso de conhecimentos de mecânica, para realizar seu trabalho na manutenção dos automóveis e demais máquinas.
A Mecânica, de modo simples, dizemos que estuda os movimentos e suas causas. Para simplificar, habitualmente dividimos em três partes: Estática, onde veremos o comportamento das forças em equilíbrio; a Cinemática, onde iremos analisar os movimentos, mas sem cogitar das causas de sua ocorrência e modificações; por último, a Dinâmica, quando iremos estabelecer as relações entre os movimentos e as forças. Essa divisão é apenas didática, pois não conseguiremos estudar tudo isso ao mesmo tempo. Temos que galgar um degrau de cada vez até chegar ao topo.

Nas últimas semanas, um programa de pesquisas do Google, o Trends, informou que ocorreu uma elevação da procura por temas relacionados à dinâmica em alto percentual. Por isso acho oportuno o momento para iniciar a escrever artigos falando do assunto. Tenho longos anos de experiência em sala de aula como professor e posso contribuir na elucidação, esclarecimento de dúvidas. Vou me dedicar a uma forma bem leve, partindo da suposição de que, aqueles que forem ler meus textos, são leigos, ou muito pouco versados nos assunto.

Quando me referi à divisão da Mecânica, falei em estabelecer as relações entre os movimentos e as forças. Vamos ser mais específicos agora. Tomemos por exemplo, você andando de bicicleta.
O que faz a bicicleta se movimentar?
A força que aplico no pedal, – será a sua resposta, com certeza.

Agora vejamos um atleta de salto em distância.

O que dá a ele o impulso para a realização do seus saltos?
Seus músculos, – será sua resposta.

Poderíamos passar muito tempo citando exemplos de forças que produzem ou modificam movimentos. O primeiro pesquisador a estabelecer equações matemáticas, que habitualmente chamamos de fórmulas, para os movimentos, foi Galileu Galilei.

Imagens de Galileu 3 — Imagem de Galileu, em seus últimos anos de vida.(Wikipedia)

A ele devemos as equações básicas dos movimentos retilíneos, tanto o uniforme, como o uniformemente variado.

Evangelista Torricelli, usou duas delas para estabelecer uma outra que relaciona apenas as velocidades e acelerações, sem o uso do fator tempo.

Imagem de Evangelista Torricelli 2 — Imagem de Evangelista Torricelli, que chegou a trabalhar como secretário de Galileu Galillei. (Wikipedia)

Imagem de Evangelista Torricelli 1 — Imagem de Evangelista Torricelli, inventor do barômetro de mercúrio. (Wikipedia)

No ano em que faleceu Galileu (1642), nasceu na Inglaterra Isaac Newton. Estudioso de matemática e física, descobriu haver entre os movimentos e as forças, algumas relações (equações) que poderiam ser aplicadas sempre, desde que as condições fossem as mesmas. É a base da Dinâmica Clássica, conhecida como Leis de Newton do Movimento. São em número de três.

1ª Lei de Newton:

Um corpo só modifica seu estado de movimento, repouso ou forma, se um sistema de forças de resultante não nula atuar sobre ele.

Isso quer dizer que, um corpo pode estar sob a ação de várias forças, mas se elas anularem mutuamente seus efeitos, o estado de movimento ou forma do corpo não se altera. Ele permanece indefinidamente nessa condição enquanto o sistema não for alterado. No momento em que um dos efeitos deixar de ser anulado, o corpo pode sofrer deformação ou entrar em movimento; adquirir aceleração, aumentando ou diminuindo a velocidade.

Essa lei também é conhecida como Princípio da Inércia, cujo enunciado é mais ou menos assim:

“Um corpo é incapaz de, por si só, alterar seu estado de movimento ou forma”.

Note que os dois enunciados são equivalentes e resultam nas mesmas consequências.

Para melhor entender o significado dessa lei, analisemos alguns exemplos. Falei antes de pedalar a bicicleta. Se você estiver num terreno plano e mantiver o movimento da bicicleta uniforme, estará aplicando uma força tal na bicicleta, suficiente para vencer a resistência do ar e o atrito das rodas com o chão. Já se estiver aumentando a velocidade, a força aplicada será de maior intensidade que as forças resistentes. Ao freiar, você não pedala, mas aciona os freios, fazendo uma força adicional no mesmo sentido das forças de resistência, que irão diminuir a velocidade.

O mesmo acontece com um automóvel. Quando você acelera o motor, soltando ao mesmo tempo a embreagem, começa a transmissão de força para as rodas e ele começa a se mover. Quanto mais você acelerar, maior será a velocidade que ele irá adquirir. Na descida, ou ao querer parar, o uso dos freios aplica uma força contrária para controlar a velocidade ou parar. Nota-se que sempre existe uma força resultante, no sentido da variação da velocidade. Se você puxar a extremidade de uma mola ou faixa elástica, haverá uma deformação. Ela será tanto maior quanto maior for a intensidade da força aplicada. Quando a força deixar de agir, o corpo volta ao seu comprimento inicial. A deformação se torna nula nesse caso.

3ª Lei de Newton:

Sempre que um corpo exerce uma força sobre o outro, esse outro exerce sobre o primeiro, uma força de mesma intensidade, mesma direção, porém de sentido contrário.

Obs.: Por que eu vou falar da terceira lei, antes da segunda? Note que nem uma nem outra resultam em uma equação, ou uma fórmula. São na verdade princípios que precisamos explicar, sem poder quantificar exatamente.

Vamos entender o que significa essa Lei. Quando pegamos uma mala pela alça e a erguemos do chão, notamos que nosso braço é puxado para baixo por uma força. É o que chamamos peso da mala. Para erguê-la do chão até a altura em que ela fica quando a carregamos, foi preciso aplicarmos uma força ligeiramente maior que o peso. No momento que ela para de subir, as duas forças passam a ser iguais. A que puxa nosso braço, é o peso da mala e nosso braço anula a ação dessa força, aplicando uma força de mesma direção, mesma intensidade e sentido contrário.

Quando um lutador de boxe acerta um direto de esquerda no queixo do adversário, ocorre a aplicação de uma força pelo punho do lutador, sobre o rosto do outro. A força de reação, é exercida sobre a mão do primeiro, pelo rosto do segundo. Poderíamos perguntar se não deveria ser empate o resultado da maioria das lutas. Como explicar que aquele que levou o direto, ficou tonto, podendo cair e mesmo perder a luta naquele momento? Ele pode cair e o juiz abre uma contagem, se não me engano até 5 ou 10. Se ele não conseguir ficar em pé nesse tempo, o juiz dá a vitória ao que desferiu o soco. Por quê os efeitos são tão diferentes?
Muito simples a resposta.

As forças são aplicadas em corpos diferentes e também em pontos diferentes.

A mão que desferiu o soco, é uma estrutura mais forte, tem os músculos e está preparada para o impacto. Já o queixo do adversário, é mais frágil, está ligado ao crânio e pode provocar um abalo no cérebro, deixando-o por alguns instantes sem condições de funcionar normalmente. As forças do par

Ação e Reação

, provocam efeitos dinâmicos diferentes por serem aplicadas a corpos diferentes. Por exemplo, o peso de um corpo. É a força com que a terra o atrai, pela gravidade. O corpo atrai a terra com uma força igual, mas as massas são tão diferentes que a terra nem se mexe, enquanto o corpo despenca do lugar onde estiver até a superfície da terra. As intensidades das forças são iguais, mas os efeitos bem diferentes, por causa das massas ou inércias dos corpos.

Até aqui falamos da inércia e das forças de ação e reação. Embora isso não nos tenha fornecido nenhuma fórmula ou equação para fazer cálculos, anote bem e não esqueça. Essas duas leis, a primeira e a terceira de Newton, são de fundamental importância.

2ª Lei de Newton:

A aceleração adquirida por um corpo, sob a ação de uma força resultante, é diretamente proporcional à intensidade da força e inversamente proporcional à massa do corpo.

Aplicando o raciocínio matemático a esse enunciado, podemos escrever que:

$$\bbox[4px,border:2px solid Olive]{\color{Navy}{a = {{F}\over{m}}}}$$

No SI (Sistema Internacional de Unidades) a aceleração é medida em $\color{Navy}{ m/s^2}$ e a massa em $\color{Navy}{kg}$ (quilograma). Podemos escrever a igualdade acima de forma mais linear. Basta multiplicar por $\color{Navy}{m}$ os dois membros da igualdade e inverter a ordem dos membros. Assim:

$\color{Brown}{\frac{F}{m}\times m = m\times a} $$\Leftrightarrow$$\color{Brown}{F = m\times a}$

A força resultante é igual ao produto da massa do corpo pela aceleração que ele adquire.

Podemos observar que nessa equação, quanto maior for a força aplicada em um corpo de massa $\color{Navy}{m}$ , maior será a aceleração que ele irá adquirir.

Para uma força resultante $\color{Navy}{F}$, aplicada a corpos de massas diferentes, quanto maior for a massa, menor será a aceleração.

Podemos observar isso nos automóveis que andam nas ruas. Ou nos carros de corridas que muitos de nós apreciam assistir pela TV. Quanto mais potência o motor tiver, isso é, mais força ele puder fornecer, mais o carro acelera e maior será a velocidade final.

Essa pequena expressão que Sir Isaac Newton nos legou, nos ajuda a resolver inúmeros problemas práticos de nosso cotidiano. Com certeza há mais coisas a serem levadas em conta, mas a base para a solução é essa pequena fórmula

Em função do que foi dito acima, a força no SI será então medida em:

$\color{Navy}{F = m\cdot a} \Leftrightarrow { F ={{ kg\cdot m}\over{s^2}} = newton(N)}$

Essa unidade foi batizada com o sobrenome do criador da lei. Por isso, no lugar de $\color{Navy}{{kg\cdot m}\over s^2}$, usamos apenas um $\color{Navy}{N}$. Se escrevermos a unidade por extenso, usamos apenas letras minúsculas, pois não é a pessoa, e sim a unidade que estamos citando.

Vejamos então como se faz a aplicação dessa lei. Seja o seguinte problema.

Um corpo de massa $\color{Navy}{{8,0}{ kg}}$ está apoiado sobre uma superfície perfeitamente lisa (sem atrito). Se sobre ele aplicarmos uma força resultante de intensidade $\color{Navy}{{20,0}{ N}}$, qual é a aceleração que ele adquire?
Obs.: um plano perfeitamente liso é algo que na prática não existe. Usamos essa idealização para raciocinarmos em condições que permitam aplicar a Lei sem considerar questões ainda não vistas.

Então:

$\color{Navy}{m = 8,0 kg}$
- $\color{Navy}{F = 20,0 N}$
- $\color{Navy}{F = m\cdot a}\Leftrightarrow{ a = {{F}\over {m}}}$
- $\color{Navy}{a = {{20,0}\over{8,0}} = 2,5\cdot{{ m}\over {s^2}}}$

O corpo irá adquirir uma aceleração $\color{Brown}{a = 2,5\,m/s^2}$ ou $\color{Brown}{a = 2,5\,m\times s^{-2}}$

Um corpo de massa $\color{Navy}{{25,0}{kg}}$, apoiado sobre um plano perfeitamente liso, adquire uma aceleração $\color{Navy}{a = 6,0 m/s²}$. Qual é a intensidade da força resultante que atua sobre ele?
- $\color{Navy}{m = 25,0 kg}$
- $\color{Navy}{a = 6,0 m/s²}$
- $\color{Navy}{F = m\cdot a}$
- $\color{Navy}{F = {25,0}\cdot{6,0} = 150,0}$N

A força resultante sobre o corpo é igual a $\color{Navy}{150,0 N}$.

Um corpo de massa $\color{Navy}{m}$ sofre a ação de uma força resultante $\color{Navy}{ F = 36,0\, N}$ e adquire uma aceleração $\color{Navy}{a = 4,0\, m/s^2}$. Qual é a sua massa? Supondo que esteja se movendo sobre um plano perfeitamente liso.
- $\color{Navy}{ F = 36,0\, N}$
- $\color{Navy}{ a = 4,0\, m/s^{2}}$
- $\color{Navy}{{F = m\cdot a}\Leftrightarrow {m = {{F}\over{a}}} }$
- $\color{Navy}{m = {{36,0}\over{4,0}} = 9,0\, kg}$

O corpo tem massa $\color{Navy}{m = 9,0\, kg}$.

Para exercitar um pouco, podemos deixar uns exemplos.

Um corpo tem movimento retilíneo e uniforme sobre um plano perfeitamente liso. Em dado momento começa a sofrer a ação de uma força contrária ao movimento. Sendo a intensidade da força igual a $\color{Brown}{F = 28,0\,N}$ e a massa do corpo de$\color{Brown}{m = 7,0\, kg}$, qual é a desaceleração que irá ocorrer?
Um corpo está apoiado em um plano horizontal perfeitamente liso, sob a ação de duas forças horizontais, de mesma direção, mas sentidos opostos. A primeira tem intensidade de $\color{Navy}{F_1 = 60,0\,N}$ e a segunda, oposta tem $\color{Navy}{F_2 = – 15,0\,N}$. A aceleração adquirida pelo corpo é de $\color{Navy}{a = 5,0\,m/s^2}$. Qual é a sua massa?
Um corpo de massa $\color{Navy}{m = 17,0\,kg}$, está apoiado em um plano perfeitamente liso e sofre um aceleração de $\color{Navy}{a = 3,2,m/s^2}$. Qual é a intensidade da força resultante atuando sobre ele?
Um corpo de massa igual a $m = 2,0\,kg$ move-se sobre um piso horizontal e sem atrito com velocidade inicial de $v_{0} = 36,0\,km/h$ quando submetido a uma força de $F= 4,0\,N$, durante um intervalo de tempo de $t = 3,0\,s$. Sobre o movimento desse corpo, determine:

a)A aceleração do corpo.

b)A velocidade do corpo ao final dos 3,0 s.

c)O espaço percorrido pelo corpo ao final dos 3,0 s.
Observe o sistema de blocos representado na figura abaixo. Os dois blocos da figura, de massas $m_{a} = 2,0\,kg$ e $m_{b}= 3,0\,kg$, movem-se juntos em razão de uma força externa de $F = 20,0\, N$, orientada da esquerda para a direita, exercida sobre o bloco A.

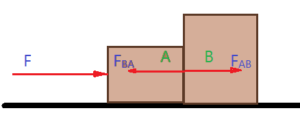
A respeito do sistema de corpos mostrado acima, determine:

a) A aceleração do conjunto.

b) A força que o bloco A exerce sobre o bloco B, $F_{AB}$.

c) A força que o bloco B exerce sobre o bloco A, $F_{BA}$.

d) Considerando que o sistema de blocos encontra-se inicialmente em repouso, calcule seu deslocamento após um tempo de 5,0 s. Desconsidere o tamanho dos blocos.

Uma pessoa necessita da força de atrito em seus pés para deslocar-se sobre uma superfície. Logo, uma pessoa que sobe uma rampa em linha reta será auxiliada pela força de atrito exercida pelo chão em seus pés.

Em relação ao movimento dessa pessoa, quais são a direção e o sentido da força de atrito mencionada no texto?

( )-a) Perpendicular ao plano e no mesmo sentido do movimento;

( )b) Paralelo ao plano e no sentido contrário ao movimento;

( )c) Paralelo ao plano e no mesmo sentido do movimento;

( )d) Horizontal e no mesmo sentido do movimento;

( )e) Vertical e no sentido para cima.

(IF-GO) – Um nadador, conforme mostrado na figura, imprime uma força com as mãos na água $F_{1}$ trazendo-a na direção de seu tórax. A água, por sua vez, imprime uma força no nadador $F_{2}$ para que ele se mova para frente durante o nado.

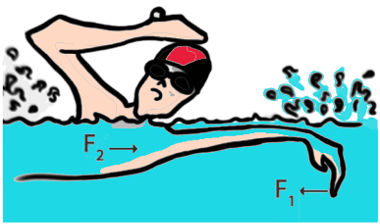
Assinale a resposta correta:

( )a) Esse princípio obedece à Lei da Inércia, uma vez que o nadador permanece em seu estado de movimento;

( )b) Obedecendo à Lei da Ação e Reação, o nadador imprime uma força na água para trás e a água, por sua vez, empurra-o para frente;

( )c) O nadador puxa a água e a água empurra o nadador, obedecendo à Lei das Forças (segunda Lei de Newton);

( )d) Nesse caso, é o nadador que puxa seu corpo, aplicando uma força nele próprio para se movimentar sobre a água;

( )e) O nadador poderá mover-se, pois a força que ele aplica na água é maior do que a resultante das forças que a água aplica sobre ele.

(UNIFICADO-RJ) – Dentro de um elevador, um objeto de peso $P=100\,N$ está apoiado sobre uma superfície. O elevador está descendo e freando com aceleração vertical e para cima de $a = 0,1\, m/s^{2}$. Considere a aceleração da gravidade como $g = 10\,m/s^{2}$ Durante o tempo de frenagem, a força que sustenta o objeto vale, em newtons:

( )a) 101;

( )b) 99;

( )c) 110;

( )d) 90;

( )e) 100.

(UEA) – Um objeto, que se desloca horizontalmente com velocidade $_{0}$, é submetido à ação de uma força constante de intensidade $F$ que o acelera, levando-o a atingir a velocidade $v$ em um intervalo de tempo $t$. Nessas condições, é correto afirmar que a massa do objeto vale:

( )a) $(v – v_{o}) ÷ F\times t$;

( )b) $F\times t ÷ (v – v_{o})$;

( )c) $F\times(v – v_{o}) ÷ t$;

( )d) $(F – v) ÷ v_{o}\times t$;

( )e) $v\times t ÷ (F – v_{o})$;

Analise as afirmações a respeito da inércia e marque a alternativa falsa:

( )a) A massa é a medida quantitativa da inércia;

( )b) Na falta de atrito, um corpo em movimento permanecerá em movimento perpetuamente;

( )c) A situação de movimento retilíneo uniforme é denominada de equilíbrio dinâmico;

( )d) A tendência de um corpo em movimento uniforme e com aceleração constante é manter-se em movimento perpetuamente;

( )e) O princípio da inércia é enunciado para corpos que estejam em repouso ou em velocidade constante.

Analise as afirmações feitas a respeito das leis de Newton.

I) É possível definir a segunda lei de Newton em função da quantidade de movimento.

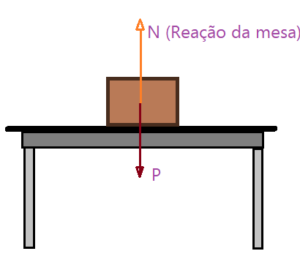
II) Um objeto depositado sobre uma superfície qualquer sofrerá a ação da força Normal como reação à força Peso.

III) A massa é a grandeza que representa a dificuldade imposta por um corpo à mudança de seu estado inicial.

IV) A unidade de medida para força é kg.m.s^{– 2}.

V) Ação e reação sempre possuem o mesmo sentido.

Marque a alternativa correta:

a) I e II são falsas

b) I, II, III e IV são verdadeiras.

c) IV e V são falsas

d) I, III e IV são verdadeiras.

e) III, IV e V são verdadeiras.

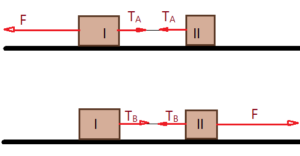
(UERJ – 2018) – Em um experimento, os blocos I e II, de massas iguais a $m_{I} =10\,kg$ e a $m_{II} = 6\,kg$, respectivamente, estão interligados por um fio ideal. Em um primeiro momento, uma força de intensidade $F = 64\,N$ é aplicada no bloco I, gerando no fio uma tração $T_{A}$. Em seguida, uma força de mesma intensidade F é aplicada no bloco II, produzindo a tração $T_{B}$. Observe os esquemas:

Desconsiderando os atritos entre os blocos e a superfície S, a razão entre as trações $\frac{T_{A}}{T_{B}}$ corresponde a:

( )a)$\frac{9}{10}$;

( )b)$\frac{4}{7}$;

( )c)$\frac{3}{5}$;

( )d)$\frac{8}{13}$;

( )e)$\frac{7}{13}$.

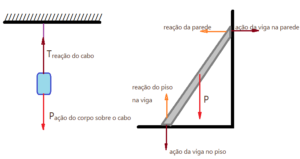
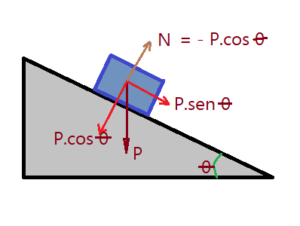
(Unigranrio – Medicina – 2017)Para manter um carro de massa 1000 kg sobre uma rampa lisa inclinada que forma um ângulo θ com a horizontal, é preso a ele um cabo. Sabendo que o carro, nessas condições, está em repouso sobre a rampa inclinada, marque a opção que indica a intensidade da força de reação normal da rampa sobre o carro e a tração no cabo que sustenta o carro, respectivamente. Despreze o atrito. Dados: $sen\theta = 0,6$; $cos\theta = 0,8$ e $g = 10\,m/s^{2}$.

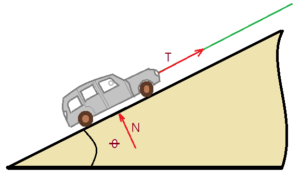
( )a) 8000 N e 6000 N;

( )b) 6000 N e 8000 N;

( )c) 800 N e 600 N;

( )d) 600 N e 800 N;

( )e) 480 N e 200 N.

(Cefet-MG) – Um veículo segue em uma estrada horizontal e retilínea e o seu velocímetro registra um valor constante. Referindo-se a essa situação, assinale (V) para as afirmativas verdadeiras ou (F) para as falsas.

( ) A aceleração do veículo é nula.

( ) A resultante das forças que atuam sobre o veículo é nula.

( ) A força resultante que atua sobre o veículo tem o mesmo sentido do vetor velocidade.

A sequência correta encontrada é

( )a) V F F.

( )b) F V F.

( )c) V V F.

( )d) V F V;

( )e)F F V.

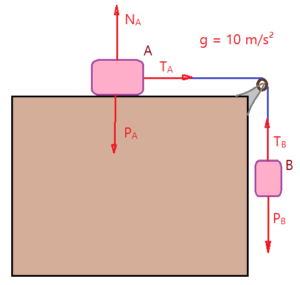
Dois corpos A e B, estão apoiados num plano horizontal perfeitamente liso e suspenso num cabo vertical passando por uma roldana, como mostra a figura. O corpo A tem massa de $m_{A}=50,0\,kg$ e o B tem massa de $m_{B}=20,0\,kg$. A aceleração da gravidade é $g=10,0\,m/s^{2}$. Determinar a aceleração do sistema e a intensidade das forças de tração $T_{A}$ e $T_{B}$.

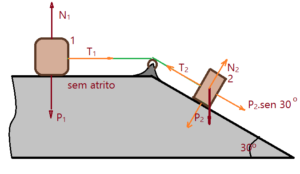
Um corpo está sobre um plano horizontal perfeitamente liso, ligado a outro sobre um plano inclinado de $\theta=30º$. A aceleração da gravidade local é de $g=10,0\,m/s^{2}$. As massas dos corpos são $m_{1}= 30,0\,kg$ e $m_{2}=40,0\,kg$. Determine a aceleração e seu sentido de deslocamento, bem como as trações nas cordas $T_{1}$ e $t_{2}$. Também se pede a determinação das forças de reação normal dos planos sobre os dois corpos respectivamente.

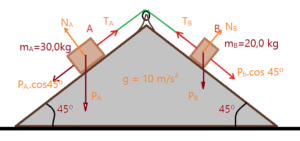
Um par de planos inclinados de $\theta = 45^{o}$, com dois corpos sobre os planos, perfeitamente lisos. Os corpos estão ligados entre si por um cabo que passa sobre uma roldana. Sendo a aceleração da gravidade local de $g=10,0\,m/s^{2}$. Determine a aceleração do sistema, o sentido de deslocamento, as trações nos cabos $T_{A}$ e $T_{B}$, as reações normais dos planos sobre os corpos $N_{A}$ e $N_{B}$.
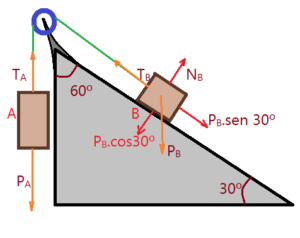
Um corpo está suspenso por um cabo, passando por uma roldana e ligado a outro corpo que está apoiado sobre um plano perfeitamente liso, inclinado de $\theta=30^{o}$. Sendo $g=10,0\,m/s^{2}$. As massas dos corpos são $m_{A}=30,0\,kg$ e $m_{B}=50,0\,kg$. Determinar os valores da aceleração, das trações nos cabos e a reação normal sobre o corpo B, pelo plano inclinado.
Obs.: Você certamente encontrará inúmeros exercícios semelhantes em qualquer local e se quiser entrar em contato comigo para tirar dúvidas, use um dos canais que vou listar abaixo. Estou à disposição para esclarecer o que ficar obscuro.