Física – Acústica, Som
Afinal, o que é o som?
O faz parte de nossa vida, desde antes de realmente nascermos. No interior do útero de nossa mãe, já conseguimos perceber os sons, especialmente os que ela emite e também o que ocorre ao seu redor. Não sou especialista para tecer comentários sobre o nível em que o feto percebe os sons, mas há sinais evidentes de que ele percebe.
Assim, nascemos e logo estamos rodeados de uma variedade enorme de sons, muitos dos quais não nos dizem nada e podem até mesmo nos amedrontar, outros despertar curiosidade, perplexidade e nem sei quantos outros sentimentos. Infelizmente(?) não guardamos registros claros sobre nossos primeiros anos de vida, salvo alguns raros flashes de algumas situações, principalmente as ligadas à visão e algumas aos sons.
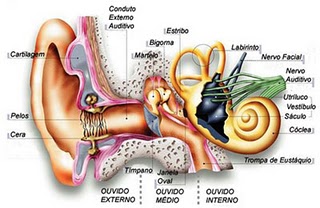
De ambos os lados de nossa cabeça somos providos de um órgão externo, o pavilhão auricular. Em alguns de nós ele é maior, outros menor, tudo dependendo das heranças genéticas que carregamos. O que sempre existe é uma pequena entrada, levemente escondida e protegida por um conjunto de pelos, cuja função é dificultar a entrada de algum inseto e principalmente poeira e outras impurezas. No caminho para o interior da caixa craniana, encontramos um pequeno tubo que via de regra é provido de uma espécie de “cera” e bem lá no fundo encontramos uma minúscula película, denominada “tímpano”, que funciona como uma membrana, capaz de vibrar. Ao ser atingida pelas vibrações trazidas pelas moléculas do ar, ela vibra na mesma frequência e seu contato com uma sequência de “ossículos”, o martelo, a bigorna e o estribo. Estes tem a função de levar as vibrações até os terminais nervosos do nervo auditivo, que por sua vez realiza a comunicação com a região do cérebro que interpreta essas vibrações, dando-nos a faculdade de ouvir. Faz parte do ouvido interno o chamado “labirinto” que tem a função de fornecer a noção de equilíbrio necessária para que possamos caminhar em linha reta, sem nos chocarmos com as coisas. Quando o labirinto é atingido por uma forma de inflamação, temos a chamada labirintite e a pessoa perde a noção de equilíbrio, sente náuseas e um mal-estar generalizado.
O que nos permite falar e emitir outros tipos de sons como gritar, assobiar, é o nosso aparelho fonador. No início da nossa garganta, localizam-se um par de membranas, denominadas “cordas vocais” que são postas em vibração pelo fluxo de ar proveniente dos pulmões. Essas vibrações podem receber diferentes modulações, bastando ajustar a cavidade bucal e vias aéreas superiores da forma correta.
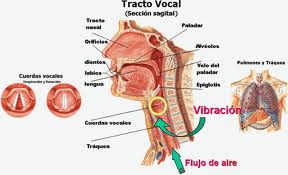
Isto nos permite formar os sons que nos dão a capacidade de falar e assim nos comunicar por meio de sons inteligíveis aos outros.
Como o som é produzido e se propaga?
Você deve estar se perguntando: Mas som é só isso? E os sons dos instrumentos musicais? Os ruídos de diferentes tipos que também ouvimos, de onde vem?
Ondas sonoras
Qualquer corpo, sólido, gasoso, líquido, maciço, fino e comprido, em forma de chapa, enfim todos são capazes de vibrar, mais ou menos intensamente, com maior ou menor frequência. Essas vibrações são comunicadas as moléculas vizinhas do próprio corpo e dos outros que estão próximos. Essa comunicação faz com que essas moléculas vibrem de uma forma característica, num movimento de “vai-vem”, que denominamos “onda mecânica longitudinal”. São essas ondas que levam o som até ao “tímpano” de nossos ouvidos e assim nós ouvimos os sons de diversas origens.
Ondas mecânicas
As ondas mecânicas se propagam nos meios materiais e dependem da capacidade das moléculas de vibrar. Elas não se propagam no vácuo. Podem ser transversais e longitudinais.
Ondas transversais: – são as ondas que se propagam numa direção e as moléculas do meio vibram numa direção perpendicular a de propagação. Você pode fazer uma experiência com uma bacia cheia de água e em repouso. Se deixar cair uma gota, ou uma semente qualquer no meio, irá observar uma perturbação da superfície que se propagará até a borda e depois irá retornar, extinguindo-se lentamente. Essa perturbação é um pulso de onda. Então imagine se esses pulsos forem repetidos a intervalos uniformes. Será formado um “trem de ondas”. Para não haver a onda refletida, pode-se forrar a borca com um pano ou camada de espuma. Veja a figura abaixo.
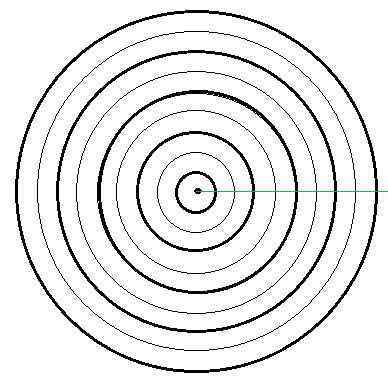

O trem de ondas nos mostra linhas mais fortes, alternadas com outras mais fracas. As primeiras representam os pontos mais altos denominados “cristas ou vértices” e as outras representam os pontos mais baixos das ondas, denominados “vales ou depressões”. A linha do meio representa a posição de equilíbrio da superfície. As partículas do líquido oscilam transversalmente a essa linha de equilíbrio. O tempo de uma oscilação de cada partícula é o período (T) da onda. No decorrer de um período a onda se desloca de uma distância igual à que existe entre duas cristas ou vales consecutivos. Esta distância é denominada comprimento de onda $\lambda$. Por um ponto podem passar $n$ cristas na unidade de tempo. Este número é denominado frequência.
Temos pois:
Frente de onda: – é a linha que separa a região ainda não perturbada do meio pela onda, da região já perturbada.
Crista ou vértice – é o ponto mais alto da onda.
Vale ou depressão – é o ponto mais baixo da onda.
Amplitude: – observando a forma da onda na figura acima, vemos que as partículas do meio oscilam de sua posição de equilíbrio até o ponto mais alto (crista) e depois desce até o ponto mais baixo (vale). Essa distância entre os extremos do movimento é denominado amplitude (A). Essa amplitude tem a ver com o nível de energia que a onda transporta no ponto. À medida que se afasta da fonte, a energia se dissipa no meio e espalha no meio. Com isso a amplitude gradualmente diminui. Esse fenômeno tem a ver, no caso das ondas sonoras, com a intensidade que o ouvido percebe.
Periodo (T): – é o tempo de uma oscilação completa das partículas do meio em que a onda se propaga. Medido em segundos $s$.
Frequência (f): – é o número de oscilações completas das partículas do meio, na unidade de tempo. Medida em hertz(Hz).
Comprimento de onda $\lambda$: – é a distância percorrida no decorrer de um período, ou seja, é a distância entre dois vales ou duas cristas consecutivas da onda, ou ainda entre dois pontos da onda que oscilam em fase, consecutivos.
Fase: – fase é o estágio do movimento de oscilação em que um ponto do meio se encontra em determinado instante, durante a propagação da onda. Os pontos que estão na mesma altura, oscilando no mesmo sentido, dizemos que estão em concordância de fase. Os pontos que estão na mesma altura, movendo-se em sentidos opostos, estão em oposição de fase. Assim duas cristas ou dois vales estão em concordância de fase. Já uma crista e um vale estão em oposição de fase. A distância que separa dois pontos em fase, é igual a um número inteiro de comprimentos de ondas($\Delta X = n\cdot\lambda$)
Ondas longitudinais: – a diferença fundamental entre esse tipo de onda e as demais, é que as partículas do meio em que se propagam vibram na mesma direção da propagação. O resto é igual. Isso cria regiões de compressão e regiões de rarefação do meio. Isto é na compressão as partículas ficam mais próximas entre si e na rarefação elas ficam mais afastadas. Na figura a seguir temos uma fonte sonora (alto-falante), emitindo um feixe de vibrações em uma determinada direção. As linhas mais juntas são os pontos de compressão e as linhas mais afastadas são os pontos de rarefação. As compressões correspondem às cristas e as rarefações aos vales.

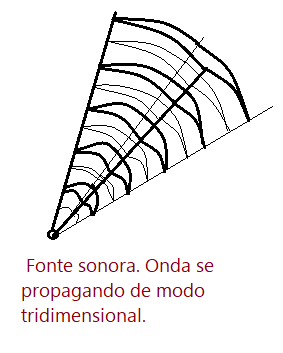
As ondas longitudinais, tem três grupos, formados por causa de suas frequências.
Infrassom: – são as ondas mecânicas longitudinais, com frequência entre $0$ e $20$ Hz. Há animais que são capazes de ouvir algumas frequências abaixo desse limite.
Som: – São todas as ondas dessa natureza entre as frequências $f = 20\, Hz$ e $f = 20000 Hz$. Há pessoas mais e menos sensíveis, mas os limites geralmente aceitos são esses.
Ultrassom: – de $20\, kHz$ até vários $GHz$ as ondas são ditas ultrassons. Essas ondas tem variadas aplicações industriais, especialmente em exames não destrutivos e não invasivos de peças industriais, em processos de limpeza, como atuantes em processos com reações químicas variadas.
| Seres vivos | Limite inferior (Hz) | Limite superior(Hz) |
| Humanos | 20 | 20000 |
| Cães | 15 | 50000 |
| Morcegos | 1000 | 120000 |
| Golfinhos | 150 | 150000 |
Velocidade: a velocidade de todas as ondas da família das mecânicas longitudinais é a mesma, nos mesmos meios. Vamos ver:
$\color{Brown}{V = \frac{\lambda}{T}}$
$\color{Brown}{V = \lambda\cdot f}$
A velocidade de uma onda mecânica varia em função das características físicas do meio em que se propaga. Para os meios gasosos temos uma fórmula, onde aparecem como influências elasticidade volumar $B$ e a densidade $\rho$, com esta expressão
$$\color{Blue}{V = \sqrt{\frac{B}{\rho}}}$$
Isto indica que a velocidade nos meios gasosos é diretamente proporcional à elasticidade e inversamente proporcional à densidade. No estudo dos gases vemos que a densidade deles decresce com a elevação de temperatura, explicando desse modo a elevação da velocidade das ondas sonoras com o aumento da temperatura.
Nos líquidos a velocidade é consideravelmente maior do que nos gases. Além disso a velocidade nos meios sólidos, aumenta com a “dureza” do material, como veremos na tabela a seguir.
Velocidades médias do som em meios sólidos
| Meio | Velocidade (m/s) |
| Vidro | 5130,0 |
| Alumínio | 5100,0 |
| Borracha | 54,0 |
| Chumbo | 1300,0 |
| Ouro | 3240,0 |
| Aço | 5940,0 |
| Diamante | 12000,0 |
| Meio | Velocidade (m/s) |
| Água$(20^{0}C)$ | 1493,0 |
| Água do mar | 1533,0 |
| Glicerina$(25^{0}C)$ | 1904,0 |
| Mercúrio | 1450,0d |
| Meio | Velocidade (m/s) |
| Hidrogênio $(0^{0}C)$ | 1286,0 |
| Hélio $(0^{0}C)$ | 972,0 |
| Ar $(20^{0}C)$ | 343,0 |
| Ar$(0^{0})$ | 330,0 |
Intensidade da onda sonora.
A onda sonora se propaga, a partir da fonte, em todas as direções. Na medida em que se afasta da fonte, a amplitude de oscilação das partículas do meio diminui. Como isso está diretamente ligado à intensidade que atinge o ouvido ou outros obstáculos que estejam no caminho, esta intensidade torna-se cada vez menos menor. Na medida que se afasta a mesma energia atinge uma superfície de onda cada vez maior e parte da energia é absorvida pelo meio em que se propaga.
$$\color{Blue}{ I = \frac{\Delta E}{A\cdot \Delta t}}$$
$$\frac{\Delta E}{\Delta t} = P$$\Rightarrow$ potência
$$\color{Blue}{ I = \frac{P}{A}}$$
Unidade: $$ I = \frac{W}{m^{2}} = W\cdot m^{-2}$$
Sensibilidade do ouvido humano
O pesquisador norte-americano Graham Bell, inventou o telefone e nas suas pesquisas para desenvolver os alto-falantes dos aparelhos acabou criando uma escala logarítmica que mede a sensibilidade do ouvido às diferentes intensidades das ondas sonoras. O crescimento da intensidade não é percebido na mesma proporção pelo ouvido. A expressão usada no cálculo é:
$$\beta = log\left(\frac{I}{I_{0}}\right)$$
Nesta expressão o $I_{0}$ é o menor nível audível, cujo valor é: $I_{0} = 10^{-12}\, W/m^{2}$
Para medir a sensibilidade usamos a unidade bel (B), em homenagem ao inventor do telefone e importante pesquisador.
Uma unidade bel é muito grande, tornando necessário o uso de uma fração decimal da mesma. Para isso multiplicamos a expressão logarítmica por um fator $10$.
$$\beta = {10,0}\cdot log\left(\frac{I}{I_{0}}\right)$$
Assim a unidade a ser usada é o decibel (dB).
$$ 1\,B = 10\, dB$$
Níveis de intensidade de diferentes sons
| Fonte sonora | Nível (dB) |
| proximidades de um jato | 150 |
| limiar de dor | 120 |
| sirenes em geral | 110 |
| aspirador de pó | 80 |
| mosca voando | 40 |
Em 1935 Charles Francis Richter e Beno Gutenberg desenvolveram a escala para medir a intensidade das ondas sísmicas dos terremotos, utilizada até os dias de hoje e conhecida como “Escala Richter”.
Com razoável aproximação pode-se usar, para determinar a velocidade do som no ar em diferentes temperaturas, a expressão:
$$V = 330,4 + 0,59\cdot\theta$$
Onde $\theta$ é medido em $^{0}C$.
| Temperatura ${^{0}C}|$ | Velocidade (m/s) |
| -10 | 330,0 |
| 0 | 332,0 |
| 10 | 337,0 |
| 20 | 343,0 |
| 30 | 350,0 |
| 100 | 390,0 |
| 500 | 550,0 |
| 1000 | 700,0 |
Eco
Quando a onda atinge um obstáculo, princialmente os rígidos e de dimensões razoáveis, ocorre o fenômeno da reflexão. A onda “bate” no obstáculo e retorna, ou muda de direção, causando o que denominamos eco. Tomando a velocidade média $V = 340,0 m/s$, podemos fazer a seguinte experiência.
Coloque-se à uma distância mínima, um pouco maior do que $17\, m$, e fale em alta voz uma palavra nítida. Você ouvirá o eco da última sílaba da palavra pronunciada. Isso ocorre por que o caminho de ida e volta do som será um pouco maior do que $34\, m$. Em média demoramos um décimo de segundo para emitir cada sílaba $\Delta t = 0,1 s$. Nesse tempo o som terá percorrido aproximadamente essa distância. Se você ficar a uma distância igual ao dobro, isto é, $34\,m$, irá ouvir o eco das duas sílabas finais aproximadamente. Assim por diante.
Se estamos em uma região montanhosa ou com diferentes obstáculos à frente, em diferentes posições e distâncias diferentes, poderemos ouvir ecos múltiplos de um mesmo som. Estando dentro de casa e passar pela rua um carro com um alto-falante a todo volume, iremos escutar o som, mas não de modo direto. Ele virá refletido em diferentes lugares até chegar aos nossos ouvidos.
Reverberação
É o fenômeno que ocorre em espaços fechados como igrejas, salões de festas, teatros ou outro ambiente qualquer. Acontece a reflexão do som nas pardes, colunas, no piso, no teto e em móveis, mas a distância não é suficiente para permitir a formação do eco de uma sílaba. Nestes casos ocorre uma sobreposição múltipla de reflexões ocorridas em diferentes distâncias, havendo pontos em que o som emitido em um outro ponto chega completamente distorcido. Isso é denominado reverberação. Para evitar esse inconveniente, os arquitetos e decoradores precisam prever a colocação de superfícies absorventes em quantidade suficiente para que a reflexão não ocorra ou pelo menos diminuir sua intensidade. Se esse fenômeno for convenientemente planejado e executado, a percepção do som torna-se muito melhor em todos os pontos do ambiente. Há exemplos de construções dessa natureza em que um palestrante, um cantor ou músico, postado em determinado ponto, sem uso de microfones para amplificação, é ouvido nítida e claramente em todos os lugares. Isso significa uma reverberação perfeita, que reforça o som em vez de confundí-lo, como muitas vezes acontece.
Qualidades fisiológicas do som
Um som possui, em função de suas grandezas físicas mensuráveis, algumas qualidades que estão ligadas ao modo como os ouvintes os percebem. Essas qualidades podem ter percepção diversa por diferentes ouvintes e recebem o nome de qualidades fisiológicas. A saber:
Altura; – é a qualidade que classifica o som em grave e agudo. Essa qualidade é determinada pela pela frequência de vibração das partículas do meio em que se propaga. A frequência é determinada pela fonte emissora e e constante para cada onda.
Intensidade: – é a qualidade associada à amplitude de oscilação das partículas do meio. A medição direta é mais complexa do que o nível sonoro calculado pela fórmula vista em tópico anterior. A unidade é decibel (dB). Essa qualidade se atenua na medida que o observador se afasta ou aproxima da fonte. Quanto maior a distância, menor é a intensidade.
Timbre: – o timbre permite distinguir dois sons de mesma altura e intensidade, mas emitidos por fontes diferentes, por causa de um conjunto de vibrações chamadas harmônicas que acompanham a onda principal. Você pode experimentar tocar duas notas de mesma altura em dois instrumentos como por exemplo um violão e um violino. Irá perceber que soam bem diferentes. É o timbre o responsável por isso. Cada pessoa tem seu próprio timbre de voz. Em geral somos capazes de reconhecer a pessoa que está falando em um lugar, apenas pelo timbre de sua voz. Logicamente há semelhanças nesse aspecto entre pessoas diferentes o que torna o processo impreciso.
Efeito Dopler
Imagine se você estiver parado à beira de uma rodovia, esperando um ônibus. Em dado momento ouve ao longe o som de um carro bastante ruidoso que se aproxima. Você irá notar duas modificações nas qualidades do som que ouve. Tanto a intensidade aumenta, pois o som chega com maior amplitude aos seus ouvidos. Mesmo ele não mudando nada na sua velocidade e emissão de ruido, você terá, no momento exato em que passa perto, a impressão de que trocou de marcha e o som parece ter diminuído de altura. Isso ocorre por uma razão muito simples.
Vimos que a $V =\lambda\cdot f$. Como o carro está em movimento, a distância fica menor a cada segundo, durante a aproximação. Com isso, o som emitido em dois instantes diferentes, percorre distâncias reais diferentes. Menores na aproximação e maiores no afastamento. Isso cria um comprimento de onda aparente, menor do que o real, o que para o ouvido do observador representa um aumento da frequência. Durante a aproximação, o som percebido é mais agudo do que o emitido pela fonte. No instante em que ele passa diante do observador a altura percebida é igual à emitida. Logo após fica mais grave, pois a frequência percebida fica menor. O comprimento aparente das ondas aumenta e a frequência parece diminuir. Isso se aplica em outras situações, referentes a qualquer forma ou tipo de onda. É de grande valor nos estudos astronômicos, movimentos de aproximação ou afastamento de estrelas, onde as diferenças de frequência representam mudanças de cor da luz. Na medicina temos cada vez mais aplicações, especialmente na obtenção de imagens de órgãos internos, tumores, fluxo sanguíneo e outras informações preciosas, sem que para isso seja necessário um procedimento invasivo, que sempre apresenta taxa de risco grandemente mais elevado do que esse método. Além desse mérito, existe outra vantagem nas imagens que o ultrassom fornece. A rapidez com que se alcança o resultado desejado, que é praticamente imediato.
A frequência do som percebido pelo observador quando a fonte ou tanto a fonte como o observador estiverem em movimento relativo entre si, é calculada pela expressão que segue.
$$ f_{O} = f_{F}\frac{V \pm V_{O}}{V \mp V_{F}}$$
Nesta expressão, temos:
$f_{O}$$\Rightarrow$ frequência percebida pelo observador.
$f_{F}$$\Rightarrow$ frequência da fonte emissora da onda.
$V_{O} $$\Rightarrow$ velocidade do observador em relação ao meio em que a onda se propaga.
$V_{F}$$\Rightarrow$ velocidade da fonte emissora em relação ao meio em que a onda se propaga.
Se o observador estiver imóvel na proximidade da trajetória da fonte sonora, temos que $V_{O} = 0$, e a expressão acima ficará:
$$\color{Blue}{f_{O} = f_{F}\frac{V}{V \mp V_{F}}}$$
Vejamos as ilustrações:


Observador percebendo a fonte se aproximando. Altura do som mais agudo. Depois que passa e se afasta, o som percebido fica mais grave.
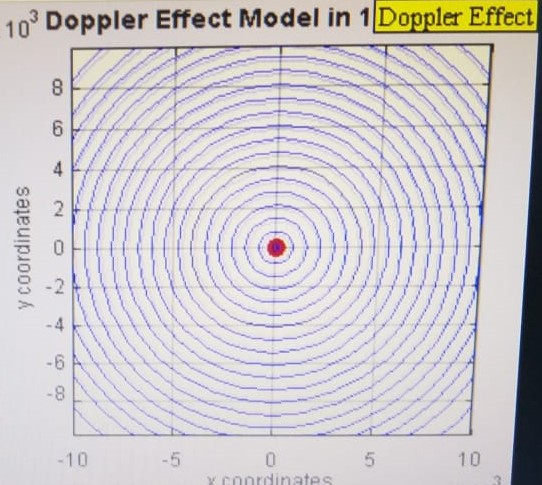
Uma fonte imóvel no meio irradia ondas com velocidade constante em todas as direções do meio, como vemos na figura.
Uma fonte irradiando ondas com velocidade constante, enquanto se movimente em uma direção do meio de propagação, mostra as ondas se “amontoando” na frente e se “espalhando” após a fonte.
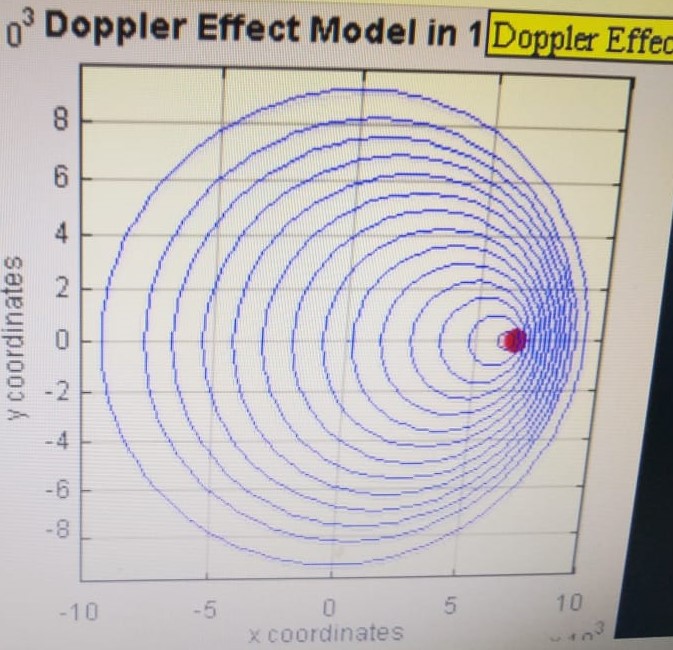
O observador à frente percebe som de maior frequência, enquanto um outro colocado atrás da fonte, perceberá uma frequência menor do que a emitida pela fonte. Observe a figura ao lado.
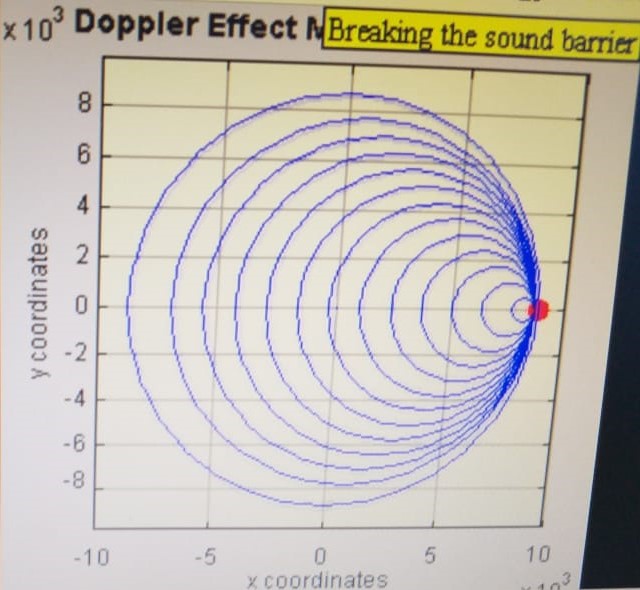
Quando a fonte passar a ter a velocidade do som, as ondas ficarão comprimidas em uma espécie de “barreira” que denominamos barreira do som. Um observador colocado à frente da fonte não irá ouvir som algum, pois as ondas não chegam a ele, antes da própria fonte.
Nesta condição temos que a velocidade da fonte $V_{F} = C$ e aplicando a fórmula vista teremos, para um observador no instante que a fonte passa por ele, a frequência:
$\color{Brown}{f_{O}= f_{F}\frac{C + 0}{C – C} = f_{F}\frac{C}{0} = \infty}$
Um outro observador colocado atrás da fonte, perceberá a frequência de:
$f_{O}= f_{F}\frac{C + 0}{C + C} = f_{F}\frac{\not{C}}{2\cdot\not{C}}$
$$\color{Brown}{f_{O} = \frac{1}{2}\cdot f_{F}}$$
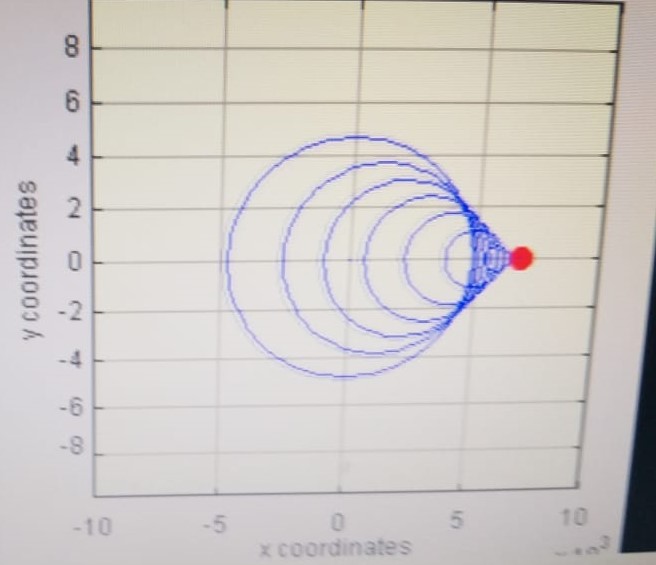
Quando a fonte sonora ultrapassa a velocidade do som dizemos que ele “quebrou” ou “rompeu” a barreira do som. Não existem ondas à frente da fonte (avião supersônico). O observador só irá perceber o som depois de ter sido ultrapassado pela fonte emissora, com uma frequência considerada negativa. Nesta situação temos que $V_{F}= k\cdot C$ e teremos, para o observador à frente da fonte:
$f_{O} = f_{F}\frac{C + 0 }{C – k\cdot C} = f_{F}\frac{C}{C\cdot(1 – k)}$
$$\color{Brown}{f_{O} = f_{F}\frac{1}{1 – k}}$$$\Rightarrow$$ k \gt 1$
Para um observador atrás da fonte, teremos:
$f_{O} = f_{F}\frac{C + 0}{C + k\cdot C} = f_{F}\frac{\not{C}}{\not{C}\cdot (1 + k)}$$\Leftrightarrow$$\color{Brown}{ f_{O}\lt f_{F}}$
Vamos exercitar um pouco esse conteúdo
01. Um estudante, após assistir a uma aula de Física sobre intensidade sonora, resolveu descobrir qual era o nível sonoro marcado na sala de sua casa quando o horário de tráfego de veículos na região onde mora é intenso. Um aplicativo de celular que simula um decibelímetro revelou que o nível sonoro era de $\beta=90 dB$. Sabendo que a intensidade mínima que corresponde ao limiar da audição humana corresponde a$I_{0}= 10 ^{-12}\, W/m^{2}$, determine a intensidade sonora referente à medida feita pelo garoto, em $W/m^{2}$.
$$\beta = 10\cdot log\left(\frac{I}{I_{0}}\right)$$
Para $I_{0} = 10^{-12}\, W/m^{2}$, $\beta = 90 dB$
$ 90 = 10\cdot log\left(\frac{I}{10^{-12}}\right)$
$\frac{90}{10} = log\left(\frac{I}{10^{-12}}\right)$
$9 = \frac{\logI}{\log10^{-12}}$
Fazendo $ I = 10^{n}$, teremos:
$9 = \frac{\log(10^{n}){\log(10^{-12})$$\Leftrightarrow$$9 = log(10^{n})\cdot (10^{12})$
$9 = n + 12$$\Leftrightarrow$$ 9 – 12 = n$
$n = -3$$\Leftrightarrow$$\color{Brown}{I = 10^{-3}\, W/m^{2}}$
02. (Cesgranrio) Quando a orelha humana é submetida continuamente a ruídos de nível sonoro superior a $\beta = 85 dB$, sofre lesões irreversíveis. Por isso, o Ministério do Trabalho estabelece o tempo máximo diário que um trabalhador pode ficar exposto a sons muito intensos. Esses dados são apresentados a seguir:
$\beta = 85\, dB$, $\Delta t = 8\, h$
$\beta = 90\, dB$, $\Delta t = 4\, h$
$\beta = 95\, dB$, $\Delta t = 2\, h$
$\beta = 100\, dB$, $\Delta t = 1\, h$
Observa-se, portanto, que a cada aumento de $5\, dB$ no nível sonoro, o tempo máximo de exposição cai para a metade. Sabe-se ainda que, ao assistir a um Show de Rock, espectadores próximos às caixas de som estão expostos a um nível sonoro de $110\, dB$. O nível de intensidade sonora $\beta$ é expresso em decibels (dB) por:
$$\color{Blue}{\beta = 10\cdot log\left(\frac{I}{I_{0}}\right)}$$
I = intensidade sonora fornecida pela caixa de som; $I_{0}$ = intensidade padrão, corresponde ao limiar da audição, para o qual $\beta = 0$. Para o nível de intensidade $\beta = 120\, dB$, a intensidade sonora, fornecida pela caixa de som, será:
$$\beta = 10\cdot log\left(\frac{I}{I_{0}}\right)$$
$120 = 10\cdot log\left(\frac{I}{I_{0}}\right)$
$\frac{120}{10} = \frac{I}{I_{0}}$$\Leftrightarrow$$ I = 10^{12}\cdot I_{0}$
03. Enem (2016) – As notas musicais podem ser agrupadas de modo a formar um conjunto. Esse conjunto pode formar uma escala musical. Dentre as diversas escalas existentes, a mais difundida é a escala diatônica, que utiliza as notas denominadas dó, ré, mi, fá, sol, lá e si. Essas notas estão organizadas em ordem crescente de alturas, sendo a nota dó a mais baixa e a nota si a mais alta. Considerando uma mesma oitava, a nota si é a que tem menor
a) amplitude
b) frequência
c) velocidade
d) intensidade
e) comprimento de onda
Como as notas estão em ordem crescente, a nota Si tem a frequência mais alta e por isso, terá o menor comprimento de onda. Isto indica que a resposta será a letra “e”.
04. Enem (2013) – Em um piano, o Dó central e a próxima nota Dó (Dó maior) apresentam sons parecidos, mas não idênticos. É possível utilizar programas computacionais para expressar o formato dessas ondas sonoras em cada uma das situações como apresentado nas figuras, em que estão indicados intervalos de tempo idênticos (T).
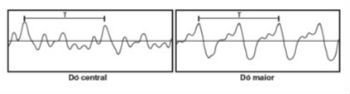
A razão entre as frequências do Dó central e do Dó maior é de:
a) 1/2
b) 2
c) 1
d) 1/4
e) 4
A diferença entre as duas notas é o que denominamos de “uma oitava” e significa que o Dó maior, tem o dobro da frequência do Dó central. Então a razão entre as frequências é $\frac{1}{2}$, da alternativa (a).
05. Determinada fonte produz ondas no ar com comprimento de onda igual a 2 mm. Assinale a alternativa que traz a informação correta a respeito dessas ondas.
Dados: Se necessário, adote a velocidade de propagação das ondas sonoras através do ar como sendo igual a 340 m/s.
a) As ondas sonoras são audíveis para o ser humano.
b) As ondas sonoras são inaudíveis, pois possuem frequência abaixo do valor mínimo perceptível pelo ouvido humano.
c) As ondas sonoras são inaudíveis, pois possuem frequência acima do valor máximo perceptível pelo ouvido humano.
d) As ondas sonoras são inaudíveis, pois o comprimento de onda é maior que a largura do tímpano.
e) Todas as alternativas estão incorretas.
Pelo cálculo da frequência obtemos que esta é $f = 170000Hz, o que nos mostra que as ondas não são audíveis para seres humanos. A resposta será pois a alternativa $c$.
06. Marque a alternativa correta a respeito das características das ondas sonoras.
a) Quanto menor for a densidade de um meio, maior será a velocidade do som, por isso as ondas sonoras propagam-se com maior velocidade no ar do que na água.
b) A altura é a qualidade do som relacionada à energia emitida pela fonte sonora.
c) Podemos diferenciar os sons de instrumentos musicais distintos, porque cada um produz som em uma frequência característica.
d) O aparelho auditivo humano é capaz de captar apenas um intervalo específico de frequências sonoras.
e) Um som alto significa um som de alto volume.
A alternativa correta é a letra $d$.
07. (Fac. Cultura Inglesa – SP) – A cuíca é um instrumento musical, semelhante a um tambor, com uma haste de madeira presa no centro de uma membrana de couro, pelo lado interno. Friccionando a haste com um pedaço de tecido molhado e pressionando a parte externa da cuíca com o dedo, produz-se uma onda sonora de ronco característico. Quando essa onda sonora propaga-se,
a) sua velocidade diminui:
b) sua amplitude aumenta:
c) há transporte de matéria:
d) aumenta a sua frequência:
e) há propagação de energia.
Toda onda transporta energia em sua propagação. Então a alternativa correta é $e$.
08. (UFSCar – SP) – Um homem adulto conversa com outro de modo amistoso e sem elevar o nível sonoro de sua voz. Enquanto isso, duas crianças brincam emitindo gritos eufóricos, pois a brincadeira é um jogo interessante para elas. O que distingue os sons emitidos pelo homem dos emitidos pelas crianças
a) é o timbre, apenas;
b) é a altura, apenas;
c) são a intensidade e o timbre, apenas;
d) são a altura e a intensidade, apenas;
e) são a altura, a intensidade e o timbre.
A alternativa correta é a letra $e$. Os adultos tem timbre diferente das crianças, suas vozes são naturalmente mais graves (altura) e se estão conversando calmamente sem alterar a voz e as crianças gritam, as intensidades também são diferentes.
Exercícios para treinar
01. Durante um jogo de futebol, a intensidade sonora é próxima de 80 dB. Supondo que, no momento do gol, a intensidade sonora torne-se 1000 vezes maior, qual é o valor do nível sonoro, em dB, no momento do gol?
a) 85 dB
b) 185 dB
c) 110 dB
d) 100 dB
e) 90 dB
02. Durante um show, a intensidade sonora nas proximidades do palco era de aproximadamente 1W/m2. Sabendo que a intensidade mínima para a audição humana é de 10 – 12 W/m2, determine o nível de intensidade sonora na região do palco:
a) 80 dB
b) 130 dB
c) 110 dB
d) 120 dB
e) 90 dB
03. (FUVEST) – O som de um apito é analisado com o uso de um medidor que, em sua tela, visualiza o padrão apresentado na figura a seguir. O gráfico representa a variação da pressão que a onda sonora exerce sobre o medidor, em função do tempo, em μs (1μs = 1 x10 – 6 s). Analisando a tabela de intervalos de frequências audíveis, por diferentes seres vivos, conclui-se que esse apito pode ser ouvido apenas por:
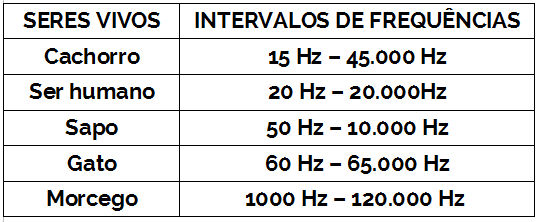
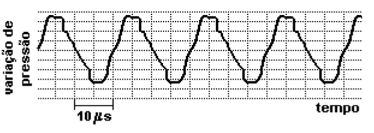
a) seres humanos e cachorros
b) seres humanos e sapos
c) sapos, gatos e morcegos
d) gatos e morcegos
e) morcego
Se houver dúvidas sobre o assunto, mesmo que sejam relativas a questões encontradas em outras fontes, não hesite em pedir ajuda. Estou à disposição para ajudar, esclarecer e até aprender junto.
Curitiba, 11 de maio de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
