Física – Ótica. Luz fenômeno ondulatório
Ondas em geral
Para analisar os fenômenos óticos, do ponto de vista ondulatório, recorremos às ondas mecânicas, que nos permitem visualizar os fenômenos, os elementos de uma onda, para então aplicar esses conhecimentos à ótica ondulatória.
Fonte puntiforme
Produz frente de ondas circulares.

Uma torneira gotejando, produz um trem de ondas circulares. Tem a mesma frequência, mesma velocidade e comprimento de onda. Cada gota ao cair produz um pulso de ondas. A sucessão de gotas em cadência resulta no trem de ondas.
Na figura as faixas claras representam as cristas da onda e as faixas escuras os vales ou depressões da onda. A curvatura da crista funciona com efeito de lente convergente, o que cria a diferença de luminosidade.
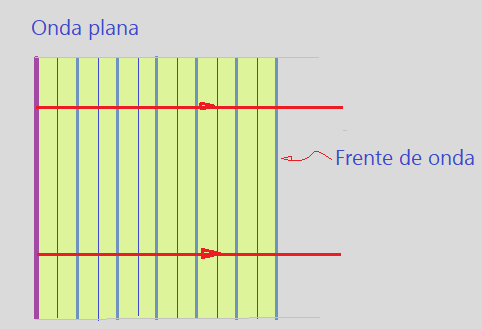
Fonte extensa linear
Um objeto extenso linear, produz um trem de ondas planas, como mostra a figura.
Reflexão de ondas
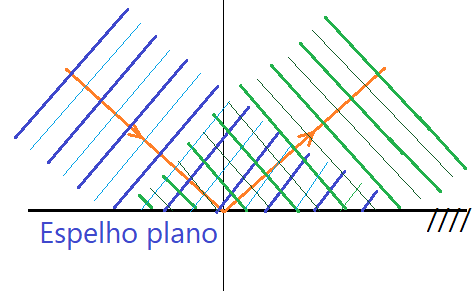
A onda refletida conserva as características da onda incidente, mudando sua direção. Como vimos na ótica geométrica, o ângulo de incidência e o de reflexão são congruentes. A reflexão produz inversão de fase, de modo a ocorrer a interferência construtiva e destrutiva em pontos alternados. Dessa forma surge o que chamamos de “onda estacionária”.
Refração das ondas
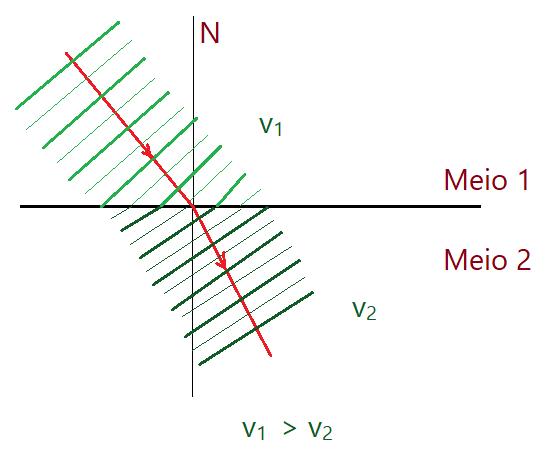
A onda passa de um meio transparente para outro, mudando a velocidade. Pode ser com aproximação em relação à normal ou afastamento.
1)Aproximação da normal. Passa do meio com maior velocidade para outro de menor velocidade.
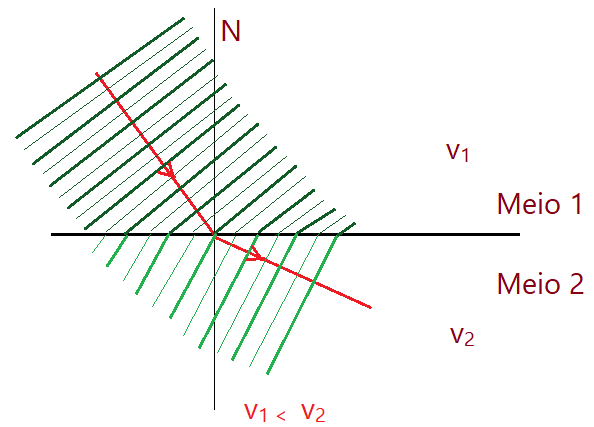
2)Afastamento da normal. A velocidade no meio de incidência é menor do que no meio de refração.
No primeiro caso ocorre uma redução de velocidade e consequentemente do comprimento de onda. Ocorre algo que se pode, a grosso modo, comparar a um veículo com freio desregulado, pegando mais de um lado que do outro. O veículo muda de direção para o lado que o freio está mais forte.
No segundo caso, ocorre o contrário. A velocidade aumenta e também o comprimento de onda. Imagine um automóvel subindo um desnível com piso liso(patina um pouco) e a partir de um ponto, um lado chega primeiro a uma parte com o piso mais aderente. Esse lado começa a andar mais depressa e a direção muda, para o lado que chega depois ao piso mais aderente.
Frente de ondas
Denominamos frente de ondas a linha reta ou curva que separa a parte do meio já perturbada pelo movimento ondulatório e a não perturbada.
Princípio de Huygens
Christiaan Huygens, defensor da teoria ondulatória da luz, apresentou um conceito que leva seu nome.
Cada ponto de uma frente de ondas funciona como uma fonte de ondas secundárias, cuja tangente é uma nova frente de ondas.
Difração de ondas

O Princípio de Huygens explica como uma onda consegue contornar um obstáculo que encontra em seu caminho, de modo a penetrar na região que seria de “sombra” e mesmo refazer a sua forma em algumas situações. Esse fenômeno é denominado difração. Veja a figura a seguir:
Obs.: Podemos de quebra observar nessa figura a reflexão da parte da onda não difratada. Ela volta interferindo com as ondas incidentes, formando franjas de interferência construtiva e destrutiva. Essas franjas formam o que chamamos de linha de nós ou linha de nodal. Nas regiões próximas ao obstáculo, a perturbação do meio fica pouco perceptível, pois a energia que ali chega é pouca.
Se usarmos uma fenda mais larga, a difração fica modificada. Uma pequena extensão das ondas tende a ficar reta, encurvando-se nas extremidades.


Franjas de interferência
Também chamadas de linhas nodais. Onde as ondas difratadas em duas fendas se encontram na mesma fase, suas amplitudes se somam e temos ali um ventre. Onde elas se encontram em oposição de fase, as amplitudes se subtraem e temos a formação de um nó.
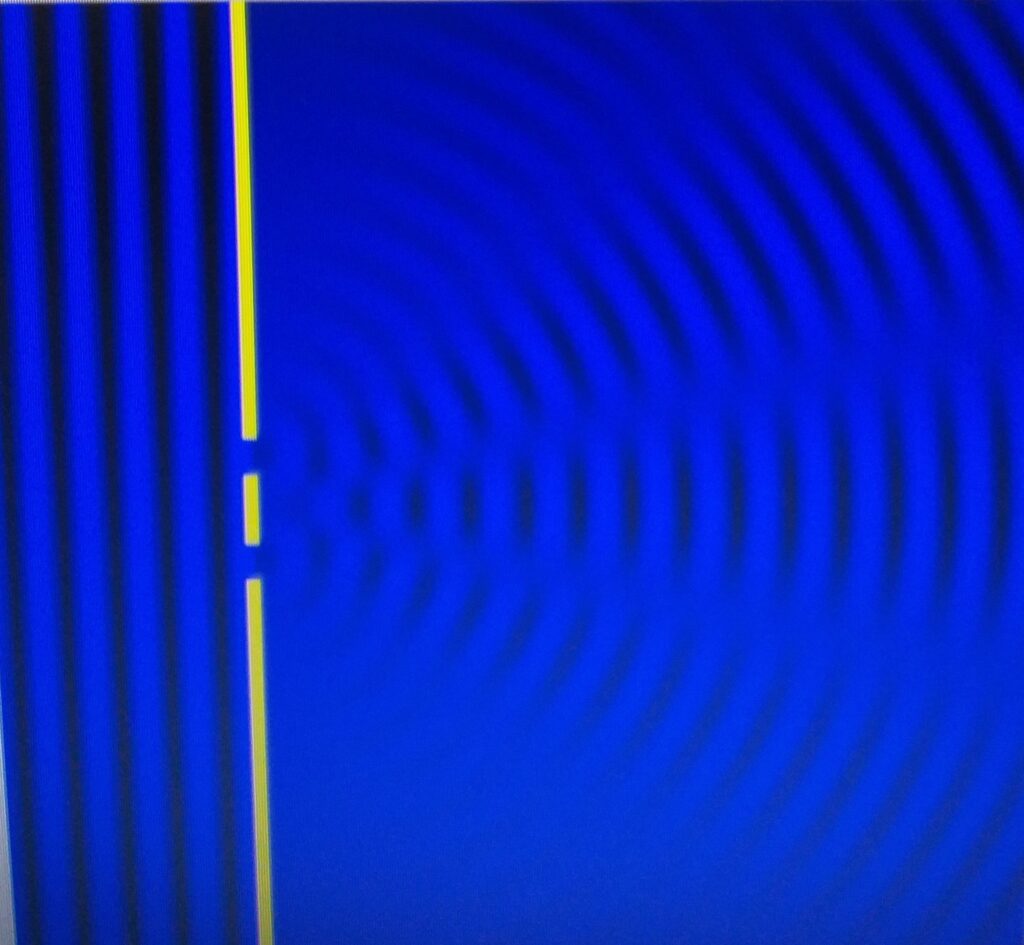
Notamos que as linhas nodais são nitidamente definidas, pois ali as ondas anulam mutuamente suas amplitudes. As linhas ventrais são mais extensas pois ali a amplitude resultante é maior. Nas bordas a esquerda e direita das fendas, existe uma região pouco perturbada.
Podemos obter essas franjas também com duas fontes geradoras de ondas coerentes, isto é, com a mesma frequência.
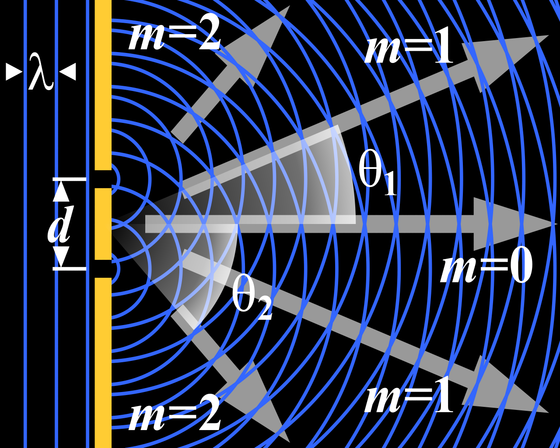
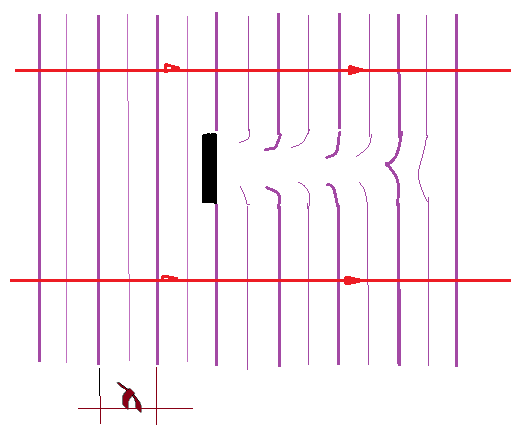
Se observarmos na figura acima e contarmos o número de comprimentos de onda de uma onda e da outra, desde a fenda até o ponto de interferência construtiva, veremos que há sempre a diferença de um número inteiro de comprimentos de onda nessa distância. Nos pontos de interferência destrutiva, haverá um número impar de meios comprimentos de onda.
Quando a diferença é de 1(um) comprimento de onda inteiro, temos a interferência de primeira ordem, depois segunda ordem com 2(dois) comprimentos de onda e assim sucessivamente.
Rede de difração
Podemos observar os efeitos de difração da luz com dispositivos simples, como encostar dois dedos de modo a ficar entre eles uma estreita fenda. Olhando para esta fenda, poderemos ver riscas claras e escuras, que são causadas pelo efeito da difração de todas as cores. As riscas claras são geradas pelas interferências construtivas das ondas luminosas e as escuras pelas destrutivas.
Um pedaço de tecido feito de fios finos e trama não excessivamente fechada, também fornece franjas de difração ao fazermos incidir sobre ele um feixe de luz. Um disco de CD, sem o lado opaco, permite passar a luz e os sulcos em que está gravada a informação, funcionam como fendas paralelas, ou seja como uma “rede de difração”.
Há, no mercado de materiais para laboratório de ciências, lâminas produzidas especialmente para esse fim, denominadas redes de difração. Em geral elas possuem entre 700 e 800 fendas por mm. Esse número é denominado “constante da rede”. Para usar esse número nos cálculos de experimentos é necessário determinar a medida da distância entre duas fendas consecutivas em $cm$ ou $m$. Ao final obtemos o valor de $\lambda$, comprimento de onda da radiação empregada no experimento. Em geral é expresso em $nm$. Esses cálculos exigem uso de geometria e trigonometria.
Imaginemos uma rede de difração, que contenha $720$ fendas por $mm$ e fazemos incidir sobre ela um feixe de luz branca. A uma distância $x$ da rede colocamos um anteparo translúcido para observar a franja de difração. A figura a seguir mostra esse experimento ampliado para efeito de raciocínio.
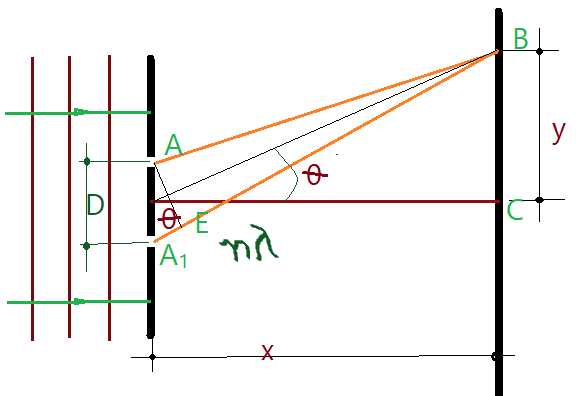
Se a rede de difração tem constante $k = 720$, significa que a distância $D$ entre duas fendas consecutivas será:
$1\,mm = 10^{-3}\,m$
$D = 1\frac{10^{-3}}{720}$$\Leftrightarrow$$D = 1,3889\times 10^{-6}\,m$
Temos uma pequena faixa central onde ocorre a interferência construtiva de todas as cores no mesmo lugar, de modo que ali a luz será branca. Na sequência encontramos uma faixa relativamente grande onde não há luminosidade. É a primeira região de interferências destrutivas, o que torna os pontos escuros.
A seguir aparece a primeira franja luminosa com as cores separadas, quando ocorrem as interferências construtivas. Como os comprimentos de ondas são diferentes, cada cor terá sua distância $y$, do centro até a franja.
Temos dois triângulos retângulos $\Delta AA_{1}EA$ e $\Delta ABCA$. O segmento $\overline{AE}$ pode ser considerado perpendicular ao segmento $\overline{A_{1}B}$, pois as diferenças são muito pequenas. O segmento $\overline{A_{1}E}$ representa um número inteiro de comprimentos de onda $n\lambda$. Essas aproximações são baseadas no fato de, para ângulos muito próximos de zero, o seno, a tangente e o ângulo terem aproximadamente o mesmo valor.
Sendo assim, teremos os ângulos $\widehat{A_{1}AE}$ e $\widehat{BAC}$ com a mesma medida.
$sen\theta = \frac{n\lambda}{D}$
$sen\theta = \frac{y}{\sqrt{x^{2} + y^{2}}}$
Igualando as duas expressões ficamos com:
$\frac{n\lambda}{D}= \frac{y}{\sqrt{x^{2} + y^{2}}}$
$\color{Navy}{n\lambda = \frac{D\times y}{\sqrt{x^{2} + y^{2}}}}$
Os valores de n são $\{n =1, 2, 3, 4,…\}$
Se observarmos a imagem formada no anteparo, teremos algo assim como mostra a figura.

Notamos que agora a ordem das cores está invertida se compararmos com a dispersão num prisma. A cor mais distante do centro é o vermelho, por ter o maior comprimento de ondas. Isso faz aumentar o cateto $y$ que indica a distância do feixe central ao feixe de interferência da cor. A figura mostra a franja de interferência de primeira ordem de ambos os lados. A próxima seria de segunda ordem, bem mais afastada do centro, uma vez que a diferença de percurso das fendas ao ponto de encontro será o dobro da primeira ordem.
Usando-se uma fonte luminosa de potência considerável, aproximando o anteparo da rede de difração consegue-se visualizar com alguma sorte até a terceira franja de interferência. Na figura a seguir, faço um esquema de formação de duas franjas de cada lado do eixo central, onde se forma a interferência sem diferença de percurso das ondas.
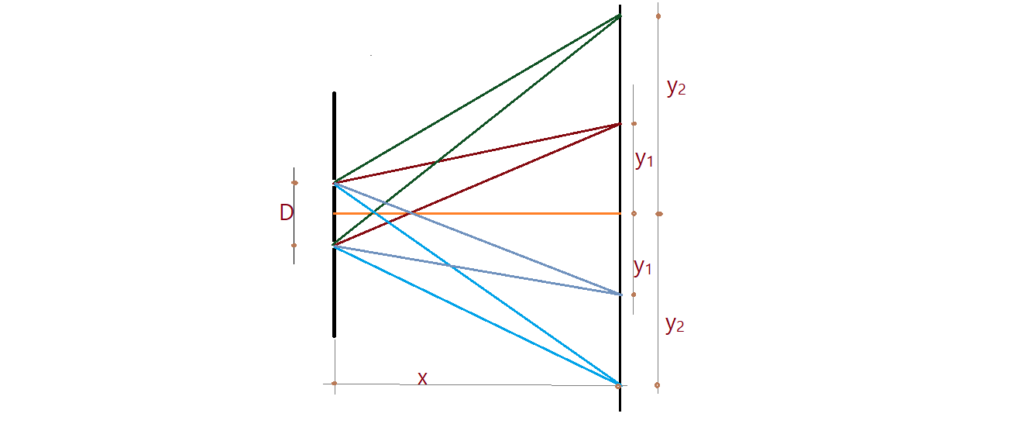
Exemplos.
01. Tomemos a rede de difração citada acima de $k=720\,fen/mm$, façamos incidir sobre ela um feixe de luz branca. Um anteparo colocado à distância $x = 1,0\,m$ serve de superfície de visualização das franjas de interferência. Determinemos o valor da distância $y$ para a onda vermelha de $\lambda =720\,nm$ e para a cor violeta de $\lambda = 400\,nm$, na primeira franja de interferência.
Se $k = 720\,fen/mm$$\Rightarrow$$D = \frac{1\times 10^{-3}}{720}$
$D= 1,389\times 10^{-6}\,m$
$\lambda_{ver} = 720\,nm$$\Rightarrow$$\lambda_{ver}=720\times 10^{-9}\,m$
$n\lambda = \frac{D\times y^{2}}{\sqrt{x^{2} + y^{2}}}$
$1\times 720\times 10^{-9} = \frac{1,389\times 10^{-6}\times y}{\sqrt{1 + y^{2}}}$
Elevamos ambos os membros ao quadrado para eliminar o radical do denominador.
${(720\times 10^{-9})}^{2} = \frac{(1,389\times 10^{-6}\times y)^{2}}{\sqrt{(1 + y^{2})^{2}}}$
$5,184\times 10^{-13} = \frac{1,929\times 10^{-12}y^{2}}{1 + y^{2}}$
$1 + y^{2} = \frac{1,929\times 10^{–12}\times y^{2}}{5,184\times 10^{-13}}$
$1 + y^{2} = 3,721y^{2}$$\Leftrightarrow$$ 1 = 3,721y^{2} – y^{2}$
$2,721y^{2} = 1$$\Leftrightarrow$$y^{2} = \frac{1}{2,721}$
$\color{Navy}{y = \sqrt{0,3675} = 0,606\,m = 60,6\,cm}$
$\lambda_{vio}= 400\,nm$$\Rightarrow$$\lambda_{vio}= 400\times 10^{-9}m$
$1\times 400\times 10^{-9} = \frac{1,389\times 10^{-6}\times y}{\sqrt{1 + y^{2}}}$
${(400\times 10^{-9})^{2}} = \frac{(1,389\times 10^{-6}\times y)^{2}}{\sqrt{(1 + y^{2})^{2}}}$
$1,6\times 10^{-13} = \frac{1,929\times 10^{-12}y^{2}}{1 + y^{2}}$
$1 + y^{2} = \frac{1,929\times 10^{-12}y^{2}}{1,6\times 10^{-13}}$
$1 + y^{2} = 12,056 y^{2}$$\Leftrightarrow$$1 = 12,056 y^{2} – y^{2}$
$11,056 y^{2} = 1$$\Leftrightarrow$$y = \frac{1}{11,056}$
$\color{Navy}{y = \sqrt{0,0904} = 0,301\,m = 30,1\,cm}$
02. Uma fração do feixe de luz branca que incide sobre uma rede de difração de $k = 750\,fen/mm$, tem frequência $f = 560\,THz$. Se o anteparo é colocado a distância $x$ da rede, determine o valor dessa distância para que a primeira franja de interferência dessa cor ocorra a $y = 25\,cm$ da franja branca central. Velocidade da luz no ar $v \simeq c =3\times 10^{8}\,m/s$
Sabemos que $ v = \lambda\times f$
$\lambda = \frac{v}{f}$$\Leftrightarrow$$\lambda = \frac{3\times 10^{8}}{560\times 10^{12}}$
$\lambda = 5,357\times 10^{-7}\,m$
Se $k = 750\,fen/mm$$\Rightarrow$$ D = \frac{1\times 10^{-3}}{750}$
$D = 1,333\times 10^{-6}\,m$
$n\lambda = \frac{D y}{\sqrt{x^{2} + y^{2}}}$
$1\times 5,357\times 10^{-7} = \frac{1,333\times 10^{-6}y}{\sqrt{x^{2} + {0,25}^{2}}}$
${(5,357\times 10^{-7})^{2}} = \frac{(1,333\times 10^{-6}\times{0,25})^{2}}{\sqrt{(x^{2} + 0,0625)}}$
$2,870\times 10^{-13} = \frac{1,777\times 10^{-12}\times{0,0625}}{x^{2} + 0,0625}$
$x^{2} + 0,0625 = \frac{1,110\times 10^{-13}}{2,870\times 10^{-13}}$
$x^{2} +0,0625 = 0,3868$$\Leftrightarrow$$x^{2} = 0,3868 – 0,0625$
$\sqrt{x^{2}} = \sqrt{03243}$$\Leftrightarrow$$x = 0,569\,m$
$\color{Navy}{x = 56,9\,cm}$
Hora de se divertir
01. Um feixe luminoso de cor azul, com comprimento de onda $\lambda = 480\,nm$, incide sobre uma rede de difração cuja constante é $k=780\,fen/mm$. O anteparo para projeção das franjas de interferência está colocado à $x=0,80\,m$ da rede. Determinar a distância da franja clara central até a franja de primeira e de segunda ordens.
02. Um feixe de luz de cor anil tem comprimento de onda $\lambda = 440\,nm$ e incide sobre uma rede de difração cuja constante é $k$. Se o anteparo está a $x = 1,0\,m$, formando a franja de primeira ordem à distância de $y = 40\,cm$. Determinar o valor da constante da rede.
03. Um fio fino, tem espessura de $D=2,5\times 10^{-5}\,m$ é usado para difratar um feixe de luz de cor anil, cujo comprimento de onda é $\lambda = 440\,nm$. Um anteparo é colocado a $x = 120\,cm$. Qual é a distância entre a franja central de interferência e a de primeira ordem?
04. Um feixe luminoso de cor laranja tem frequência $f= 510\,THz$ e se propaga com velocidade de $v = 3,0\times 10^{8}\,m/s$. Se incidirmos esse feixe luminoso sobre uma rede de difração $k=680\,fdn/mm$ e recebermos os feixes difratados sobre um anteparo colocado à $x = 75\,cm$ de distância. Qual é a posição da primeira e da segunda franja de interferência?
05. Qual é a cor da luz que, incidindo em uma rede de difração de $k = 720\,fen/mm$, forma sobre um anteparo posicionado a $x = 1,0\,m$ a franja de difração à $y = 48,0\,cm$ da franja central?
Se restarem dúvidas, faça contato por meio de um dos canais abaixo listados e lhe ajudarei em suas dificuldades.
Curitiba, 03 de novembro de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760 Celular e WhatsApp: (41) 99805-0732
