Física – Ótica física.
Ondas luminosas.
Segundo Isaac Newton a luz seria formada por um feixe de partículas ou corpúsculos, emitidos pelas fontes e que percorrem o espaço em altas velocidades. O grego Epícuro e depois Lucrécio, cerca de 100 a.C, faziam afirmação semelhante. Nessa teoria a velocidade da luz na água seria maior do que no ar. As cores seriam geradas pela perturbação que as partículas da luz causam no meio em que se propagam. Foi Isaac Newton o primeiro a realizar um experimento que resultou na decomposição da luz em sua várias cores. Havia em seu aposento, quando totalmente fechado, um fino feixe de luz solar que penetrava por um furo ou fresta. Não sei se proposital ou casualmente esse feixe incidiu sobre uma das faces de um prisma de vidro. O resultado foi que, ao atravessar a face ocorreu uma mudança de direção do feixe, originando um feixe levemente divergente. Dessa forma emergiu na segunda face um feixe com maior divergência e se formou num anteparo uma figura com as cores do arco-íris. A cor com menor desvio foi a vermelha, seguida da laranja, amarelo, verde, azul, anil e por último violeta.
Newton deixou esse fato registrado em livro, apenas não tinha uma explicação apropriada para o fenômeno. O que não ocorria com a teoria ondulatória. Era possível produzir ondas em uma superfície líquida, fazendo-a passar para outro meio diferente. A noção de frente de onda e ondas secundárias geradas por cada ponto atingido pela onda, permite explicar a mudança de direção por causa da variação de velocidade. A frequência da onda se conserva, mas o comprimento varia em cada meio. Com isso pode-se explicar a refração. Sendo a luz uma onda, o fenômeno é o mesmo, apenas as frequências muito mais altas e os comprimentos de onda bem menores.
Na mesma época de Isaac Newton, havia Christiaan Huygens e Robert Hook que defendiam a teoria ondulatória da luz. Cada uma das teorias explicava parte dos fenômenos inerentes à luz e sua propagação. Com o tempo a teoria ondulatória foi aperfeiçoada por Foucoult e outros estudiosos como Thomaz Young e Augustin Fresnel. O conceito de raio de luz foi estabelecido por Alhazen. Durante bastante tempo essa teoria predominou. Tinha a vantagem de ser mais fácil explicar os fenômenos da reflexão, refração e mesmo a difração por seu intermédio.
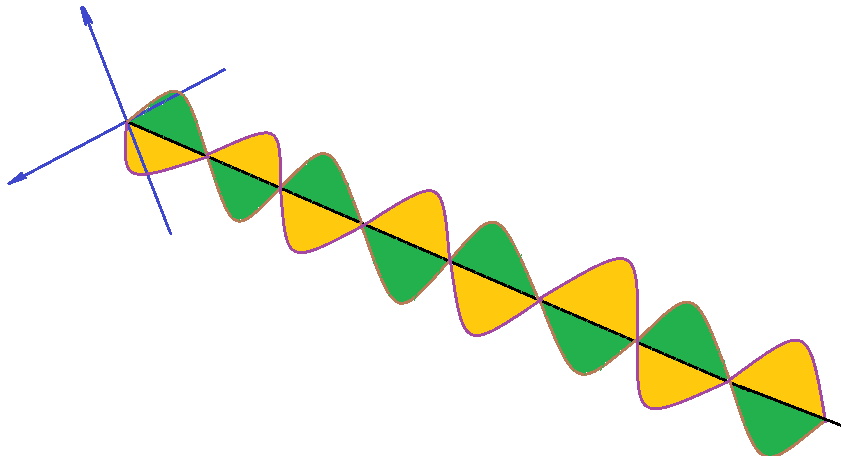
No século XIX James Maxwell, junto com a teoria das ondas eletromagnéticas em geral, considerou a luz como uma parte do espectro. Um campo elétrico e outro magnético, oscilam perpendicularmente em relação a uma linha de equilíbrio, transportando energia. Enquanto o campo elétrico varia no sentido positivo, o magnético varia no sentido inverso e assim alternadamente. Essas oscilações ocorrem em diferentes planos. São por isso ondas transversais não polarizadas. Max Planck introduziu a ideia de “pacotes” de energia, que vieram a ser chamados fótons e Albert Einstein em sua teoria da relatividade, uniu a teoria corpuscular, os fótons, com a teoria ondulatória.
Hoje sabemos que o espectro eletromagnético, ou seja, o conjunto de todas as radiações abrange desde os comprimentos de onda de algumas dezenas ou centenas de metros, até as radiações $\gamma$, com seus comprimentos de onda na ordem inferior aos $nm$ e suas frequências atingem a casa das potências $10^{24}\,Hz$.
A luz tem assim uma característica dual. É corpuscular da parte dos fótons e ondulatória em suas características de propagação geral. A emissão de fotons estabelece a harmonia entre as ondas eletromagnéticas e a teoria fotoelétrica.
Emissão de ondas eletromagnéticas
Ao estudar nas aulas de química o movimento dos elétrons na chamada eletrosfera de um átomo, vemos que essas partículas se movem em diferentes níveis de energia em órbitas diversas. Quanto mais distante do núcleo estiver a órbita, maior é o nível de energia do átomo. Há diversos fenômenos que podem deslocar um elétron de sua órbita estável para uma órbita mais elevada, isto é, ele recebe um quantum de energia e é empurrado para o nível superior. Esse deslocamento não é permanente. Na maior parte das vezes a permanência é muito curta, ocorrendo logo o decaimento para a órbita original. O que acontece com a energia que ele perde no decaimento? Essa energia é emitida sob a forma de um fóton de energia eletromagnética. Como as órbitas variam de uma substância para outra, seu nível de energia é diferente. O número de elétrons de cada átomo determina os diferentes níveis de energia e a quantidade deles que podem orbitar no mesmo nível.
Dissemos acima que o deslocamento dos elétrons para níveis mais altos de energia é causado por diferentes causas. Podemos distinguir alguns deles:
- Aplicação de corrente elétrica por meio de uma ddp. Os elétrons são catapultados pela energia fornecida para camadas mais elevadas. Ao decair, emitem diferentes fótons de energia radiante. Quando a temperatura atinge o ponto de incandescência, as radiações emitidas encontram-se parcialmente na faixa da luz visível. Diferentes formas de aquecimento produzem o efeito da incandescência, com emissão de radiações visíveis.
- Luminescência é um fenômeno de reação química que ocorre numa substância, sem variação significativa de temperatura. Este fenômeno pode ser de fosforescência como é o caso de alguns insetos em cujo organismo ocorrem determinadas reações emitindo luz visível. Ou alguns materiais que contem pequenas doses de fósforo em sua composição. Expostos à luz, sofrem “excitação” que depois é lentamente emitida, até esgotar a energia acumulada. Também temos a fluorescência, como é o caso das lâmpadas elétricas onde existe um vapor tênue de mercúrio no interior de um tubo de vidro. Ao submetê-lo a uma d.d.p. os elétrons das camadas exteriores são lançados para níveis mais altos e depois decaem. Ao interromper a corrente elétrica, cessa a emissão de luz. A radiação emitida pelo vapor de mercúrio é ultravioleta. Ao atingir uma camada de substância fluorescente nas paredes do tubo, ela provoca a emissão de luz visível.
Nesse fato de serem diferentes os níveis de energia dos elétrons temos a confirmação da emissão de variadas frequências de ondas eletromagnéticas. Experiências mais apuradas determinaram que qualquer corpo, à temperatura acima do zero absoluto, emite alguma forma de energia radiante. Quanto mais alta for a temperatura, maior será a variedade e principalmente as frequências das ondas que o corpo emite.
| Faixa de radiação | Comprimento de onda |
| Ondas de rádio | $10^{6}\, m => 1\,m$ |
| Micro-ondas (radar, fornos) | $1\,m => 10^{-4}\,m$ |
| Infravermelho | $10^{-4}\,m => 750\,nm$ |
| Luz visível | $750\,nm => 380\,nm$ |
| Ultravioleta | $380\,nm => 10^{-8}\,m$ |
| Raios X | $10^{-8}\,m => 10^{-12}\,m$ |
| Gaios gama | $10^{-12}\,m => 10^{-14}\,m$ |
| Cor | Frequências (THz) | Comprimento de ondas $nm$ |
| Vermelho | $400 – 484$ | $620 – 750$ |
| Laranja | $484 – 526$ | $590 – 620$ |
| Amarelo | $508 – 526$ | $570 – 590$ |
| Verde | $526 – 606$ | $495 – 570$ |
| Azul | $606 – 668$ | $450 – 495$ |
| Anil | $668 – 700$ | $428 – 450$ |
| Violeta | $700 – 789$ | $380 – 426$ |
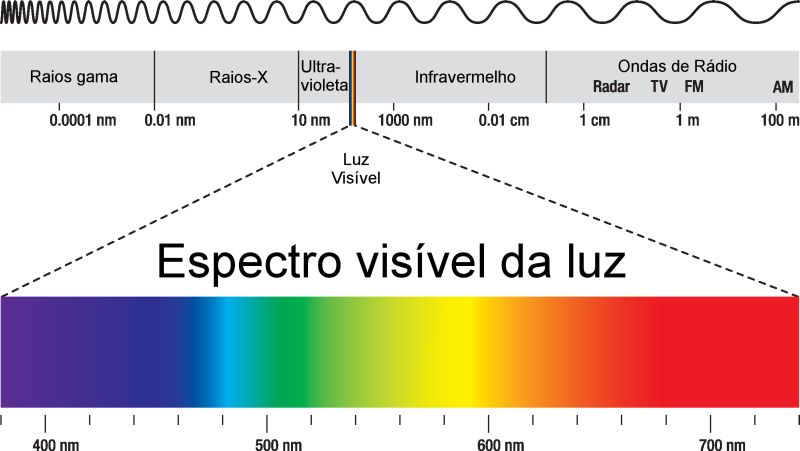
Pode-se notar que as radiações luminosas não são mais do que uma ínfima faixa do espectro eletromagnético. As cores são denominadas com o tom predominante na faixa, mas a transição de uma para outra ocorre gradualmente, como se elas fossem se misturando até atingir uma delas. Isso fica evidente se olharmos para a tabela anterior, onde cada cor corresponde a uma faixa de frequências.
Há algumas fontes que emitem mais radiação de uma cor do que de outras, de modo que ela se destaca no espectro. Isso depende da natureza da matéria e do efeito foto emissor em ação. Há fontes que emitem determinada faixa de frequências, caracterizando um feixe de luz quase monocromático, isto é, de uma única cor.
Equação da velocidade da luz
A velocidade da luz é calculada da mesma forma como calculamos a velocidade de uma onda mecânica, com a diferença de que uma tem comprimento e frequência diferentes da outra. As ondas mecânicas dependem da existência de um meio material elástico para se propagarem. Podem ser longitudinais e transversais. As ondas eletromagnéticas, entre elas a luz, se propagam melhor no vácuo do que em qualquer meio material. Assim:
$\color{Navy}{c = \frac{\lambda}{T} = \lambda\times f}$
Exemplo 1. Uma onda luminosa da cor verde, tem frequência $\color{Maroon}{f = 5,72\times 10^{14}\,Hz}$. Quando ela se propaga no vácuo a velocidade é $\color{Maroon}{c = 3,0\times 10^{8}\,m/s}$. Qual é o comprimento de onda desse feixe de luz? Qual é o período de oscilação dos campos elétrico e magnético?
Dados: $c = 3\times 10^{8}\,m/s$ e $f = 5,72\times 10^{14}\,Hz$
A fórmula que usamos é: $\color{Navy}{c = \lambda\times f}$
$3\times 10^{8} = \lambda\times 5,72\times 10^{14}$
$\lambda = \frac{3\times 10^{8}}{5,72\times 10^{14}}$
$\lambda = 5,24\times 10^{-7}\,m = 524\,nm$
$\color{Blue}{\lambda = 524\,nm}$
Sabemos que $f = \frac{1}{T}$$\Leftrightarrow$$T = \frac{1}{f}$
$T= \frac{1}{5,72\times 10^{14}}\simeq 1,75\times 10^{-15}\,s$
$\color{Blue}{T\simeq 1,75\times 10^{-15}\,s}$
Exemplo 2. Um feixe de luz violeta, tem $\color{Maroon}{\lambda = 408\,nm}$ e se propaga no vácuo. Determine o período de oscilação dos campos elétrico e magnético e a frequência de oscilação.
$\color{Maroon}{c = \frac{\lambda}{T}}$
$3\times 10^{8} = \frac{408\times 10^{-9}}{T}$$\Leftrightarrow$$T = \frac{408\times 10^{-9}}{3\times 10^{8}}$
$T = 1,36\times 10^{-15}\,s$$\Leftrightarrow$$\color{Navy}{T=1,36\times 10^{-15}\,s}$
$f = \frac{1}{T} = \frac{1}{1,36\times 10^{-15}} = 7,35\times 10^{14}\,Hz$
$\color{Blue}{f = 735\,THz}$
Exemplo 3. Um feixe de luz monocromático propaga-se no ar com velocidade $\color{Maroon}{v_{1}\simeq c}$. Atinge um dióptro em que sua velocidade se reduz a $\color{Maroon}{v_{2}=2,5\times 10^{8}\,m/s}$. Determine o índice de refração do meio que forma dioptro com o ar, calcule o comprimento de onda do feixe nos dois meios e seu período. Dada a frequência $\color{Maroon}{f=625\,THz}$.
Dados: $v_{1}\simeq c$; $v_{2}=2,5\times 10^{8}\,m/s$, $n_{ar}=1$ e $f=625THz$
$\color{Maroon}{n_{2}= \frac{c}{v_{2}}}$
$n_2= \frac{3\times 10^{8}}{2,5\times 10^{8}} = 1,2$
$\color{Navy}{n_2= 1,2}$
$\color{Maroon}{c = \lambda\times f}$
$\lambda = \frac{c}{f} = \frac{3\times 10^{8}}{625\times 10^{12}}$
$\lambda = 4,8\times 10^{-7}\,m$$\Leftrightarrow$$\color{Navy}{\lambda = 480\,nm}$
$\color{Maroon}{v_{2} = \lambda_{2}\times f}$
$\lambda_2 = \frac{v_2}{f} = \frac{2,5\times 10^{8}}{625\times 10^{12}}$
$\lambda_2 = 4\times 10^{-7}\,m$$\Leftrightarrow$$\color{Navy}{\lambda_2= 400\,nm}$
$\color{Maroon}{T = \frac{1}{f}}$
$T = \frac{1}{625\times 10^{12}} = 1,6\times 10^{-15}\,s$
$\color{Navy}{T= 1,6\times 10^{-15}\,s}$
Exemplo 4. Um raio luminoso partiu de uma estrela há um tempo de cinco anos e chega à terra nesse exato momento. Qual é a distância percorrida, supondo que não tenha sofrido desvios no percurso por quaisquer motivos?
Sabemos que um dia tem exatamente 86400\,s. Um ano tem 365 dias.
O tempo que esse raio luminoso está percorrendo o espaço é então de:
$ t = 5\times 365\times 86400 = 157680000\,s= 15,768\times 10^{7}\,s$
Sendo um MRU, usaremos; $\color{Maroon}{x = c\times t}$
$x = 3\times 10^{8}\times 15,768\times 10^{7}= 47,304\times 10^{15}\,m$
$\color{Navy}{x = 4,7304\times 10^{13}\,km}$
Obs.: Tomando o valor médio da ua (unidade astronômica), aproximadamente a distância da Terra ao Sol em média $150\times 10^{6}\,km$, podemos dividir o percurso desse raio luminoso por esse valor e encontraremos a distância medida nessa unidade.
$\color{Maroon}{x = \frac{4,7304\times 10^{13}}{150\times 10^{7}}}$
$\color{Navy}{x = 3,153\times 10^{5}\,ua}$
Exercícios para resolver.
01. Admitindo que o raio da Terra é igual a $\color{Maroon}{r = 6375\,km}$ no equador, qual é o tempo gasto por um raio luminoso para dar uma volta completa em torno do nosso planeta? $\color{Maroon}{C=2\times\pi\times r}$
02. Determine em quilômetros a distância percorrida pela luz no período de um ano.
03. Um feixe de luz azul, com frequência $\color{Maroon}{f= 640\,THz}$ propaga-se do ar $\color{Maroon}{n_{ar}=1}$ para uma lâmina de vidro, com uma redução de velocidade igual a $25\%$. Se o ângulo de incidência é igual a $\color{Maroon}{\hat{i}=30^{0}}$, determine: a) o comprimento de onda dessa radiação no ar; b) a velocidade do feixe no interior da lâmina de vidro; c) o ângulo de refração; d) o ângulo limite de incidência para essa radiação na face em que emerge da lâmina; e) o comprimento de onda da radiação no interior do vidro.
04. Um feixe de luz vermelha, com comprimento de onda de $\color{Maroon}{\lambda_{v} =720\,nm}$, propaga-se no ar e atinge a superfície da água, onde sua velocidade é de $\color{Maroon}{v_{2}=2,25\times 10^{8}\,m/s}$. Determine a frequência desse feixe azul, seu comprimento de onda no interior da água, o índice de refração da água para essa radiação.
05. Uma fonte emite luz amarela na frequência de $\color{Maroon}{f=520\,THz}$, no interior de um tanque cheio de água. Estando à uma profundidade de $\color{Maroon}{p = 2,0\,m}$, qual é o raio do círculo de luz que se consegue ver da beira do tanque? O índice de refração da água para essa luz amarela é $\color{Maroon}{n_{a} = 1,36}$. (Obs.: Lembre do ângulo limite de incidência e reflexão total interna).
06. Um raio de luz verde, tem comprimento de onda $\color{Maroon}{\lambda = 540\,nm}$ e se propaga no ar. Atingindo uma lâmina de faces paralelas, feita de vidro, cujo índice de refração para essa luz é $\color{Maroon}{n_{2}=1,16}$, numa direção de $\color{Maroon}{\hat{i}=36^{0}}$, qual será o desvio linear lateral sofrido depois de atravessar a lâmina cuja espessura é $\color{Maroon}{e = 8\,cm}$? Qual é a velocidade desse raio no interior da lâmina de vidro? Qual é seu comprimento de onda nos dois meios?
Se existirem dúvidas, faça contato por meio de um dos canais abaixo listados e providenciaremos o seu esclarecimento. Estou aqui para contribuir com seu desenvolvimento na área de física e matemática.
Curitiba, 15 de outubro de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
