FIME-020-01- Física – Mecânica – Dinâmica. Choque mecânico.
Choque mecânico ou colisão
Se dois corpos interagem, estando ao menos um deles em movimento e sua trajetória intercepta ou encontra a posição do outro, eles colidem ou se chocam mecanicamente.
As colisões podem ser de três tipos:
I – Elásticas – ocorre conservação da energia e do momento linear (quantidade de movimento).
II – Inelásticas – há dissipação de parte da energia, ficando os corpos juntos em movimento após a colisão. Há conservação apenas do momento linear.
III – Parcialmente elásticas – há perda de energia, mas em menor quantidade do que nas inelásticas e os corpos não permanecem juntos. Há conservação do momento linear.
Colisões elásticas
Os corpos se movem separadamente após a colisão e o sistema conserva a energia além do momento linear. Vejamos a ilustração.
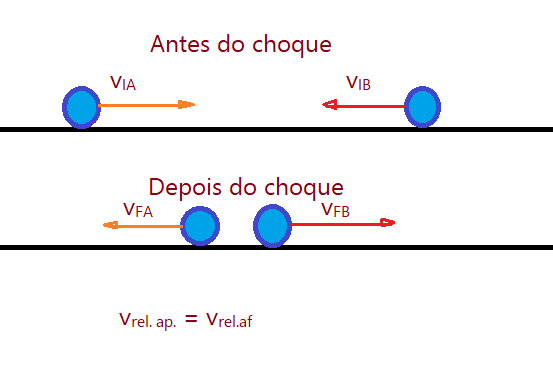
$$\color{Brown}{q_{i} = q_{f}}$$
$q_{iA} + q_{iB} = q_{fA} + q_{fB}$
$$\color{Navy}{m_{A}\times v_{iA} + m_{B}\times v_{iB} = m_{A}\times v_{fA} + m_{B}\times v_{fB}}$$
$$\color{Brown}{E_{i} = E_{f}}$$
$$\color{Navy}{\frac{m_{A}\times v_{iA}^{2}}{2} + \frac{m_{B}\times v_{iB}^{2}}{2} = \frac{m_{A}\times v_{fA}^{2}}{2} + \frac{m_{B}\times v_{fB}^{2}}{2}}$$
Colisões inelásticas (perfeitamente)
Corpos que se chocam e durante o fenômeno ocorre dissipação de energia em diferentes formas como calor, som, ou ruído. Os corpos se movem juntos como se ficassem “grudados” um ao outro. Vejamos a ilustração.
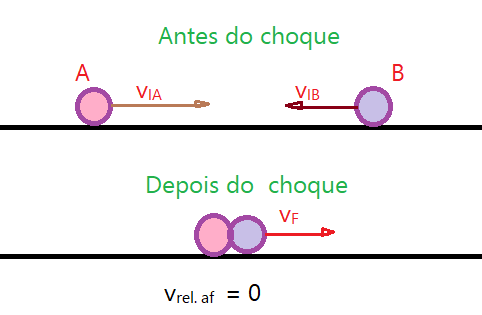
Nesse tipo de colisão ocorre conservação apenas do momento linear, sendo a energia dissipada parcialmente.
$$\color{Brown}{q_{i} = q_{f}}$$
$q_{iA} + q_{iB} = q_{fAB}$
$m_{A}\times v_{iA} + m_{B}\times v_{iB} = (m_{A} + m_{B})\times v_{fAB}$
$$\color{Navy}{v_{fAB} = \frac{m_{A}\times v_{iA} + m_{B}\times v_{iB}}{(m_{A} + m_{B})}}$$
Colisões parcialmente elásticas
É o tipo de colisão em que ocorre perda de parte da energia do sistema, mas é uma perda menor do que nos casos de colisões inelásticas. A velocidade relativa após o choque é menor do que antes do evento. Mesmo havendo perda de energia, o momento linear é conservado. Vejamos a ilustração.
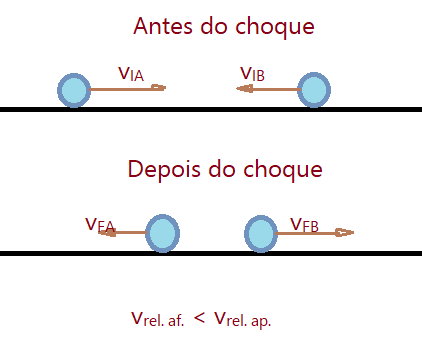
$$\color{Brown}{q_{i} = q_{f}}$$
$q_{iA} + q_{iB} = q_{fA} + q_{fB}$
$$\color{Navy}{m_{A}\times v_{iA} + m_{B}\times v_{iB} = m_{A}\times v_{fA} + m_{fB}}$$
O quociente das velocidades relativas afastamento pela de aproximação, fornece um número adimensional, compreendido entre zero e a unidade. esse número é o coeficiente de restituição.
$$\color{Navy}{e = \frac{v_{rel.af}}{v_{rel.ap}}}$$
O valor do coeficiente de restituição fica: $ 0\lt e \lt 1$
I- se $e = 1$$\Rightarrow$ a colisão é elástica.
II – se $e = 0$$\Rightarrow$ a colisão é inelástica.
III – se $0 \lt e \lt 1$$\Rightarrow$ a colisão é parcialmente elástica.
Colisões quanto às direções dos movimentos
Até aqui estivemos analisando colisões em que as velocidades dos corpos tem a mesma direção e são colineares. Isso significa que seus centros de massa estão alinhados e não existe força de interação que provoque movimento de rotação após o choque. Neste caso o choque é denominado unidimensional.
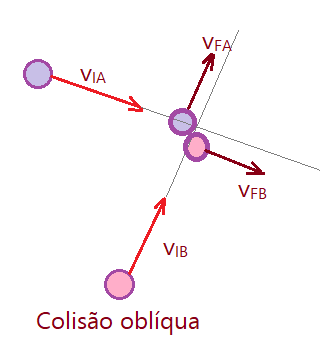
Se as velocidades dos corpos tiverem retas suportes concorrentes em um ponto e seus módulos forem tais que os centros de massa tendem a ocupar a mesma posição ao mesmo tempo, teremos um choque bidimensional ou oblíquo. Os movimentos ocorrem, antes e depois em um mesmo plano.
Se as retas que contém os vetores velocidade forem concorrentes, mas num sistema tridimensional, o choque ou colisão será também tridimensional.
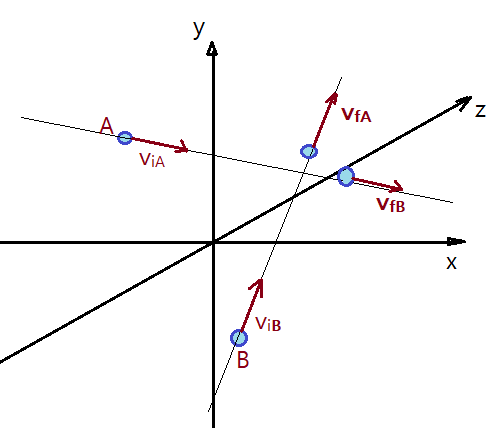
Quanto à elasticidade as características são as mesmas. Sendo grandezas vetoriais, o impulso e o momento linear podem ser decompostos em componentes no plano ou no sistema tridimensional e depois aplicamos a conservação da energia, momento linear e coeficiente de restituição.
Aplicando o conteúdo visto
01. Uma esfera rígida, de massa $\color{Sepia}{m_{1}=0,80\,kg}$, move-se com velocidade de $\color{Sepia}{v_{1} = 3,0\,m/s}$, aproximando-se de outra esfera semelhante, de massa $\color{Sepia}{m_{2}=0,50\,kg}$, que se move na mesma direção e em sentido oposto com velocidade $\color{Sepia}{v_{2}= – 4,0\,m/s}$. Sendo uma colisão perfeitamente elástica, determine as velocidades das duas esferas após a colisão. O choque é central ou frontal.
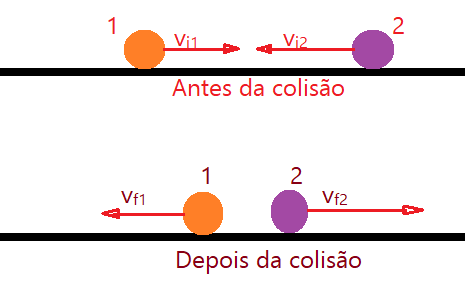
Conservação do momento linear.
$m_{1}\times v_{i1} + m_{2}\times v_{i2} = m_{1}\times v_{f1} + m_{2}\times v_{f2}$
$0,80\times 3,0 + 0,50\times {(-4,0)} = 0,40\times v_{f1} + 0,50\times v_{f2}$
$2,4 – 2,0 = 0,80\times v_{f1} + 0,50\times v_{f2}$$\Leftrightarrow$$0,4 = 0,80\times v_{f1} + 0,50\times v_{f2}$
Conservação da energia cinética.
$\frac{0,80\times v_{i1}^{2}}{2} + \frac{0,50\times v_{i2}^{2}}{2} = \frac{0,40\times v_{f1}^{2}}{2} + \frac{0,50\times v_{f2}^{2}}{2}$
$0,80\times {3,0}^{2} + 0,50\times {4,0}^{2} = 0,80\times v_{f1}^{2} + 0,50\times v_{f2}^{2}$
$7,2 + 8,0 = 0,80\times v_{f1}^{2} + 0,50\times v_{f2}^{2}$$\Leftrightarrow$$15,2 = 0,80\times v_{f1}^{2} + 0,50\times v_{f2}^{2}$
Isolando $v_{f}$ na equação anterior:
$0,50\times v_{f2} = 0,40 – 0,80\times v_{f1}$$\Leftrightarrow$$v_{f2} =\frac{0,40 – 0,80\times v_{f1}}{0,50}$
$v_{f2} = 0,8 – 1,6\times v_{f1}$
Substituindo na equação acima:
$15,2 = 0,80\times v_{f1}^{2} + 0,50\times {(0,8 – 1,6\times v_{f1})^{2}}$
$15,2 = 0,80\times v_{f1}^{2} + 0,50{(0,64 – 2,56 \times v_{f1} + 2,56\times v_{f1}^{2})}$$\Leftrightarrow$$15,2 = 0,80\times v_{f1}^{2} + 0,32 – 1,28\times v_{f1} + 1,28\times v_{f1}^{2}$
$2,08\times v_{f1}^{2} – 1,28\times v_{f1} + 0,32 – 15,2 = 0$$\Leftrightarrow$$2,08\times v_{f1}^{2} – 1,28\times v_{f1} – 14,88 = 0$
Aplicando Baskahra na equação do segundo grau:
$v_{f1} = \left(\frac{-(-1,28)\pm\sqrt{{(-1,28)}^{2} -4\times 2,08\times{(-14,88)}}}{2\times 2,08}\right)$$\Leftrightarrow$$v_{f1}= \left(\frac{1,28 \pm\sqrt{1,6384 + 123,8016}}{4,16}\right)$
$v_{f1}=\left(\frac{1,28\pm\sqrt{125,44}}{4,16}\right)$$\Leftrightarrow$$v_{f1}=\left(\frac{1,28\pm 11,2}{4,16}\right)$
$$\color{Brown}{v_{f1}= \left(\frac{1,28 + 11,2}{4,16}\right) = 3,0\,m/s}$$
$$\color{Maroon}{v_{f1}= \left(\frac{1,28 – 11,20}{4,16}\right) = – 2,385\,m/s}$$
Como estamos resolvendo uma equação do segundo grau, existem dois valores para a incógnita. Neste caso o primeiro valor, corresponde ao valor da velocidade do corpo $1$, antes do choque e o segundo é a velocidade com que ele retrocede após o choque. Vamos substituir na expressão que obtivemos acima e determinar a velocidade do corpo $2$.
$$\color{Maroon}{v_{f2} = 0,80 – 1,6\times v_{f1}}$$
$v_{f2} = 0,80 – 1,6\times 3,0 = 0,80 – 4,80 = -4,0\,m/s$
$v_{f2} = 0,80 – 1,6\times {(-2,385)} = 0,80 + 3,816 = 4,616\,m/s$
Desse modo temos que as velocidades após a colisão formam o par:
$$\color{Navy}{(v_{f1}; v_{f2})} = {(-2,385\,m/s; 4,616\,m/s)}$$
02. Uma esfera de $\color{Sepia}{m_{1}= 4,0\,kg}$, é atirada horizontalmente contra uma massa deformável e adesiva que se encontra sobre um carrinho em repouso, tendo massa total de $\color{Sepia}{m_{2}= 8,0\,kg}$. A esfera fica incrustada na massa, formando um único conjunto. Sendo assim, a colisão é perfeitamente inelástica e ocorre somente conservação da quantidade de movimento. Considerar a velocidade inicial da esfera $\color{Sepia}{v_{1} = 6,0\,m/s}$.
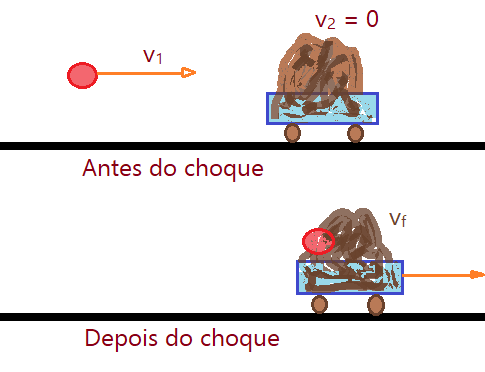
Temos que:
$$\color{Maroon}{q_{i} = q_{f}}$$
$q_{i1} + q_{i2} = q_{f12}$$\Leftrightarrow$$m_{1}\times v_{i1} + m_{2}\times v_{i2} = {(m_{1} + m_{2})}\times v_{f}$
$4,0\times 6,0 + 8,0\times {0} = {(4,0 + 8,0)}\times v_{f12}$$\Leftrightarrow$$v_{f12}= \left(\frac{24}{12}\right) = 2,0\,m/s$
$$\color{Navy}{v_{f12} = 2,0\,m/s}$$
03. Uma bola de bilhar, tem massa $\color{Sepia}{m_{1} = 50\,g}$ e move-se com velocidade de $\color{Sepia}{v_{1} = 2,0\,m/s}$, indo se chocar frontalmente com outra bola de mesma massa, que está em repouso sobre a mesa. Sendo o coeficiente de restituição igual a $\color{Sepia}{e = 0,9}$, determine as velocidades das duas bolas após o choque.
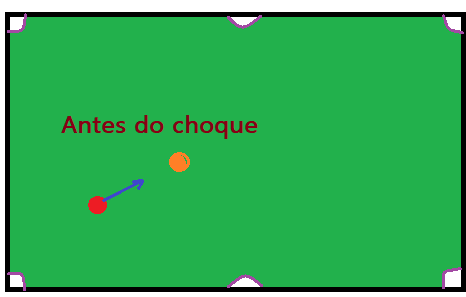
Sendo parcialmente elástico o choque, temos apenas conservação do momento linear do sistema. O coeficiente de restituição nos auxilia na resolução do problema.
$$\color{Maroon}{q_{i} = q_{f}}$$
$q_{i1} + q_{i2} = q_{f1} + q_{f2}$$\Leftrightarrow$$m_{1}\times v_{i1} + m_{2}\times v_{i2} = m_{1}\times v_{f1} + m_{2}\times v_{f2}$
Sendo as massas das bolas iguais, podemos cancelar esse fator na expressão inteira. A velocidade da bola $2$ antes da colisão é nula e por isso seu momento linear é nulo.
$\not{m_{1}}\times v_{i1} + \not{m_{2}}\times 0 = \not{m_{1}}\times v_{f1} + \not{m_{2}}\times v_{f2}$$\Leftrightarrow$$ 2,0 + 0 = v_{f1} + v_{f2}$
Sendo o coeficiente de restituição$ e = 0,90$, temos:
$$\color{Maroon}{e =\left(\frac{v_{af}}{v_{ap}}\right)}$$
$v_{ap}= 2,0 – 0 = 2,0\, m/s$
$v_{af} = v_{f2} – v_{f1}$
$0,90 = \left(\frac{v_{f2} – v_{f1}}{2,0}\right)$$\Leftrightarrow$$v_{f2} – v_{f1} = 2,0\times 0,90$
$v_{f2} – v_{f1} = 1,80$ (II)

Somando membro a membro as equações (I) e II), teremos:
$v_{f2} – v_{f1} = 1,80$
$v_{f2} + v_{f1} = 2,0$$
$2\times v_{f2} + 0 = 3,80\,m/s$$\Leftrightarrow$$v_{f2} = \frac{3,80}{2}$
$$\color{Navy}{v_{f2} = 1,90\,m/s}$$
Substituindo em uma das equações:
$v_{f1} + 1,90 = 2,0$$\Leftrightarrow$$v_{f1} = 2,0 – 1,9 = 0,10\,m/s$
$$\color{Navy}{v_{f1} = 0,10\,m/s}$$
Note que a bola $1$ ficou quase parada, enquanto a bola $2$, inicialmente em repouso, adquiriu uma velocidade quase igual à que animava a bola $1$. Se a colisão fosse perfeitamente elástica as velocidades simplesmente trocariam de bola.
04. Um automóvel $A$ se aproxima de um cruzamento ortogonal com velocidade de $\color{Sepia}{v_{A} = 72,0\,km/h}$ e tem massa de $\color{Sepia}{m_{A} =1600,0\,kg}$, enquanto outro automóvel $B$ de massa $\color{Sepia}{m_{B} = 1200,0\,kg}$, com velocidade de $\color{Sepia}{v_{B} = 90,0\,km/h}$ se aproxima do mesmo cruzamento num ângulo de $90^{0}$. Os dois julgam estar o cruzamento livre e avançam sem cuidado, ocasionando uma colisão. Qual é a velocidade final, logo após o choque? O choque nestes casos é inelástico, pois as deformações na lataria são permanentes, sem restituição. observe as ilustrações que seguem.
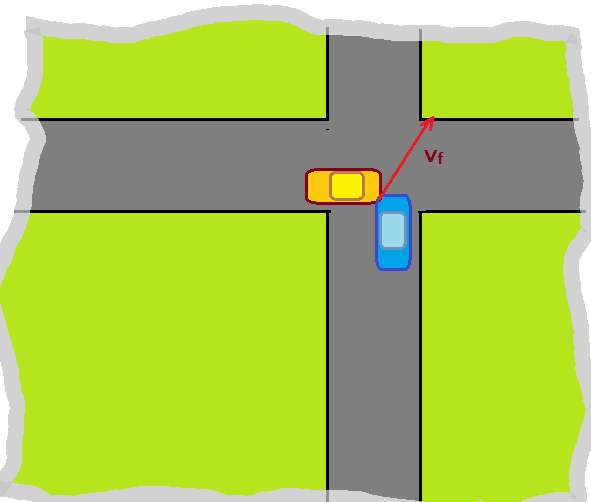
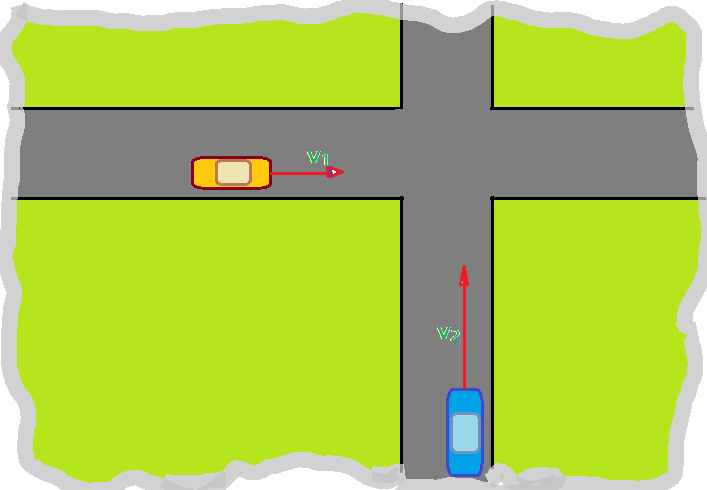
Sendo colisão inelástica, o coeficiente de restituição é nulo e ocorre conservação apenas do momento linear.
Sendo movimentos em direções diferentes, é necessário calcular o momento linear resultante pois é grandeza vetorial.
$v_{iA}= \left(\frac{72,0}{3,6}\right) = 20,0\,m/s$
$v_{iB}= \left(\frac{90,0}{3,6}\right) = 25,0\,m/s$
$$\color{Maroon}{q_{i} = q_{f}}$$
$q_{iA} =m_{A}\times v_{iA}$$\Leftrightarrow$$q_{iA} = 1600,0\times 20,0=32000,0\,kg.m/s$
$q_{iB}= m_{B}\times v_{iB}$$\Leftrightarrow$$q_{iB} = 1200,0\times 25,0 =30000,0\,kg.m/s$
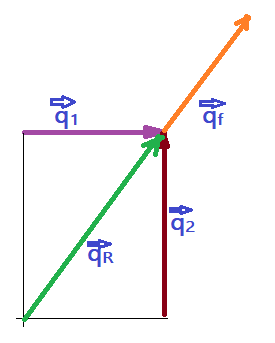
A figura representa os dois vetores momento linear antes da colisão, sua resultante e o momento final.
Resolveremos o problema pelo Teorema de Pitágoras, resultante de vetores ortogonais.
$q_{r} = \sqrt{q_{iA}^{2} + q_{iB}^{2}}$
$q_{r} = \sqrt{(3,2\times 10^{4})^{2} + 3,0\times 10^{4})^{2}}$
$q_{r} = \sqrt{(10,24 + 9,0)\times 10^{8}}$$\Leftrightarrow$$q_{r} =4,386\times 10^{4}\,kg.m/s$
Podemos escrever:
$q_{f} = q_{r}$$\Leftrightarrow$$(m_{A} + m_{B})\times v_{f} = 4,386\times 10^{4}$
$(1600,0 + 1200,0)\times v_{f} = 4,386\times 10^{4}$$\Leftrightarrow$$v_{f} = \left(\frac{4,386\times 10^{4}}{2800,0}\right)\simeq 15,664\,m/s$
Em $km/h$, teremos:
$$\color{Navy}{v_{f} = 15,664\times 3,6= 56,39\,km/h}$$
A direção pode ser determinada em relação a uma das vias que se cruzam. Vamos tomar para referência o caminho do automóvel A.
$tg\theta = \left(\frac{q_{iB}}{q_{iA}}\right) = \left(\frac{30}{32}\right) = 0,9375$
$\theta = arc tg (0,9375)$$\Leftrightarrow$$\theta\simeq 43,152^{0}$
$$\color{Navy}{\theta\simeq 43,152^{0}}$$
Para exercitar por conta
01. Um corpo de $\color{Sepia}{m_{1}=800,0\,kg}$ que se move a $\color{Sepia}{v_{1}=60,0\,m/s}$ colide com a parte de trás de outro corpo de $\color{Sepia}{m_{2} = 600,0\,kg}$ que se move a $\color{Sepia}{v_{2}= 40,0\,m/s}$, de forma que eles passam a mover-se juntos com velocidade de $\color{Sepia}{v_{f} = 35,0\,m/s}$. Sobre essa colisão, assinale a alternativa correta:
( )a) A colisão é elástica e, portanto, a quantidade de movimento do conjunto de corpos não sofre alteração;
( )b) A energia cinética do sistema de corpos sofre um acréscimo após a colisão;
( )c) Trata-se de uma colisão não conservativa, na qual a quantidade de movimento do sistema é conservada em cerca de 49 000 kg.m/s;
( )d) Trata-se de uma colisão conservativa, na qual a quantidade de movimento do sistema é conservada em cerca de 49 000 kg.m/s;
( )e) Trata-se de uma colisão não conservativa, na qual a quantidade de movimento do sistema é reduzida em cerca de 23 000 kg.m/s.
02. Duas bolas de bilhar de massas iguais a $\color{Sepia}{m = 30\,g}$ cada, movendo-se uma em direção à outra com velocidade de $\color{Sepia}{v =10,0\,m/s}$, colidem, invertendo o sentido de movimento com a mesma velocidade. Sobre essa colisão, assinale a alternativa correta:
( )a) Parte da energia cinética do sistema é perdida durante a colisão, caracterizando-se, assim, como uma colisão inelástica;
( )b) A colisão referida é parcialmente inelástica, já que uma parte da quantidade de movimento do sistema é perdida;
( )c) A quantidade de movimento do sistema permanece constante, já que a colisão entre as bolas de bilhar é perfeitamente elástica;
( )d) A colisão referida no enunciado é perfeitamente inelástica;
( )e) A colisão referida no enunciado é parcialmente inelástica.
03. Um corpo A de massa $\color{Sepia}{m_{A}=10,0\,g}$ move-se sobre uma superfície lisa e horizontal com velocidade de $\color{Sepia}{v_{iA}=4,0 \,m/s}$ e colide com um corpo B de massa $\color{Sepia}{m_{B}=20,0\,g}$ que se encontra em repouso. Após a colisão, o corpo A retrocede, movendo-se com velocidade de $\color{Sepia}{v_{fA}=1,0\,m/s}$. A velocidade do corpo B em $m/s$, após a colisão, é igual a:
( )a) 2,5 m/s;
( )b) 3,5 m/s;
( )c) 4,0 m/s;
( )d) 3,0 m/;
( )e) 2,0 m/s.
04. Dois patinadores de massas iguais a $\color{Sepia}{m_{1}=60,0\,kg}$ e $\color{Sepia}{m_{2}=80,0\,kg}$, inicialmente em repouso sobre uma pista de gelo lisa e livre de atritos, empurram-se mutuamente. O patinador de $\color{Sepia}{m_{A}=60,0\,kg}$ move-se para a esquerda com velocidade de $\color{Sepia}{v_{iA}=3,0\,m/s}$ após o empurrão. Qual é a velocidade adquirida pelo segundo patinador?
( )a) 3,50 m/s;
( )b) 3,25 m/s;
( )c) 2,25 m/s;
( )d) 0,65 m/s;
( )e) 0,80 m/s.
05. Quando uma pessoa dispara uma arma vemos que ela sofre um pequeno recuo. A explicação para tal fenômeno é dada:
( )a) pela conservação da energia;
( )b) pela conservação da massa;
( )c) pela conservação da quantidade de movimento do sistema;
( )d) pelo teorema do impulso;
( )e) pelo teorema da energia cinética.
06. Supondo que uma arma de massa $\color{Sepia}{m_{a}=1\,kg}$ dispare um projétil de massa $\color{Sepia{m_{p}=10\,g}$ com velocidade de $\color{Sepia}{v_{p}=400\,m/s}$, calcule a velocidade do recuo dessa arma.
( )a) -2 m/s;
( )b) -4 m/s;
( )c) -6 m/s;
( )d) -8 m/s;
( )e) -10 m/s.
07. Um carrinho de massa $\color{Sepia{m_{1} = 2,0\,kg}$, deslocando-se com velocidade $\color{Sepia}{v_{1} = 6,0\,m/s}$ sobre um trilho horizontal sem atrito, colide com outro carrinho de massa $\color{Sepia}{m_{2} = 4,0\, kg}$, inicialmente em repouso sobre o trilho. Após a colisão, os dois carrinhos se deslocam ligados um ao outro sobre esse mesmo trilho. Qual a perda de energia mecânica na colisão?
( )a) 0 J;
( )b) 12 J;
( )c) 24 J;
( )d) 36 J;
( )e) 48 J.
08. (FUVEST) – Uma partícula se move com velocidade uniforme V ao longo de uma reta e choca-se frontalmente com outra partícula idêntica, inicialmente em repouso. Considerando o choque elástico e desprezando atritos, podemos afirmar que, após o choque:
( )a) as duas partículas movem-se no mesmo sentido com velocidade V/2;
( )b) as duas partículas movem-se em sentidos opostos com velocidades – V; e + V;
( )c) a partícula incidente reverte o sentido do seu movimento, permanecendo a outra em repouso;
( )d) a partícula incidente fica em repouso e a outra se move com velocidade v;
( )e) as duas partículas movem-se em sentidos opostos com velocidades – v e 2v.
09. Um pêndulo balístico é composto de um bloco de madeira, de massa $\color{Sepia}{m_{b} = 5,0\,kg}$, suspenso de uma viga por um cabo de comprimento $\color{Sepia}{l = 2,0\,m}$. Um projétil é de $\color{Sepia}{m_{p}= 25,0\,g}$ é disparado de curta distância na direção horizontal passando pelo centro de gravidade do bloco, penetrando até próximo do mesmo. Com a energia do impacto, o pêndulo oscila e sobe até uma altura $h$ acima da posição de equilíbrio. Quanto ao comportamento do sistema em relação a energia e momento linear podemos afirmar:
( )a) a energia potencial gravitacional do sistema no ponto de elevação máxima é igual à energia cinética do projétil no momento do disparo;
( )b) a energia potencial gravitacional do sistema no ponto de elevação máxima é igual à energia cinética do sistema imediatamente após o impacto do projétil;
( )c) o momento linear do sistema é constante, mesmo no ponto de elevação máxima;
( )d) a energia cinética perdida é transformada em energia potencial armazenada no interior do bloco;
( )e) N.d.a.
10. Um vagão ferroviário se movimenta sobre um trecho de linha reta, sem atrito, com velocidade $v_{1}$, quando se choca com outros dois vagões parados no trilho. O sistema de engates encaixa e, supondo que as massas dos três vagões é igual, determine a velocidade do conjunto logo após o choque, em função da velocidade do primeiro.
( )a) $v_{f} = 3\times v_{1}$;
( )b) $v_{f} = \frac{v_{1}}{3}$;
( )c) $v_{f} = \sqrt{3}\times v_{1}$;
( )d) $v_{f} = 3^{2}\times v_{1}$;
( )e) $v_{f} = \sqrt{3\times v_{1}}$.
11. Uma bola de bocha de massa $\color{Sepia}{m = 1\,kg}$, com velocidade $\color{Sepia}{v_{1} = 1,5\,m/s}$, atinge outra bola de mesma massa posicionada na cancha de jogo, num ponto que faz essa bola sair numa direção que forma um ângulo de $\color{Sepia}{\theta = 30^{0}}$ com a direção inicial da primeira. Admitindo ser um choque perfeitamente elástico, qual é a direção da velocidade final da primeira bola, em relação à sua direção inicial?
( )a) $\gamma = 45^{0}$;
( )b) $\gamma = 30^{0}$;
( )c) $\gamma = 60^{0}$;
( )d) $\gamma = 90^{0}$;
( )e) $\gamma = 25^{0}$.
12. Duas bolas de bilhar se movimentam sobre a mesa, seguindo na mesma direção e sentido. A primeira com velocidade $\color{Sepia}{v_{i1} = 0,30\,m/s}$ e a segunda com velocidade $\color{Sepia}{v_{i2} = 0,50\,m/s. Supondo a colisão parcialmente elástica e seu coeficiente de restituição valendo $\color{Sepia}{e = 0,85}$, as velocidades imediatamente após a colisão serão:
( )a) $v_{f1} = 0,485\,m/s; v_{f2} = 0,315\,m/s$;
( )b) $v_{f1} = 0,50\,m/s; v_{f2} = 0,30\,m/s$;
( )c) $v_{f1} = 0,35\,m/s; v_{f2} = 0,45\,m/s$;
( )d) $v_{f1} = 0,25\,m/s; v_{f2} = 0,55\,m/s$;
( )e) $v_{f1} = 0,40\,m/s; v_{f2} = 0,60\,m/s$.
13. Uma bola de borracha maciça cai de uma altura $\color{Sepia}{h}$ e se choca com o piso liso e horizontal. Se o coeficiente de restituição entre a bola e o piso é igual a $\color{Sepia}{e = 0,92}$, qual é a altura que a bola atinge na primeira vez?
( )a) $h’ \simeq0,80\times h$;
( )b) $h’ \simeq 0,90\times h$;
( )c) $h’ \simeq 0,75\times h$;
( )d) $h’ \simeq 0,85\times h$;
( )e $h’ \simeq 1,84\times h$.
14. Uma bola de borracha maciça é lançada para cima, com velocidade inicial de $\color{Sepia}{v_{0} = 20,0\,m/s}$, num lugar em que a aceleração da gravidade é igual a $\color{Sepia}{g = 10,0\,m/s^{2}}$ a uma altura $\color{Sepia}{h_{0} = 10\,m}$ . Sendo o coeficiente de restituição da bola ao se chocar com o solo $\color{Sepia}{e = 0,90}$, a que altura a bola irá rebater no primeiro impacto com o chão?
( )a) 27,0 m;
( )b) 23,5 m;
( )c) 24,3 m;
( )d) 26,2 m;
( )e) 25,0 m.
15. Uma mola de constante elástica $\color{Sepia}{k = 800,0\,N/m}$ está disposta sobre um plano horizontal, alinhada com o movimento de dois carrinhos que se movem um ao encontro do outro. O primeiro tem massa de $\color{Sepia}{m_{1} = 30,0\,kg}$ e velocidade de $\color{Sepia}{v_{i1} = 10,0\,m/s}$ e o outro tem velocidade $\color{Sepia}{v_{i2}=15,0\,m/s}$ e sua massa é de $\color{Sepia}{m_{2} = 40,0\,kg}$. Eles atingem as extremidades da mola ao mesmo tempo, comprimindo-a. Logo após, a mola se distende, devolvendo as energias aos dois carrinhos. Podemos raciocinar como se tratando de um choque perfeitamente elástico. Qual será a velocidade de ambos após deixarem o contato com a mola?
( )a) $v_{f1} = 16,0\,m/s; v_{f2} = 12,0\,m/s$;
( )b) $v_{f1} = 15,0\,m/s; v_{f2} = 10,0\,m/s$;
( )c) $v_{f1} = 18,57\,m/s; v_{f2} = 6,43\,m/s$;
( )d) $v_{f1} = 13,0\,m/s; v_{f2} = 17,0\,m/s$;
( )e) $v_{f1} = 10,0\,m/s; v_{f2} = 15,0\,m/s$.
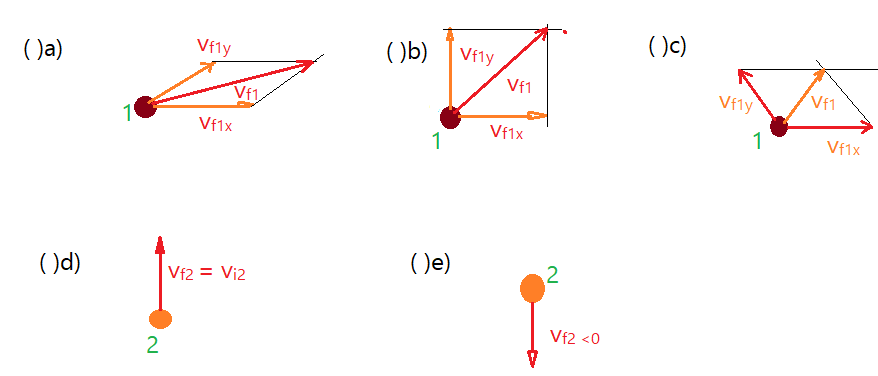
16. Duas bolas de bilhar estão em movimento sobre a mesa de jogo. Elas tem massas iguais e a primeira possui velocidade $\color{Sepia}{v_{i1} = 0,10\,m/s}$. A segunda tem velocidade de $\color{Sepia}{v_{i2}=0,20\,m/s}$, como mostra a figura abaixo.
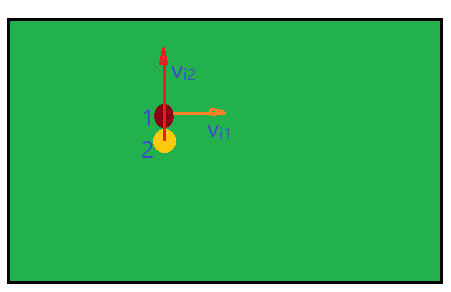
Assinale a figura a seguir que representa melhor o efeito da colisão entre as duas bolas.
Se tiver alguma dúvida, peça ajuda por meio de um dos canais listados abaixo. Não guarde as dúvidas para depois. Boa aprendizagem.
Curitiba, 05 de setembro de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
