FI.ME.018-02-Física – Mecânica – Hidráulica – Hidrodinâmica (II)
Aplicações do Teorema de Bernoulli
Daniel Bernoulli, nascido na Suíça em 08/02/1700, membro de uma dinastia de matemáticos suíços. Faleceu em 17/03/1782, deixou, entre outros tantos legados, como vimos um Teorema que traduzimos em uma equação fundamental no estudo dos fluidos em movimento.
Medidor de Venturi ou Tubo de Venturi
Giovanni Batista Venturi, viveu de 1746 a 1822. Foi o criador de um método de medir a velocidade de escoamento de fluidos. Consiste em um tubo de secção transversal de área $S_{1}$. Em certo ponto está colocado um funil seguido de um estreitamento onde temos $S_{2}$ e ali o fluido escoa com velocidade maior, para depois retornar ao original. O aumento de velocidade é devido à compressão das “linhas de corrente” , uma vez que a vazão se conserva. Um manômetro de líquido (geralmente mercúrio) é inserido com uma extremidade no estreitamento e com a outra na região da secção 1. A diferença das velocidades de escoamento, provoca uma diferença de pressão que é avaliada pelo manômetro. Veja a figura a seguir.
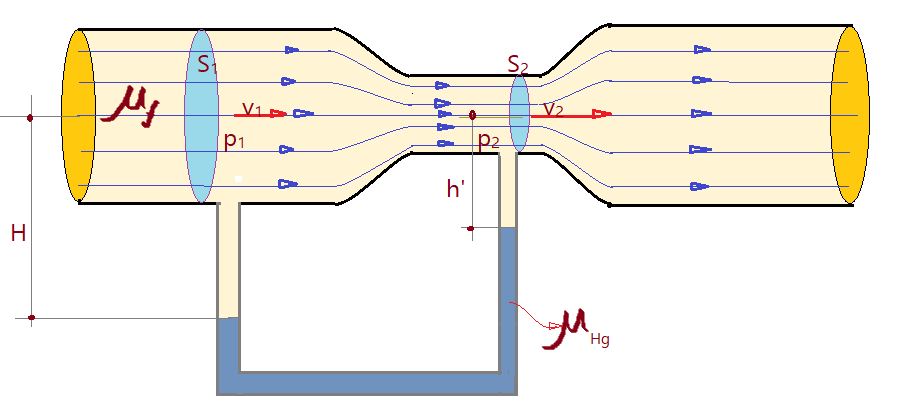
Sendo o conjunto todo posto na horizontal, podemos dizer que as alturas dos dois pontos no centro do duto, nas secções retas $S_{1}$ e $S_{2}$, são iguais e a equação do Teorema de Bernoulli fica assim:
$$\color{Maroon}{p_{1} + \frac{\mu_{f}}{2}\times {{v}_{1}}^{2} = p_{2} + \frac{\mu_{f}}{2}\times{v_{2}}^{2}}$$
Dela tiramos:
(I) $$\color{Sepia}{p_{1} – p_{2} = \frac{\mu_{f}}{2}\times[{v_{2}}^{2} -{v_{1}}^{2}]}$$
Da equação da continuidade tiramos:
$$\color{Maroon}{S_{1}\times {v_{1}} = S_{2}\times{v_{2}}}$$
(II) $$\color{Sepia}{v_{2} = \frac{S_{1}}{S_{2}}\times {v_{1}}}$$
Substituindo (II) em (I):
$p_{1} – p_{2} = \frac{\mu_{f}}{2}\times\left[\left(\frac{S_{1}}{S_{2}}\times{{v}_{1}}\right)^{2} – {{v}_{1}}^{2}\right]$$\Leftrightarrow$$p_{1} – p_{2} =\frac{\mu_{f}}{2}\times\left[\frac{S_{1}^2}{S_{2}^2}\times v_{1}^{2} – v_{1}^{2}\right]$
$p_{1} – p_{2} = \frac{\mu_{f}\times v_{1}^{2}}{2}\times\left[\left(\frac{S_{1}^{2}}{S_{2}^{2}}\right) -1\right]$
(III) $$\color{Sepia}{p_{1} – p_{2} = \left(\frac{\mu_{f}}{2}\right)\times v_{1}^{2}\left(\frac{S_{1}^{2} – S_{2}^{2}}{S_{2}^{2}}\right)}$$
Do manômetro, podemos tirar, aplicando o princípio de Stevin relativo ao equilíbrio dos fluidos em vasos comunicantes.
$p_{1} + \mu_{f} g H = p_{2} + \mu_{f} g (H-h) + \mu_{Hg} g h$
$p_{1} – p_{2} = \mu_{f} g H – \mu_{f} g h + \mu_{Hg} g h – \mu_{f} g H$
Cancelando os termos simétricos, ficamos com:
(IV) $$\color{Sepia}{p_{1} – p_{2} = gh(\mu_{Hg} – \mu_{f})}$$
Podemos igualar as equações (III) e (IV).
$\left(\frac{\mu_{f}}{2}\right)\times v_{1}^{2}\left(\frac{S_{1}^{2} – S_{2}^{2}}{S_{2}^{2}}\right) = gh(\mu_{Hg} – \mu_{f})$
$\frac{\mu_{f} v_{1}^{2}}{2\times S_{2}^{2}} = gh(\mu_{Hg } – \mu_{f})$
$v_{1}^{2} = \frac{2 S_{2}^{2} g h(\mu_{Hg} – \mu_{f})}{\mu_{f}(S_{1}^{2} – S_{2}^{2})}$$\Leftrightarrow$$\sqrt{v_{1}^{2}} = \sqrt{\frac{2 S_{2}^{2} g h(\mu_{Hg} – \mu_{f})}{\mu_{f}(S_{1}^{2} – S_{2}^{2})}}$
$$\color{Navy}{v_{1} = S_{2}\sqrt{\frac{2 g h(\mu_{Hg} – \mu_{f})}{\mu_{f}(S_{1}^{2} – S_{2}^{2})}}}$$
Tubo de Pitot ou Medidor de Pitot
Henri Pitot em 1732, apoiado no Teorema de Bernoulli criou um dispositivo para medir a velocidade de escoamento de um gás, como por exemplo o ar. Consiste em um tubo, envolto em uma cavidade envolvente, provida de aberturas pequenas e simetricamente dispostas nas paredes, em direção normal ao tubo. O tubo e a cavidade estão ligadas às aberturas de ambos os ramos de um manômetro em forma de U, com um líquido barométrico, geralmente mercúrio, como mostra a figura.
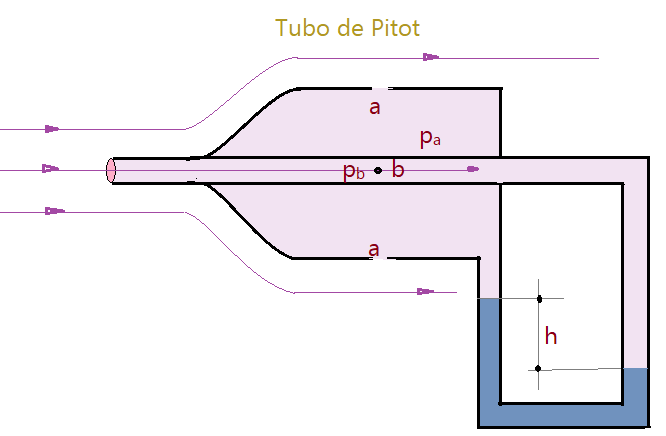
O gás que flui para dentro do tubo atinge velocidade nula no ponto $b$, que se situa suficientemente distante do final do tubo para isso. As linhas de corrente que circundam o conjunto, ficam comprimidas na região próxima, de modo a provocar um aumento de velocidade. Em consequência, nas proximidades das aberturas $a$ teremos uma pressão menor $p_{a}$, que se transmite ao interior da cavidade, provocando uma elevação do líquido manométrico no ramo esquerdo do tubo em forma de U.
Como a velocidade no ponto $b$ é nula, no ramo direito do tubo temos a pressão normal do gás em movimento $p_{b}$. Esta pressão é maior do que no outro ramo $p_{b} \lt p_{a}$. Como $v_{b} = 0$, na equação do Teorema de Bernoulli teremos:
(I) $$\color{Maroon}{p_{a} + \frac{\mu_{gas}}{2}\times v^{2} = p_{b}}$$
A deflexão no manômetro nos permite escrever:
(II) $$\color{Maroon}{p_{a} + \mu_{Hg} g h = p_{b}}$$
Estabelecendo a igualdade entre (I) e (II):
$p_{a} + \frac{\mu_{gas}}{2}\times v^{2} = p_{a} + \mu_{Hg} g h$
Cancelamos os termos simétricos e teremos:
$v^{2} = \frac{2gh\mu_{Hg}}{\mu_{gás}}$$\Leftrightarrow$$\sqrt{v^{2}} = \sqrt{\frac{2\mu_{Hg}gh}{\mu_{gás}}}$
$$\color{Navy}{v = \sqrt{\frac{2\mu_{Hg}gh}{\mu_{gás}}}}$$
Bomba de spray
Em todas as casas, pelo menos na maioria delas, existe um ou vários exemplares desse tipo de equipamento. Há maiores, menores e diferentes formas. Há os que são acionados por uma alavanca que comprime um pistão, produzindo o fluxo de ar e outras como mostra a figura, tem um balão, habitualmente de borracha para produzir o mesmo efeito. Um fino tubo está imerso no líquido dentro do recipiente e a extremidade superior está em contato com a canalização de ar. O jato de ar, a alta velocidade, produz uma deflexão do líquido por causa da queda de pressão no local e o líquido sobe. A superfície livre do líquido está sob ação da pressão atmosférica por meio de um furo finíssimo por onde o ar entra.
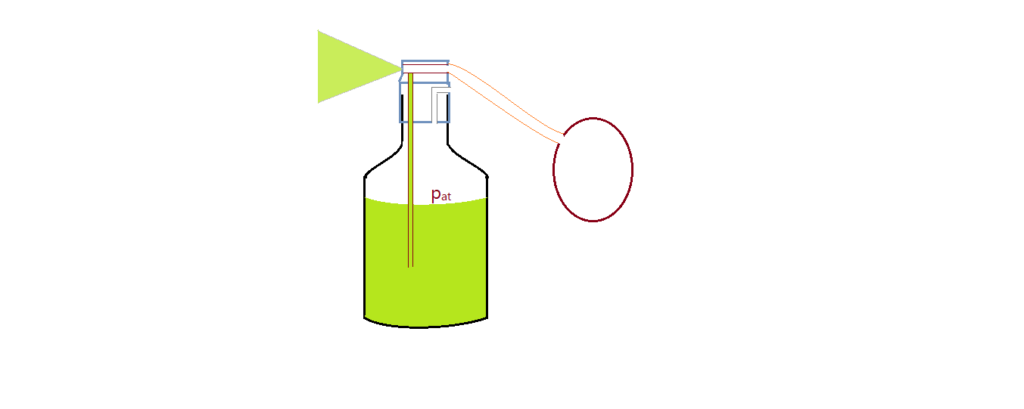
Em contato com o ar ele se fragmenta em gotículas formando um jato de spray. É usado para borrifar perfumes, desinfetantes, inseticidas ou qualquer líquido que se queira espargir.
Empuxo dinâmico em asas e aerofólios
Se olharmos no começo desse texto, veremos o escoamento laminar e turbulento. Esse mesmo fato ocorre nas asas de aviões e nos aerofólios de veículos, para produzir determinados efeitos baseados na variação de pressão obtida com isso.
Uma asa de avião é plana na parte inferior e mais alta na parte frontal, afilando até a junção das duas linhas onde terminam os “flaps”, que são dispositivos de manobras para subir ou descer de nível. Dessa maneira o fluxo de ar, com o avião ou veículo em movimento, fica mais veloz na parte superior do que na inferior. Assim teremos um gradiente de pressão entre dois pontos situados acima e abaixo da asa. Olhemos a figura.
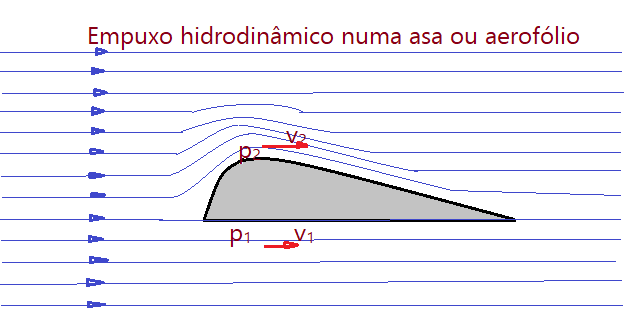
Pela equação do Teorema de Bernoulli:
$$\color{Maroon}{p + \frac{\mu}{2}\times v^{2} = k}$$
Para dois pontos $p_{1}$ e $p_{2}$, situados abaixo e acima da asa:
$p_{1} + \frac{\mu}{2}\times v_{1}^{2} = p_{2} + \frac{\mu}{2}\times v_{2}^{2}$
$p_{2} = p_{1} + \frac{\mu}{2}\times v_{1}^{2} – \frac{\mu}{2}\times v_{2}^{2}$$\Leftrightarrow$$p_{2} = p_{1} + \frac{\mu}{2}\times (v_{1}^{2} – v_{2}^{2})$
$$\color{Navy}{p_{2} = p_{1} + \frac{\mu}{2}\times(v_{1}^{2} – v_{2}^{2})}$$
Podemos com isso determinar a força de empuxo que atua sobre uma asa ou aerofólio, que pode ser “para cima” ou “para baixo”, o falado “downforce” nos automóveis de corrida.
$$\color{Navy}{F = S\times{(p_{1} – p_{2})}}$$
Empuxo sobre uma bola em movimento
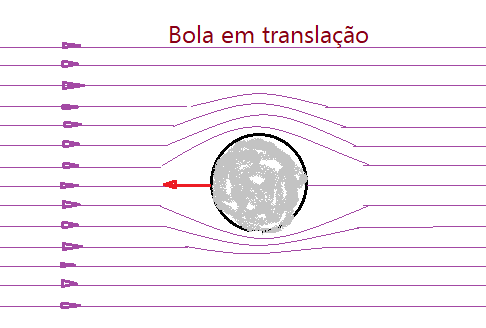
1)Bola em translação – a bola somente em translação apenas desloca as linhas de corrente do ar para os lados e passa. Seu movimento fica sujeito basicamente a um impulso inicial e a ação gravitacional. Observe a figura.
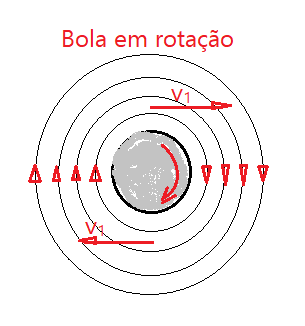
2)Bola em rotação – a bola produz um efeito de rotação sobre o ar que está ao seu redor. Este efeito se atenua na medida em que aumenta a distância, quando a energia se dissipa. Veja a figura que ilustra um pouco a situação.
3)Bola em rotação e translação – nessa situação ocorrem os famosos movimentos “em curva” que se observa nas cobranças de faltas no futebol, no tênis, tênis de mesa, voleibol e outros esportes praticados com uso de bolas.
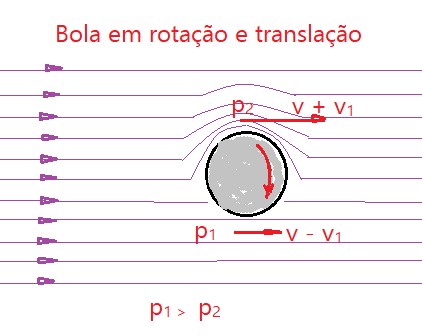
Existem diferentes efeitos conseguidos com formas diferentes de bater na bola, seja com o pé, a mão, um taco ou raquete. Os especialistas fazem jogadas que parecem mirabolantes, até mesmo impossíveis.
Empuxo dinâmico em velas de barcos
Certamente já assistiu a uma prova de barcos à vela ou filmes de navios veleiros, onde ocorre o que se costuma chamar de “navegar contra” o vento.
Cabe aí perguntar: “Como é possível navegar contra o vento, usando a força dele?”
Basta lembrar que geralmente os grandes barcos possuem mais de uma vela, entre elas as duas principais são a mestra e a bujarrona. Observemos o desenho que tenta reproduzir como isso pode ser feito.
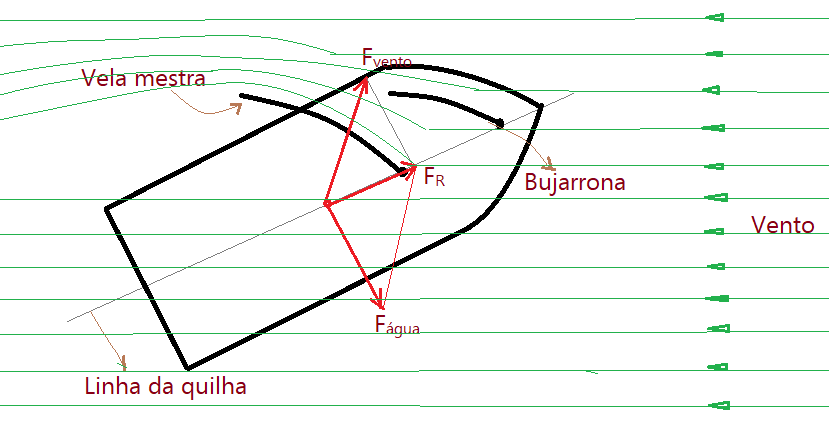
As duas velas reproduzem o efeito de uma asa ou aerofólio. O resultado é uma força $F_{vento}$, numa direção inclinada em relação à linha da quilha e próxima da normal à vela. Por baixo do barco temos a “bolina”, que funciona na água de modo semelhante à vela e resulta em uma força $F_{água}$ próxima da perpendicular a linha da quilha. A resultante dessas duas forças impulsiona o barco para frente, aparentemente contra o vento, por mais que isso possa parecer paradoxal.
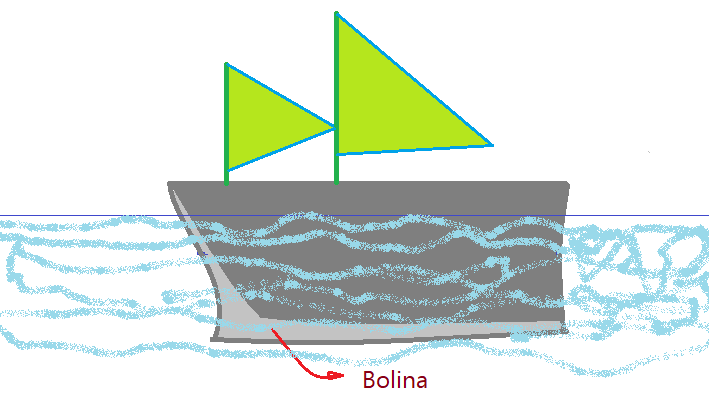
Na parte final da bolina existe o leme que é móvel e permite controlar a direção em que o navio vai se deslocar. É comandado por uma roda, existente no castelo de proa e quem o manipula é o piloto ou mesmo o comandante da embarcação.
Vamos exercitar
01. Um conduto e constituído por 2 trechos, com diâmetros de $D_{A}=0,25\,m$ e $D_{B}=0,20\,m$, como mostra a figura abaixo. Sabendo-se que a pressão no ponto A é de $p_{A}=1,5\,Kgf/cm^{2}$ e que a velocidade no trecho de maior diâmetro é de $V_{A}=0,6\,m/s$, calcule a vazão no conduto, a velocidade de escoamento em B e a pressão nesse ponto. (Supor movimento sem atrito).
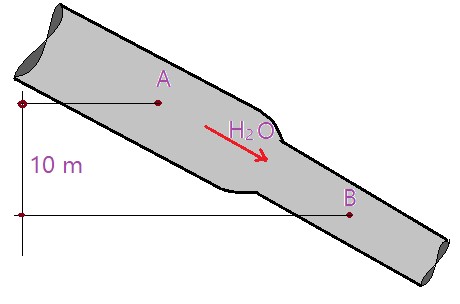
Dados: $h_{A}=10,0\,m$, $p_{A}=1,5\,kgf/cm^{2}=147000\,N/m^{2}$, $D_{A}=0,25\,m$, $D_{B}=0,20\,m$, $v_{A}=0,6\,m/s$.
A vazão em A:
$\phi_{A}= S_{A}\times v_{A}$$\Leftrightarrow$$\phi = \frac{\pi\times{D_{A}}^{2}}{4}$
$\phi = \frac{\pi\times{0,25}^{2}}{4}$$\Leftrightarrow$$\phi=0,029\,m^{3}/s$
$$\color{Navy}{\phi = 29,5\,l/s}$$
Como o escoamento é uniforme, o fluxo em B é igual ao de A. Podemos então calcular a velocidade pela equação da continuidade.
$$\color{Maroon}{\phi_{A} = \phi_{B}}$$
$S_{A}\times v_{A} = S_{B}\times v_{B}$$\Leftrightarrow$$0,029 = \frac{\pi\times{0,20}^{2}}{4}\times v_{B}$
$v_{B} = \frac{0,0295\times 4}{\pi\times{0,20}^{2}}$$\Leftrightarrow$$v_{B} = 0,939\,m/s$
A pressão no ponto B, é determinada pela equação do Teorema de Bernoulli.
$$\color{Maroon}{p_{A}+\mu_{H_{2}O}\times g h_{A}+ \frac{\mu_{H_{2}O}\times v_{A}^{2}}{2} = p_{B}+\mu_{H_{2}O}\times g h_{B} +\frac{\mu_{H_{2}O}\times v_{B}^{2}}{2}}$$
$p_{B}= p_{A}+\mu_{H_{2}O}\times g h_{A}+ \frac{\mu_{H_{2}O}\times v_{A}^{2}}{2} – \mu_{H_{2}O}\times g h_{B} +\frac{\mu_{H_{2}O}\times v_{B}^{2}}{2}$
O termo que contém $h_{B}$ por conta da nulidade desse fator pode ser cancelado, pois o resultado seria também zero.
$p_{B}= 1,47\times 10^{5} + 10^{3}\times 10\times 10+\frac{{10}^{3}\times{0,6}^{2}}{2} – \frac{{10}^{3}\times{0,939}^{2}}{2}$
$p_{B}=1,47\times 10^{5} +1,0\times 10^{5} + 0,18\times {10}^{3} – 0,441\times {10}^{3}$$\Leftrightarrow$$p_{B} = 2,47\times 10^{5} – 0,00261 \times {10}{5}$
$p_{B} = 2,4674\times 10^{5}\,N/m^{2}$
Sendo $1\,kgf = 9,8\,N$ e $1\,m^2 = 10^{4}\,cm^2$
$p_{B}=\frac{2,4674}{9,8}\frac{kgf}{10^{4}cm^{2}}$
$$\color{Navy}{p_{B} = 2,52\,kgf/cm^{2}}$$
02. Uma tubulação horizontal transporta $\phi=850\,L/s$ de água. Em A tem ela o diâmetro de $D_{A}=450\,mm$ e a pressão de $p_{A}=0,700\,kgf/cm^{2}$; em B, o seu diâmetro é de $D_{B}=900\, mm$ e a pressão de $p_{B}=0,763\,kgf/cm^{2}$. Calcular as velocidades nos dois pontos A e B.
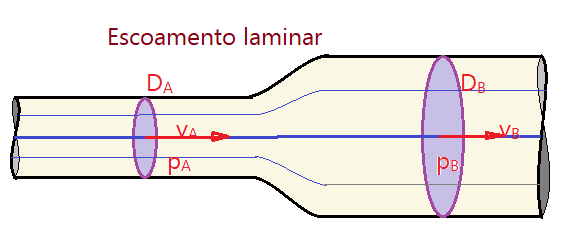
Dados:
$\phi = 850\,L/s=0,85\,m^{3}/s$, $D_{A}=450\,mm$, $D_{B}=900\,mm$, $p_{A}=0,700\,kgf/cm^{2}$ e $p_{B}=0,763\,kgf/cm^2$
A equação do fluxo, nos permite determinar as velocidades nos pontos A e B.
$$\color{Maroon}{\phi = S_{A}\times v_{A} = S_{B}\times v_{B}}$$
$0,850 = \frac{\pi\times {(0,45)}^{2}}{4}\times v_{A}$$\Leftrightarrow$$v_{A}=\frac{0,850\times 4}{0,2025\times{3,14}}$
$\color{Navy}{v_{A}=\frac{3,400}{0,636}= 5,346\,m/s}$$
$0,850=\frac{\pi\times{(0,90)}^{2}}{4}\times v_{B}$$\Leftrightarrow$$v_{B}=\frac{0,850\times 4}{0,81\times{3,14}}$
$v_{B}=\frac{3,400}{2,5434}= 1,337\,m/s$
$$\color{Navy}{v_{B}=1,337\,m/s}$$
03. A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto $S$ do sifão deve ser maior que $p_{s}\gt – 60 kPa$ em pressão relativa e desprezando as perdas de carga determine a velocidade da água $\mu_{H_{2}O}=10^{3}\,kg/m^{3}$ no sifão e a máxima altura que o ponto $S$ pode ter em relação ao ponto A.
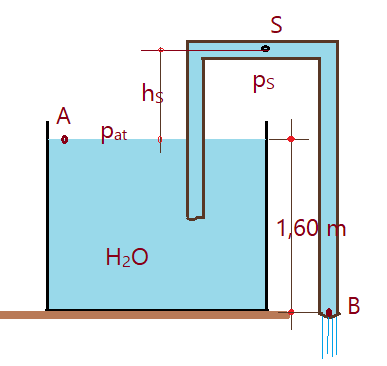
Para determinar a velocidade de escoamento da água pelo tubo do sifão no ponto B, usaremos a equação do Teorema de Bernoulli.
A velocidade de descida em A é muito pequena e podemos desconsiderá-la, ou seja, supor igual a zero. A pressão atmosférica nos pontos A e B é a mesma.
$p_{A} + \mu_{H_{2}O} g h_{A} + \frac{\mu_{H_{2}O}}{2}\times{ v_{A}}^{2} = p_{B} + \mu_{H_{2}O} gh + \frac{\mu_{H_{2}O}}{2}\times {v_{B}}^{2}$
Cancelando os termos nulos e os fatores comuns, teremos:
$gh_{A} = gh){B} + \frac{v_{2}}{2}$$\Leftrightarrow$$g(h_{A} – h_{B}) = \frac{v_{B}^{2}}{2}$
$v_{B}^{2} = 2 g\Delta h$$\Leftrightarrow$$\sqrt{v_{B}^{2}}=\sqrt{2g\Delta h}$
$v_{B} = \sqrt{2\times 10\times 1,6}$$\Leftrightarrow$$v_{B} = 5,66$
$$\color{Navy}{v_{B}=5,66\,m/s}$$
Para determinar a altura máxima que poderá ter o ponto $S$ em relação ao ponto $A$, usaremos a equação de Bernoulli, igualando o segundo membro à zero, pois a pressão no ponto $S$ é relativa ou manométrica.
$0 = p_{S} + \mu_{H_{2}O} g h_{S} + \mu_{H_{2}O}\frac{v_{B}^{2}}{2}$$\Leftrightarrow$$ 0 = -60\times{10}^{3} + {10}^{3}\times{10}\times h_{S} + {10}^{3}\frac{{5,66}^{2}}{2}$
${10}^{4}\times h_{S} = 60\times{10}^{3} – 16,018\times{10}^{3}$$\Leftrightarrow$$h_{S}=\frac{{(60-16,018)}\times{10}^{3}}{{10}^{4}} = 4,398\,m$
$$\color{Navy}{h_{S} = 4,398\,m}$$
O ponto $S$ pode estar no máximo a uma altura de $4,398\,m$.
04. Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:
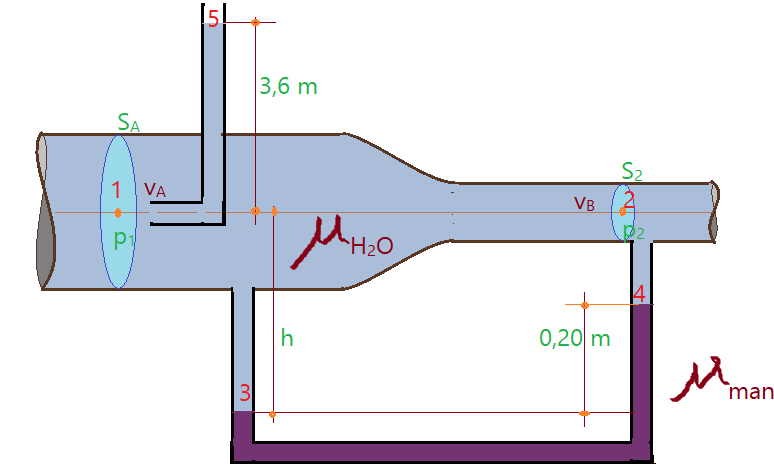
- $\mu_{água}= 10^{3}\,kg/m^{3}$;
- $\mu_{man} = 7\times{10}^{3}\,kg/m^{3}$;
- $S_{A}= 400\, cm^{2}$;
- $p_{2}= 20 kPa$;
- $g= 10\,m/s^{2}$.
Vamos estudar a pressão nos pontos $1$ e $5$, aplicando a equação de Bernoulli.
$p_{1} + \mu_{H_{2}O}\times g\times y + \frac{\mu_{H_{2}O}\times v_{A}^{2}}{2} = p_{5} + \mu_{H_{2}O}\times g\times h_{5} + \frac{\mu_{H_{2}O}\times v_{5}}{2}$
A velocidade no ponto $5$ é nula e a pressão é apenas a atmosférica. Como estamos trabalhando com a pressão manométrica, da equação acima resta:
$p_{1} + \frac{v_{A}^{2}}{2}\times \mu_{H_{2}O} = \mu_{H_{2}O}\times g\times h_{5}$$\Leftrightarrow$$p_{1} + \frac{v_{A}^2}{2}\times\mu_{H_{2}O} = 10^{3}\times 10\times {3,6}$
$p_{1} + \frac{v_{A}^2}{2}\times\mu_{H_{2}O} = 36\times 10^{3}$
Para concluirmos a solução falta-nos o valor da pressão $p_{1}$. Vamos então analisar o manômetro que existe abaixo dos pontos $1$ e $2$.
Aplicaremos o princípio de Stevin. A diferença de pressão entre os pontos será dada pela coluna líquida nos dois ramos do manômetro.
$p_{1} + \mu_{H_{2}O}\times g\times h = p_{2} + \mu_{H_{2}O}\times g\times {(h – 0,20)} + \mu_{man}\times g\times 0,20$$p_{2} – p_{1} = \mu_{H_{2}O}\times g\times h – \mu_{H_{2}O}\times g\times {(h – 0,20)} – \mu_{man}\times g\times 0,20$
$p_{2} – p_{1} = \mu_{H_{2}O}\times g\times h – \mu_{H_{2}O}\times g\times h + \mu_{H_{2}O}\times g\times {0,20} – \mu_{man}\times g\times 0,20$$
$p_{2} – p_{1} = -0,20\times 10\times{(\mu_{man} – \mu_{H_{2}O})}$$\Leftrightarrow$$20\times{10}^{2} – p_{1} =-2,0\times{7\times{10}^{3} – {10}^{3}}$
$p-{1} = 20\times {10}^{3} + 12\times{10}^{3}$$p_{1} = 32\times{10}^{3}$
$$\color{Maroon}{p_{1}= 32\times{10}^{3}\,Pa}$$
Podemos agora determinar a velocidade no ponto A, voltando à equação que obtivemos acima.
$p_{1} + \frac{{v_{A}}^{2}}{2}\times \mu_{H_{2}O} = 36\times{10}^{3}$$\Leftrightarrow$$\frac{v_{A}^{2}}{2} = 36\times{10}^{3} – 32\times{10}^{3}$
${v_{A}}^{2}\times{10}^{3} = 2\times 4\times{10}^{3}$$\Leftrightarrow$$\sqrt{v_{A}^{2}} = \sqrt{2\times 4}$
$$\color{Maroon}{v_{A} = 2,83\,m/s}$$
Agora temos as informações para calcular o fluxo de escoamento da água.
$$\color{Sepia}{\phi = S_{A}\times v_{A}}$$
$\phi = 0,04\times 2,83 = 0,1132\,m^{3}/s$
$$\color{Navy}{\phi = 113,2\,l/s}$$
05. De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de $1,0\,m_{H_{2}O}$. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na figura abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:
- Perdas de carga linear na tubulação: $0,08\,m/m$;
- Perda de carga concentrada por joelho $90^{0} =0,5\, m/peça$;
- Perda de carga concentrada por Tê de saída lateral: $2,0 m/peça$;
- Perda de carga concentrada por registro de gaveta: $1,2 m/peça$;
- Despreze as cargas cinéticas.
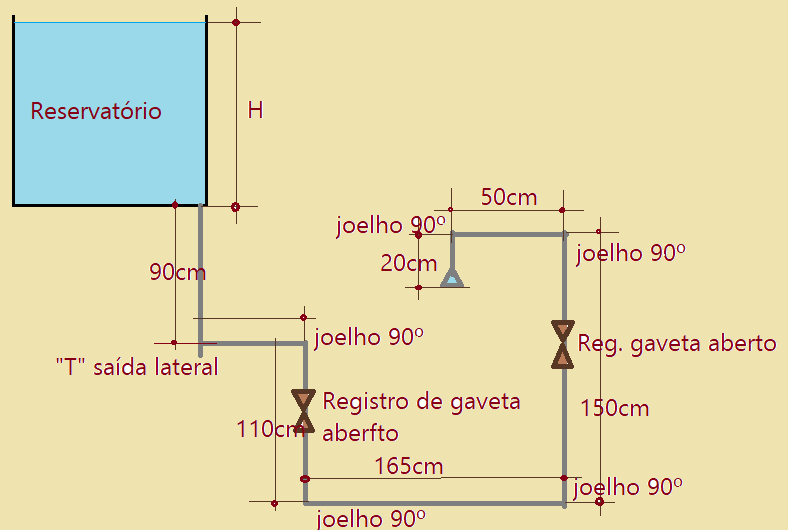
Resolução:
Iremos aplicar a equação de Bernoulli entre a superfície livre do reservatório e a saída de chuveiro. Como existem perdas de carga elas devem ser consideradas e levadas em conta no cômputo final. Sendo desconsideradas as cargas cinéticas, restam apenas as pressões devidas às alturas de coluna d’água. O que resulta em:
$H + 0,90 + 1,10 = 1,50 – 0,20 + 1,0 +\Delta H$
$H = 2,50 – 2,0 – 0,20+ \Delta H$$\Leftrightarrow$$H = 0,30 +\Delta H$
Vamos calcular as perdas de carga pela extensão da tubulação e pelos pontos de perda.
$L = 0,90 + 0,35 + 1,10 + 1,65 + 1,50 + 0,50 + 0,20 = 6,20\,m$
$\Delta H_{d} = 6,20\times 0,08 = 0,496\,m$
Temos dois registros de gaveta: $L_{R}= 2\times 1,2 = 2,40\,m$
Cinco joelhos de $90^{0}$$\rightarrow$$L_{j}=5\times 0,50 = 2,50\,m$
Um “T”com saída lateral: $L_{T}=1\times 2,0\,m$
A soma dos comprimentos equivalentes dos pontos de perda é:
$L_{p}= 2,40 + 2,50 + 2,00 = 6,90\,m$
Assim as perdas de carga nos pontos é:
$\Delta H_{p}= 6,90\times 0,08 = 0,552\,m$
$\Delta H_{t}= \Delta H_{d} + \Delta H_{p}$
$\Delta H_{t} = 0,496 + 0,552 = 1,048\,m$
Substituindo na expressão que resultou ao aplicarmos a equação de Bernoulli:
$$H = 0,3 + 0,496 + 0,552 = 1,348\,m$$
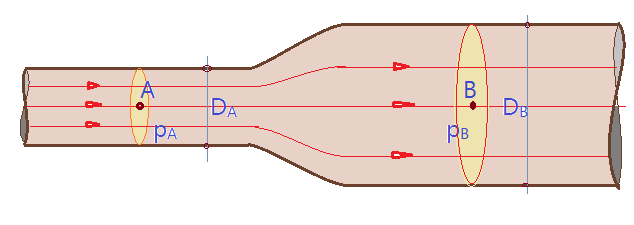
06. Uma tubulação horizontal transporta $\phi= 850\, l/s$ de água. Em A ela tem diâmetro de $D_{A} =450\,mm$ e a pressão de $p_{A} =0,700\,Kgf/cm^{2}$ em B, o diâmetro é de $D_{B}=900\, mm$ e a pressão de $P_{B} = 0,763\, Kgf/cm^{2}$. Calcular a perda de carga entre os dois pontos.
Dados:$\phi = 850\,l/s =0,850\,m^{3}/s$, $D_{A} = 450\,mm= 0,45\,m$, $D_{B} = 900\,mm=0,90\,m$, $p_{A} =0,700\,kgf/cm^{3}=68,6\times{10}^{3}\,N?m^{3}$ e $p_{B} = 0,763\,kgf/cm^{2}=74,774\times{10}^{3}\,N/m^{3}$
Se o fluxo é de $0,850 m^{3}/s$, podemos determinar as velocidades de escoamento em A e B.
$$\color{Maroon}{\phi = S\times v}$$
$v = \frac{\phi}{S}$$\Leftrightarrow$$V_{A} = \frac{\phi}{\frac{\pi\times D_{A}^{2}}{4}}$
$v_{A} = \frac{\phi\times 4}{\pi\times {D_{A}}^{2}}$$\Leftrightarrow$$v_{A}= \frac{0,85\times 4}{\pi\times {0,45}^{2}}$
$$\color{Sepia}{v_{A}= \frac{3,4}{0,636}=5,346\,m/s}$$
$v_{A} = \frac{\phi\times 4}{\pi\times {D_{A}}^{2}}$$\Leftrightarrow$$v_{B} = \frac{0,85\times 4}{\pi\times {D_{B}}^{2}}$
$$\color{Sepia}{v_{B} = \frac{3,4}{2,545} = 1,336\,m/s}$$
Calculando a perda de carga, pela equação de Bernoulli. Sendo tubo horizontal, as alturas do eixo de fluxo é a mesma e o termo da carga potencial se anula.
$p_{A} + \frac{\mu_{água}\times {v_{A}^{2}}}{2} = p_{B} + \frac{\mu_{água}\times {v_{B}^{2}}}{2} + \Delta H$
$68600 + \frac{{10}^{3}\times {(5,346)}^{2}}{2} = 74774 + \frac{{10}^{3}\times{(1,336)}^{2}}{2} +\Delta H$$\Leftrightarrow$$ 68600 + 14290 = 74774 + 892,45 +\Delta H$
$\Delta H = 82890 – 75666,45$$\Leftrightarrow$$\Delta H=7223,55\,Pa$
$$\color{Navy}{\Delta H = 7223,55\,Pa}$$
Convertendo para a unidade $m.c.a$, teremos:
$101325\times x = {7223,55}\times {10,33}$$\Leftrightarrow$$x – \frac{74619,2715}{101325} = 0,736\, m.c.a.$
$$\color{Orchid}{\Delta H = 0,736\,m.c.a}$$
07. Um tubo de $D_{1}=300\,mm$ está ligado por meio de uma redução, a outro de $D_{2}=100\,mm$, como mostra a figura abaixo. 0s pontos 1 e 2 acham-se à mesma altura, sendo a pressão em 1 de $p_{1}=2,1\,kgf/cm^{2}$ , $Q = 28,3\,l/s$ e $\Delta p = 0,21\, kgf/cm^{2}$ perda de energia entre 1 e 2. Calcular a pressão para:
a) água;
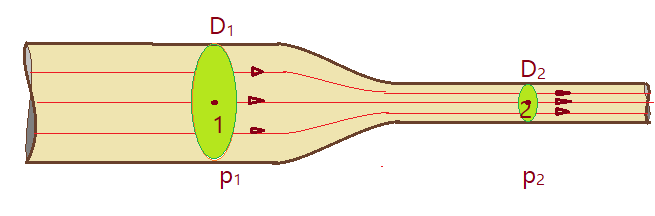
b) óleo (d = 0,80).
Dados:$D_{1}=0,30\,m$, $D_{2}=0,10\,m$, $p_{1}=2,1\,kgf/cm^{2}=20,58\times{10}^{4}\,Pa$, $\Delta p =2,058\times{10}^{4}\,Pa$ e $\phi = 0,0283\,m^{3}/s$.
Começaremos por calcular as velocidades nos pontos 1 e 2.
$$\color{Maroon}{\phi = S\times v}$$
$v_{1}=\frac{\phi}{\pi\times R-{1}^{2}}$$\Leftrightarrow$$v_{1}=\frac{0,0283}{\pi\times{(0,15)}^{2}}$
$$\color{Sepia}{v_{1}= 0,40\,m/s}$$
$v_{2}=\frac{\phi}{\pi\times R_{2}^{2}}$$\Leftrightarrow$$v_{2}=\frac{0,0283}{\pi\times{(0,05)}^{2}}$
$$\color{Sepia}{v_{2}=3,6\,m/s}$$
Para a água, teremos:
$p_{1} + \frac{\mu\times v_{1}^{2}}{2} = p_{2} + \frac{\mu\times v_{2}^{2}}{2} + \Delta p$$\Leftrightarrow$$20,58\times {10}^{4} + \frac{{10}^{3}\times{0,4}^{2}}{2} = p_{2} + \frac{{10}^{3}\times{3,6}^{2}}{2} + 2,058\times{10}^{4}$
$20,58\times{10}^{4} + {{10}^{3}\times 0,08} = p_{2} + {10}^{3}\times {6,48} +2,058\times{10}^{4}$
$20,588\times{10}^{4} – 0,648\times{10}^{4} – 2,058\times{10}^{4}= p_{2}$
$20,588\times{10}^{4} – 2,706\times{10}^{4} = p_{2}$$\Leftrightarrow$$p_{2} = 17,882\times{10}^{4}\,Pa$
Temos que:$1\,N/m^{2} = \frac{1}{9,8}\,kgf/m^{2}=\frac{{10}^{-4}}{9,8}\,kgf/cm^{2}$
Assim: $p_{2} = \frac{17,882\times{10}^{4}}{9,8\times{10}^{-4}}$$p_{2}= \frac{17,882\times{10}^{4}\times{10}^{-4}}{9,8}$
$$\color{Navy}{p_{2} = 1,824\,kgf/cm^{2}}$$
Para o óleo de densidade $\delta = 0,8$.
$p_{1} + \frac{0,8\times{10}^{3}\times{v_{1}^{2}}}{2} = p_{2} + \frac{0,8\times{10}^{3}\times{v_{2}^{2}}}{2} + \Delta p$
$20,58\times{10}^{4} + \frac{0,8\times{10}^{3}\times{0,4}^{2}}{2} = p_{2} + \frac{0,8\times{10}^{3}\times{3,6}^{2}}{2} + 2,058\times{10}^{4}$
$20,58\times{10}^{4} + 0,064\times{10}^{3} = p_{2} + 5,184\times{10}^{3} + 2,058\times{10}^{4}$$\Leftrightarrow$$20,5864\times{10}^{4} – 2,5764\times{10}^{4} = p_{2}$
$p_{2} = 18,100\times{10}^{4}\,Pa$
Usando o mesmo raciocínio de antes, convertemos em $kgf/cm^{2}$.
$$\color{Navy}{p_{2} = \frac{18,100\times{10}^{4}\times{10}^{-4}}{9,8} = 1,847\,kgf/cm^{2}}$$
08. Um tubo de Pitot é montado na asa de um avião, para determinar a velocidade da aeronave em relação ao ar. O tubo contém mercúrio ($\mu_{Hg} = 13,6 · 10^{3}\,kg/m^{3}$) e indica uma diferença de nível de $h=11\,cm$. Considerando que $g = 10\, m/s^{2}$ e que a densidade do ar seja $\delta_{ar} = 1,29$, qual é a velocidade do avião em relação ao ar, em $km/h$?
$$\color{Navy}{v = \sqrt{\frac{2\mu_{Hg}gh}{\mu_{gás}}}}$$
$v = \sqrt{2\times{13,6}\times{10}^{3}\times {10}\times {0,11}}{1,29} = \sqrt{2,32\times{10}^{1}}$
$v = {1,523}\times{10}^{2}=152,3\,m/s$
$$\color{Navy}{v = 152,3\times{3,6}=548,2\,km/h}$$
Exercícios para resolver
01. 0 diâmetro de uma tubulação inclinada aumenta gradualmente de $D_{A}=150\,mm$ em A, para $D_{B}=450\,mm$ em B, estando A a $4,5 m$ abaixo de B. Se a pressão em A for de $p_{A}=0,7\,kgf/cm^{2}$ e em B de $p_{B}=0,490\,kgf/cm^{2}$, e a descarga de $\phi=140,0\, l/s$, quais são:
a) o sentido do escoamento?
b) a perda por atrito entre os dois pontos?
02. Calcule a perda de carga no trecho A-B da canalização da figura abaixo. Dados:
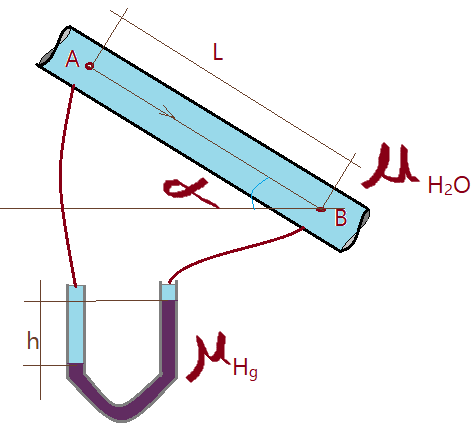
a)Líquido em escoamento = óleo (d = 0,8);
b)Líquido manométrico = Hg (d = 13,6).
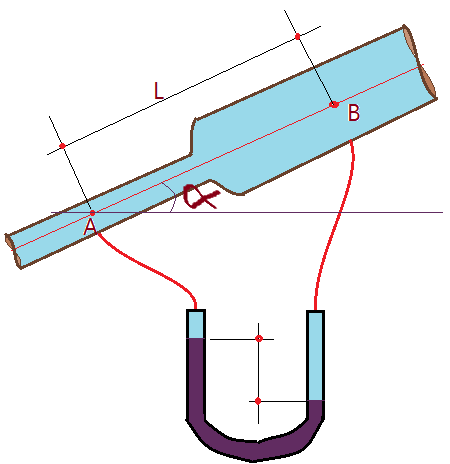
03. A canalização inclinada AB, esquematizada na figura abaixo, é composta por 2 trechos de diâmetro $D_{A}= 50\,mm$ e $D_{B}=75\,mm$. Analisando a deflexão da coluna de mercúrio do manômetro diferencial, cujo líquido manométrico é mercúrio, cuja densidade vale $\mu_{Hg}=13,6\,g/m^{3}$ e sabendo-se que a canalização conduz água a uma vazão de $\phi = 5\,l/s$, determine o sentido do escoamento e a perda de carga no trecho AB.
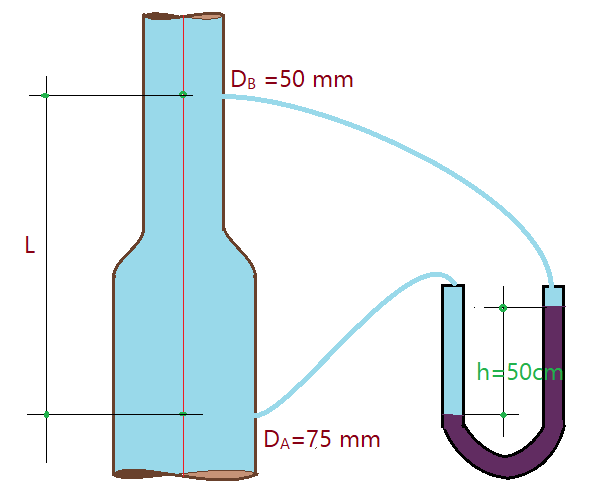
04. Calcule a perda de carga no trecho A-B da canalização vertical da figura abaixo, e diga qual é o sentido do fluxo, sabendo-se que a vazão escoada é de $\phi = 5 l/s$. Líquido manométrico é $\delta_{Hg}=13,6$.
05. Calcular a vazão nos 3 venturímetros esquematizados na figura abaixo, suponha que não há perdas.
Dados: – diâmetro da canalização $D = 100\,mm$;
– diâmetro da seção estrangulada $d = 50\,mm$;
– líquido em escoamento = $H_{2}O$;
– líquido manométrico = Hg ($\delta_{Hg}=13,6$)
– deflexão “h” da coluna de mercúrio $h= 20\,cm$.
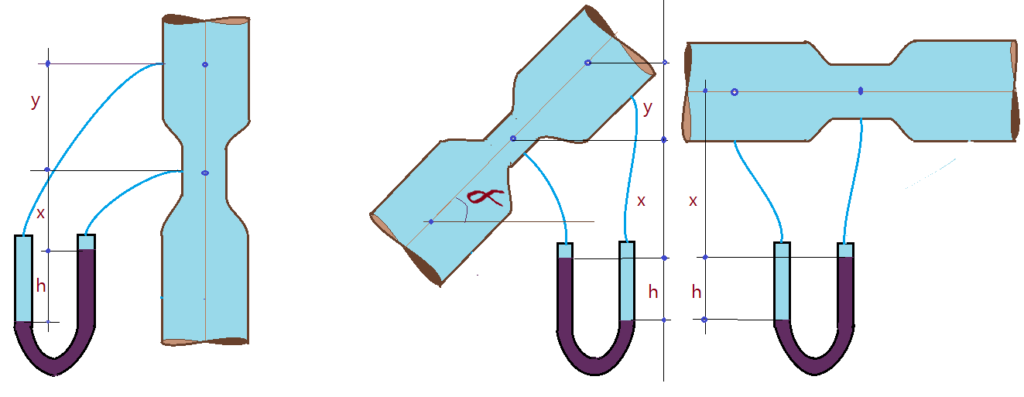
06. Ao longo de uma tubulação de $D=150\,mm$ de diâmetro encontra-se um venturímetro ligado a um manômetro diferencial e a dois piezômetros. Sabendo-se que a velocidade na tubulação 1 de $v_{1}= 2\,m/s$, a pressão no ponto (1) é de $p_{1}=2,5\,kgf/cm^{2}$ e o líquido manométrico é o mercúrio com densidade relativa igual a $\delta = 13,6$. O diâmetro no estrangulamento é $D_{2}=100\,mm$.
Calcular, desprezando as perdas de carga:
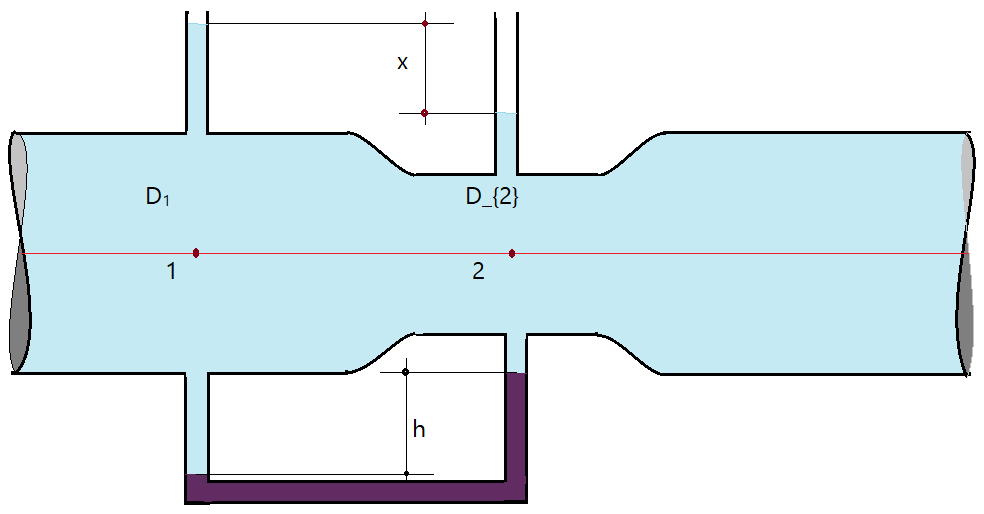
a) a pressão no ponto (2);
b) a altura h (cm.c.Hg);
C) a altura x.
07. Um venturímetro de $D_{2}=150\,mm$ no estrangulamento, intercala-se numa canalização d’água de $D_{1}=450\,mm$. Na escala diferencial parcialmente cheia de Hg (estando o resto cheio d’água), e ligada à boca e à cintura do medidor, a coluna mercurial estabiliza-se com um desnível de 375 mm. Calcule a vazão:
a) desprezando o atrito;
b) considerando uma perda de carga entre a boca e a cintura de 300 mm de água.
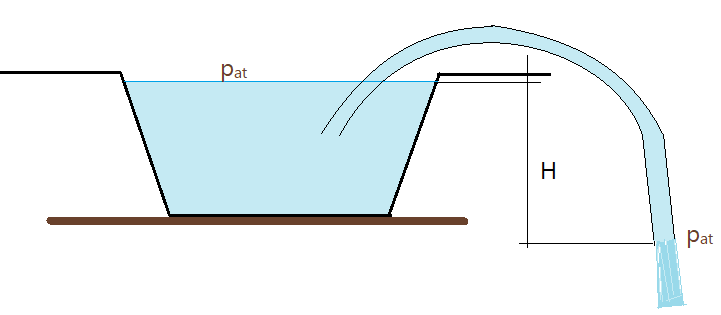
08. Calcule a altura H da figura abaixo, para que o sifão de 1 polegada forneça uma vazão de $\phi=1,0\,l/s$. (Despreze as perdas).
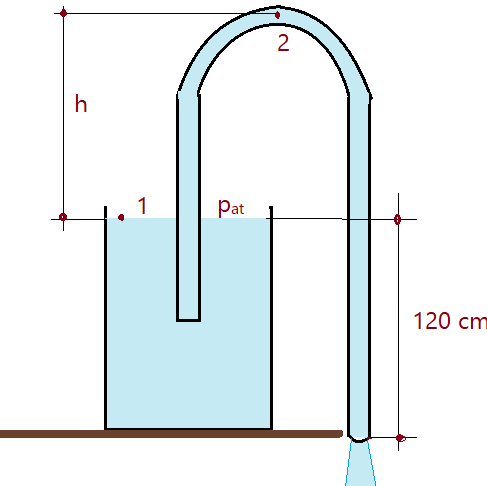
09. Desprezando-se as perdas, calcular o valor máximo de “h” na figura abaixo, para que a pressão absoluta no ponto 2 não seja menor que $p_{2}\ge 0,25\,kgf/cm^{2}$, sabendo-se que a pressão barométrica local é de $p_{atm}=10\,m.c.a.$.
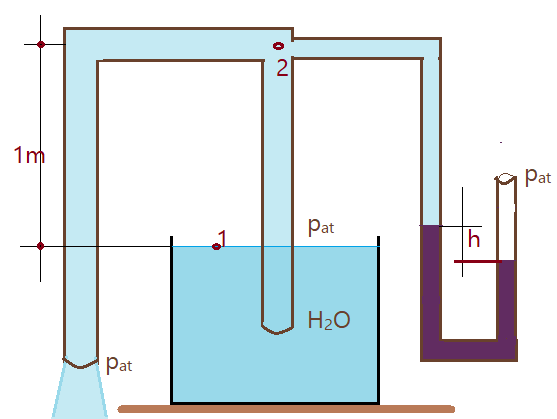
10. Um sifão de$D_{S}=6″$ polegadas conduz uma vazão de $\phi=40\,l/s$. Calcule a deflexão da coluna de mercúrio H do tubo em “U” que está conectado no ponto 2, situado a 1 m acima do nível da água, como mostra a figura abaixo. (Despreze as perdas).
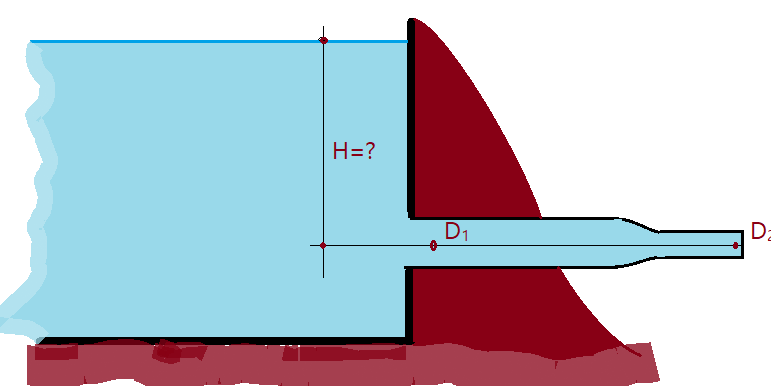
11. De uma pequena barragem, parte uma canalização de $D_{1}=25\,mm$ de diâmetro, com poucos metros de extensão, havendo posteriormente uma redução para $D_{2}=125\,mm$. Do tubo de $D_{1}=125\,mm$, a água parte para a atmosfera em forma de jato. A vazão foi medida, encontrando-se o valor de $\phi=105\,l/s$. Desprezando-se as perdas, calcular a pressão na seção inicial da tubulação de 250 mm e a altura de água na barragem, da superfície ao eixo da canalização.
12. Uma canalização que conduz uma vazão de $\phi=140\,l/s$, descarrega a $h_{p}=1,80\,m$ de profundidade, num reservatório. 0 diâmetro da canalização na extremidade de descarga é de $D_{2}=300\,mm$. Calcular a pressão num ponto A localizado $h_{1}=1,20\,m$ acima do nível d’água, onde a canalização apresenta diâmetro igual a $D_{1}=250\,mm$, desprezando as perdas de energia.
13. Um orifício lateral de um grande tanque, como o da Fig, abaixo descarrega água. Sua reação é circular, de $50\,mm$ de diâmetro, sendo jato de igual dimensão. Mantêm-se o Nível d’água no reservatório $h=3,80\,m$ acima do centro do jato. Calcular a descarga :
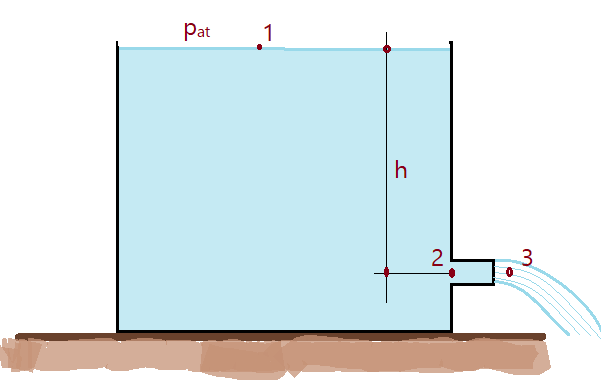
a) desprezando a perda de carga;
b) supondo-a 10% de h = 3,80 m.
14. Um jardineiro dispõe de mangueiras de dois tipos, porém com a mesma vazão. Na primeira, a água sai com velocidade de módulo V e, na segunda, sai com velocidade de módulo 2V. A primeira mangueira apresenta:
a) a metade da área transversal da segunda;
b) o dobro da área transversal da segunda;
c) um quarto da área transversal da segunda;
d) o quádruplo da área transversal da segunda;
e) dois quintos da área transversal da segunda.
15. Um fluido ideal percorre um cano cilíndrico em regime permanente. Em um estrangulamento onde o diâmetro do cano fica reduzido à metade, a velocidade do fluido fica:
( )a) reduzida a 1/4;
( )b) reduzida à metade;
( )c) a mesma;
( )d) duplicada;
( )e) quadruplicada.
16. Durante uma tempestade, Maria fecha a janela de seu apartamento e ouve zumbido do vento lá fora. Subitamente o vidro de uma janela se quebra. Considerando que o vento tenha soprado tangencialmente à janela, o acidente pode ser melhor explicado pelo(a):
( )a) princípio da conservação da massa;
( )b) equação de Bernoulli;
( )c) princípio de Arquimedes;
( )d) princípio de Pascal;
( )e) princípio de Stevin.
17. Um menino deve regar o jardim de sua mãe e pretende fazer isso da varanda de sua residência, segurando uma mangueira na posição horizontal, conforme a figura. Durante toda a tarefa, a altura da mangueira, em relação ao jardim, permanecerá constante. Inicialmente a vazão de água, que pode ser definida como o volume de água que atravessa a área transversal da
mangueira na unidade de tempo, é $t_{o}$. Para que a água da mangueira atinja a planta mais distante no jardim, ele percebe que o alcance inicial deve ser quadruplicado. A mangueira tem em sua extremidade um dispositivo com orifício circular de raio variável. Para que consiga molhar todas as plantas do jardim sem molhar o resto do terreno, ele deve:
( )a) reduzir o raio do orifício em 50% e quadruplicar a vazão de água;
( )b)manter a vazão constante e diminuir a área do orifício em 50%;
( )c) manter a vazão constante e diminuir o raio do orifício em 50%;
( )d) manter constante a área do orifício e dobrar a vazão da água;
( )e) reduzir o raio do orifício em 50% e dobrar a vazão de água.
18. A artéria aorta de um adulto tem um raio de cerca de $R=1,0\,cm$, e o sangue nela flui com velocidade de $v=33,0\,cm/s$.
a) Quantos litros de sangue são transportados pela aorta por segundo?
b) Sendo de $V=5\,l$ o volume de sangue no organismo, use o resultado anterior para estimar o tempo médio que o sangue demora a retornar ao coração.
19. Um medidor de Venturi tem diâmetro de $D_{1}=10\,cm$ no tubo e de $D_{2}=5,0\,cm$ no estreitamento. A pressão da água no tubo é de $p_{1}= 0,85\,atm$ e no estreitamento é de $p_{2}=0,35\, atm$. Determine a vazão de água em $l/s$. Considere $1\,atm = 1,0\times 10^{5}\,N/m^{2}$ e $\mu_{H_{2}O}=1,0\times 10^{3}\,kg/m^{3}$.
20. Uma asa de avião tem área de $S = 5\, m^{2}$ e massa de $m = 200\,kg$. A velocidade do fluxo de ar acima da face superior é de $V_{2}=70\,m/s$ e sob a face inferior, $v_{1} = 50\,m/s$. Considere que a massa específica do ar seja igual a $\mu_{ar} =1,29\,kg/m^{3}$ e adote $g = 10\,m/s^{2}$. Determine:
a) a diferença de pressão entre a face superior e a face inferior da asa;
b) a força de sustentação da asa;
c) a força resultante na asa.
21. (U.F.Juiz de Fora-MG) Na figura abaixo representamos um objeto de perfil triangular dentro de um túnel de vento. A área total do túnel de vento é $S_{t} =2A$, e a área acima do topo da secção triangular é S_{2}=B$. Admitindo que o escoamento do ar é estacionário e que este se comporta como um fluido ideal (incompressível, sem atrito), responda às questões
abaixo.
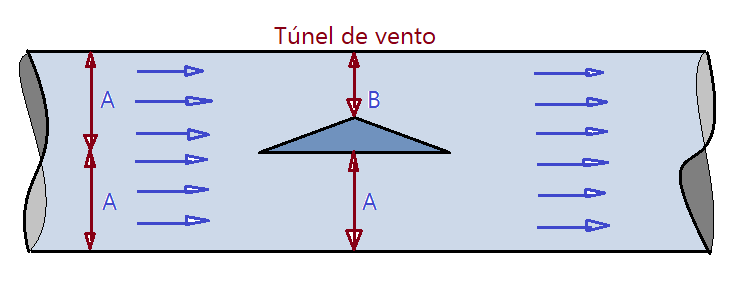
a)Sendo $p_{1}$ a pressão abaixo do perfil e $p_{2}$ acima, qual a relação entre elas?
b) por causa da diferença de pressão, qual é o sentido da força resultante sobre o perfil?
c) qual a influência da altura do perfil no valor da diferença de pressão?
d) onde a velocidade de escoamento do vento é menor?
22. (UFPA) Em 5 minutos, um carro-tanque descarrega $V=5.000 l$ de gasolina através de um mangote, cuja secção transversal tem área igual a $S_{m}=0,00267\,m^{2}$ (ver figura abaixo).
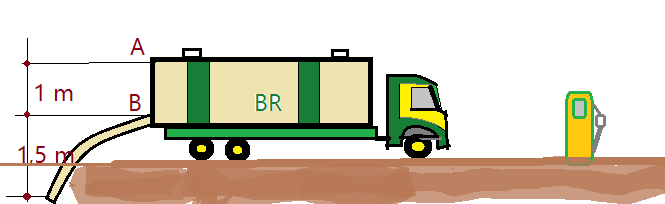
Pergunta-se:
a) Qual a vazão volumétrica média desse escoamento, em litros/segundo?
b) Considerando os dados indicados na figura e $g = 9,8\,m/s^{2}$, qual a vazão volumétrica, em litros/segundo, no início do processo de descarga do combustível, quando o nível de líquido no tanque está no ponto A?
c) O valor obtido no item b deve ser maior, menor ou igual ao do item a?
23. Uma bomba de recalque é usada para bombear água para fora de um navio. A mangueira da bomba tem um diâmetro de $D_{m}=3,0\,cm$ e a bomba drena a água, através da mangueira, até a saída, $h= 5\,m$ acima da linha-d’água, abandonando-a com velocidade de $V = 4,0\,m/s$. Adote para a água $\mu_{H_{2}O} = 10^{3}\,kg/m^{3}$ e considere $1\,hp = 746\,W$.
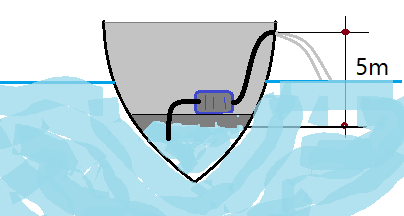
Determine:
a) a vazão de água através da mangueira;
b) a diferença de pressão fornecida pela bomba de recalque;
c) a potência da bomba.
24. Desprezando-se as perdas, calcular a vazão no esquema abaixo:
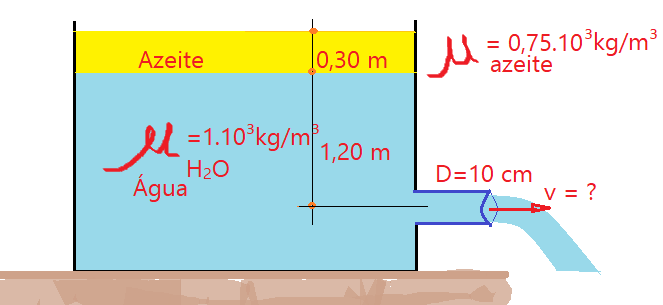
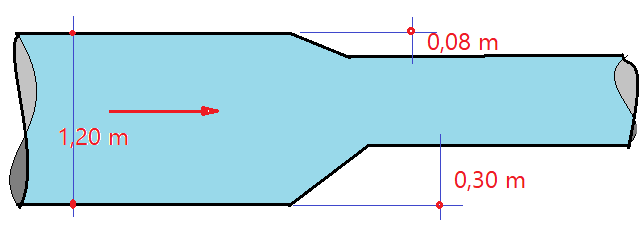
25. A largura de um canal retangular reduz-se de $L_{1}= 1,8\,m$ a $L_{2}= 1,5\,m$ e o fundo eleva-se de $\Delta p=0,3\,m$ da primeira à segunda seção, conforme a figura abaixo. A profundidade da primeira seção é de $p_{1}=1,2\,m$ e o rebaixamento da superfície livre até a segunda é de $\Delta h=0,08\,m$. Determinar a vazão da água no canal, desprezando-se as perdas.
Há variada escolha de exercícios desse assunto à disposição em diversos sites da internet se tiver dificuldades na resolução, use um dos canais abaixo para contato e expor sua dúvida. Estou ao seu dispor para esclarecer e ajudar a buscar o entendimento.
Curitiba, 16 de agosto de 2020.
Décio Adams
www.facebook.com/livros.decioadams
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
