FI.ME.017-01- Física-Mecânica. Hidrostática II
Vimos nas páginas do post anterior as principais questões teóricas e algumas aplicações sobre o assunto. Ainda há o que falar a respeito disso e vamos a algumas coisas importantes ou interessantes, curiosas até.
Forma de barragens.
As barragens das hidrelétricas e captações de água para tratamento urbano, têm hoje técnicas avançadas de construção, visando economia de material, aumento da capacidade de acumulação, solidez da construção e durabilidade. Não devemos pensar que uma barragem como é o caso de Itaipu, Três Marias, Quedas do Iguaçu e tantas outras são meros paredões que impedem a água de passar. A solidez da obra deve ter em conta as características do solo onde é implantada, a altura e principalmente a forma das faces. O lado de “montante”, onde a água é represada, tem em geral um talude superior de mais ou menos $45^{0}$ de inclinação em relação à vertical, acontecendo o mesmo na face de “jusante”, isto é o outro lado da barragem.
Qual é a vantagem dessas inclinações? Sabemos que a pressão é sempre normal à superfície. Dessa forma, a inclinação resulta em uma força na mesma direção, diminuindo a componente horizontal. Dessa forma a estrutura torna-se mais resistente à força da água que retém. Dependendo da conformação geográfica do local, a construção pode ser feita em forma de curva, acrescentando um fator de redução da força, já que estas em cada ponto tem a direção do raio de curvatura. Não pretendo aqui ensinar a construir barragens, pois isso é tarefa que cabe aos engenheiros especializados no assunto. O avanço tecnológico alcançado nos dias atuais, permite um aumento da solidez desse tipo de construção, com consequente economia de material e tempo.
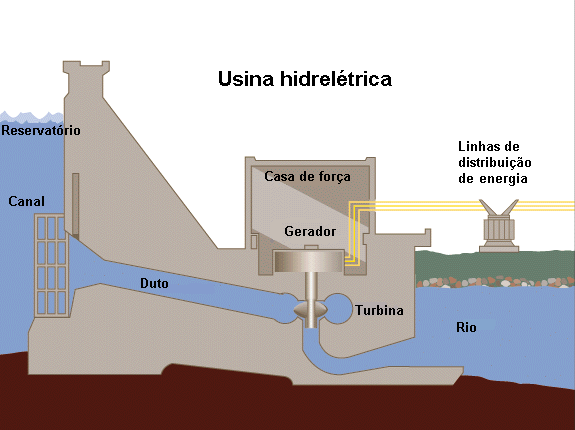

Percebemos que não há verticalidade nas faces das barragens. A face inclinada pode ser com enrocamento, onde se usa uma base de pedras recoberta de concreto armado, especialmente na face a montante. Há uma região oca no interior da imensa “muralha”, onde estão instalados instrumentos de monitoramento e pontos de inspeção da estrutura.
Paradoxo hidrostático.
Vamos imaginar vários recipientes de diferentes formas e capacidades volumétricas, como mostra a figura.
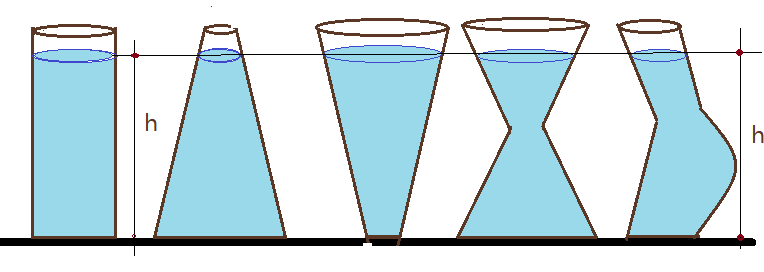
Olhando os recipientes da figura vemos facilmente que as quantidades de líquido que eles contém são diferentes. Sendo todos os conteúdos do mesmo líquido e atingindo a mesma altura, o que se pode dizer relativamente as pressões que o líquido exerce sobre o fundo de cada recipiente?
A primeira impressão que temos é que, quanto maior o peso do líquido e menor a área da superfície no fundo, maior será a pressão. Mas será isso verdadeiro?
Voltemos ao Princípio de Stevin.
$$\color{Maroon}{p = p_{at} + \mu_{l}\times g\times h}$$
Essa equação nos informa que a pressão sobre o fundo independe da área da superfície, do peso do líquido e é igual em todos os recipientes. Como essa realidade aparentemente contradiz a lógica, chamamos esse fato de Paradoxo hidrostático.
Copo de Pitágoras
O filósofo e matemático Pitágoras criou um copo aparentemente igual a muitos outros copos. A figura mostra um copo desse tipo cortado ao meio mostrando os detalhes.
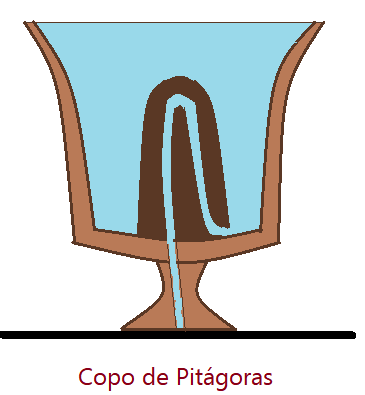
Observamos que no interior existe uma estrutura que atinge um pouco mais da metade da altura interna do copo. No interior dessa estrutura e prolongando-se até a base, existe um tubo, que se abre no fundo do copo.
Ao enchermos o copo com um líquido, esse sobe pelo tubo, como acontece nos vasos comunicantes. Ao atingir a um nível acima do tupo, o líquido inicia o escoamento pelo tubo. Mesmo que seja enchido até a borda do copo, o efeito sifão do tubo faz o líquido escoar totalmente, não restando nada no interior do copo.
É possível reproduzir esse efeito com apenas um tubo e o copo, bastando que a abertura do tubo fique no fundo e depois suba até além da metade, descendo então até a base no lado externo.
Esse procedimento usamos toda vez que precisamos retirar de um tambor uma certa quantidade de líquido, dispondo para isso de um tubo (mangueira). Introduzimos uma extremidade do tubo no líquido e sugamos forte na outra extremidade. Depois que o tubo fica cheio de líquido podemos colocar a extremidade livre num nível mais baixo do que o do líquido e o efeito “sifão” faz o serviço de retirar o líquido para nós.
Peso aparente
Usando um dinamômetro, podemos determinar o peso de um corpo. O que acontecerá se depois mergulharmos o corpo em um líquido (água por exemplo), mantendo-o suspenso pelo dinamômetro?
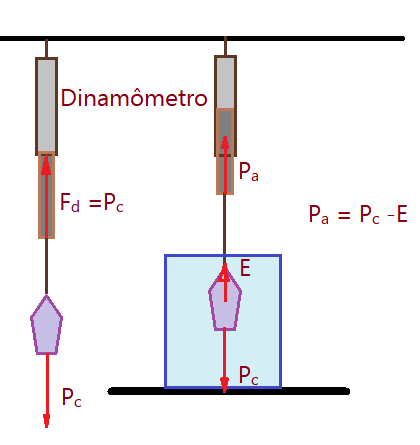
Olhando a figura, vemos que o dinamômetro passa a indicar um valor diferente, menor que o primeiro. Esse peso é denominado Peso aparente. Seu valor, subtraído do peso do corpo, nos fornece o valor do empuxo que o líquido exerce sobre o corpo, em conformidade com o Princípio de Arquimedes.
$$\color{Navy}{P = \mu\times V\times g }$$
$P_{a} = P – E = \mu_{c}\times V\times g – \mu_{l}\times V\times g$
$$\color{Navy}{P_{a} = V\times g{(\mu{c} – \mu_{l})}}$$
Isso é possível?
A figura a seguir mostra um copo cheio de água até a borda na primeira posição. Depois ele aparece virado de boca para baixo, tampado apenas com uma folha de papel. Qual é o fenômeno que possibilita isso? Ou isso é impossível?
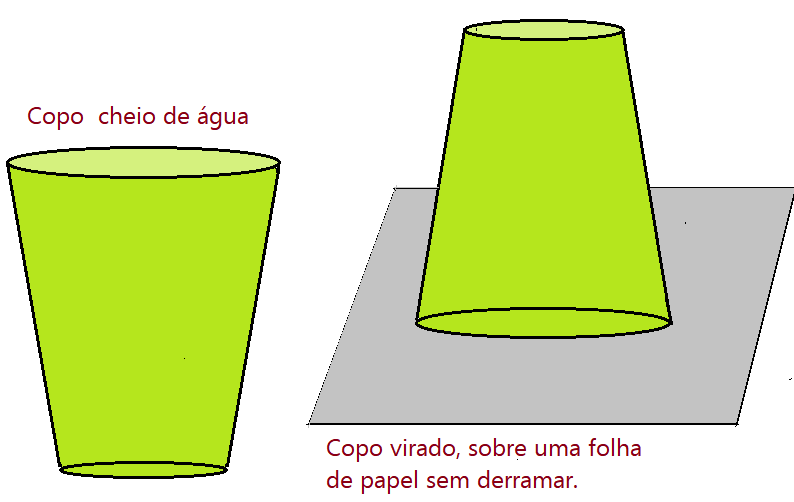
Estando o copo completamente cheio e colocando sobre ele uma folha de papel, basta segurar o papel com a mão esquerda espalmada e virar o copo com a outra mão. Não havendo entrada de ar, a pressão atmosférica sobre a folha de papel é maior que a pressão da água que há dentro do copo. A função da mão segurando o papel ao virar é mantê-lo na posição e não permitir a entrada de ar.
A natureza tem horror ao vácuo?
O filósofo e matemático grego Aristóteles deixou estabelecida uma convicção:
“A natureza tem horror ao vácuo”.
A interpretação dessa afirmação é de que, toda vez que houvesse, em algum ponto do Universo, uma tendência de se estabelecer o vácuo, os corpos e substâncias circundantes se apressariam em ocupar o espaço vazio para impedir a formação do vácuo. Como ninguém se propôs a contestar e provar o contrário, ela ficou valendo até ao final da Idade Média.
Era comum usar nessa época bombas de sucção para retirar água de poços, porém de pouca profundidade. Em determinado momento o famoso “horror ao vácuo” parece ter parado de existir, especialmente quando os poços eram de profundidades superiores aos 10,0 m. As bombas de sucção não eram capazes de extrair uma gota de água desses poços. Isso ocorre na era em que Galileu Galilei era um dos maiores matemáticos e físicos da Itália. Os construtores, injuriados com a negativa da água em subir além dessa altura, foram pedir explicações ao cientista. Evangelista Torricelli e outro seu colega eram alunos de Galileu. Ele lhes deu o encargo de descobrir a razão da negativa da natureza (água) em cumprir o “horror ao vácuo”. Galileu teria dito em tom de brincadeira:
- Talvez a natureza tenha perdido seu horror ao vácuo!
Os dois discípulos provaram que existia a pressão atmosférica, fenômeno ao qual se devia a elevação da água pelas bombas até a altura de pouco mais de 10 m. Bastava comparar as colunas de água e mercúrio que eram capazes de equilibrar a pressão atmosférica.
$p_{at} = \mu_{Hg}\times g\times h_{Hg} = \mu_{H_{2}O}\times g\times h_{H_{2}O}$
${13,6}\times\not{g}\times {0,76} = 1\times\not{g}\times h{H_{2}O}$
$$\color{Brown}{h_{H_{2}O} = {13,6}\times {0,76} = 10,333\,m}$$
É necessário uma coluna de água com altura de mais de dez metros para equilibrar a pressão atmosférica. Essa é a razão de as bombas de sucção funcionarem até essa profundidade. As variações são devidas ao desnível em relação ao do mar, onde o valor é o de referência.
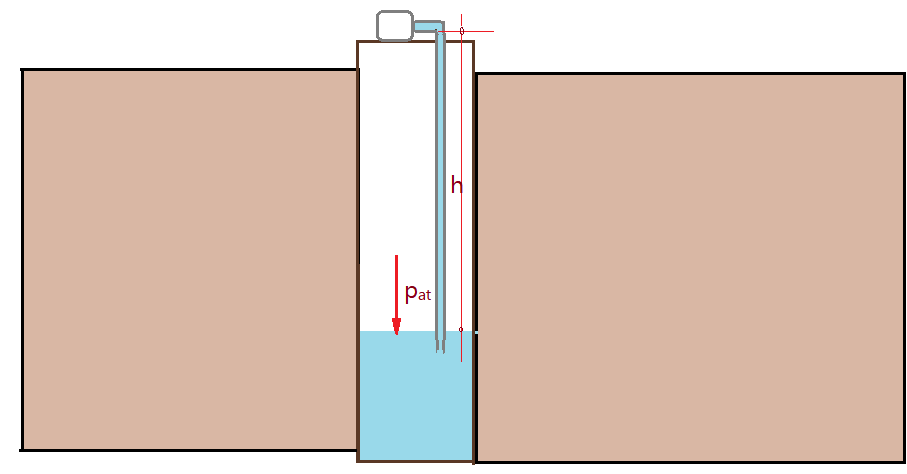
Posteriormente foi inventado um dispositivo adicional, que permite a esse tipo de bomba retirar água de profundidades maiores. Basta adicionar ao cano por onde a água sobe, outro recheado e tendo na extremidade um dispositivo de válvula, conhecido como injetor. Assim fica possível compensar a insuficiência da pressão atmosférica.
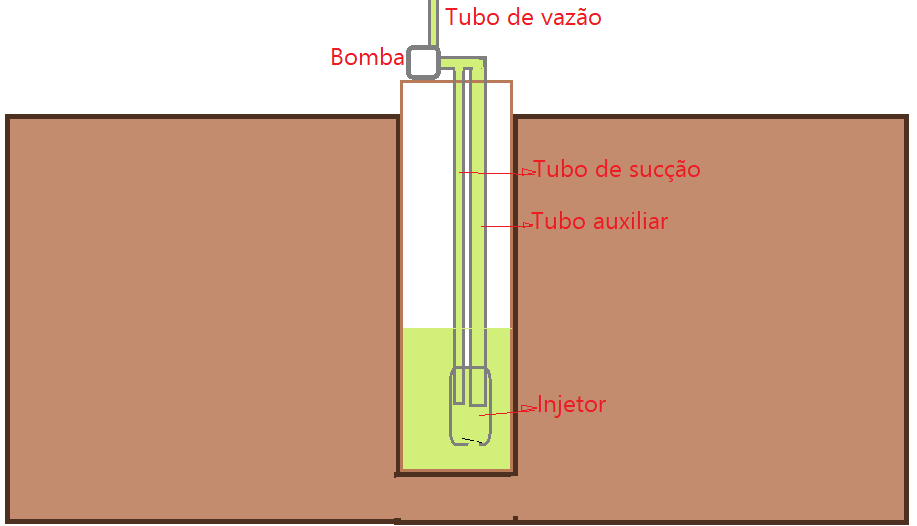
Nesta nova figura vemos um tubo de diâmetro maior e na extremidade inferior os dois estão ligados ao injetor. Na base desse existe a válvula que permite a entrada de água nova para ser enviada ao reservatório externo. A sucção da bomba provoca a abertura da válvula e a entrada de água. Usa-se a própria coluna de água do tubo auxiliar para ajudar no processo. Funcionam como vasos comunicantes.
Coube a Blaise Pascal realizar experimentos em diversos lugares usando água, vinho e óleo para determinar as equivalências das alturas em relação ao mercúrio.
Consta nos livros que a água exigiu uma coluna de 10 m, o vinho em torno de 15 m. Fez suas experiências na cidade de Ruão. O óleo, com densidade em torno de $\delta = 0,8$ alcançou uma altura próxima dos 12,0 m.
Exercícios de vestibulares.
01. (UNIPAC) – Uma prensa hidráulica possui pistões com diâmetros $d_{1}=8\,cm$ e $d_{2}= 24\,cm$. Se uma força de $F= 120\,N$ atua sobre o pistão menor, pode-se afirmar que esta prensa estará em equilíbrio quando sobre o pistão maior atuar uma força de:
( )a) $300\,N$;
( )b) $360\,N$;
( )c) $1080\,N$;
( )d) $540\,N$;
( )e) $120\,N$.
02.(UFLA) – O empuxo exercido sobre um corpo imerso em um líquido depende:
( )a) do volume do líquido deslocado e da densidade do corpo;
( )b) da densidade e do volume do corpo;
( )c) do volume e da densidade do líquido deslocado;
( )d) somente do volume do líquido deslocado;
( )e) somente da densidade do líquido deslocado.
03. (UFV) – Uma lata tampada com dois orifícios encontra-se parada, imersa em um recipiente com água. O orifício superior comunica-se com o exterior através de uma mangueira. Ao injetarmos ar pela mangueira, é correto afirmar que a lata:
( )a) afundará;
( )b) subirá;
( )c) aumentará de peso;
( )d) permanecerá parada;
( )e) receberá ar pelo orifício inferior.
04. (UFPEL-RS) – A expressão “Isso é apenas a ponta de um iceberg” – muito usada conotativamente, hoje em dia, para mostrar que se vê apenas uma parte muito pequena de um problema, ficando o resto “escondido” – faz referência a uma situação física.
Assinale a alternativa cujos dados se relacionam corretamente com essa situação.
( )a) o Poder das Pontas e a Rigidez Dielétrica;
( )b) Arquimedes e o Teorema do Empuxo;
( )c) Pascal e o Princípio da Prensa Hidráulica;
( )d) Newton e o Princípio da Ação e Reação;
( )e) A Lei de Stevin e a Diferença de Pressão.
05.(PUC-RS) – No oceano a pressão hidrostática aumenta aproximadamente uma atmosfera a cada $10\,m$ de profundidade. Um submarino encontra-se a $300\, $m de profundidade, e a pressão do ar no seu interior é de uma atmosfera. Nesse contexto, pode-se concluir que a diferença da pressão entre o interior e o exterior do submarino é, aproximadamente, de
( )a) 200 atm;
( )b) 100 atm;
( )c) 31 atm;
( )d) 30 atm;
( )e) 29 atm.
06. (UFG) – Em um recipiente contendo $100\,mL$ o que equivale a $1,37\,kg$ de mercúrio líquido, são colocados dois cubos (A e B), com volumes de $V_{1}= V_{2} = 2\,cm^3$ cada, de um material inerte diante do mercúrio. Os cubos têm massas de $m_{1}=14\,g$ e $m_{2}=24,0\,kg$, respectivamente.
Ao serem colocados no recipiente,
( )a) os cubos vão para o fundo;
( )b) o cubo A afunda e o B flutua;
( )c) o cubo B afunda e o A flutua;
( )d) os cubos flutuam a meio caminho do fundo;
( )e) os cubos ficam na superfície do líquido.
07. (Enem) – Um dos problemas ambientais vivenciados pela agricultura hoje em dia é a compactação do solo, devida ao intenso tráfego de máquinas cada vez mais pesadas, reduzindo a produtividade das culturas. Uma das formas de prevenir o problema de compactação do solo e substituir os pneus dos tratores por pneus mais
( )a) largos, reduzindo pressão sobre o solo;;
( )b) estreitos, reduzindo a pressão sobre o solo;
( )c) largos, aumentando a pressão sobre o solo;
( )d) estreitos, aumentando a pressão sobre o solo;
( )e) altos, reduzindo a pressão sobre o solo.
08. (UESPI) – Um recipiente contendo $V =300\,mL$ de água foi esquecido em um freezer por cerca de 7 horas. Após este tempo, quando a porta do freezer foi aberta, percebeu-se que
( )a) o volume havia aumentado devido ao aumento da densidade da água quando no estado sólido em relação à água líquida;
( )b) o volume havia diminuído devido à diminuição da densidade da água quando no estado sólido em relação à água líquida;
( )c) o volume havia diminuído devido ao aumento da densidade da água quando no estado sólido em relação à água líquido;
( )d) o recipiente permanecia como o mesmo volume, pois a densidade da água não aumentou nem diminuiu;
( )e) o volume havia aumentado devido à diminuição da densidade da água quando no estado sólido em relação à água líquida.
09. (ACAFE-SC) – Um prego é colocado entre dois dedos, que produzem a mesma força, de modo que a ponta do prego é pressionada por um dedo e a cabeça do prego pela outra. O dedo que pressiona o lado da ponta sente dor em função de:
( )a) a pressão ser inversamente proporcional à área para uma mesma força;
( )b) a força ser diretamente proporcional à aceleração e inversamente proporcional à pressão;
( )c) a pressão ser diretamente proporcional à força para uma mesma área;
( )d) a sua área de contato ser menor e, em conseqüência, a pressão também;
( )e) o prego sofrer uma pressão igual em ambos os lados, mas em sentidos opostos.
10. (UNISA) – Três pessoas A, B e C de mesmo peso e altura diferentes usam: A, o mais baixo, patins para gelo; B, o de altura intermediária, patins normais com rodas e C, o mais alto, sapato de couro normal. Determine qual exerce maior pressão sobre o solo.
( )a) PA = PB = PC;
( )b) PC > PB > PA;
( )c) PA = PB > PC;
( )d) PA > PB > PC;
( )e) PA < PB = PC.
11. (ITA) – Um pedaço de gelo flutua em equilíbrio térmico com uma certa quantidade de água depositada em um balde. À medida que o gelo derrete, podemos afirmar que
( )a) o nível da água no balde aumenta, pois haverá uma queda de temperatura da água;
( )b) o nível da água no balde diminui, pois haverá uma queda de temperatura da água;
( )c) o nível da água no balde aumenta, pois a densidade da água é maior que a densidade do gelo;
( )d) o nível da água no balde diminui, pois a densidade da água é maior que a densidade do gelo;
( )e) o nível da água no balde não se altera.
12. (UFRS) – A atmosfera terrestre é uma imensa camada de ar, com dezenas de quilômetros de altura, que exerce uma pressão sobre os corpos nela mergulhados: a pressão atmosférica.
O físico italiano Evangelista Torricelli (1608-1647), usando um tubo de vidro com cerca de 1 m de comprimento completamente cheio de mercúrio, demonstrou que a pressão atmosférica ao nível do mar equivale à pressão exercida por uma coluna de mercúrio de 76 cm de altura. O dispositivo utilizado por Torricelli era, portanto, um tipo de barômetro, isto é, um aparelho capaz de medir a pressão atmosférica.
A esse respeito, considere as seguintes afirmações.
I – Se a experiência de Torricelli for realizada no cume de uma montanha muito alta, a altura da coluna de mercúrio será maior que ao nível do mar.
II – Se a experiência de Torricelli for realizada ao nível do mar, porém com água, cuja densidade é cerca de 13,6 vezes menor que a do mercúrio, a altura da coluna de água será aproximadamente igual a 10,3 m.
III – Barômetros como o de Torricelli permitem, através da medida da pressão atmosférica, determinar a altitude de um lugar.
Quais estão corretas?
( )a) Apenas I;
( )b) Apenas II;
( )c) Apenas I e II;
( )d) Apenas II e III;
( )e) I, II e III.
13. (Enem) – Para oferecer acessibilidade aos portadores de dificuldade de locomoção, é utilizado, em ônibus e automóveis, o elevador hidráulico. Nesse dispositivo é usada uma bomba elétrica, para forçar um fluido a passar de uma tubulação estreita para outra mais larga, e dessa forma acionar um pistão que movimenta a plataforma. Considere um elevador hidráulico cuja área da cabeça do pistão seja cinco vezes maior do que a área da tubulação que sai da bomba. Desprezando o atrito e considerando uma aceleração gravitacional de $g =10\,m/s^{2}$, deseja-se elevar uma pessoa de $m= 65\,kg$ em uma cadeira de rodas de $m_{c}=15,0\,kg$ sobre a plataforma de $m_{p}=20\,kg$. Qual deve ser a força exercida pelo motor da bomba sobre o fluido, para que o cadeirante seja elevado com velocidade constante?
( )a) 20 N;
( )b) 100 N;
( )c) 200 N;
( )d) 1000 N;
( )e) 5000 N.
14.(UFPR) – Um reservatório cilíndrico de $h=2,0\,m$ de altura e base com área $S=2,4\,m^2$, como mostra a figura, foi escolhido para guardar um produto líquido de massa específica igual a $\mu = 1,2\,g/cm^3$. Durante o enchimento, quando o líquido atingiu a altura de $h_{p}=1,8\,m$ em relação ao fundo do reservatório, este não suportou a pressão do líquido e se rompeu. Com base nesses dados, assinale a alternativa correta para o módulo da força máxima suportada pelo fundo do reservatório.
( )a) É maior que 58.000 N;
( )b) É menor que 49.000 N;
( )c) É igual a 50.000 N;
( )d) Está entre 50.100 N e 52.000 N;
( )e) Está entre 49.100 N e 49.800 N.
15. (Enem) – Um tipo de vaso sanitário que vem substituindo as válvulas de descarga está esquematizado na figura. Ao acionar a alavanca, toda a água do tanque é escoada e aumenta o nível no vaso, até cobrir o sifão. De acordo com o Teorema de Stevin, quanto maior a profundidade, maior a pressão. Assim, a água desce levando os rejeitos até o sistema de esgoto. A válvula da caixa de descarga se fecha e ocorre o seu enchimento. Em relação às válvulas de descarga, esse tipo de sistema proporciona maior economia de água.
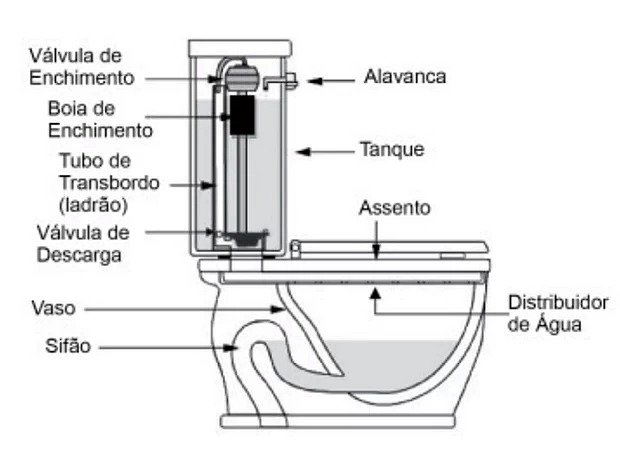
Faça você mesmo. Disponível em: http://www.facavocemesmo.net. Acesso em: 22 jul. 2010. (Foto: Reprodução/Enem)
A característica de funcionamento que garante essa economia é devida
( )a) à altura do sifão de água;
( )b) ao volume do tanque de água;
( )c) à altura do nível de água no vaso;
( )d) ao diâmetro do distribuidor de água;
( )e) à eficiência da válvula de enchimento do tanque.
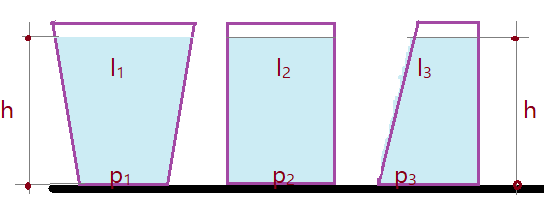
16. (UFMG-97) – A figura mostra três vasos $V_{1}, V_{2}, V_{3}$, cujas bases têm a mesma área. Os vasos
estão cheios de líquidos $l_{1}, l_{2}, l_{3}$ até uma mesma altura. As pressões no fundo dos vasos são $P_{1},
P_{2}, P_{3}$, respectivamente. Com relação a essa situação é correto afirmar que:
( )a) $P_{1} = P_{2} = P_{3}$ somente se os líquidos $l_{1}, l_{2}, l){3}$ forem idênticos;
( )b) $P_{1} = P_{2} = P_{3}$ quaisquer que sejam os líquidos $l_{1}, l_{2}, l_{3}$;
( )c) $P_{1} > P_{2} > P_{3}$ somente se os líquidos $l_{1}, l_{2}, l_{3}$ forem idênticos;
( )d) $P_{1} > P_{2} > P_{3}$ quaisquer que sejam os líquidos $l_{1}, l_{2}, l_{3}$;
( )e)$P_{1} < P_{2} < P_{3}$ quaisquer que sejam os líquidos $l_{1}, l_{2}, l_{3}$.
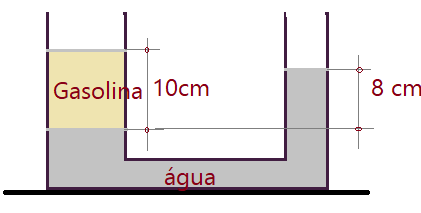
17. Um consumidor, desconfiado da qualidade da gasolina que comprou em um posto, resolveu
testar a sua densidade. Em um sistema de vasos comunicantes, contendo inicialmente água $(\mu_{H_{2}O} = 1\,g/cm^3)$, despejou certa quantidade da gasolina. Após o equilíbrio, o sistema adquiriu a aparência representada na figura. Determine a massa específica da gasolina comprada.
18 – Uma caixa de $P=500\,N$ tem faces retangulares e suas arestas medem $1,0\,m$, $2,0\,m$ e $3,0\,m$. Qual
a pressão que a caixa exerce quando apoiada com sua face menor sobre uma superfície horizontal?
( )a) $100\,N/m^{2}$;
( )b) $125\,N/m^2$;
( )c) $167\,N/m^{2}$;
( )d) $250\,N/m^{2}$;
( )e) $500\,N/m^{2}$.
19. O salto de um sapato masculino tem área de $S=64 cm^{2}$. Supondo-se.que a pessoa que o calce
tenha peso igual a $P=512\,N$ e que esse peso esteja distribuído apenas no salto, então a pressão
média exercida no piso vale:
( )a) $120\,kN/m^{2}$;
( )b) $80\,kN/m^{2}$;
( )c) $60\,kN/m^{2}$;
( )d) $40\,kN/m^{2}$;
( )e) $20\,kN/m^{2}$.
20. Uma pessoa com peso de $P=600\,N$ e que calça um par de sapatos que cobrem juntos uma área de $S=0,05\,m^{2}$, não consegue atravessar uma região nevada sem afundar, porque essa região não suporta uma pressão superior a $p=10.000\,N/m^{2}$. Responda:
a) Qual a pressão exercida por essa pessoa sobre a neve?
b) Qual deve ser a área mínima de cada pé de um esqui que essa pessoa deveria usar para não
afundar?
21. – Uma massa de $m= 1,0\,kg $ de água ocupa um volume de $V=1,0\,L $, a temperatura de $\theta= 40^0C$. Determine sua massa específica em $g/cm^3$, $kg/m^3$ e $kg/l$.
22.- Determine a massa de um bloco de chumbo que tem arestas de 10 cm, sendo que a massa específica do chumbo é igual 11,2 g/cm^{3}.
23. Um cubo maciço de alumínio cuja massa específica é $\mu_{Al} = 2,7\,g/cm^{3}$, de $a=50\,cm$ de aresta, está apoiado sobre uma superfície horizontal. Qual é a pressão, em $Pa$ e em $atm$, exercida pelo cubo sobre a
superfície?
24. (UFRJ) – O impacto de uma partícula de lixo que atingiu a nave espacial Columbia produziu uma pressão de $p=100\,N/cm^{2}$. Nessas condições e tendo a partícula $S=2 cm^{2}$, a nave sofreu uma força de:
( )a) $100\,N$;
( )b) $200\,N$;
( )c) $400\,N$;
( )d) $800\,N$;
( )e) $1600\,N$.
25. Um bloco de ferro ($\mu_{Fe}=7,6\,g/cm^{3}$) tem as seguintes dimensões: $20\,cm x 30\,cm x 15\,cm$. Determine:
a) A massa do bloco.
b) A maior e a menor pressão que este bloco poderá exercer sobre a mesa sobre a qual ele
será colocado, quando apoiado em uma das suas três faces. Dado: aceleração da gravidade $g=10\,m/s^{2}$.
26. (UNIPAC-97) A densidade do alumínio é $\mu=2,7\,g/cm^{3}$. Isso significa que um cubo maciço de
alumínio com aresta de $a = 0,8\,m$ terá massa aproximadamente de:
( )a) 19\,kg;
( )b) 1,4\, kg;
( )c) 1,9×10^{2}\,kg;
( )d) 1,4×10^{3}\,kg;
( )e) 19\,kg.
27.- Um reservatório contém água até uma altura de $h= 8,0\,m$. Determine a pressão hidrostática no fundo do reservatório. Dado: $g = 10\,m/s^{2}$, $\mu_{água} = 1000 kg/m^{3}$.
28.- O nível de água contida numa caixa fechada está $h =10\,m$ acima de uma torneira. Qual é a
pressão hidrostática sobre a torneira? Dado: $g = 10\,m/s^{2}$; $\mu_{água} = 1000\,kg/m^{3}$.
29.- Qual a pressão total (atmosférica + hidrostática) sobre um mergulhador que está a uma profundidade de $h =5\,m$? Dado: $g = 10\,m/s^{2}$; $\mu_{água} = 1000\,kg/m^{3}$.
30.- Uma piscina com $h =5\,m$ de profundidade está cheia com água. Considere $\mu_{água} = 1000\,kg/m^{3}$,
$g = 10\,m/s^{2}$, e $P_{atm}= 1,0\times {10}^{5}Pa$ determine:
a) a pressão hidrostática a $h =3,0\,m$ de profundidade;
b) a pressão absoluta no fundo da piscina;
c) a diferença de pressão entre dois pontos separados, verticalmente, por $\Delta h =80\,cm$.
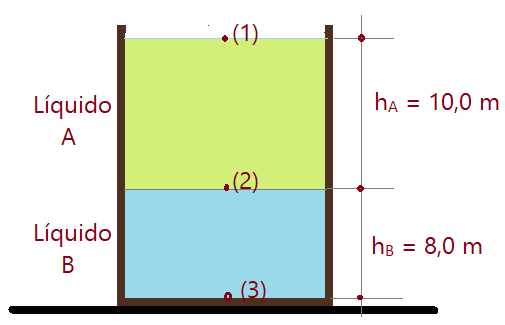
31.- Um grande reservatório aberto contém dois líquidos, A e B, cujas massas específicas são, respectivamente, $\mu_{A}=0,70\,g/cm^{3}$ e $\mu_{B} =1,5\,g/cm^{3}$ (veja a figura). A pressão atmosférica local é de $P_{at} = 1,0\times {10}^{5}\,N/m^{2}$. Qual é, em $N/m^{2}$, a pressão absoluta nos pontos (1), (2) e (3)? Dado: aceleração da gravidade $g=10\,m/s^{2}$.
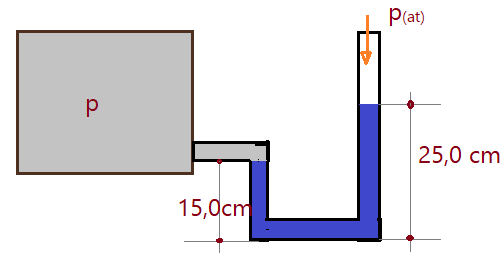
32.- (UFOP-93) Para se medir a pressão $P$ de um gás, usa-se um manômetro, que consiste de um tubo em forma de U contendo mercúrio cuja massa específica é $\mu_{Hg} = 13,6\times{10}^{3}\,kg/m^{3}$. Com base na figura, e sendo a pressão atmosférica $P_{at}=1,0×10^{5}\,N/m^{2}$, determine o valor de $P$ na unidade $Pa$. Considere a aceleração da gravidade local $g=10\,m/s^{2}$.
33. Num posto de gasolina, para a lavagem de um automóvel de massa $m =1000\,kg$, o mesmo é
erguido a certa altura. O sistema utilizado é uma prensa hidráulica. Sendo os êmbolos de áreas $S_{1}=10\,cm^{2}$ e $S_{2} = 2000\,cm^{2}$ e a aceleração da gravidade local é de $g = 10\,m/s^{2}$, pergunta-se:
a) em qual êmbolo deve-se apoiar o carro?
b) em qual êmbolo deve-se pressionar para se sustentar o carro?
c) qual a força aplicada no êmbolo para equilibrar o automóvel?
34.- Um mecânico equilibra um automóvel, usando um elevador hidráulico. O automóvel pesa $P = 800\,kgf$, equivalentes a$ 8000\\,N$ e está apoiado em um pistão cuja área é de $S_{2}=2.000\,cm^{2}$. Determine o valor da força que o mecânico está exercendo na chave, sabendo-se que a área do pistão no qual ele atua é de $S_{1}= 25,0\,cm^{2}$.
35. (Direito.C.L.-94) Um corpo pesa $P=4\,N$ fora da água. Imerso totalmente em água o seu peso aparente é $P_{a}=3\,N$. O empuxo exercido pela água sobre o corpo é de :
( )a) $7,0\,N$;
( )b) $12,0\,N$;
( )c) $3,0\,N$;
( )d)$1,0\,N$;
( )e) $4,0\,N$.
36.- (UFV 94) Sabe-se que certos peixes possuem certa estrutura denominada bexiga natatória, que tem por finalidade lhes permitir permanecerem imersos a certa profundidade. A função física da bexiga natatória é controlar a densidade média do peixe de forma a:
a) alterar a densidade da água;
b) manter o empuxo menor que seu peso;
c) manter o empuxo maior que seu peso;
d) manter o empuxo igual que seu peso;
e) alterar a sua massa.
37. (UFLA-95) O empuxo exercido sobre um corpo imerso em um líquido depende:
a) do volume do líquido deslocado e da densidade do corpo;
b) da densidade e do volume do corpo;
c) do volume e da densidade do líquido deslocado;
d) somente do volume do líquido deslocado;
e) somente da densidade do líquido deslocado.
38.- (Direito.C.L.- 96) O princípio de Arquimedes trata das forças que atuam num corpo quando
colocado num fluido qualquer. Este princípio está relacionado com os fatos apresentados nas
afirmações abaixo EXCETO:
a) Se afundarmos um balão de plástico numa piscina, quando o soltarmos, ele subirá até a superfície e flutuará;
b) Se enchermos um balão de plástico com um gás especial ele poderá flutuar no ar, enquanto se ele for cheio com gás de nossos pulmões, observaremos que ele não flutuará
e cairá no chão;
c) Na linguagem comum, costumamos dizer que os aviões são aparelhos mais pesados que o ar, indicando que o empuxo que recebem do ar é menor do que seu peso;
d) é impossível fazer um balão cheio de gás flutuar na lua;
e) o peso de um balão na lua, é menor do que o peso de um balão na Terra.
Bom êxito na resolução dos exercícios. Se tiver dificuldades, consulte-me por um dos canais abaixo listados.
Curitiba, 02 de agosto de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
