FI.ME.016-01 – Física, Mecânica. Hidrostática, fluidos em equilíbrio.
Fluido
Denominamos fluidos a todos as porções de matéria que se encontram no estado líquido ou gasoso.
Fluidos em equilíbrio estático
Um fluido está em equilíbrio estático quando não existem movimentações de suas partículas na forma de correntes de fluxo. Neste caso temos o estado do fluido caracterizado pelas grandezas volume, pressão e temperatura. O volume e a forma dependem do recipiente em que está contido.
Pressão
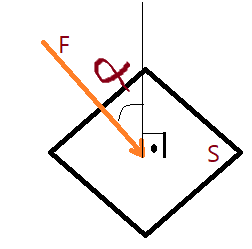
Se exercemos uma força $\color{Maroon}{\vec{F}}$, sobre uma superfície na direção normal a esta, a ação da força de distribui em todos os pontos dessa superfície, de modo uniforme. Daí a necessidade de definirmos uma grandeza conveniente para traduzir a intensidade da força por unidade de área dessa superfície.
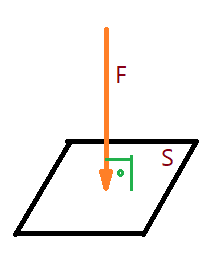
A força aplicada sobre a superfície, exerce sobre esta uma pressão.
Pressão da força $\vec{F}$ sobre a superfície $S$ é igual ao quociente da intensidade da força pela área da superfície.
$$\color{Maroon}{p = \frac{F}{S}}$$
Na figura em que a força atua numa direção oblíqua $\alpha$, recorremos ao cálculo da componente ortogonal à superfície.
$$\color{Maroon}{p = \frac{F\times cos\alpha}{S}}$$
Nota: É possível que alguém pergunte qual o motivo de o ângulo de ação da força ser medido em relação à reta normal e não em relação à superfície. É bem simples entender a razão. A superfície nem sempre será plana e não é possível estabelecer ângulos trigonométricos em relação à uma curva. Por isso sempre tomamos a reta normal por referência. A reta normal é perpendicular à tangente no ponto considerado.
As unidades de pressão são derivadas das unidades das duas grandezas.
No sistema internacional de unidades temos:
$p = N/m^2 = pascal (Pa)$
No sistema CGS, temos:
$p = dyn/cm^2 $
No sistema técnico ou MKgfS:
$p = kgf/m^{2}$
Existe uma unidade prática que é o valor de uma vez a pressão atmosférica ao nível do mar, na temperatura próxima de $0^0C$.
$1\,atm = 101.325\,Pa$
$1\,Pa = 10\,dyn/cm^2$
Exemplo 1. Uma força de intensidade $\color{Maroon}{F =30,0\,N}$ é aplicada perpendicularmente à superfície de um bloco cuja área é $\color{Maroon}{S = 0,30\,m^2}$, qual a pressão exercida por esta força?
Dados: $F = 30,0\,N$ e $S = 0,30\,m^2$.
$$\color{Brown}{p = \frac{F}{S}}$$
$p = \frac{30,0}{0,30} = 100,0\,Pa$
$$\color{Navy}{p = 100,0\,Pa}$$
Exemplo 2. Uma superfície de $\color{Sepia}{S = 2,75\,m^{2}}$, suporta uma pressão uniforme de $\color{Sepia}{p = 320,0\,Pa}$. Determine a intensidade da força total recebida pela superfície.
Dados: $S = 2,75\,m^{2}$ e $p=320,0\,Pa$
$$\color{Maroon}{p = \frac{F}{S}}$$
$F = p\times S$$\Leftrightarrow$$ F = 320,0\times 2,75 = 880,0\,N$
Superfície recebe uma carga de: $$\color{Navy}{F=880,0\,N}$$
Exemplo 3. Uma força de $\color{Sepia}{F= 3,4\times 10^{7}\,dyn}$ atua sobre uma superfície de $\color{Sepia}{S = 1,7\times 10^{2}\,cm^{2}}$, num ângulo de $\color{Sepia}{\alpha = 45^{0}}$ em relação à reta normal no ponto de ação. Se a superfície é plana, qual é a pressão sobre a superfície, se a força for uniformemente distribuida?
$$\color{Maroon}{p = \frac{F\times cos\alpha}{S}}$$
$p = \frac{3,4\times 10^{7}\times cos(45^{0})}{1,7\times 10^{2}}$$\Leftrightarrow$$ p = \frac{3,4\times 10^{7}\times \frac{\sqrt{2}}{2}}{1,7\times 10^{2}}$
$p = \frac{1,7\times 10^{7}\times\sqrt{2}}{1,7\times 10^{2}}$
$p = 10^{5}\times\sqrt{2} = 1,41\times 10^{5}\,dyn/cm^{2}$
A pressão na superfície será de:$$\color{Navy}{p = 1,41\times 10^{5}\,dyn/cm^{2}}$$
Exemplo 4. Determine a área da superfície que suporta uma pressão de $\color{Sepia}{p = 7,2\times 10^{3}\,kgf/m^{2}}$, produzida por uma força de $\color{Sepia}{F = 360\,kgf}$.
$$\color{Maroon}{p = \frac{F}{S}}$$
$S = \frac{360,0}{7,2\times 10^{3}} = 50\times 10^{-3}\,m^{2}$
A superfície tem área de: $$\color{Navy}{S = 5,0\times 10^{-2}\,m^{2}}$$
Pressão hidrostática
A pressão que um fluido em equilíbrio exerce sobre a superfície do recipiente, é denominada pressão hidrostática. Cabe notar que a direção da pressão é sempre normal à superfície, o que implica que a força resultante também terá essa característica.
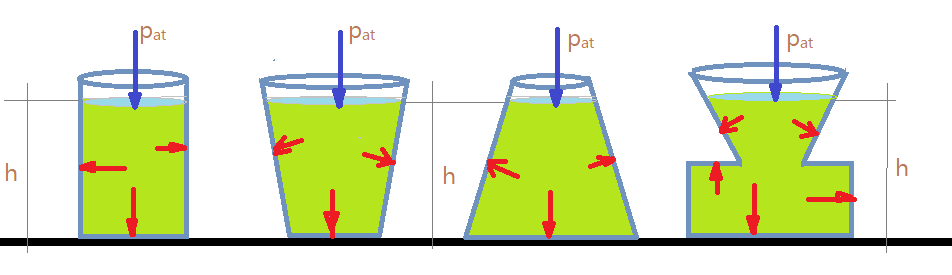
Podemos observar que o líquido em equilíbrio em diferentes recipientes, exerce pressão sempre normal à superfície interna do recipiente em cada ponto.
A pressão sobre o fundo do primeiro recipiente pode ser determinada, dividindo a força peso do líquido pela área da superfície.
$p_{f} = \frac{P}{S}$$\Leftrightarrow$$ p_{f}= \frac{m\times g}{S}$
Sabemos que a massa pode ser obtida pela multiplicação da massa específica(densidade) do líquido pelo volume.
$m = \mu\times V$$\Leftrightarrow$$m = \mu\times {S\times h}$
Substituindo na fórmula da pressão, teremos:
$p_{f} = \frac{\mu\times S\times h\times g}{S}$
Cancelando o fator comum $S$, teremos:
$$\color{Navy}{p_{f} = \mu\times g\times h}$$
Obs.: Note que a pressão que o líquido exerce sobre o fundo do recipiente, depende da massa específica, da aceleração da gravidade no local e da altura da coluna líquida no recipiente. A área do fundo não influi. Essa equação também serve para determinar a pressão em qualquer ponto no interior do recipiente, desde que conheçamos a sua profundidade em relação à superfície livre.
Então podemos afirmar que a pressão no fundo dos diferentes recipientes da figura, não depende da área dessa superfície. Estando todos com o mesmo líquido até a mesma altura, as pressões são iguais.
Se tivermos um recipiente, provido de tampa, mas com furos em diferentes pontos e alturas. Enchendo-o de água e mantendo-o tampado, não haverá vazamento, por causa da pressão atmosférica externa que é maior que a pressão da coluna de água, sendo ela menor do que 10,0 m. Vejamos a figura a seguir.
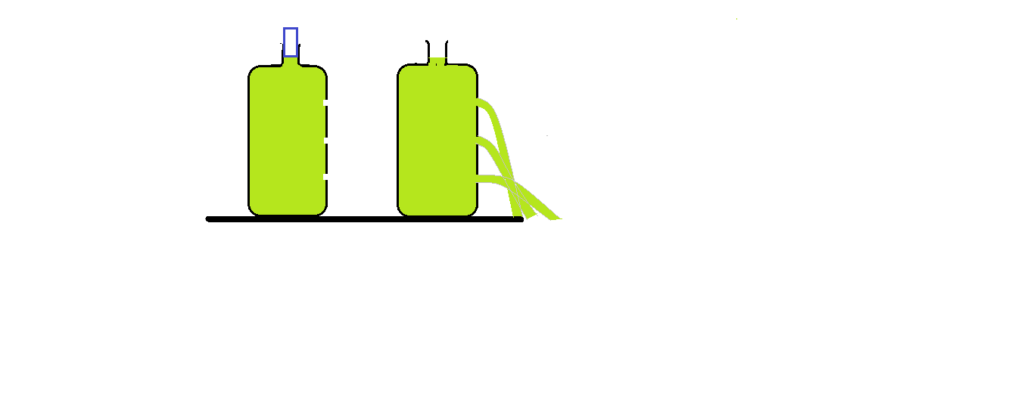


Pressão total ou absoluta:
Vemos na figura indicada a ação da pressão atmosférica sobre a superfície dos líquidos. Dessa forma, a pressão total ou absoluta no fundo ou mesmo em qualquer outro ponto no interior do líquido, é a soma da pressão da coluna líquida, com a pressão atmosférica, que é integralmente transmitida, sendo o líquido do tipo ideal.
$$\color{Maroon}{p = p_{at} + \mu g h}$$
Um líquido é ideal ou perfeito se for incompressível e desprovido de viscosidade. Já vimos em outros momentos que o conceito de algo ideal ou perfeito serve apenas como parâmetro para fins didáticos e de pesquisa. As variáveis de estado tem limites estabelecidos levando em consideração esse ideal. Poderíamos dizer que estabelece uma espécie de fronteira entre o que é possível e o que é impossível.
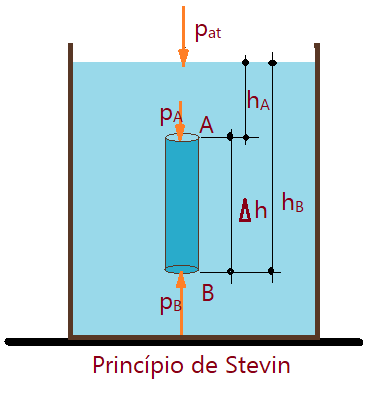
Princípio de Stevin ou Princípio Fundamental da Hidrostática.
Observando a figura notamos um cilindro, cuja superfície das bases consideraremos iguais à unidade e é de mesma densidade do líquido. Vamos estabelecer a pressão na base A e na base B, para depois obtermos a diferença entre estas pressões. Isso nos dará o Princípio de Stevin ou Princípio Fundamental da Hidrostática.
$ p_{A} = p_{at} + \mu g h_{A}$ ( I)
$ p_{B} = p_{at} + \mu g h_{B}$ (II)
$\Delta p = p_{B} – p_{A}$$\Leftrightarrow$$\Delta p = {(p_{at} + \mu g h_{B})} – {(p_{at} + \mu g h_{A})}$
$\Delta p =\not{p_{at}} + \mu g h_{B} – \not{p_{at}} – \mu g h_{A}$$\Leftrightarrow$$\Delta p = \mu g{(h_{B} – h_{A})}$
$$\color{Navy}{\Delta p = \mu g\Delta h}$$
Enunciado do princípio:
“A diferença de pressão entre dois pontos situados em níveis diferentes no interior de um líquido perfeito em equilíbrio é igual ao produto da massa específica pela aceleração da gravidade e a diferença de nível”.
Consequências:
- Dois pontos situados no mesmo nível em um líquido em equilíbrio suportam pressões iguais.
- A superfície livre de um líquido em equilíbrio, suporta a mesma pressão em todos os pontos, e consequentemente é horizontal.
- Como já vimos no nosso raciocínio a pressão aumenta com o aumento da profundidade do ponto considerado.
Teorema de Pascal
“A pressão exercida sobre um líquido perfeito é transmitida integralmente ao longo de todos os pontos do mesmo.”
É esse conceito que nos leva a somar a pressão atmosférica à pressão da coluna líquida para determinar a pressão em um ponto qualquer no interior do líquido em equilíbrio.
Prensa hidráulica
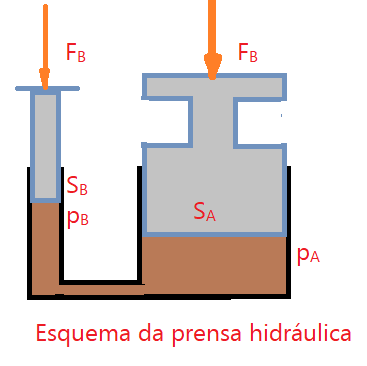
É provavelmente a aplicação mais importante do Teorema de Pascal. A prensa hidráulica é constituída basicamente de dois cilindros, providos de êmbolos, cheios de um óleo que lubrifica e não corrói. Esquematicamente é o que mostramos na figura que segue. O uso do óleo para transmitir a pressão tem a vantagem de ser pouco viscoso.
Observe que no esquema temos dois pistões, sendo um de área $S_{B}$ e outro de área $S_{A}$, estão em contato com um óleo contido no sistema. As pressões nos dois êmbolos são iguais e isso permite fazer esta deducção.
$$\color{Maroon}{p_{B} = p_{A}}$$
Substituindo pela expressão $p = \frac{F}{S}$
$\color{Navy}{\frac{F_{B}}{S_{B}} = \frac{F_{A}}{S_{A}}}$
Sendo os pistões de forma cilíndrica, as áreas de suas secções transversais são:
$$\color{Maroon}{S = \pi R^2 = \pi\frac{D^2}{4}}$$
$\frac{F_{B}}{\not{\pi} R_{B}^2} = \frac{F_{A}}{\not{\pi} R_{A}^2}$
$$\color{Navy}{\frac{F_{B}}{R_{B}^2} = \frac{F_{A}}{R_{A}^2}}$$
$\frac{F_{B}}{\not{\pi}\frac{D_{B}^2}{\not{4}}} = \frac{F_{A}}{\not{\pi}\frac{D_{A}^2}{\not{4}}}$
$$\color{Navy}{\frac{F_{B}}{D_{B}^2} = \frac{F_{A}}{D_{A}^2}}$$
Numa prensa hidráulica ocorre conservação do trabalho mecânico. Não há atrito, não há eixos, engrenagens, correias ou polias de transmissão. O que ganhamos em força, perdemos em deslocamento. Por isso as aplicações práticas são providas de um sistema compressor que bombeia o óleo hidráulico para dentro do pistão de maior diâmetro. Os macacos hidráulicos tem no êmbolo menor uma alavanca acionadora, reduzindo a intensidade da força necessária para levantar objetos de peso avantajado.
Se fôssemos listar todas as formas de aplicação dos sistemas de prensa hidráulica, iríamos encher um volume razoável. Vamos citar alguns mais comuns. Em nossos automóveis temos o freio hidráulico com o sistema de “servo-freio”, ligado ao motor do veículo; os denominados “macaco hidráulico” para elevar os automóveis na troca de rodas, efetuar reparos. Nos equipamentos de terraplanagem os comandos de mover as pás, elevar, baixar são todos feitos por meio de sistemas hidráulicos. É inimaginável a variedade de aplicações.
Exercitando:
01. Determine a diferença de pressão entre dois pontos localizados a $10\,m$ e a $20\,m$ de profundidade em um lago de águas salobras com densidade igual a $1200 kg/m^3$. Consideremos $g = 10,0\,m/s^2$.
Pelo Princípio de Stevin, temos:
$$\color{Navy}{\Delta p = \mu g \Delta h}$$
$\Delta p = 1200\times 10\times {(20 – 10)}$$\Leftrightarrow$$\Delta p = 12000\times 10 = 120.000\,Pa$
$$\color{Navy}{\Delta p = 1,2\times{10}^5}\,Pa$$
02. Um macaco hidráulico tem o pistão maior com diâmetro de $12\,cm$ e o menor, com diâmetro de $2,5\,cm$. Determine a carga que conseguiremos elevar com esse macaco, aplicando uma força de $F_{B}= 120,0\,N$. Qual é o volume do líquido deslocado para o pistão maior, até ele se elevar de $h=25\,cm$.
Dados: $D_{A}= 12,0\,cm$, $D_{B} = 2,5\,cm$, $F_{B} = 120,0\,N$ e $h_{A}=25\,cm$.
$\frac{F_{B}}{D_{B}^2} = \frac{F_{A}}{D_{A}^2}$$\Leftrightarrow$$ \frac{120,0}{(2,5)^2} = \frac{F_{A}}{(12,0)^2}$
$\frac{120,0}{6,25} = \frac{F_{A}}{144,0}$$\Leftrightarrow$$19,2\times 144 = F_{A}$
$$\color{Navy}{F_{A} = 2.764,8\,N}$$
$V_{A} = {\frac{\pi\times D^4}{4}}\times{25}$$\Leftrightarrow$$V_{A} = {\frac{\pi\times
{12}^2}{4}}\times{25} = 2.827,43\,cm^3$
$$\color{Navy}{V_{A} = 2.827,43\,cm^3}$$
Vasos comunicantes
Denominamos vasos comunicantes a dois ou mais recipientes, interligados pela base e contendo um determinado líquido.
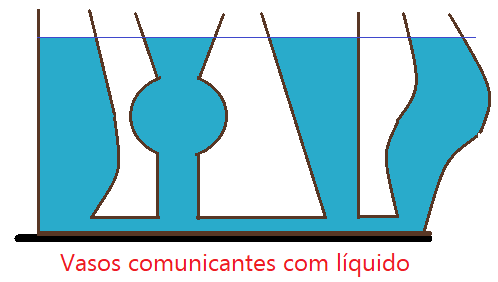
Um mesmo líquido, colocado em vasos comunicantes, atinge a mesma altura em todos os seus ramos. Veja a ilustração que segue.
Equilíbrio de líquidos imiscíveis em vasos comunicantes.
O caso mais comum de vasos comunicantes é o dos vasos em forma de U.
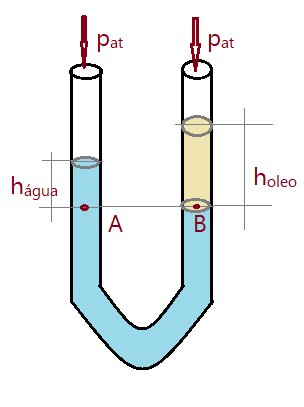
Imaginemos um vaso em forma de U, contendo água e sobre a água em um dos ramos colocamos uma porção de óleo. A densidade da água é próxima de $\delta = 1$ e o óleo tem densidade menor $\delta < 1$. Analisaremos o equilíbrio desses dois líquidos no tubo. Veja a ilustração.
Os pontos A e B estão no mesmo nível do líquido mais denso (água) e nos dois tubos atua a pressão atmosférica sobre a superfície dos líquidos.
$$\color{Maroon}{p_{A} = p_{B}}$$
No ramo A temos uma porção de água de altura $h_{água}$ e no ramo B, acima do ponto B, temos óleo até uma altura $h_{óleo}$. A água tem massa específica $\mu_{água}$ e o óleo $\mu_{óleo}$.
$p_{at} + \mu_{água} g h_{água} = p_{at} + \mu_{óleo} g h_{óleo}$
Cancelando os termos semelhantes simétricos e os fatores comuns, temos:
$$\color{Navy}{\mu_{água} h_{água} = \mu_{óleo} h_{óleo}}$$
Exemplo 1. Em um tubo na forma de U, temos uma certa quantidade de mercúrio ($\mu_{Hg}=13,6\,g/cm^3$), que se estabiliza tendo as superfícies livres no mesmo nível. Coloca-se em um dos ramos uma coluna de água igual a $h_{H_{2}0}= 30\, cm$ e depois uma coluna de óleo de $h_{óleo}= 15\,cm$. Sendo a massa específica da água $\mu_{H_{2}O} = 1\,g/cm^3$ e do óleo $\mu_{óleo}= 0,82\,g/cm^3$, determinar o desnível produzido nas superfícies do mercúrio nos dois ramos do tupo.
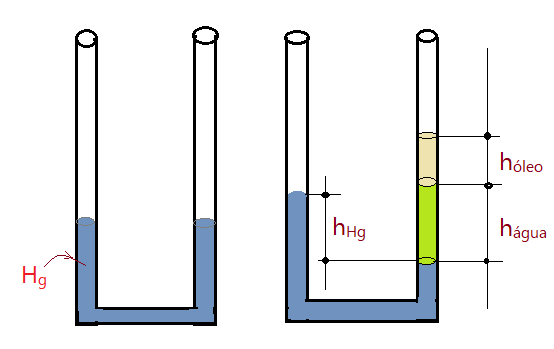
Nestes exercícios é sempre conveniente desenhar o tubo indicando as alturas e níveis dos líquidos, para então aplicar o Princípio de Stevin na situação de equilíbrio.
Os pontos de nível mais baixo com a mesma pressão, podemos considerar o nível da superfície de separação entre o mercúrio e a água. Vamos denominar estes pontos de A e B. Assim:
$$\color{Maroon}{p_{A} = p_{B}}$$
$\not{p_{at}} + \mu_{Hg}\not{g}h_{Hg} = \not{p_{at}} + \mu_{H_{2}O}\not{g} h_{H_{2}O} + \mu_{óleo}\not{g}h_{óleo}$
Cancelamos os termos simétricos da pressão atmosférica e os fatores comuns $g$.
$ \mu_{Hg} h_{Hg} = \mu_{H_{2}O} h_{H_{2}O} + \mu_{óleo} h_{óleo}$
${13,6}\times h_{Hg} = 1\times {25} + 0,82\times {15}$$\Leftrightarrow$$h_{Hg} = \frac{25 + 12,3}{13,6}$
$$\color{Navy}{p_{Hg} = \frac{37,3}{13,6} = 2,74\,cm}$$
O mercúrio sofrerá um desnível de $2,74\,cm$.
Exemplo 2. Se um par de vasos comunicantes cilíndricos tem as áreas da secção reta $S_{A} = 10,0\,cm^2$ e $S_{B}=6,0\,cm^2$. Se temos água pura em equilíbrio nos vasos e depois introduzimos no ramo mais estreito $V_{óleo}=90,0\,cm^3$, qual é o desnível da água nos dois ramos? Qual é o volume de água que fica acima da superfície de separação dos dois líquidos no no outro ramo? Dado: $\mu_{óleo}=0,78\,g/cm^3$.
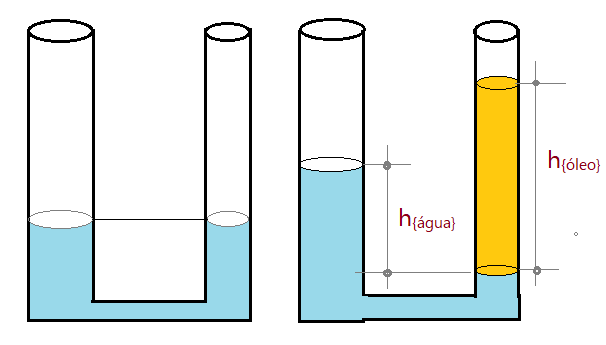
Vejamos a figura.
Primeiro vemos a água em equilíbrio nos dois ramos dos vasos comunicantes. Na segunda parte da figura vemos a coluna de óleo sobre a água, deslocando a mesma até um nível diferente por causa da pressão resultante do peso do óleo.
Primeiramente precisamos determinar a altura da coluna de óleo, pois o problema nos fornece o volume e a massa específica junto com a área da secção reta do ramo.
Volume de um cilindro é: $V = S_{b}\times h_{óleo}$
$90,0 = 6,0\times h_{óleo}$$\Leftrightarrow$$h_{óleo}= \frac{90,0}{6,0} = 15,0 cm$
Agora podemos aplicar o Princípio de Stevin.
$\mu_{H_{2}O} h_{H_{2}O} = \mu_{óleo} h_{óleo}$$\Leftrightarrow$$1\times h_{H_{2}O} = {0,78}\times {15,0}$
$\color{Navy}{$h_{H_{2}O} = 11,7\,cm}$$
O desnível entre as superfícies da água é de $h_{H_{2}O}=11,7\,cm$.
Como o desnível da água está no ramo mais largo, o volume é diferente.
$$\color{Maroon}{V_{H_{2}O} = S_{b}\times h_{H_{2}O}}$$
$V_{H_{2}O} = 10,0\times 11,7$$\Leftrightarrow$$V_{H_{2}O}=117,0\,cm^3$
O volume de água deslocada é igual a $V_{H_{2}O}= 117,0\,cm^3$
Exemplo 3. Um elevador hidráulico é constituído por um pistão de diâmetro $D_{E} = 35,0\,cm$. Para elevar um automóvel de $m= 1500,0\,kg$, até uma altura $h = 2,0\,m$, qual é a pressão necessária na base do cilindro e qual o volume de óleo bombeado pelo compressor para essa elevação? Considere $g= 10,0\,m/s^2$.
O peso do automóvel é: $P_{a}= m\times g = 1500,0\times 10 = 15000,0\,N$
$p = \frac{P}{S} = \frac{15000,0}{\frac{\pi D^2}{4}}$$\Leftrightarrow$$p = \frac{15000,0}{\frac{\pi {0,35}^2}{4}}$
$$\color{Navy}{p = \frac{15000,0}{0,096} = 156250,0\,Pa}$$
O volume de óleo bombeado será dado pelo volume do cilindro.
$$\color{Maroon}{V = \pi D^{2} h}$$
$V = \pi {0,35}^{2}\times 2,0\simeq 0,7697\,m^{3}$
$$\color{Navy}{V \simeq 0,7697\,m^3}$$
Medindo a pressão
O aparelho para medir a pressão é denominado manômetro. Existe uma grande variedade de manômetros.
Manômetro de líquido
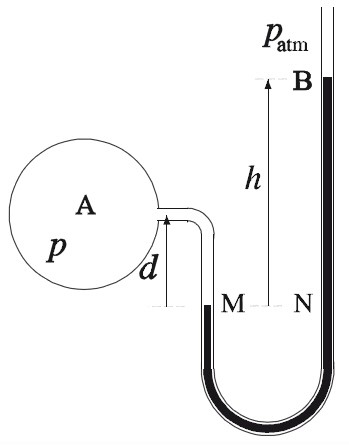
É constituído de um tubo com forma de U, de secção uniforme, tendo uma escala indicativa da pressão num dos ramos que é mais alto. Nesse tipo de manômetro habitualmente usa-se mercúrio, por ter uma massa específica mais elevada. Para usar água ou outro líquido a coluna de líquido teria uma altura impraticável.
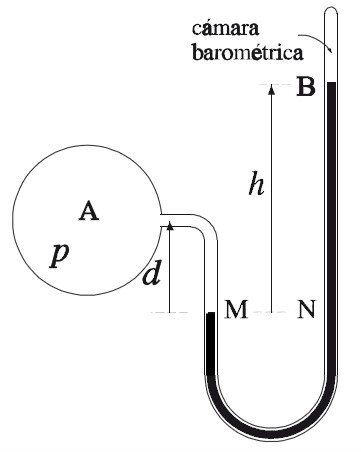
Também há o manômetro truncado, onde o ramo que receberia a pressão atmosférica é fechado, formando uma câmara barométrica. Ele mede a pressão denominada manométrica.
Manômetro metálico ou aneróide.


Os manômetros mais usados, especialmente em pressões mais elevadas, são os metálicos. Um tubo metálico laminado é enrolado em forma de anel ou espiral. Ao ser submetido à uma variação de pressão o tubo tende a modificar o grau de enrolamento. A extremidade livre aciona um dispositivo amplificador, ligado a um ponteiro. Esse ponteiro gira sobre um eixo e sua extremidade mostra a pressão na escala do aparelho.
Há diversos tipos de manômetros, como o de membrana. Uma membrana elástica, sofre deformação causada pela pressão e aciona um dispositivo registrador, indicando a pressão.
Manômetros especiais
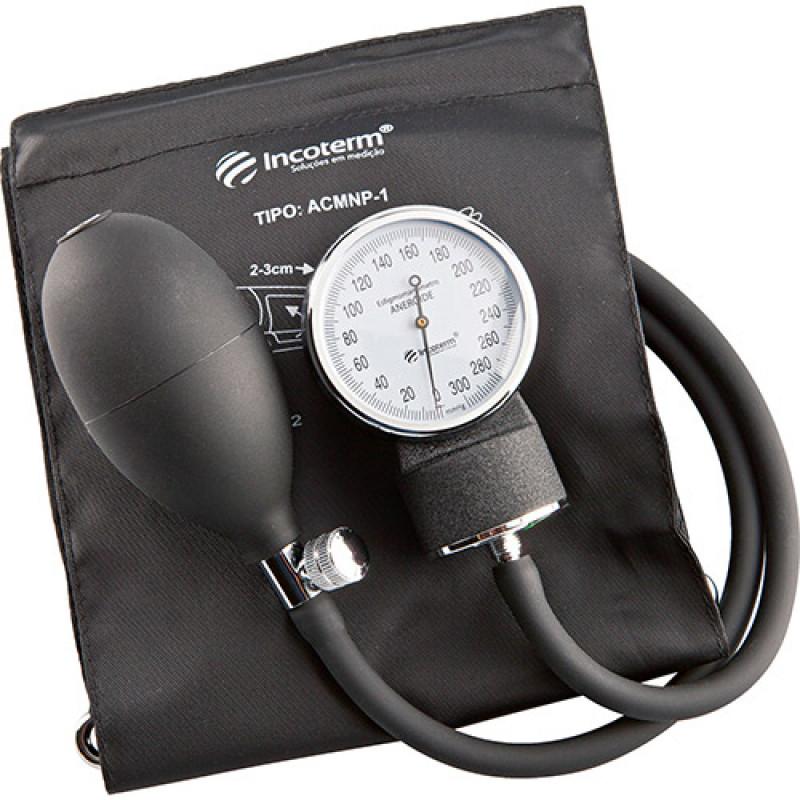
- Esfigmomanômetro é usado por um médico ou outra pessoa ligada à área da saúde para aferir a pressão arterial de uma pessoa. O procedimento combina o manômetro com um estetoscópio.
- Barômetro é destinado à medir a pressão atmosférica. Entre os mais conhecidos está o Barômetro de Torricelli.
Evangelista Torricelli, matemático e físico italiano, na busca de provar a existência e também uma forma de medir a pressão atmosférica, tomou um tubo de vidro, com aproximadamente um metro de comprimento, fechado em uma extremidade. Encheu-o de mercúrio. Em um recipiente mais amplo colocou mercúrio. Tampou com o dedo a extremidade do tubo, inverteu sua posição, mergulhando a extremidade no mercúrio do recipiente. Retirando o dedo, observou que o mercúrio, sem deixar entrar ar, desceu até uma altura de $h = 76\,cm$. Assim ele tinha a prova da existência da pressão atmosférica e também podia medir seu valor. Bastava calcular a pressão da coluna de mercúrio que ficou em equilíbrio. Vejamos a figura.
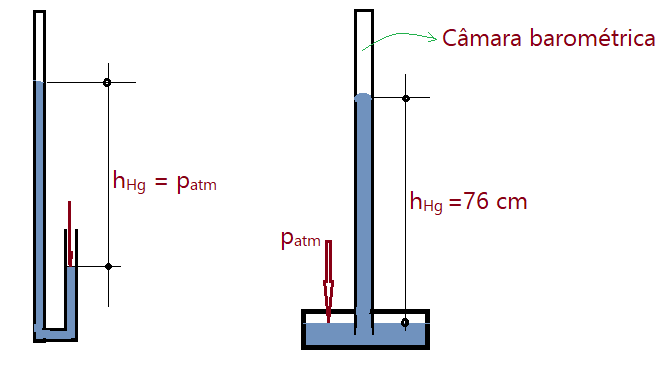
A figura da direita reproduz como Torricelli procedeu para provar a pressão atmosférica e ao mesmo tempo estabelecer uma forma de medi-la.
A figura da esquerda traz a forma simplificada do barômetro, que ficou mais prático de manusear, é menos tóxico por conta da redução de evaporação, pois a área da superfície livre é pequena. Além disso economiza mercúrio. A câmara barométrica existente acima do mercúrio no lado fechado do tubo, é um vácuo parcial. Existe ali uma tênue quantidade de vapor de mercúrio.
Há também os barômetros aneróides, utilizados em situações apropriadas.
A pressão atmosférica considerada normal é aquela que medimos ao nível do mar. Podemos determinar o valor, aplicando o Princípio de Stevin.
$\color{Maroon}{p_{at}= \mu_{Hg}\times g\times h}$$
$p_{at} = 13,65\times 9,81\times 0,76$$\Leftrightarrow$$p_{at}= 101.396\,Pa$
$$\color{Navy}{p_{at}= 101396\,Pa}$$
Obs.: Na medida que subimos para as camadas mais elevadas da atmosfera, a pressão atmosférica diminui devido à rarefação do ar. Isso é causado por conta da redução que ocorre na aceleração da gravidade e a consequente fuga de moléculas gasosas para o espaço. A espessura e consequente densidade do ar que circunda o globo depende do valor da gravidade, que atrai as partículas gasosas, mantendo-as literalmente presas ao seu redor.
Exercícios para resolver.
01. (UNIPAC) – Uma prensa hidráulica possui pistões com diâmetros $D_{1}= 10\,cm$ e $D_{2} =20\,cm$. Se uma força de $F_{1}=120\,N$ atua sobre o pistão menor, pode-se afirmar que esta prensa estará em equilíbrio quando sobre o pistão maior atuar uma força de:
( )a) 30 N;
( )b) 60 N;
( )c) 480 N;
( )d) 240 N;
( )e) 120 N.
02. (PUC-RS) – No oceano a pressão hidrostática aumenta aproximadamente uma atmosfera a cada 10 m de profundidade. Um submarino encontra-se a 200 m de profundidade, e a pressão do ar no seu interior é de uma atmosfera. Nesse contexto, pode-se concluir que a diferença da pressão entre o interior e o exterior do submarino é, aproximadamente, de
( )a) 200 atm;
( )b) 100 atm;
( )c) 21 atm;
( )d) 20 atm;
( )e) 19 atm.
03. (Fei) – No macaco hidráulico representado na figura a seguir, sabe-se que as áreas das secções transversais dos vasos verticais são $A_{1} = 20\,cm^2$ e $A_{2} = 0,04\,m^2$. Qual é o peso máximo que o macaco pode levantar, quando fazemos uma força de $F_{1}= 50,0\,N$ em $A_{1}$?
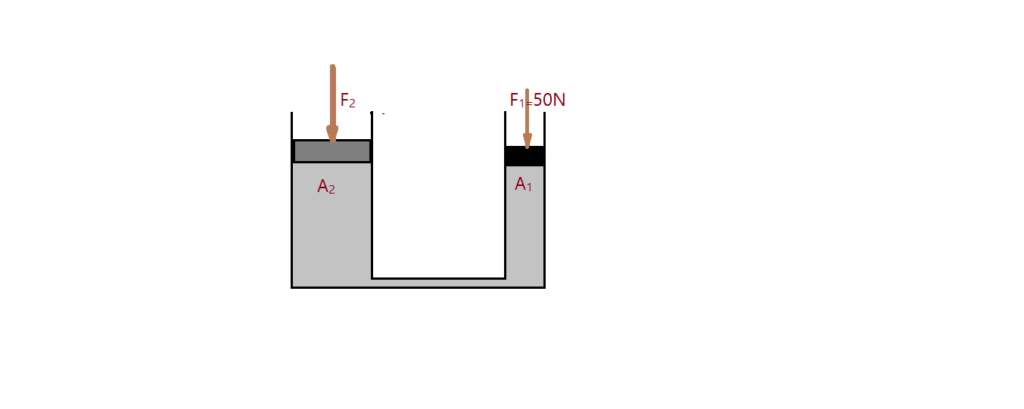
( )a) 100 N;
( )b) 1000 kgf;
( )c) 1000 N;
( )d) 10000 kgf;
( )e) 200 kgf.
04. (Fgv) – O macaco hidráulico consta de dois êmbolos: um estreito, que comprime o óleo, e outro largo, que suspende a carga. Um sistema de válvulas permite que uma nova quantidade de óleo entre no mecanismo sem que haja retorno do óleo já comprimido. Para multiplicar a força empregada, uma alavanca é conectada ao corpo do macaco.
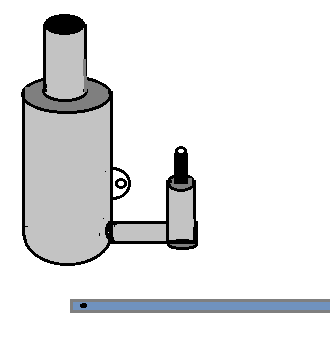
Tendo perdido a alavanca do macaco, um caminhoneiro de massa $m_{1}=80\,kg$, usando seu peso para pressionar o êmbolo pequeno com o pé, considerando que o sistema de válvulas não interfira significativamente sobre a pressurização do óleo, poderá suspender uma carga máxima, em kg, de Dados:
diâmetro do êmbolo menor $D_{1} = 1,0\,cm$
diâmetro do êmbolo maior $D_{2}= 6,0\.cm$
aceleração da gravidade $g = 10\,m/s^2$
( )a) 2 880;
( )b) 2 960;
( )c) 2 990;
( )d) 3 320;
( )e) 3 510.
05. (Ufrgs) – Assinale a alternativa que preenche corretamente as lacunas do texto que segue, na ordem em que aparecem. A figura a seguir representa uma prensa hidráulica composta por dois pistões, de diâmetros $d_{1}$ e $d_{2}$. O motor aplica uma força axial de intensidade $F_{1} = 100\,N$ no pistão de diâmetro$d_{1} = 0,05\,m$. Para que se possa obter uma força de intensidade $F_{2} = 10000\,N$ no pistão de diâmetro d_{2}, esse diâmetro deve ser igual a ___________, e a pressão transmitida será de ____________.
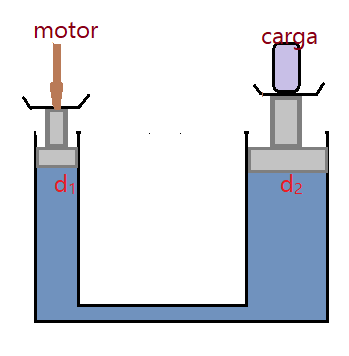
( )a) 0,25 m; 50,9 kPa;
( )b) 0,50 m; 12,7 kPa;
( )c) 0,50 m; 50,9 kPa;
( )d) 0,12 m; 50,9 Pa;
( )e) 0,12 m; 12,7 Pa.
06. (Ufsm) – Ao ser medicado, um jogador recebeu uma injeção com uma seringa cujo êmbolo tem secção reta de $S_{2}=1,2\,cm^2$. O médico, ao aplicar o medicamento, exerceu, sobre o êmbolo, uma força com módulo de $F_{2}=6,0\,N$. A elevação, em $N/m^2$ da pressão produzida na ponta da agulha, cuja secção reta tem uma área de $S_{1}= 0,01\,cm^{2}$, é:
( )a) 6 × 10^{6};
( )b) 5 × 10^{4};
( )c) 720;
( )d) 6;
( )e) 5 × 10^{-2}.
07. (Fuvest) – Considere o arranjo da figura a seguir, onde um líquido está confinado na região delimitada pelos êmbolos A e B, de áreas $S_{A} = 80\, cm^2$ e $S_{B} = 20\,cm^2$, respectivamente.
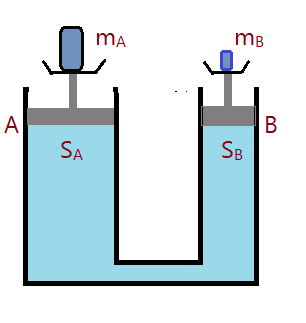
O sistema está em equilíbrio. Despreze os pesos dos êmbolos e os atritos. Se $m_{A} = 4,0\,k$g, qual o valor de $m_{B}$?
( )a) 4 kg;
( )b) 8 kg;
( )c) 16 kg;
( )d) 2 kg;
( )e) 1 kg.
08. (Uncisal) – Em um laboratório, as substâncias são identificadas no rótulo pelo nome e por algumas propriedades químicas. No intuito de descobrir qual a substância armazenada num frasco no qual o rótulo foi retirado, um estudante aplicado de física propôs um experimento. Foram colocados num sistema constituído por vasos comunicantes o líquido desconhecido e álcool. Como são líquidos imiscíveis, é possível estimar a densidade do líquido medindo a altura das colunas líquidas a partir da superfície de separação desses líquidos. Esses valores são mostrados na figura a seguir. Consultando a tabela com os valores das densidades de alguns líquidos, disponível nesse laboratório, é provável que o líquido desconhecido seja:
| Líquido | $\mu=g/cm^3$ |
| Álcool | 0,79 |
| Benzeno | 0,90 |
| Água | 1,00 |
| Mercúrio | 13,60 |
| Hexano | 0,66 |
| Nitroglicerina | 1,60 |
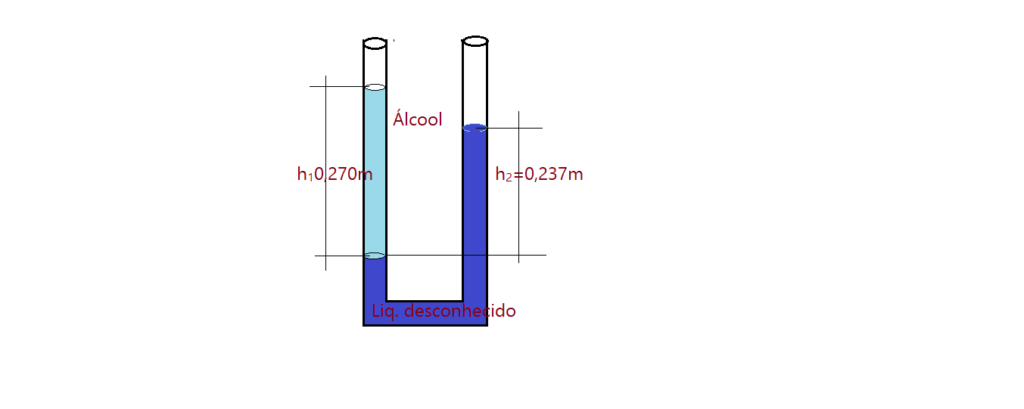
( )a) a nitroglicerina;
( )b) o hexano;
( )c) o mercúrio;
( )d) a água;
( )e) o benzeno.
09. (Unifesp) – O sistema de vasos comunicantes da figura contém água em repouso e simula uma situação que costuma ocorrer em cavernas: o tubo A representa a abertura para o meio ambiente exterior e os tubos B e C representam ambientes fechados, onde o ar está aprisionado.
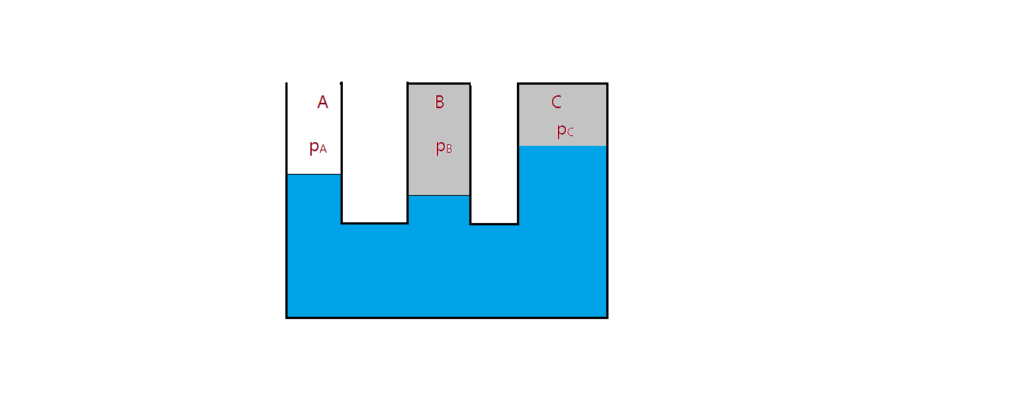
Sendo $p_{A}$ a pressão atmosférica ambiente, $p_{B}$ e $p_{C}$ as pressões do ar confinado nos ambientes B e C, pode-se afirmar que é válida a relação:
( )a) $p_{A}= p_{B} > p_{C}$;
( )b) $p_{A} > p_{V} = p_{C}$;
( )c) $p_{A} > p_{B} > p_{C}$;
( )d) $p_{B} > p_{A} > p_{C}$;
( )e) $p_{B} > p_{C} > p_{A}$.
10. Em um recipiente em formato de U foram colocadas determinadas quantidades de água e óleo. Após haver equilíbrio no sistema, as alturas das colunas de água e óleo a partir de um determinado referencial foram determinadas, sendo $h_{óleo}=100\, mm$ para o óleo e $h_{água}=70\,mm$ para a água. Sabendo que a massa específica da água é $\mu_{H_{2}O}=1000\,kg/m^3$, determine a massa específica do óleo em $kg/m^3$.
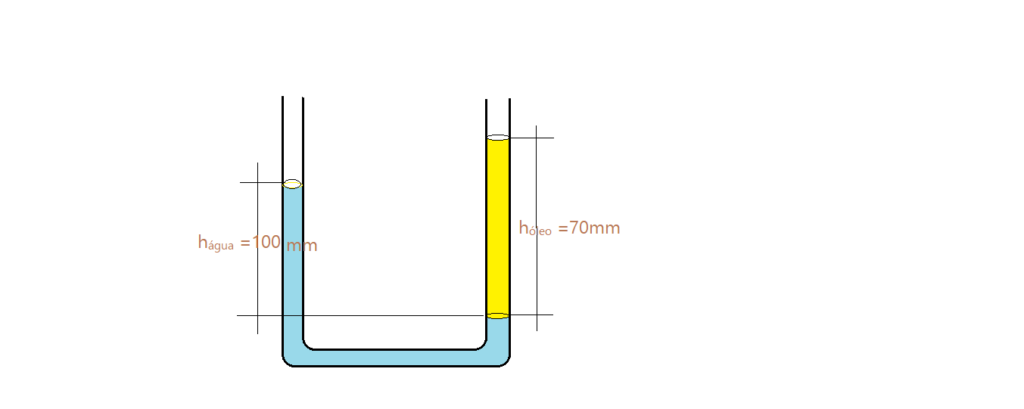
( )a) 500;
( )b) 650;
( )c) 600;
( )d) 700;
( )e) 800;
11. As seguintes afirmações são feitas a respeito de dois líquidos de densidades diferentes colocados juntos em um tubo em formato de U.
I) A determinação da densidade ou altura das colunas de líquido é feita a partir da lei de Stevin;
II) A pressão atmosférica só fará diferença se pelo menos uma das extremidades do recipiente estiver fechada;
III) A menor coluna de líquido sempre será daquele que possui menor densidade;
IV) A pressão para pontos de mesma altura será a mesma.
Marque a alternativa correta.
( )a) As afirmações I, III e IV são verdadeiras;
( )b) As afirmações II e III são falsas;
( )c) Todas as afirmações são verdadeiras;
( )d) Somente I é verdadeira;
( )e) As afirmações I, II e IV são verdadeiras.
Se houver alguma dúvida relativamente aos assuntos abordados, use um dos canais abaixo para fazer contato e solicitar ajuda. Estou à sua disposição.
Curitiba, 31 de julho de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
