Física – Termologia – Dilatometria, Variação da densidade

By decioadams in Dilatometria, Física, Termologia, Termometria 22 de julho de 2020

Vale começar lembrando as formas com que calculamos a densidade. Eu sou um pouco “moda antiga” e me habituei a distinguir “densidade” de “massa específica”, bem como “peso específico”.

Massa específica:

$$\color{Navy}{\mu = \frac{m}{V}}$$

Unidades: $g/cm^3$, $kg/m^3$, $utm/m^3$, $ g/l$.

Obs.: O padrão de comparação das massas específicas é a massa específica da água em seu ponto mais destacado. Na temperatura de $\theta = 3,98^0C$ ela apresenta a massa de $\mu_{o} = 1g/cm^3$. Estudamos isso na dilatação anômala da água. Esse valor é constante, pois é válido somente para estas condições de temperatura e pressão normal.

Densidade: – e a razão entre a massa específica da substância e a massa específica da água na temperatura de $\theta = 3,98^0C$, que geralmente é tomada com arredondamento para $\theta = 4^0C$.

$$\color{Navy}{\delta = \frac{\mu}{\mu_{oH_{2}O}}}$$

Talvez alguém pergunte qual é a unidade e eu respondo que, sendo o quociente entre duas grandezas de mesma natureza, não temos unidade. A densidade é um número puro que indica quantas vezes a unidade de massa padrão é contida por unidade de volume. Em qualquer sistema de unidades, a densidade será a mesma. O fato de o valor da densidade ser igual ao valor da massa específica no sistema de unidades CGS, deve ser visto por uma grande maioria como significando ser densidade e massa específica a mesma coisa.

A partir dessa consideração podemos afirmar que:

$\delta = \frac{\mu}{\mu_{oH_{2}O}}$$\Leftrightarrow$$\color{Maroon}{\mu = \delta\times \mu_{oH_{2}O}}$

Nota de esclarecimento: – Para evitar transtornos, tenha sempre em mente esse detalhe. O termo densidade habitualmente significa “massa específica”, mas na prática esta última tem valores diferentes nos diversos sistemas de unidades.

Basta lembrarmos que:

$1\frac{g}{cm^3} = \frac{10^{-3}}{10^{-6}}\, kg/m^3$$\Leftrightarrow$$\color{Navy}{1\frac{g}{cm^3} = 10^3\,kg/m^3}$

Peso específico: – é a razão entre o peso de um corpo e seu volume.

$$\color{Maroon}{\rho = \frac{P}{V}}$$

Unidades: $dyn/cm^3$, $ N/m^3$, $kgf/m^3$, $gf/cm^3$ e outras semelhantes.

Como o peso é uma grandeza proporcional à aceleração da gravidade, temos por isso:

$$\color{Maroon}{\rho = \mu\times g}$$

Por fim teremos: $$\color{Navy}{\rho = \delta\times\mu_{oH_{2}O}\times g}$$

Até aqui apenas fizemos uma revisão do que foi visto anteriormente sobre o assunto. O objetivo é estabelecer uma relação entre estas grandezas e o fenômeno da dilatação térmica. Sendo tanto a massa específica (densidade) como o peso específico estabelecidos em função do volume, ao desejarmos uma precisão mais acurada, devemos levar em consideração a temperatura, uma vez que dela depende o volume da porção de matéria que estivermos medindo ou avaliando.

Na dilatação levaremos em conta apenas a volumétrica, para a qual temos:

$$\color{Brown}{V = V_{o} + \gamma\times V_{o}\times \Delta\theta}$$

Nas tabelas de coeficientes de dilatação via de regra vem especificada a temperatura na qual os valores fornecidos são válidos. Em pequenos intervalos de temperatura eles habitualmente são considerados constantes. Da mesma forma, os valores das massas específicas ou densidades, também têm seu valor médio fixado para temperaturas próximas da temperatura ambiente em geral. Não havendo necessidade de alta precisão, podemos nos satisfazer com estes valores, já que os desvios serão mínimos de modo geral.

Sendo $$\color{Brown}{\mu_{o} = \frac{m}{V_{o}}}$$

Para uma temperatura mais elevada ou baixa teremos:

$\mu_{f} = \frac{m}{V_{o} + V_{o}\times\gamma\times\Delta\theta}$$\Leftrightarrow$$\color{Navy}{\mu_{f} = \frac{m}{V_{o}\times{(1 + \gamma\Delta\theta)}}}$

Tomando o valor do volume inicial como igual a uma unidade, ficará:

$$\color{NavyBlue}{\mu_{f}= \frac{m}{1 + \gamma\Delta\Theta}}$$

Tomando o valor de $\mu$ no sistema CGS, poderemos fazer também:

$$\color{Sepia}{\delta_{f} = \frac{m}{1 + \gamma\Delta\theta}}$$

A variação de densidade para mais ou para menos, obtemos estabelecendo a diferença entre o valor final e o inicial da mesma.

$$\color{Brown}{\Delta\delta = \delta_{f} – \delta_{o}}$$

Tabela de coeficientes de dilatação volumétrica de algumas substâncias.

Substância	$\gamma=^0C^{-1} = K^{-1}$
Alumínio(Al)	$(66 a 72)\cdot {10}^{-6}$
Latão(CuZn)	$60\cdot {10}^{-6}$
Cobre(Cu)	$51\cdot {10}^{-6}$
Invar(FeNi)	$2,7\cdot {10}^{-6}$
Quartzo(fundido)	$1,2\cdot {10}^{-6}$
Aço	$36\cdot {10}^{-6}$
Álcool etílico	$750\cdot {10}^{-6}$
Dissulfeto de carbono	$1150\cdot {10}^{-6}$
Glicerina	$490\cdot {10}^{-6}$
Mercúrio(Hg)	$180\cdot {10}^{-6}$
Água(H_{2}O)	$1300\cdot {10}^{-6}$
Benzeno	$1060\cdot {10}^{-6}$
Álcool metílico	$1120\cdot {10}^{-6}$
Acetona	$1490\cdot {10}^{-6}$
Petróleo	$1000\cdot {10}^{-6}$
Ouro(Au)	$45\cdot {10}^{-6}$
Vidro comum	$(24 a 27)\cdot {10}^{-6}$
Vidro pyrex	$9,6\cdot {10}^{-6}$
Ferro(Fe)	$36\cdot {10}^{-6}$
Tungstênio	$12,9\cdot {10}^{-6}$
Prata(Ar)	$56,4 a 60)\cdot {10}^{-6}$
Platina	$27\cdot {10}^{-6}$
Zinco(Zn)	$26\cdot {10}^{-6}$
Chumbo(Pb)	$81\cdot {10}^{-6}$

Tabela de coeficientes de dilatação volumétrica de algumas substâncias.

Tabela de densidades de algumas substâncias líquidas.

Substância	Temperatura $^0C $(1)	Densidade em relação água a $ 4^0C$
Ácido acético	25	1,052
Acetona	25	0,787
Acetileno	– 121^0F	0,620
Acetileno	70^0F	0,380
Ácido adípico		0,720
Etanol	25	0,787
Metanol	25	0,797
Propanol	25	0,802
Amônia^(3)	25	0,826
Anilina	25	1,022
Benzeno	25	0,876
Benzil	25	1,084
Bromo	25	3,120
Butano	25	0,601
Ácido caproico	25	0,924
Ácido carbólico	25	0,959
Dissulfeto de carbono	25	1,265
Tetracloreto de carbono	25	1,589
Careno	25	0,860
Óleo de Castor	25	0,959
Cloro	25	1,560
Clorofórmio	25	1,469
Ácido cítrico	25	1,665
Óleo de coco	15	0,927
Óleo de algodão	15	0,929
Cresol	25	1,027
Creosoto	15	1,070
Petróleo(Califórnia)	60^0F	0,918
Petróleo(México)	60^0F	0,976
Petróleo(Texas)	60^0F	0,876
Cumeno(isopropilbenzeno)	25	0,862
Decano	25	0,728
Dodecano	25	0,757
Etano	– 89	0,572
Eter	25	0,716
Etil amina	16	0,683
Etileno-glicol	25	1,100
Flúor(freon) refrig. R-11	25	1,480
Flúor refrigerante R-12	25	1,315
Flúor refrigerante R-22	25	1,197
Formaldeído	45	0,815
Óleo combustível	60^0F	0,893
Furano	25	1,421
Furfural	25	1,159
Gasolina natural	60^0F	0,713
Gasolina de automóvel	60^0F	0,739
Glicerina	25	1,263
Glicerol	25	1,129
Heptano	25	0,681
Hexano	25	0,657
Hexanol	25	0,813
Hexeno	25	0,673
Hidrazina	25	0,797
Querosene	60^0F	0,820
Ácido linolênico	25	0,902
Óleo de linhaça	25	0,932
Mercúrio	25	13,633
Metano	-164	0,466
Leite		1,035
Nafta	15	0,667
Madeira	25	0,701
Naftaleno	25	0,963
Nonanol	25	0,823
Octano	25	0,701
Óleo de oliva	25	0,703
Oxigênio	-183	1,140
Ácido palmítico	25	0,853
Pentano	25	0,755
Fenol	25	1,075
Fosgênio	25	1,381
Fitadieno	25	0,826
Pineno	25	0,858
Propano	-40	0,585
Propano	25	0,495
Propileno	25	0,516
Propilenoglicol	25	1,036
Piridina	25	0,968
Resorcinol	25	1,272
Água do Mar	25	1,028
Água do Mar	77^0F	1,025
Silano	25	0,719
Sorb aldeído	25	0,898
Ácido esteárico	25	0,941
Estireno	25	0,906
Terpeno	25	0,850
Tolueno	25	0,865
Terebentina	25	0,871
Água do Mar Morto	25	1,120
Água pura	$3,98\simeq 4$	1,000

Tabela de densidades de substâncias líquidas.

Exceto onde explicitamente indicada medida em ^0F

Tabela de densidades de alguns materiais sólidos

Substância	$^0C$	Densidade em relação à água a $4^0C$
Alumínio(Al)	25	2,702
Zinco(Zn)	25	7,100
Prata(Ar)	25	10,500
Chumbo(Pb)	25	11,400
Ouro(Au)	25	19,400
Cobre(Cu)	25	8,900
Ferro(Fe)	25	7,860
Madeira	25	0,570 (média)
Concreto	25	2,400
Concreto armado	25	2,500
Argamassa gesso	25	1,400
Arg. cal,areia e cim.	25	1,900
Arg. cimento e areia	25	2,100

Tabela de densidades de alguns materiais.

Exercícios resolvidos

01. Um bloco de alumínio tem $m=54,0\,g$ , na temperatura de $\theta = 75^{0}$. Sabendo que a densidade do metal, a $\theta_{o}= 25^{0}C$ é de $\delta =2,702$ e o coeficiente de dilatação volumétrica é $\gamma = 72\times {{10}^{-6}}^0C^{-1}$, pede-se: a) qual é a densidade na temperatura fornecida? b) qual é o volume ocupado pelo bloco? c) qual foi a variação da densidade?

Dados: $m=54,04\,g$, $\theta_{f}=75^{0}C$, $\delta=2,702$ e $\gamma = 72\times{{10}^{-6}}^0C^{-1}$

a)$$\delta_{f} = \frac{\delta}{1 + \gamma(\theta – \theta_{o})}$$

$\delta_{f} = \frac{2,702}{1 + 72\gamma\times{10}^{-6}}$

$$\delta_{f} = \frac{2,702}{1,000072} =\color{Navy}{ 2,701805}$$

b) $V = \frac{m}{\delta_{f}}$$\Leftrightarrow$$V_{f}=\frac{54,04}{2,701805}$

$$\color{Navy}{V_{f}= 20,0014\,cm^{3}}$$

c)$\Delta\delta = \delta_{f} – \delta_{o}$$\Leftrightarrow$$\Delta\delta=2,701805 – 2,702$

$$\color{Navy}{\Delta\delta = – 1,95\times {10}^{-4}\,g/cm^{3}}$$

02. Uma proveta contém $V_{o} = 50\,ml$ de acetona a $\theta_{o}= 25^0C$. Leva-se o líquido a um freezer, onde atinge a temperatura de $-10^0C$. Se a massa específica do líquido é $\mu_{o} = 0,787 g/cm^{3}$ e o coeficiente de dilatação volumétrica é $\gamma_{Ac}=1490\cdot {{10}^{-6}}^0C^{-1}$. Determine: a) o volume indicado na proveta ao atingir a temperatura final; b) a densidade final do líquido; c)a variação da densidade ocorrida.

Dados:$V_{o}=50\,ml$, $\theta_{o}=25^0C$, $\theta_{f}=-10^0C$, $\mu_{o}= 0,787\,g/cm^{3}$ e $\gamma_{Ac} =1490\times {{10}^{-6}}^0C^{-1}$

a) $$\color{Maroon}{V = V_{o}{(1 + \gamma\cdot \Delta\theta}}$$

$V= 50{(1 + 1490\cdot {10}^{-6}\times (-35)}$$\Leftrightarrow$$V = 50 – 2,06075$

$$\color{Navy}{47,93925 ml}$$

b)$$\color{Sepia}{\delta_{f} = \frac{\delta_{o}}{1 + \gamma\cdot \Delta\theta}}$$

$\delta_{f} = \frac{0,787}{1 + 1490\times {10}^{-6}\times {-35}}$

$\delta_{f} = \frac{0,787}{0,948}$$\Leftrightarrow$$\delta_{f}=0,83\,g/ml$

$$\color{Navy}{\delta_{f}= 0,83\, g/ml}$$

c)$$\color{Maroon}{\Delta\delta = \delta_{f} – \delta_{o}}$$

$\color{Navy}{\Delta\delta = 0,830 – 0,787 = 0,43\, g/ml}$$

Exercícios de vestibular

01. (UFU) Em condições ambientes, a densidade do mercúrio é de aproximadamente $13 g/cm^3$. A massa desse metal, da qual um garimpeiro de Poconé (MT) necessita para encher completamente um frasco de meio litro de capacidade, é de:

a) 2.600 g;
b) 3.200 g;
c) 4.800 g;
d) 6.500 g;
e) 7.400 g.

02. (Unifor) Um corpo sólido, de massa $90\,g$ e volume $100 cm^{3}$, encontra-se no fundo de um recipiente contendo um líquido de massa específica$\mu_{1} = 0,60\,g/cm^{3}$. Misturando-se um outro líquido de massa especifica $\mu_{2}=1,5\,g/cm^{3}$, o corpo começa a flutuar quando a massa específica da mistura, em $g/cm^{3}$, for superior a:

a) 0,90;
b) 1,0;
c) 1,1;
d) 1,2;
e) 1,3.

03. (Mackenzie) No preparo de uma limonada em duas etapas, foram feitas as seguintes observações:

1^a etapa → mistura I	1^a observação
Ao se espremer o limão sobre a água, uma semente escapou e caiu no copo.	A semente imediatamente afundou na mistura.
2^a etapa → mistura II	2^a observação
Na mistura obtida, dissolveram-se três colheres de açúcar.	A semente subiu para a superfície do líquido.

Passos da preparação da limonada.

Das observações 1 e 2, pode-se concluir que a densidade da semente é:

a) menor que a densidade do suco de limão mais água;
b) menor que a densidade do suco de limão mais água e açúcar;
c) igual à densidade do suco de limão;
d) maior que a densidade do suco de limão mais água e açúcar;
e) igual à densidade da água mais açúcar.

04. (UFPE) Para identificar três líquidos — de densidades 0,8; 1,0 e 1,2 — o analista dispõe de uma pequena bola de densidade = 1,0. Conforme a posição das bolas apresentadas no desenho abaixo, podemos afirmar que:

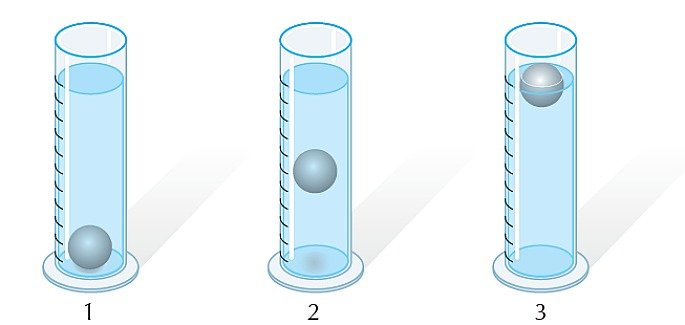
a) os líquidos contidos nas provetas 1, 2 e 3 apresentam densidades 0,8, 1,0 e 1,2;
b) os líquidos contidos nas provetas 1, 2 e 3 apresentam densidades 1,2, 0,8 e 1,0;
c) os líquidos contidos nas provetas 1, 2 e 3 apresentam densidades 1,0, 0,8 e 1,2;
d) os líquidos contidos nas provetas 1, 2 e 3 apresentam densidades 1,2, 1,0 e 0,8;
e) os líquidos contidos nas provetas 1, 2 e 3 apresentam densidades 1,0, 1,2 e 0,8.

05. (UFPI) Em uma cena de um filme, um indivíduo corre carregando uma maleta tipo 007 ($V= 20\,dm^{3}$, cheia de barras de um certo metal. Considerando que um adulto de massa média ($m=70\,kg$) pode deslocar, com uma certa velocidade, no máximo o equivalente à sua própria massa, indique qual o metal contido na maleta, observando os dados da tabela. (Dado: $1\,dm^{3} = 1\,L = 1.000\,cm^{3}$)

Massa específica em $g/cm^{3}$
Alumínio	2,7
Zinco	7,1
Prata	10,5
Chumbo	11,4
Ouro	19,3

a) Alumínio;
b) Zinco;
c) Prata;
d) Chumbo;
e) Ouro.

06. (Enem/2012) Um consumidor desconfia que a balança do supermercado não está aferindo corretamente a massa dos produtos. Ao chegar a casa resolve conferir se a balança estava descalibrada. Para isso, utiliza um recipiente provido de escala volumétrica contendo 1,0 litro d’água. Ele coloca uma porção dos legumes que comprou dentro do recipiente e observa que a água atinge a marca de 1,5 litro e também que a porção não ficara totalmente submersa, 1/3 de seu volume fora d’água. Para concluir o teste, o consumidor, com ajuda da internet, verifica que a densidade dos legumes, em questão, é a metade da densidade da água, onde, $\mu_{água} = 1\,g/cm^{3}$. No supermercado a balança registrou a massa da porção de legumes igual a $m =0,500\,kg$ (meio quilograma). Considerando que o método adotado tenha boa precisão, o consumidor concluiu que a balança estava descalibrada e deveria ter registrado a massa da porção de legumes igual a:

a) 0,073 kg;
b) 0,167 kg;
c) 0,250 kg;
d) 0,375 kg;
e) 0,750 kg.

07. (Enem/2016) Densidade absoluta (d) é a razão entre a massa de um corpo e o volume por ele ocupado. Um professor propôs à sua turma que os alunos analisassem a densidade de três corpos: dA, dB, dC. Os alunos verificavam que o corpo A possuía 1,5 vez a massa do corpo B e esse, por sua vez, tinha 3/4 da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.

Após a análise, os alunos ordenaram corretamente as densidades desses corpos da seguinte maneira.

a) dB < dA < dC;
b) dB = dA < dC;
c) dC < dB = dA;
d) dB < dC < dA;
e) dC < dB < dA.

08. (Enem/2001) Pelas normas vigentes, o litro do álcool hidratado que abastece os veículos deve ser constituído de 96% de álcool puro e 4% de água (em volume). As densidades desses componentes são dadas na tabela.

Substância	Massas específicas (g/L)
Água	1000
Álcool	800

Dados do exercício.

Um técnico de um órgão de defesa do consumidor inspecionou cinco postos suspeitos de venderem álcool hidratado fora das normas. Colheu uma amostra do produto em cada posto, mediu a densidade de cada uma, obtendo:

Posto	Massa específica do combustível (g/L)
I	822
II	820
III	815
IV	808
V	805

Massas específicas de líquidos combustíveis.

A partir desses dados, o técnico pôde concluir que estavam com o combustível adequado somente os postos

a) I e II;
b) I e III;
c) II e IV;
d) III e V;
e) IV e V.

09. (Enem/2009) O controle de qualidade é uma exigência da sociedade moderna na qual os bens de consumo são produzidos em escala industrial. Nesse controle de qualidade são determinados parâmetros que permitem checar a qualidade de cada produto. O álcool combustível é um produto de amplo consumo muito adulterado, pois recebe adição de outros materiais para aumentar a margem de lucro de quem o comercializa. De acordo com a Agência Nacional de Petróleo (ANP), o álcool combustível deve ter densidade entre $0,805\,g/cm^{3}$ e $0,811\,g/cm^{3}$. Em algumas bombas de combustível a densidade do álcool pode ser verificada por meio de um densímetro similar ao desenhado abaixo, que consiste em duas bolas com valores de densidade diferentes e verifica quando o álcool está fora da faixa permitida. Na imagem, são apresentadas situações distintas para três amostras de álcool combustível.

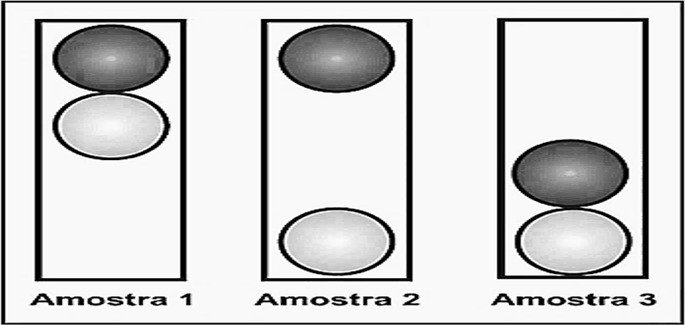
A respeito das amostras ou do densímetro, pode-se afirmar que

a) a densidade da bola escura deve ser igual a $0,811\,g/cm^{3}$;
b) a amostra 1 possui densidade menor do que a permitida.
c) a bola clara tem densidade igual à densidade da bola escura.
d) a amostra que está dentro do padrão estabelecido é a de número 2.
e) o sistema poderia ser feito com uma única bola de densidade entre $0,805\,g/cm^{3} e $0,811\,g/cm^{3}.

10. (Enem/2010) Com a frequente adulteração de combustíveis, além de fiscalização, há necessidade de prover meios para que o consumidor verifique a qualidade do combustível. Para isso, nas bombas de combustíveis existe um densímetro, semelhante ao ilustrado na figura. Um tubo de vidro fechado fica imerso no combustível, devido ao peso das bolinhas de chumbo colocadas no seu interior. Uma coluna vertical central marca a altura de referência, que deve ficar abaixo ou no nível do combustível para indicar que sua densidade está adequada. Como o volume do líquido varia com a temperatura mais que o do vidro, a coluna vertical é preenchida com mercúrio para compensar variações de temperatura.

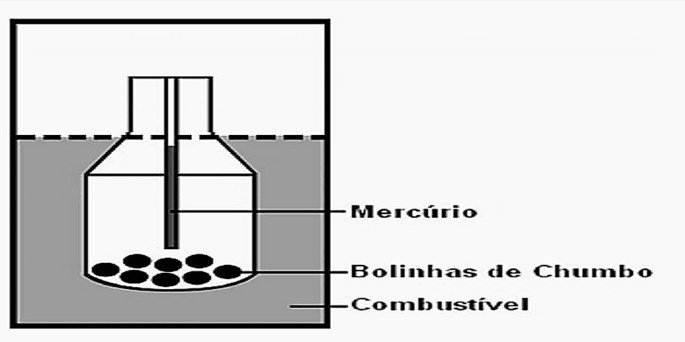
De acordo com o texto, a coluna vertical de mercúrio, quando aquecida,

a) indica a variação da densidade do combustível com a temperatura;
b) mostra a diferença de altura da coluna a ser corrigida;
c) mede a temperatura ambiente no momento do abastecimento;
d) regula a temperatura do densímetro de acordo com a do ambiente;
e) corrige a altura de referência de acordo com a densidade do líquido.

11. Uma solução foi preparada misturando-se $m_{sal}=30\,g}$ de um sal em $m = 300\,g$ de água. Considerando-se que o volume da solução é igual a $V=300\,mL$, a densidade dessa solução em $g/mL$ será de:

a) 10,0;

b) 1,0;

c) 0,9;

d) 1,1;

e) 0,1.

12. Três líquidos (água, benzeno e clorofórmio) foram colocados numa proveta, originando o seguinte aspecto:

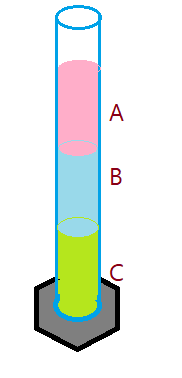
A seguir temos uma tabela com as densidades de cada líquido. Baseando-se nessas informações e em seus conhecimentos sobre densidade, relacione as substâncias A, B e C com as mencionadas na tabela. Justifique sua resposta. Consulte a tabela de densidades fornecida antes.

13. Na tabela abaixo temos as densidades de alguns materiais sólidos. Se eles forem adicionados à água líquida e pura, à temperatura ambiente, qual deles flutuará?

Pau-brasil ………………………… 0,4 g/cm^{3};
Alumínio ………………………….. 2,70 g/cm^{3};
Diamante ……………………………3,5 g/cm^{3};
Chumbo……………………………..11,3 g/cm^{3};
Carvão ………………………………. 0,5 g/cm^{3};
Mercúrio ……………………………13,6 g/cm^{3};
Água ………………………………….. 1,0 g/cm^{3}

14. Uma solução aquosa foi preparada dissolvendo-se certa massa de hidróxido de sódio (NaOH) em 600\,mL de água, originando um volume de 620\,mL. Qual será a massa do soluto presente nessa solução? (Dados: densidade da solução = 1,19\,g/mL; densidade da água = 1,0\,g/mL)

a) 222,4 g;

b) 137,8 g;

c) 184,5 g;

d) 172,9 g;

e) 143,1 g.

15. (Fuvest-SP) – Em uma indústria, um operário misturou, inadvertidamente, polietileno (PE), policloreto de vinila (PVC) e poliestireno (PS), limpos e moídos. Para recuperar cada um destes polímeros, utilizou o seguinte método de separação: jogou a mistura em um tanque contendo água $\mu = 1,00\,g/cm^{3}$, separando, então, a fração que flutuou (fração A) daquela que foi ao fundo (fração B). Depois, recolheu a fração B, secou-a e jogou-a em outro tanque contendo solução salina $\mu_{2} = 1,10\,g/cm^{3}$, separando o material que flutuou (fração C) daquele que afundou (fração D).

(Dados: densidade na temperatura de trabalho em $g/cm^{3}$, polietileno = 0,91 a 0,98; poliestireno = 1,04 a 1,06; policloreto de vinila = 1,5 a 1,42)

As frações A, C e D eram, respectivamente:

a) PE, PS e PVC;

b) PS, PE e PVC;

c) PVC, PS e PE;

d) PS, PVC e PE;

e) PE, PVC e PS.

16. (Unicamp-SP) Três frascos de vidro transparentes, fechados, de formas e dimensões iguais, contêm cada um a mesma massa de líquidos diferentes. Um contém água, o outro, clorofórmio e o terceiro, etanol. Os três líquidos são incolores e não preenchem totalmente os frascos, os quais não têm nenhuma identificação. Sem abrir os frascos, como você faria para identificar as substâncias?

A densidade (d) de cada um dos líquidos, à temperatura ambiente, é:

$\mu_{H_{2}O} = 1,0\,g/cm^{3}$

$\mu_{clor} = 1,4\,g/cm^{3}$

$\mu_{etan} = 0,8\,g/cm^{3}$

17. (FMU-SP) Um vidro contém $V = 200\,cm^{3}$ de mercúrio de massa específica é $\mu_{Hg} = 13,6\,g/cm^{3}$. A massa de mercúrio contido no vidro é:

a) 0,8 kg;

b) 0,68 kg;

c) 2,72 kg;

d) 27,2 kg;

e) 6,8 kg.

Havendo dúvidas, faça contato por um dos canais abaixo listados e sanaremos suas dificuldades.

Curitiba, 22 de julho de 2020.