Física – Mecânica, Movimentos Compostos.
Um corpo pode estar animado de diferentes velocidades em diferentes direções. Isso determina diferentes formas de trajetórias, resultantes dos deslocamentos ocorridos em cada direção. O primeiro caso é o denominado lançamento horizontal.
Lançamento horizontal
O lançamento horizontal inicia-se com uma velocidade horizontal que algum dispositivo imprime ao móvel, além de ficar sob a ação da aceleração da gravidade. Dentro dos limites aceitáveis, a componente horizontal da velocidade é constante, enquanto a vertical é crescente, até o instante de atingir o solo. Isso resulta num movimento em forma de parábola, pois os deslocamentos horizontais são iguais e os verticais são crescentes com o tempo. Vejamos a figura que ilustra a situação.
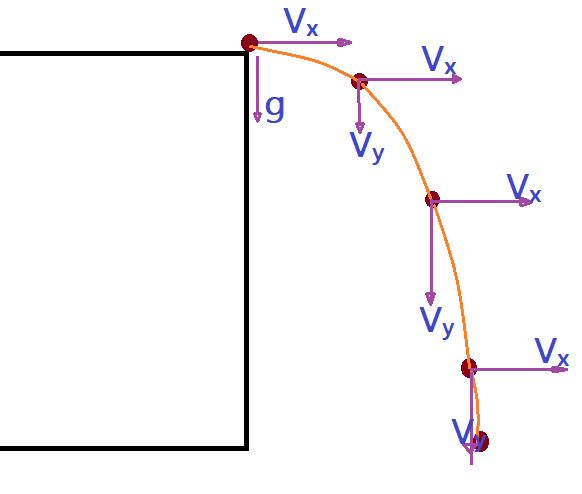
Neste caso os cálculos podem ser resolvidos com as equações do MRU e MRUV, conforme o eixo que estejamos visando. As posições são caracterizadas por um par ordenado ${(x, y)}$, sendo $x$ a abcissa horizontal e $y$, a ordenada vertical.
A velocidade horizontal é constante: $\color{Blue}{V_{X}}$$\rightarrow$ é constante.
A velocidade vertical cresce com o tempo de acordo com a equação da velocidade do MRUV (queda livre).
$\color{Blue}{V_{Y} =- g\cdot t}$
As posições do móvel são determinadas pelas coordenadas $(X, Y)$.
$\color{Blue}{X = V_{X}\cdot t}$$\rightarrow$ MRU.
$\color{Blue}{Y = Y_{0} – \frac{1}{2}\cdot g\cdot t^{2} }$
Aplicação.
01. Tomemos o caso de uma esfera que é lançada de um ponto situado a $Y_{0} = 20,0\,m$, com a velocidade $V_{X}= 15,0\, m\cdot{s^{-1}}$. Sendo a aceleração da gravidade local $g = 10,0\, m\cdot{s^{-2}}$, determine o tempo que o corpo demora no ar, o alcance horizontal e a velocidade com que ela atinge o solo.
O tempo gasto no movimento equivale ao movimento de queda livre de um corpo abandonado na mesma altura. Temos a posição inicial $Y_{0} =20,0\, m$ e no instante que toca o chão, a altura é $Y = 0$.
$Y = Y_{0} – \frac{1}{2}\cdot g\cdot t^{2}$
$0 = 20,0 – \frac{1}{2}\cdot{10,0}\cdot t^{2}$$\Leftrightarrow$$ -20,0 = -5\cdot t^{2}$
$t^{2} = \frac{-20,0}{-5,0}$$\Leftrightarrow$$\sqrt{t^{2}} = \sqrt{4}$
$t = \pm {2,0}$
O tempo não admite sinal negativo e por isso o resultado é:
$\color{Brown}{ t = {2,0}\, s}$
O alcance será determinado usando a equação horária do MRU, para o instante determinado acima.
$X = V_{X}\cdot t$
$X = {15,0}\cdot {2,0}$$\Leftrightarrow$$X = {30,0}\, m$
$\color{Brown}{X = {30,0}\, m}$
A velocidade é composta de duas componentes. A horizontal $V_{X}$ e a vertical $V_{Y}$
$V_{Y}= – g\cdot t$
$V_{Y}= – {10,0}\cdot {2,0}$$\Leftrightarrow$$V_{Y}= {-20,0}\, m\cdot{s^{-1}}$
As duas componentes formam um ângulo reto e usaremos o Teorema de Pitágoras para chegar ao final.
$V^{2} = {V_{x}}^{2} + {V_{Y}}^{2}$$\Leftrightarrow$$V^{2}={15,0}^{2} + {- 20,0}^{2}$
$V^{2} = {225,0} + {400,0}$$\Leftrightarrow$$\sqrt{V^{2}}=\sqrt{625,0}$
$\color{Brown}{V = {25,0}\, m\cdot{s^{-1}}}$
A direção da velocidade pode ser determinada pelo valor da tangente do ângulo formado abaixo da horizontal.
$tg\alpha = \frac{V_{Y}}{V_{X}}$
$tg\alpha = \frac{-20,0}{15,0}$$\Leftrightarrow$$tg\alpha = -\frac{4}{3}$
$tg\alpha = – 1,333$
$\color{Brown}{\alpha = arctg (-1,333)}$
O sinal negativo significa que o ângulo fica abaixo da horizontal. A medida do ângulo é de
$\color{Blue}{\alpha \simeq – 53^{0}}$
02. Uma bola de sinuca rola sobre uma plataforma horizontal, de altura igual a $1,2\, m$ e se precipita para o chão. Se ela atinge o solo a uma distância $X = 0,98\, m$, considerando a aceleração da gravidade $g=10,0 m\cdot{s^{-2}}$, qual era a velocidade da bola ao deixar a borda da plataforma? Qual é a velocidade no momento do impacto com o chão?
Precisamos determinar o tempo gasto na queda.
$Y = Y_{0} – \frac{1}{2}\cdot g\cdot t^{2}$
$0 = 1,2 – \frac{1}{2}\cdot{10,0}{t^{2}}$$\Leftrightarrow$$ -1,2 = -5\cdot t^{2}$
$t^{2} = \frac{-1,2}{-5,0}$$\Leftrightarrow$$\sqrt{t^{2}}= \sqrt{0,24}$
$\color{Green}{t \simeq 0,49\, s}$
$X = V_{X}\cdot t$$\Leftrightarrow$$0,98 = V_{X}\cdot{0,49}$
$V_{X} = \frac{0,98}{0,49}$$\Leftrightarrow$$\color{Brown}{ V_{X} = 2,0\, m\cdot{s^{-1}}}$
A velocidade será resultante da componente horizontal $V_{X}$ e $V_{Y}$.
$V_{Y} = – g\cdot t$$\Leftrightarrow$$ V_{Y}= -10,0\cdot{0,49}= -4,9 m\cdot{s^{-1}}$
$V^{2} = {V_{X}}^{2} + {V_{Y}}^{2}$$\Leftrightarrow$$V^{2}={2,0}^{2} + {-4,9}^{2}$
$V^{2} = 4,0 + 24,01 = 28,01$$\Leftrightarrow$$\sqrt{V^{2}}= \sqrt{28,01}$
$\color{Brown}{V = 5,29\, m\cdot{s^{-1}}}$
Direção da velocidade.
$tg\alpha = \frac{-4,9}{2,0}$$\Leftrightarrow$$tg\alpha = -2,45$
$\color{Blue}{\alpha = arctg{- 2,45}}$
$\color{Brown}{\alpha \simeq {-68^{0}}}$
Exercite a vontade
01. Um dispositivo lançador é disposto horizontalmente e imprime velocidade $V_{X}=50,0\, m\cdot{s^{-1}}$ e está colocado a uma altura $Y_{0}= {40,0}\,m$. Ele lança um projétil nessa posição. Pergunta-se: a) quanto tempo esse projétil fica no ar? b) qual é a componente vertical da velocidade no instante em que o projétil toca o solo? c) qual é o alcance ($X$) do projétil? d) determine a velocidade resultante ao tocar o solo. Considere a gravidade com valor $g={10,0}\, m\cdot{s{-2}}$
02. Um projétil é disparado por um fuzil com velocidade horizontal $V_{X}={800,0}\, m\cdot{s^{-1}}$. O disparo é realizado a uma altura de $y_{0}= 1,8\, m$. Considerando a aceleração da gravidade $g = 9,8\, m\cdot{s^{-2}}$, pergunta-se: a) quanto tempo dura o movimento do projétil? b) qual é a velocidade vertical no momento do impacto com o solo? c) qual é o alcance do projétil? d) qual é a velocidade resultante ao final do movimento.
03. (CEFET) – Uma bola de pingue-pongue rola sobre uma mesa com velocidade constante de $v_{X}=2m\cdot {s^{-1}}$. Após sair da mesa, cai, atingindo o chão a uma distância de $X = 0,80\, m$ dos pés da mesa. Adote $g= 10 m\cdot {s^{-2}}$, despreze a resistência do ar e determine:
a) a altura da mesa.
b) o tempo gasto para atingir o solo.
04. (Unic-MT) – Considere uma pedra sendo lançada horizontalmente do alto de um edifício de $Y_{0}={125,0}\, m$ de altura, em um local onde o módulo da aceleração da gravidade é igual a $g=10,0\, m\cdot{s^{-2}}$ e tendo um alcance horizontal igual a $x=10,0\, m$. Nessas condições, conclui-se que a velocidade com que a pedra foi lançada, em m/s, tem que valor?
05. Um avião bombardeiro voa a uma altura de $Y_{0}=1500,0\, m$ de altura, com velocidade horizontal de $V_{X}=900,0\, km\cdot{h^{-1}}$. A aceleração da gravidade é de $g = {10,0}\, m\cdot{s^{-2}}$. Em quanto tempo uma bomba solta pelo avião atinja o solo? Qual é a distância horizontal que a bomba irá percorrer até atingir o chão? Supondo a resistência do ar próxima de zero, com que velocidade a bomba chega ao chão?
06. Um dispositivo lançador horizontal é regulado para disparar bolas de sinuca, num ritmo uniforme. A altura do lançamento é $Y_{0}=45,0\, m$ e a velocidade de saída das bolas é $V_{X}= 5,0\, m\cdot{s^{-1}}$. Sendo a aceleração da gravidade $g = 10,0\, m\cdot s^{-1}$, observa-se que quando a primeira bola toca o solo, a quarta inicia seu movimento. Determine os valores dos tempos de movimento de cada bola nesse instante, a velocidade e as coordenadas de posição $(X,Y)$, de modo a determinar a trajetória parabólica das mesmas.
07. (Unic-MT) – Considere uma pedra sendo lançada horizontalmente do alto de um edifício de 125,0 m de altura, em um local onde o módulo da aceleração da gravidade é igual a 10 m/s2 e tendo um alcance horizontal igual a 10,0 m. Nessas condições, conclui-se que a velocidade com que a pedra foi lançada, em m/s, é igual a:
( )a) 2;
( )b) 3;
( )c) 4;
( )d) 5;
( )e) 6.
08. Uma esfera de $m = 0,5\,kg$ rola sem atrito sobre a superfície de uma mesa plana a uma velocidade de $v_{x}=2,0\,m/s$. Sabendo que a altura dessa mesa é de $y_{o}=0,8\,m$, determine o alcance da bola. (Dado: $g = 10,0\,m/s^{2}$).
( )a) 0,8 m;
( )b) 2,4 m;
( )c) 1,6 m;
( )d) 0,4 m;
( )e) 1,2 m.
09. Considere as afirmativas seguintes acerca do movimento de lançamento horizontal, para isso desconsidere a ação da força de resistência do ar.
I – O tempo de queda de objetos lançados horizontalmente é proporcional à raiz quadrada da altura de queda.
II – O tempo de queda no lançamento horizontal depende da massa do corpo: quanto maior for essa massa, menor será o tempo de queda.
III – O tempo de queda de um corpo que se move em lançamento horizontal depende da velocidade horizontal do corpo.
IV – Na direção vertical, o movimento de um objeto lançado horizontalmente é uniformemente acelerado.
São verdadeiras:
( )a) II e III;
( )b) I e IV;
( )c) II, III e IV;
( )d) somente II;
( )e) II e IV.
10. Uma bala de canhão é disparada horizontalmente, a uma velocidade de $v_{x}=600\,m/s$, à beira de um penhasco de $y_{o}=800\,m$de altura. Desconsidere a resistência do ar e determine o valor aproximado do alcance horizontal dessa bala. (Dado: $g = 10\,m/s^{2}$)
( )a) 3850 m;
( )b) 1525 m;
( )c) 7590 m;
( )d) 6490 m;
( )e) 9550\,m.
11. A respeito do lançamento horizontal que ocorre livre de forças dissipativas, assinale a alternativa correta:
( )a) O alcance do projétil lançado horizontalmente depende da massa do corpo, uma vez que corpos mais massivos atingirão distâncias maiores;
( )b) A energia mecânica do objeto lançado horizontalmente aumenta a cada instante;
( )c) O tempo de queda de um objeto lançado horizontalmente não depende da altura do ponto de lançamento em relação ao chão;
( )d) No lançamento horizontal, o movimento que ocorre na direção vertical é uniformemente retardado;
( )e) Nesse tipo de lançamento, a força peso é sempre perpendicular ao deslocamento horizontal e, por isso, não realiza trabalho nessa direção.
12. (Uncisal-AL) – Num experimento, são utilizadas duas bolas de bilhar idênticas, um lançador de bolas horizontal e um ambiente com ar muito rarefeito, de maneira que os corpos em movimento apresentam resistência do ar desprezível. Por meio de sensores e fotografia estroboscópica, o experimento consiste em acompanhar o tempo de queda das duas bolas e caracterizar o tipo de movimento que elas descrevem durante a queda. As duas são colocadas numa mesma altura inicial (h), ficando a bola (B) sobre uma plataforma. A bola (A) é abandonada no mesmo instante que a bola (B) é lançada horizontalmente com velocidade V.
Assumindo que a aceleração da gravidade é constante, é correto afirmar que:
( )a) a bola (A) tem o tempo de queda menor que o tempo de queda da bola (B);
( )b) a bola (A) tem o tempo de queda maior que o tempo de queda da bola (B);
( )c) os tempos de queda das duas bolas são iguais e a bola (B) descreve um movimento uniforme;
( )d) as duas componentes da velocidade da bola (B) são descritas por um movimento uniforme variado;
( )e) os tempos de queda das duas bolas são iguais e a bola (A) descreve um movimento uniforme variado.
13. (Unic-MT)-Considere uma pedra sendo lançada horizontalmente do alto de um edifício de $y_{o}=125,0\,m$ de altura, em um local onde o módulo da aceleração da gravidade é igual a $g = 10\,0\,m/s^{2}$ e tendo um alcance horizontal igual a $x_{t}=10,0\,m$. Nessas condições, conclui-se que a velocidade com que a pedra foi lançada, em $m/s$ é igual a:
( )a) 2;
( )b) 3;
( )c) 4;
( )d) 5;
( )e) 6.
14. Um objeto foi lançado horizontalmente do alto de um arranha-céu de $y_{o}=320\,m$ de altura, com uma velocidade de $v_{x} = 15,0\,m/s$. Determine o alcance horizontal do objeto.
( )a) 100 m;
( )b) 120 m;
( )c) 150 m;
( )d) 130 m;
( )e) 110 m.
15. Determine o alcance horizontal, em metros, de um objeto que foi lançado horizontalmente de uma certa altura, com velocidade de $v_{x}= 10,0\,m/s$, sabendo que o tempo de queda foi de $t_{q}= 2,5\,s$.
( )a) 15;
( )b) 20;
( )c) 25;
( )d) 28;
( )e) 24.
16. (PUC-RJ) – Um pacote do correio é deixado cair de um avião que voa horizontalmente com velocidade constante. Podemos afirmar que (desprezando a resistência do ar):
( )a) um observador no avião e um observador em repouso no solo veem apenas o movimento vertical do objeto;
( )b) um observador no avião e um observador em repouso no solo veem apenas o movimento horizontal do objeto;
( )c) um observador no solo vê apenas um movimento vertical do objeto, enquanto um observador no avião vê o movimento horizontal e vertical;
( )d) um observador no solo vê apenas um movimento horizontal do objeto, enquanto um observador no avião vê apenas um movimento vertical;
( )e) um observador no solo vê um movimento horizontal e vertical do objeto, enquanto um observador no avião vê apenas um movimento vertical.
17. (FUVEST-SP) – Uma menina, segurando uma bola de tênis, corre com velocidade constante, de módulo igual a $V_{x}=10,8\,km/h$, em trajetória retilínea, numa quadra plana e horizontal.
Num certo instante, a menina, com o braço esticado horizontalmente ao lado do corpo, sem alterar o seu estado de movimento, solta a bola, que leva $t_{q}=0,5\,s$ para atingir o solo.
As distâncias $S_{m}$ e $S_{b}$ percorridas, respectivamente, pela menina e pela bola, na direção horizontal, entre o instante em que a menina soltou a bola ($t_{o} = 0\,s$) e o instante $t_{1} = 0,5\,s$, valem:
( )a)$S_{m} = 1,25\,m$ e $S_{b}= 0\,m$;
( )b)$S_{m} = 1,25\,m$ e $S_{b}= 1,50\,m$; ( )c)$S_{m} = 1,50\,m$ e $S_{b}= 0\,m$;
( )d)$S_{m} = 1,50\,m$ e $S_{b} =1,25\,m$;
( )e)$S_{m} = 1,50\,m$ e $S_{b} = 1,50\,m$.
18. (CEFET-MG) – Três pedras são atiradas horizontalmente, do alto de um edifício, tendo suas trajetórias representadas a seguir.
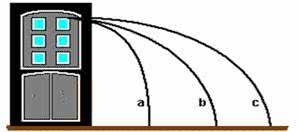
Admitindo-se a resistência do ar desprezível, é correto afirmar que, durante a queda, as pedras possuem:
( )a) acelerações diferentes;
( )b) tempos de queda diferentes;
( )c) componentes horizontais das velocidades constantes;
( )d) componentes verticais das velocidades diferentes, a uma mesma altura;
( )e)N.d.a.
19. (UFSM/2013) – Um trem de passageiros passa em frente a uma estação, com velocidade constante em relação a um referencial fixo no solo. Nesse instante, um passageiro deixa cair sua câmera fotográfica, que segurava próxima a uma janela aberta. Desprezando a resistência do ar, a trajetória da câmera no referencial fixo do trem é _______________, enquanto, no referencial fixo do solo, a trajetória é ___________. O tempo de queda da câmera no primeiro referencial é ___________ tempo de queda no outro referencial.
Assinale a alternativa que completa corretamente as lacunas.
- A – parabólica – retilínea – menor que o
- B – parabólica – parabólica – menor que o
- C – retilínea – retilínea – igual ao
- D – retilínea – parabólica – igual ao
- E – parabólica – retilínea – igual ao
20. (CEFET-CE) – Um aluno do CEFET em uma partida de futebol lança uma bola para cima, numa direção que forma um ângulo de $\gamma = 60^{o}$ com a horizontal. Sabendo que a velocidade na altura máxima é $v_{xm}= 20,0\,m/s$, podemos afirmar que a velocidade de lançamento da bola, em m/s, foi de:,
( )a) 10;
( )b) 17;
( )c) 20;
( )d) 30;
( )e) 40.
21. (CEFET-CE) – Para se posicionar frente ao gol adversário, um jogador efetua deslocamentos rápidos e sucessivos em linha reta, com módulos de 1,8 m e 2,4 m, deixando completamente para trás a defesa oponente. Para que o deslocamento resultante da bola seja de 3,0 m, o ângulo entre estes deslocamentos deve ser de:
( )a) $0^{o}$;
( )b) $30^{o}$;
( )c) $60^{o}$;
( )d) $90^{o}$;
( )e) $120^{o}$.
Se lhe restarem dúvidas, entre em contato comigo para esclarecimentos. Não custa nada, apenas o tempo de ligar ou mandar mensagem.
Curitiba, 24 de abril de 2020.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
