Física – Mecânica, Elasticidade
Vamos dedicar um post ao estudo dos fenômenos de elasticidade. Desde muito cedo na vida, convivemos com materiais elásticos em diferentes formas e aplicações. São fitas de elástico usadas em peças de roupas, câmaras de ar nos pneus dos veículos, no interior das bolas, os balões ou bexigas que enchemos nos aniversários e outras festas. Os meninos do interior se divertem usando os “bodoques”, ou “estilingues”, também chamados de “funda”. São feitos com duas tiras de borracha, uma forquilha e uma peça de couro ou outro material resistente e flexível. Pensa que acabou? Tem muito mais. O fenômeno da elasticidade é algo presente em todos os materiais ou pelo menos na grande maioria. É mais ou menos intenso, dependendo da composição do corpo, das suas dimensões e outras características.
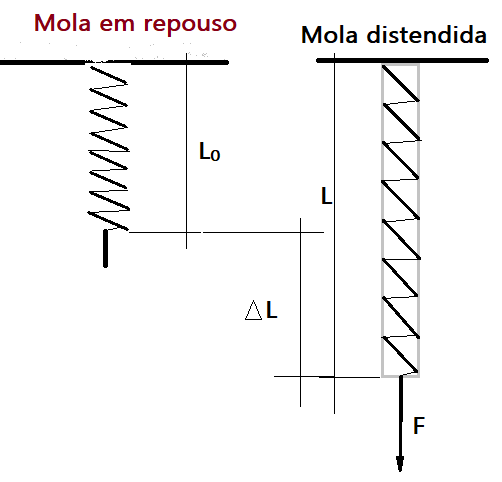
A figura representa esquematicamente uma mola sem aplicação de nenhuma força e ao lado, com uma força produzindo uma deformação.
A experiência demonstra que a deformação $\Delta L$ produzida é proporcional à intensidade da força deformante.
$\color{Blue}{\frac{F}{\Delta L} = k }$
$\color{Green}{F= k {\Delta L} }$
Lei de Hooke
Robert Hooke, cientista experimental inglês, nasceu na ilha de Wihgt em 18/07/1635 e morreu em 03/03/1703. Fez experiências importantes sobre a elasticidade, que resultaram nessa lei. Foi o descobridor da “célula”, usando microscópio para observar um pedaço de cortiça.
“A força elástica é diretamente proporcional à deformação por ela causada”.
A unidade da constante é o quociente da unidade de força pela unidade de comprimento.
a) SI antigo MKS: N/m.
b) MKgfS: kgf/m
c) CGS: dyn/cm.
Vamos aplicar a equação.
01. Determinar a constante elástica de uma mola que, sob a ação de uma força $F = {120,0}N$, se distende de um comprimento inicial $L_{0} = {0,60} m$ para um comprimento final $L = {0,90}m $.
$F = k\cdot {\Delta L}$
$k = \frac{F}{\Delta L}$$\Leftrightarrow$$k = \frac{120,0}{0,90 – 0,60}$
$k = \frac{120,0}{0,30}$$\Leftrightarrow$$ k = 400,0 N/m$
$\color{Brown}{k = 400,0 N/m}$
02. Um estilingue é feito com duas tiras de borracha de $L_{0} = 0,25 m$. Se a constante elástica de cada uma delas é $k = {25,0} kgf/m$, qual é a intensidade da força que atua sobre a pedra usada como projétil, se for distendido até alcançar $L = {0,45}m$.
Sendo duas tiras juntas a constante elástica de uma delas será dobrada.
$k =2\cdot k = {25,0}\cdot 2 = {50,0} kgf/m$
$F = k\cdot {(L – L_{0})}$$\Leftrightarrow$$ F = {50,0}\cdot {(0,45 – 0,25)}$
$F = {50,0}\cdot {0,20} = 10,0 kgf$
$\color{Brown}{F = 10,0 kgf}$
03. Uma mola tem constante elástica $k = 700,0 kgf/m$. Sendo submetida a uma força de tração igual a $F = 280,0 kgf$, qual é a deformação que ela sofre?
$F = k\cdot {\Delta L}$$\Leftrightarrow$$ \Delta L = \frac{F}{k}$
$\Delta L = \frac{280,0}{700,0} = 0,4 m$
$\color{Brown}{\Delta L = 0,4\, m$
Tipos de deformações elásticas
Até aqui usamos apenas um tipo de deformação dos corpos. Mas há outros.
Tração – é o tipo que usamos até aqui. Uma força aplicada em uma extremidade produz um alongamento do corpo.
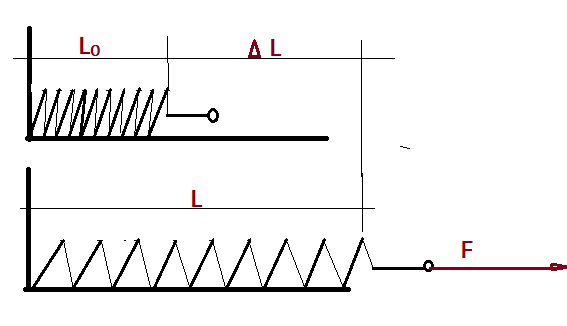
Compressão – a compressão ocorre quando uma força é aplicada sobre um ponto ou extremidade do corpo, causando um encurtamento ou redução da medida.
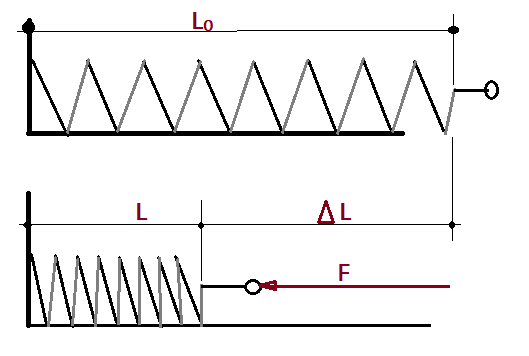
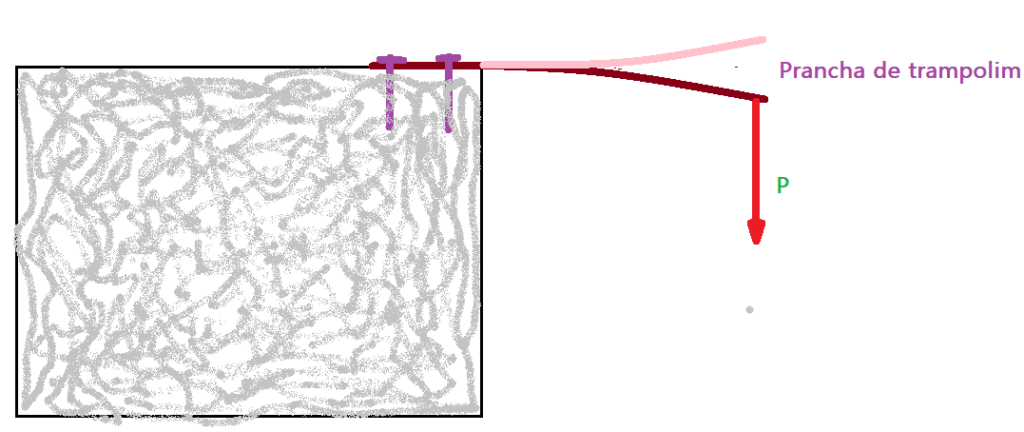
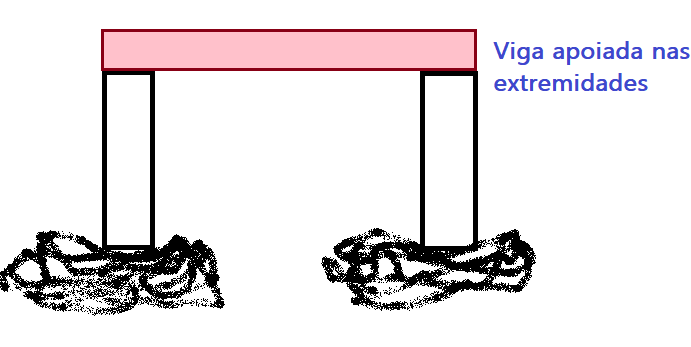
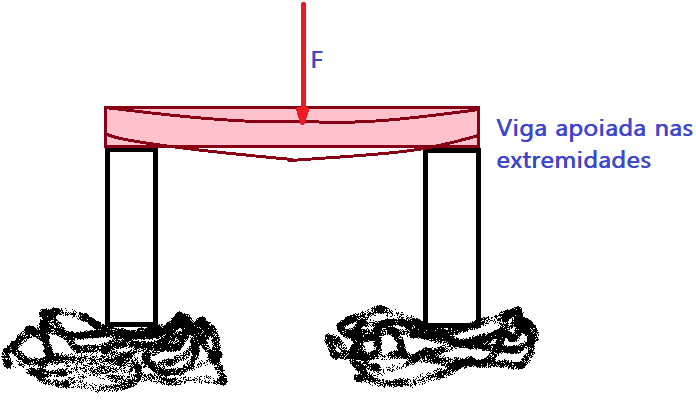
Flexão – ocorre a deformação por flexão quando uma força é aplicada sobre uma extremidade livre ou sobre um ponto sem apoio (vão livre) de uma barra ou lâmina. O corpo se curva durante a ação da força e depois volta ao normal. Nota-se um maior ou menor número de vibrações, conforme a elasticidade e as dimensões do corpo vibrante, quando se trata de flexão semelhante a uma lâmina, com a força aplicada na extremidade.
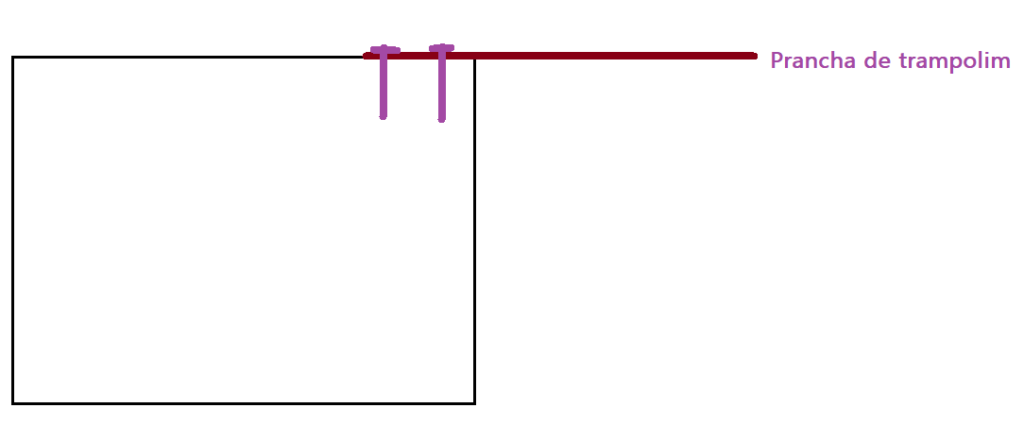
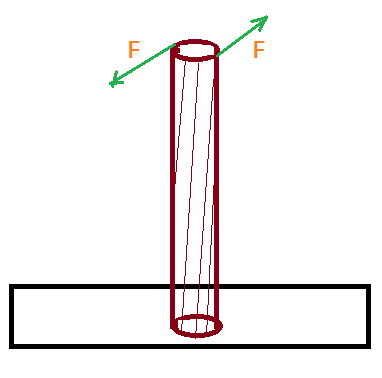
Torção – uma haste ou barra fixada em uma de suas extremidades, sob a ação de um sistema binário, sofre uma torção. Esse tipo de deformação elástica tem muitas aplicações práticas na indústria especialmente. Para citar um exemplo, podemos observar o sistema de suspensão de um carro como o exemplo do famoso “fusca”.
Limite de elasticidade
Não há necessidade de grande poder de observação para perceber que a Lei de Hooke tem validade dentro de um limite. Além desse limite a proporcionalidade entre a força e a deformação deixa de existir.
“O limite de elasticidade é a tensão deformante que o corpo suporta, sem que a deformação se torne permanente”.
Podemos analisar graficamente, representando num plano cartesiano $F=f{\Delta L}$.
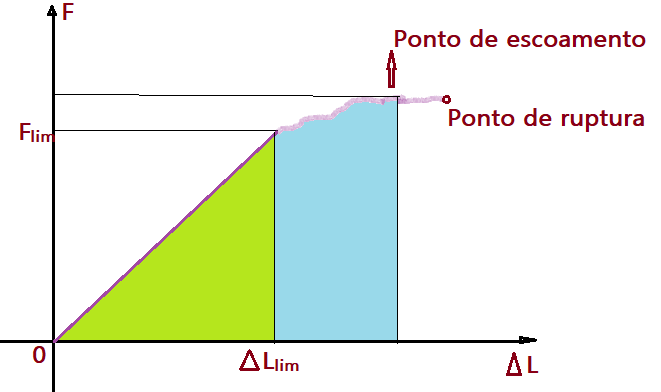
No trecho em que o gráfico é uma reta a força deformante e a deformação são diretamente proporcionais. Para forças além desse ponto, o gráfico perde a linearidade e temos a fase das deformações permanentes. Em certo ponto começa a ocorrer o chamado “escoamento” até atingir o ponto de ruptura.
Para ter uma noção da fase do “escoamento”, pode-se pegar uma fita plástica e puxar em ambas as extremidades. Ela irá suportar uma certa tensão e em dado ponto começa a ceder, parecendo que o material “escorre”, ficando mais fina e mais estreita. Ao atingir um certo ponto, parece estabilizar e logo depois rompe abruptamente. Submetendo uma peça de metal a um dispositivo de tração, irá ocorrer a mesma coisa, apenas em níveis diferentes.
Exercícios para resolver
01. Uma mola tem constante elástica $k = {300,0} N/m$. Faça o gráfico $F=f{\Delta L}$.
02. Uma mola de constante elástica igual a $k = {200,0} N/m$ tem comprimento de $ L = 20 cm$. Quando submetido a uma força externa, o comprimento dessa mola passa a ser de 15 cm. Determine o módulo da força elástica que é exercida pela mola nestas condições.
03. Quando comprimida por uma força de 4 N, uma mola tem o seu comprimento alterado em 1,6 cm (0,016 m). Determine o valor da constante elástica dessa mola.
04. Ao ser esticada do seu tamanho original de 10 cm para 15 cm, uma mola exerce uma força elástica de 50 N. Qual é o valor de sua constante elástica?
05. Uma mola helicoidal varia seu comprimento de $L_{0} = {10,0}cm$ para $)_{1} ={22,0} cm$ quando penduramos em sua extremidade um corpo de $P_{1} ={4,0}N$. Determine o comprimento total dessa mola quando penduramos nela um corpo de $P_{2}={6.0}N$.
Havendo dúvidas, pergunte sem receio.
Curitiba, 30 de março de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
