Física – Mecânica
Alavancas
A alavanca é talvez a $\color{Brown){máquina simples}$ mais antiga em uso pela humanidade. Em geral ouvimos falar de Arquimedes, que teria difundido seu uso, mas isso foi a questão de 2300 aos passados e creio que muito antes disso, mesmo sem lhe dar um nome ou descrever em detalhes seu funcionamento, os seres humanos já faziam uso dela em seu dia a dia. É suficiente olhar para as edificações levantadas nessas épocas remotas e que subsistem até hoje, mesmo passando por diversos eventos danosos. Não consigo imaginar fazer tudo isso sem o uso das alavancas.
Basicamente uma alavanca é constituída de uma barra de material sólido e resistente, com um comprimento apropriado. Seu funcionamento baseia-se em um ponto de apoio ou um eixo de rotação. Para nos fornecer vantagem mecânica, ela deve possuir um braço da potência e um braço da resistência. Via de regra estes possuem comprimentos diferentes, dependendo da finalidade que temos em mente.
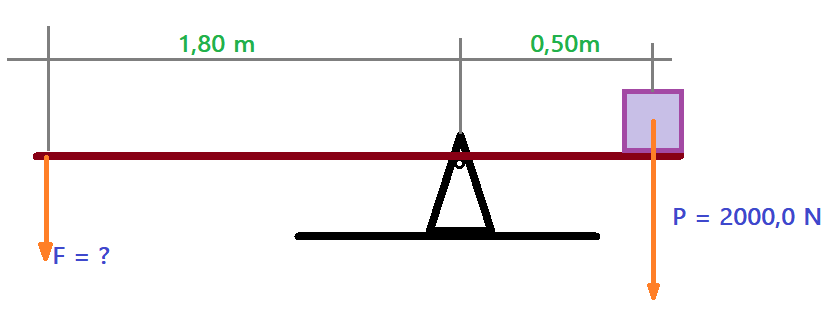
O sentido de rotação depende de uma pequena diferença entre os módulos dos momentos estáticos em relação ao ponto fixo (eixo de rotação). Com a igualdade entre eles, estabelece-se o equilíbrio.
$$\color{Blue}{F_{p}\cdot b_{p} = F{r}\cdot b_{r}}$$
Vantagem mecânica
Denominamos vantagem mecânica o que ganhamos com o uso da “máquina”. Em geral temos em mente mover corpos mais pesados do que a força disponível para tal. A proporção entre os braços da alavanca determina esse ganho de força. Por outro lado, se ganhamos em força, perdemos em deslocamento. No entanto existem soluções para isso. Tomando a igualdade acima, podemos escrever na forma de proporção, que nos fornece a $\color{Blue}{vantagem mecânica}.
$F_{p}\cdot b_{p} = F_{r}\cdot b_{r}$$\Leftrightarrow$$ \frac{b_{p}}{b_{r}} = \frac{F_{r}}{F_{p}}$
$\color{Brown}{V_{m} = \frac{b_{p}}{b_{r}} =\frac {F_{p}}{F_{r}}}$
$\color{Brown}{V_{m}\gt 1}$$\Leftrightarrow$ alavancas interfixa e inter-resistente.
$\color{Brown}{V_{m}\lt 1}$$\Leftrightarrow$ alavanca interpotente.
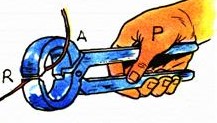
Vejamos algumas imagens de situações em que é aplicado o conceito das alavancas.
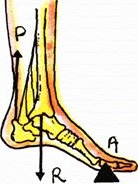
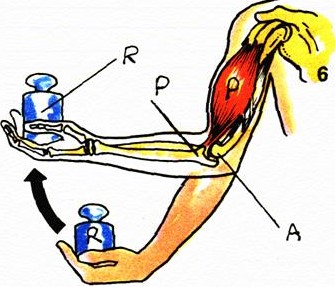
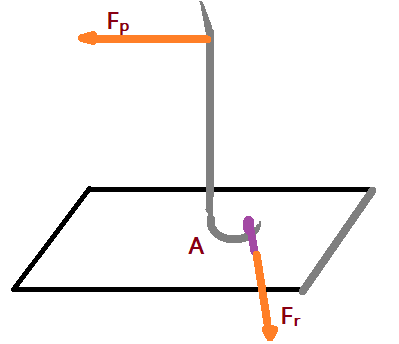
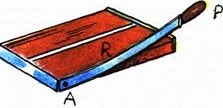
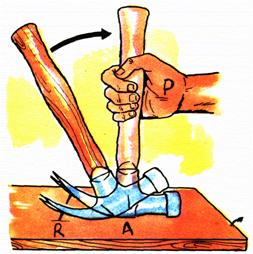



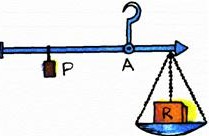
Poderíamos listar uma porção de outros dispositivos mais onde se aplica a noção de alavancas, como por exemplo uma gangorra.
Tipos de alavancas
- Interfixa é a alavanca que tem o ponto de apoio ou eixo de rotação numa posição entre a força da resistência e da potência. É o caso da alavanca usada para introduzir o assunto no início.
- Inter-resistente é uma alavanca onde o ponto de apoio ou eixo de rotação se localiza em uma extremidade, a força da resistência é aplicada em um ponto intermediário e a potência na outra extremidade. É o caso da figura que segue.
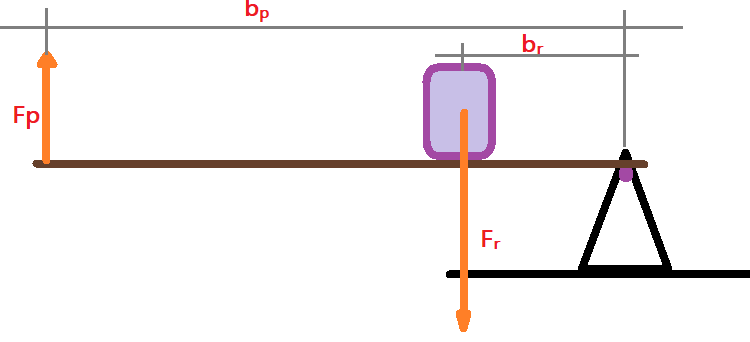
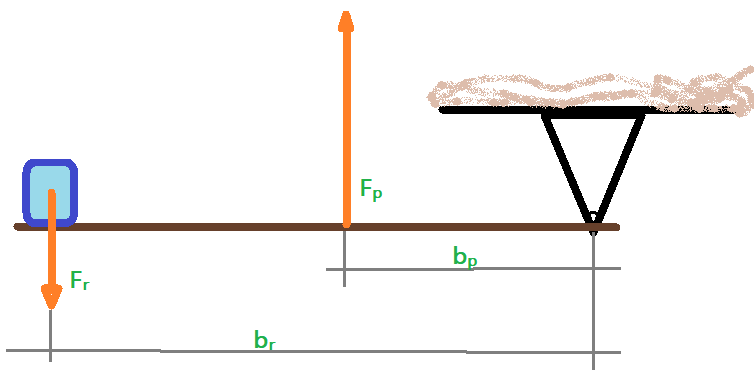
3. Interpotente é a alavanca em que a articulação ou apoio se localiza em uma extremidade, a força resistente esta apoiada na outra extremidade e a potência em um ponto intermediário.
Vamos exercitar
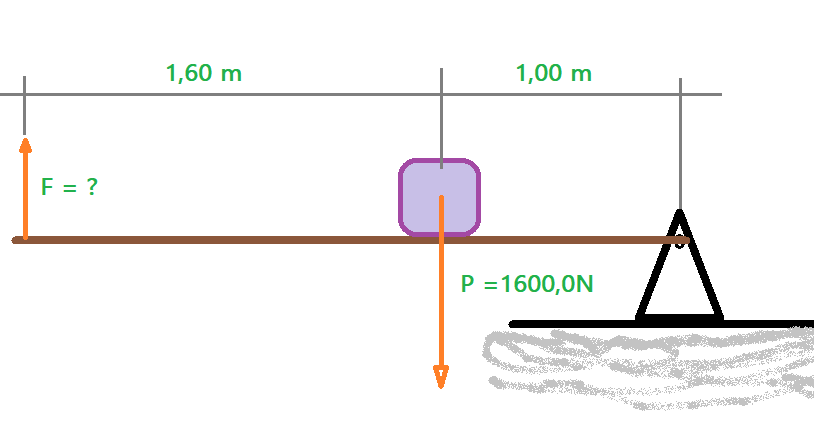
01. Vamos determinar a força da potência na alavanca representada na figura ao lado. Qual é sua vantagem mecânica?
$\color{Brown}{F_{r} = 1600,0 N}$
$\color{Brown}{b_{p} = 1,6 m}$
$\color{Brown}{b{r} = 1,0 m}$
$F_{p}\cdot b_{p} = F_{r}\cdot b_{r}$
$F_{p}\cdot {1,6} = {1600,0}\cdot {1,0}$$\Leftrightarrow$$ F_{p}=\frac{1600,0}{1,6}$
$\color{Blue}{F_{p} = 1000,0 }N$
$V_{m} = \frac{1,6}{1,0} $
$\color{Blue}{V_{m} = 1,6 }$
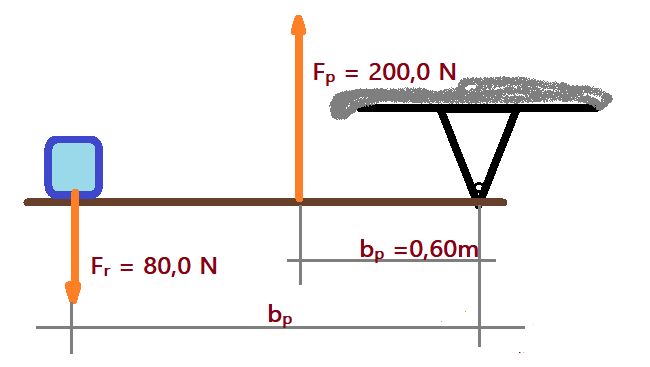
02. Determine o braço da resistência na alavanca da figura e a sua vantagem mecânica.
$F_{p}\cdot b_{p}=F_{r}\cdot b{r}$
${200}\cdot {0,60} = {80,0}\cdot b{r}$$\Leftrightarrow$$ b_{r} = \frac{120,0}{80,0}$
$\color{Blue}{b_{r} = 1,5 m}$
$V_{m} = \frac{0,60}{1,5}$
$\color{Blue}{V_{m} = 0,4}$
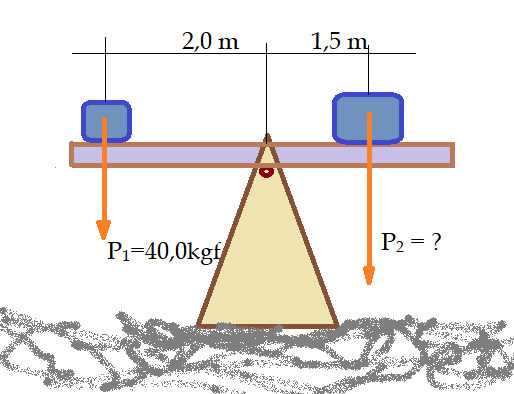
03. Determine a força da potência na alavanca interfixa da figura, além de sua vantagem mecânica.
Em verdade temos aí uma gangorra, que também é uma alavanca interfixa.
$F_{p}\cdot b_{p} = F_{r}\cdot b_{r}$
$F_{p}\cdot {1,5} = {40,0}\cdot {2,0} $
$F_{p} = \frac{80,0}{1,5}$$\Leftrightarrow$$ F_{p} = 53,33 kgf$
$\color{Blue}{F_{p} = 53,33 }$
$V_{m} = \frac{b_{p}}{b_{r}}$$\Leftrightarrow$ V_{m}=\frac{1,5}{2,0}$
$\color{Blue}{V_{m} = 0,75}$
Exercícios para resolver.
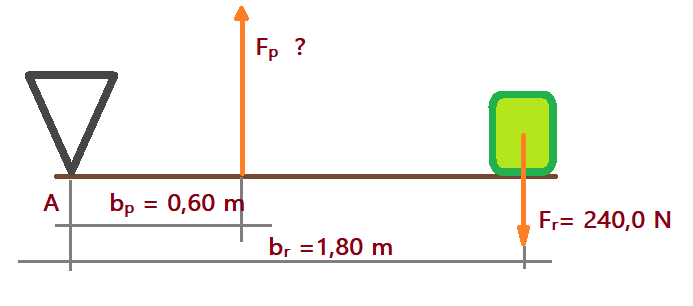
01. Determine a força da potência na alavanca interpotente da figura. Também a vantagem mecânica.
02. Determine a força da potência nas alavancas representadas com as figuras que seguem, bem como a vantagem mecânica que oferecem.
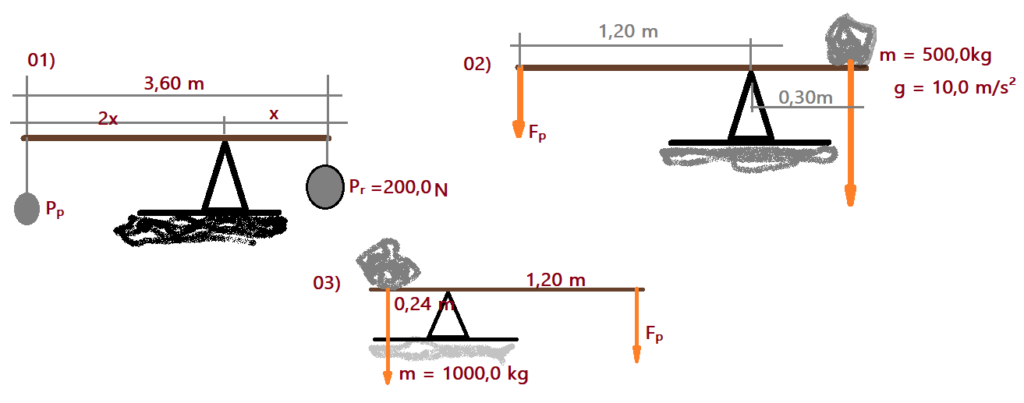
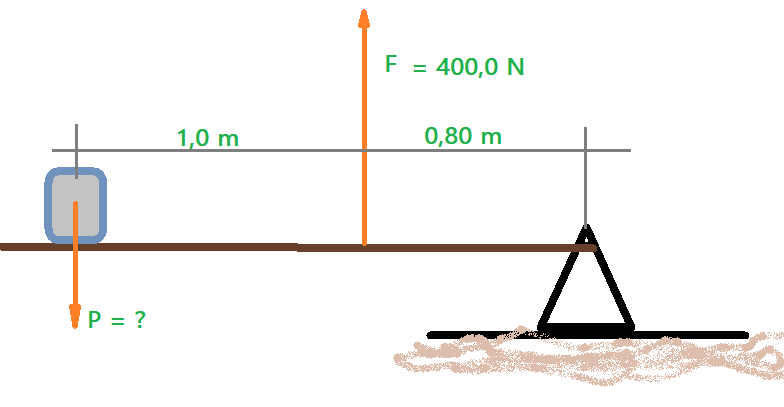
03. Determine a intensidade da força resistente na alavanca interpotente da figura e sua vantagem mecânica.
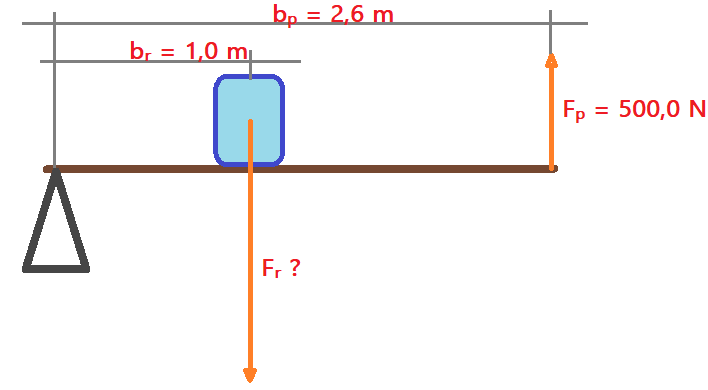
04. Na alavanca representada na figura ao lado, determine a intensidade da força de resistência além de sua vantagem mecânica.
05.
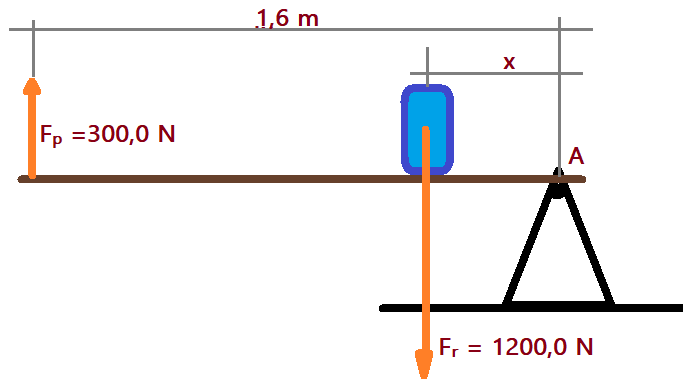
Determine o braço da resistência na alavanca desenhada na figura ao lado e a sua vantagem mecânica.
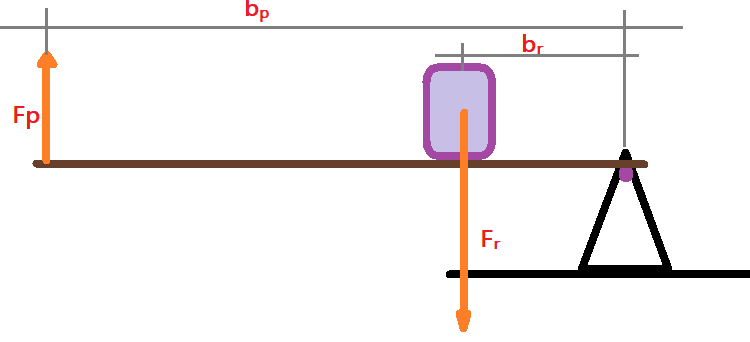
06. Considera os valores $F_{p} = 200,0 N$, $b_{p} = 3,0 m$ e $b_{r} = 0,60 m$, para determinar a vantagem mecânica do dispositivo e o valor da força da resistência.
Se houver dúvidas, consulte-me por um dos canais abaixo.
Curitiba, 27 de março de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
@AdamsDcio
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
