Física – Mecânica – Movimentos planetários.
Leis de Kepler
Depois que Nicolau Copérnico ousou desafiar o “status quo” do geocentrismo, tido como dogma pela Igreja Católica, postulando ser o Sol centro enquanto os planetas giram ao seu redor. Ele escapou das malhas da Inquisição por ser cidadão do leste europeu, onde o poder de Roma tinha pouca influência naquela época. Nicolau Copérnico era de nacionalidade polonesa e nasceu em Torun, no dia 19/02/1473 e faleceu em Frauenburg, a 24/05/1543. Contava ao morrer 70 anos e a causa de sua morte foi um AVC (Acidente Vascular Cerebral).

O sistema geocêntrico descrito por Claudio Ptolomeu, nascido no ano 90 d.C, tendo como base as teorias de Aristóteles, junto com as observações de Hiparco, colocava a Terra como centro do Sistema Solar. O Sol e demais planetas giravam em torno, num complicado sistema de círculos que se moviam em outro círculo maior. Suas trajetórias eram chamadas de epiciclos. Neste círculo maior, próximo do centro ou deferente, localizava-se a Terra. O sistema funcionou tão bem, apesar de suas deficiências científicas, que se sustentou por mais de 1300 anos, quando foi suplantado pelo sistema heliocêntrico de Copérnico.

Outro astrônomo, nasceu com o nome Tyge Ottesen Brahe, em 14/12/1546, no Castelo de Knustorp, na Suécia. Seu pai advogado, era governador de uma região, ocupando uma posição mais honorária que de poder e economicamente pouco rentável. Um tio rico, residente na Dinamarca, tornou-se seu tutor e por isso teve ocasião de estudar em escolas de renome. O tio exigia que se dedicasse ao estudo das leis, que não lhe despertaram grande interesse. Aos 12 anos presenciou um eclipse solar, previsto pelos astrônomos e ficou fascinado com a grandiosidade do evento. Ser capaz de prever sua ocorrência, lhe pareceu um feito extraordinário. Decidiu dedicar seus melhores esforços aos estudos astronômicos. Seria um astrônomo. Assim passou a manter uma dupla jornada de estudos. Uma dedicada às leis e ao Latim em especial. A outra, com sacrifício de seu período de descanso, dedicava ao estudo de astronomia. Quando o tio faleceu e lhe deixou uma herança considerável, pode finalmente dedicar-se ao que realmente queria.
Passou para história com o nome Tycho Brahe, que é a forma latinizada do nome de batismo. O rei da Suécia o subvencionou por cerca de 20 anos, durante os quais pode construir o mais moderno observatório astronômico conhecido como Uranienborg, na ilha de Hveen. Modernizou todos os instrumentos de observação introduzindo importantes aperfeiçoamentos. Assim pode realizar observações extremamente precisas, inclusive aperfeiçoando observações de Copérnico. Algumas de suas tábuas continuam sendo tomadas como referência até os dias de hoje pelos astrônomos modernos.

Mantinha-se longe das polêmicas entre os heliocentristas e geocentristas. Limitava-se a observar e fazer cálculos das órbitas. Isso confirmava a teoria heliocêntrica. Com a morte do rei Frederico, seu protetor, caiu em desgraça e foi destituído da chefia do seu observatório. Refugiou-se em Praga, onde lhe foi concedido um pequeno Castelo e pode continuar com suas observações, em um pequeno observatório. Teve como hóspede Johannes Kepler, que herdou suas observações e foi seu continuador.

Com base nas observações e anotações de Brahe, Kepler realizou os cálculos que o levaram a propor, em duas etapas, as três leis básicas dos movimentos celestes. São elas:
Lei das órbitas: (1609)- Os planetas descrevem órbitas elípticas em torno do Sol, que ocupa um dos focos a elipse. Também é conhecida como Primeira Lei de Kepler.
A soma das distâncias do planeta ao centro do Sol e ao outro foco, é constante e igual à medida do eixo principal ${X”X’}$. A excentricidade da órbita varia entre ${0\le e \le 1}$ sendo calculada pelo quociente entre a distância do foco ao centro da elipse ${c}$ e o semi-eixo maior ${a}$.
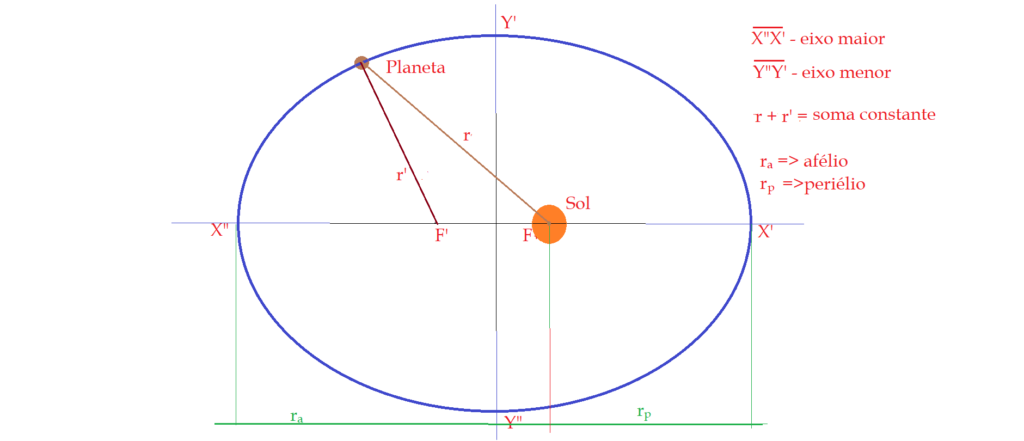
$$\color{Brown}{e =\frac{c}{ a}}$$
Se ${e = 0}$$\Rightarrow$ a órbita é circular.
Se ${0\le e \le 1}$$\Rightarrow$ a órbita é de excentricidade crescente.
Se ${e = 1}$$\Rightarrow$ a órbita é completamente achatada. Seria um movimento oscilatório entre os extremos do eixo principal. Situação extrema.
A excentricidade da Terra equivale a ${e=0,017}$. O planeta com maior excentricidade é Mercúrio, com ${e=0,205}$, e o planeta com menor excentricidade é Vênus com ${e=0,007}$, possuindo uma órbita praticamente circular.
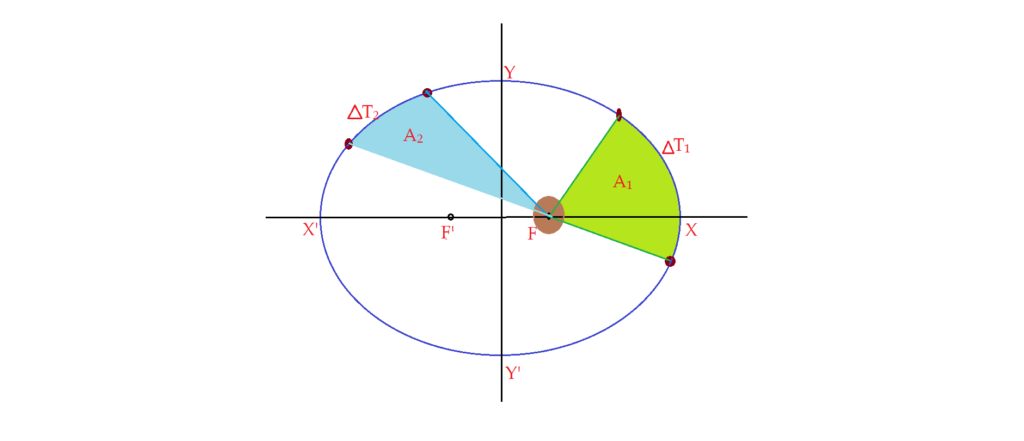
Lei das áreas:(1609) – Para qualquer planeta, o raio vetor, que une o seu centro ao centro do Sol, varre áreas iguais em intervalos de tempo iguais. Observe a figura. Também chamada Segunda Lei de Kepler.
$$\color{Blue}{\frac{A_{1}}{\Delta T_{1}} =\frac{A_{2}}{\Delta T_{2}}}$$
Isso implica em que a velocidade de translação do planeta varia ao longo da sua órbita. Quando a distância é maior, a velocidade é menor.
Lei dos Períodos:(1618) – Para qualquer planeta em órbita em torno de um astro como o Sol, o quadrado do período de translação é proporcional ao cubo do raio médio de sua órbita. Que também é conhecida como Terceira Lei de Kepler.
$$\color{Navy}{\frac{T^{2}}{a^{3}} = K}$$
O valor da constante K é calculado pela expressão:
$$\color{Lime}{K = \frac{4{\pi}^{2}}{GM_{s}}}$$
Isso nos permite determinar por comparação os períodos de planetas e outros astros em órbita.
$$\color{Navy}{\frac{T_{1}^{2}}{a_{1}^{3}} = \frac{T_{2}^{2}}{a_{2}^{3}} = \frac{T_{n}^{2}}{a_{n}^{3}}}$$
Esses conhecimentos são fundamentais nos cálculos que permitem determinar a altura e velocidade de satélites artificiais lançados na órbita da terra, no lançamento de veículos automáticos que demandam outros corpos celestes aos quais irão orbitar com fins de pesquisa.
NOTA: Existe um comentário de que Kepler teria cometido um leve erro nos cálculos feitos para chegar à conclusão correta na Lei dos Períodos. Teria sido exatamente esse engano que o levara ao resultado correto. Os recursos matemáticos disponíveis na época ainda eram limitados e não teriam permitido, tirar tais conclusões com os dados disponíveis. Mas isso é lenda. Nunca vi nada que justificasse essa assertiva. Essa afirmação tem por base o fato de que o cálculo integral, constituído de limites, derivadas e integrais ter surgido posteriormente, com Isaac Newton e Leibnitz. Mas ninguém pode refutar o acerto dos cálculos, uma vez que tudo foi posteriormente comprovado de sobejo.
| Planeta | Raio médio de sua órbita em UA* | Período em anos terrestres | $$\frac{T^2}{R^3}$$ |
| Mercúrio | $$0,387$$ | $$0,241$$ | $$1,002$$ |
| Vênus | $$0,723$$ | $$0,615$$ | $$1,001$$ |
| Terra | $$1,00044 | $$1,000$4 | $$1,000$$ |
| Marte | $$1,524$$ | $$1,881$$ | $$1,000$$ |
| Júpiter | $$5,203$$ | $$11,800$$ | $$0,999$$ |
| Saturno | $$9,539$$ | $$28,469$$ | $$1,000$$ |
| Urano | $$19,190$$ | $$84,010$$ | $$0,999$$ |
| Netuno | $$30,060$$ | $$164,800$$ | $$1,000$$ |
NOTA: Até há alguns anos havia mais um astro que fazia parte do grupo dos planetas. Denominado Plutão. Por ocasião de uma reclassificação de corpos celestes, ele foi incluído no grupo dos asteroides, também chamados de Corpos Intermediários. De fato ele chega a perder em dimensões para alguns astros desse grupo, que circundam num chamado “Cinturão de Asteroides”.
Vamos exercitar
01. (Ita 2019) – Uma estação espacial, denominada Kepler, estuda um exoplaneta, cujo satélite natural tem órbita elíptica, de semieixo maior $a_{0}$ e seu período é $T_{0}$. A distância entre a estação espacial e o exoplaneta é $d = 32a_{0}$. Um objeto se desprende da estação Kepler e é atraído gravitacionalmente pelo exoplaneta, iniciando um movimento de queda livre a partir do repouso em relação a ele. Desprezando a rotação do exoplaneta, a interação gravitacional entre o satélite e o objeto, bem como as dimensões de todos os corpos envolvidos, calcule em função de $T_{0}$ o tempo de queda do objeto.
Resolução: Considerando que a excentricidade da trajetória elíptica que o objeto descreverá é aproximadamente igual a unidade, podemos admitir que o raio da órbita do objeto será igual à metade da distância entre a estação espacial e o exoplaneta. Bastará então calcularmos o tempo de aproximação do objeto em relação ao planeta a partir de sua posição inicial. Para isso necessitamos o período da órbita. O tempo de queda, por sua vez, será igual a metade desse tempo.
$\frac{T_{0}^{2}}{a_{0}^{3}}= \frac{T^{2}}{\left({16a_{0}}\right)^{3}}$
$T^{2} = \frac{T_{0}^{2}}{a_{0}^{3}}\times{\left({16 a_{0}}\right)^{3}}$
Cancelando o fator comum entre numerador e denominador:
$T^{2} = T_{0}^{2}\times 16^{3}$
Decompondo o fator ${16}$ em seus fatores primos temos:
$16 = 2^{4}$$\Leftrightarrow$$T^{2}=T_{0}^{2}\times{\left(2^{4}\right)^3}$
$\sqrt{T^{2}}= \sqrt{T_{0}^{2}\times{2}^{12}}$
$T = T_0\times 2^{6}$
Se o tempo de queda é metade do período, fica:
$t_{q} = \frac{T_{0}\times 2^{6}}{2}$
$$\color{Maroon}{t_{q} = 32\times T_{0}}$$
02. Marte tem dois satélites: Fobos, que se move em órbita circular de raio $R_{F} =10000\, km$ e tem período de translação ${T_F}= 3\times {10}^4\,s$, e Deimos, que tem órbita circular de $R_{D}=24000\,km$. Determine o período de translação de Deimos.
$$\color{Navy}{\frac{T^{2}}{R^{3}} = k}$$
Essa expressão nos vem da 3ªLei de Kepler para os planetas, mas é igualmente válida para satélites e outros astros. Assim podemos escrever para Fobos e Deimos, para determinar o período de translação de Deimos.
$\frac{T_{F}^{2}}{R_{F}^{3}} = k$
$\frac{T_{D}^{2}}{R_{D}^{3}} = k$
Igualando as duas equações:
$\frac{T_{F}^{2}}{R_{F}^{3}} = \frac{T_{D}^{2}}{R_{D}^{3}}$
Isolando $T_{D}^{2}$, teremos:
$T_{D}^{2} = \frac{T_{F}^{2}}{R_{F}^{3}}\times R_{D}^{3}$
$\sqrt{T_{D}^{2}} =\sqrt{\frac{T_{F}^{2}}{R_{F}^{3}}\times R_{D}^{3}}$$
$${T_D}= \sqrt{\frac{\left(3\times{10}^{4}\right)^{2}}{\left(10^4\right)^{3}}\times{\left(2,4\times{10}^{4}\right)^{3}}}$$
Cancelando os fatores comuns entre numerador e denominador teremos:
$T_{D} =\sqrt{9\times{10}^{8}\times {13,824}}$
$$\color{Maroon}{T_{D}= \sqrt{{124,416}\times{10}^{8}} \simeq 1,115\times 10^{5}\, s}$$
03. A Terra descreve uma elipse em torno do sol, cuja área é $A_{12}=6,98\times{10}^{22}\,m^{2}\,$. Qual é a área varrida pelo raio que liga a Terra ao Sol entre $0,0 h$ do dia $1^{0}$ de abril e as $24\, h$ do dia 30 de abril do mesmo ano.
A 2ª Lei de Kepler nos diz que o raio vetor que liga o planeta ao centro do Sol varre áreas iguais em intervalos de tempo iguais.
O período mencionado corresponde a um mês. Um ano tem ao todo 12 meses. Isso nos permite dividir a área total da elipse por 12, obtendo a área correspondente ao período de um mês, compreendido no intervalo descrito no enunciado.
$$\color{Nav}{A_{12} = {6,98}\times{10}^{22}\, m^{2}$$
$A_{1} = \frac{{6,98}\times{10}^{22}}{12}$
$$\color{Maroon}{A_{1} = {5,82}\times{10}^{21}\, m^2}$$
04. Durante qual estação do ano, no hemisfério norte, a Terra possui maior velocidade orbital? Em qual estação ela está com sua menor velocidade orbital? Sabemos que a Terra está no periélio quando é início de janeiro.
Estar no periélio significa estar em sua menor distância com relação ao sol. Isso significa que nesse momento a velocidade orbital atinge seu valor máximo. O hemisfério norte, no começo de janeiro, está em pleno inverno.
Já, o momento de maior distância ao Sol, é o afélio, quando a velocidade orbital do planeta atinge seu valor mais baixo. Isso ocorre em pleno verão no hemisfério norte.
05. Um planeta orbita em torno de um astro massivo. No periélio sua distância ao astro é $R = 1,0\times{10}^{15}\,m$ e sua velocidade orbital é de $v=5,0\times{10}^{4}\,m/s\,$. No afélio sua distância passa a ser de $R=2,2\times{10}^{15}\,m$. Qual é sua velocidade nesse ponto?
Em uma trajetória de grande raio de curvatura, a distância linear percorrida por um corpo, em uma unidade de tempo, pode ser considerada sem cometer um erro significativo, como sendo um segmento de reta e teremos a tarefa de avaliar a área de dois triângulos isósceles, onde os lados são os raios do planeta ao Sol. Para intervalos de tempo suficientemente pequenos, podemos considerar a altura como sendo de mesmo valor que o raio. O pequeno lado, é o deslocamento do planeta: $\Delta x= v\times \Delta t$. Os dois triângulos, de conformidade com a Segunda Lei de Kepler (Áreas), tem a mesma área. Assim:
$A_{1} = A_{2}$
$A_{\Delta} =\frac{b\times h}{2}$
A base de cada triângulo é dada pelo produto da velocidade orbital pelo intervalo de tempo: $b = v_{1}\times\Delta t $ e $h \simeq R$
Então: $\frac{v_{1}\times\Delta t\times R_{1}}{2} = \frac{v_{2}\times\Delta t\times R_{2}}{2}$
Cancelamos os fatores comuns aos dois membros da equação e teremos:
$v_{1}\times R_{1} = v_{2}\times R_{2}$
${5,0}\times{10}^{4}\times{1,0}\times{10}^{15} = v_{2}\times{2,2}\times{10}^{15}$
$v_{2} = \frac{{5,0}\times{10}^{19}}{{2,2}\times{10}^{15}}$
$$\color{Navy}{v_{2} = {\frac{5,0}{2,2}}\times {10}^4\, m/s\simeq {2,27}\times{10}^{4}\,m/s}$$
Exercícios para seu treino.
Ponha em prática o que aprendemos.
01. Um asteroide tem rapidez orbital de $V_{1}=20\,km/s$ quando está em seu periélio e no afélio sua rapidez se reduz para $V_{2}=14,0\,km/s$. Determine a razão entre os raios máximo e mínimo do asteroide e compare a média desses valores com o da Terra, para saber se ele está mais perto ou mais longe do Sol. A distância média da Terra ao Sol é $R= 149,6\times{10}^{6}\,km$.
02. O novo cometa Alex-Casey tem uma órbita acentuadamente excêntrica, cujo período é $T_{Ac}= 127,4 anos$. Se a distância mínima do cometa em relação ao Sol ele se aproxima a $R_{Ac}= 0,1\,UA$. Sabendo que: $G={6,67}\times{10}^{-11}\,Nm^{2}/kg^{2}$; $M_{Terra}= {5,98}\times{10}^{24}\, kg$ e $ 1,0\,UA = 149\times{10}^{9}\,m$, determine a maior distância entre o Alex-Casey e o Sol.
03. A órbita da Terra tem em media $R_{T}={1,496}\times{10}^{11}\,m$. Urano tem o raio médio de sua órbita $R_{U}={2,87}\times{10}^{12}\,m$. Determine o período orbital de Urano, tomando como base um ano terrestre.
04. O asteroide Hector, descoberto em 1907, tem uma órbita circular de raio que mede $R_{H}= 5,16\,UA$. Determine a o período orbital do asteroide Hector.
05. A massa de Saturno é $M_{S}= {5,69}\times{10}^{26}\,kg$. a) Determine o período de sua Lua Mimas, que tem um raio orbital médio é de $R_{M} = 1,86\times{10}^{8}\,m$; b)determine o raio orbital médio de sua Lua Titã, que tem período $T_{T}= {1,38}\times{10}^{6}\,s$.
06. O cometa Halley orbita o Sol em uma órbita acentuadamente excêntrica, cujo período é de aproximadamente 76 anos. Sua última aproximação em relação à Terra e Sol, ocorreu em 1987. Pede-se: a) em que anos ele esteve viajando com maior velocidade durante sua órbita; b) em que ano ele esteve viajando com a sua menor velocidade orbital.
07. (UNIFESP-SP) – A massa da Terra é aproximadamente 80 vezes a massa da Lua e a distância entre os centros de massa desses astros é aproximadamente 60 vezes o raio da Terra. A respeito do sistema Terra-Lua pode-se afirmar que:
( )a) a Lua gira em torno da Terra com órbita elíptica e em um dos focos dessa órbita está o centro de massa da Terra;
( )b)a Lua gira em torno da Terra com órbita circular e o centro de massa da Terra está no centro dessa órbita;
( )c) a Terra e a Lua giram em torno de um ponto comum, o centro de massa do sistema Terra-Lua, localizado no interior da Terra;
( )d) a Terra e a Lua giram em torno de um ponto comum, o cengtro de massa do sistema Terra-Lua, localizado no meio da distância entre os centros de massa da Terra e da Lua;
( )e) a Terra e a Lua giram em torno de um ponto comum, o centro de massa do sistema terra Luz, localizado no interior da Lua.
08. (MACKENZIE-SP) – De acordo com uma das Leis de Kepler, o raio vetor que une o centro do planeta ao centro do Sol, varre áreas iguais em intervalos de tempo iguais em torno do Sol. Como as órbitas são elípticas e o Sol ocupa um dos focos, conclui-se que:
I)Quando o planeta está mais próximo do Sol, sua velocidade aumenta;
II) Quando o planeta está mais distante do Sol, sua velocidade aumenta;
III)- A velocidade do planeta em sua órbita elíptica independe de sua posição relativa ao Sol.
Responda de acordo com o código a seguir:
( )a) somente I é correta;
( )b) somente II é correta;
( )c) somente II e III são corretas;
( )d) todas estão corretas;
( )e) nenhuma é correta;
09. (UFSC) – Sobre as Leis de Kepler, assinale as proposições verdadeiras para o sistema solar.
01 – O valor da velocidade de revolução da Terra, em torno do Sol, quando sua trajetória está mais próxima do Sol, é maior do que quando está mais afastado do mesmo;
02 – Os planetas mais afastados do Sol têm um período de revolução, em torno do mesmo, maior que os mais próximos;
04 – Os planetas de maior massa leva mais tempo para dar uma volta em torno do Sol, devido à sua inércia;
08 – O Sol está situado num dos focos da órbita elíptica de um dado planeta;
16 -Quanto maior for o período de rotação de um dado planeta, maior será seu período de revolução em torno do Sol;
32 – No caso especial da Terra, a órbita é exatamente uma circunferência.
Dê como resposta a soma dos números que precedem as proposições corretas.
10. (UNISINOS-RS) – Durante o primeiro semestre deste ano, foi possível observar o planeta Vênus bem brilhante, ao anoitecer.
Sabe-se que Vênus está bem mais perto do Sol que a Terra. Comparados com a Terra, o período de translação de Vênus em torno do Sol é …………………e sua velocidade orbital é…………………..As lacunas são corretamente preenchidas, respectivamente, por:
( )a) menor; menor;
( )b) menor; igual;
( )c) maior; menor;
( )d) maior; maior;
( )e) menor; maior.
11. (ENEM)- As Leis de Kepler definem o movimento dos planetas em torno do Sol. Qual é, aproximadamente o tempo gasto, em meses, pela Terra para percorrer uma área igual a um quarto da área total da elipse?
( )a) 9; ( )b) 6; ( )c) 4; ( )d) 3; ( )e) 1.
12. ( MACKENZIE-SP)- Dois satélites de um planeta tem períodos de translação de 32 dias e 256 dias, respectivamente. Se o raio de órbita do primeiro satélite vale 1(uma) unidade, então o raio de órbita do segundo terá quantas unidades?
13. (UEPB) – O astrônomo alemão Johannes Kepler(1571-1630), adepto do sistema heliocêntrico, desenvolveu um trabalho de grande vulto, aperfeiçoando as idéias de Nicolau Copérnico. Em consequência ele conseguiu estabelecer três leis sobre o movimento dos planetas, que permitiram um grande avanço no estudo da astronomia. Um estudante ao ter tomado conhecimento das Leis de Kepler concluiu, segundo as proposições a seguir, que:
I. Para a primeira Lei de Kepler (Lei das Órbitas), o verão ocorre quando a Terra está mais próxima do Sol, e o inverno, quando ela está mais afastada;
II. Para a segunda Lei de Kepler (Lei das Áreas), a velocidade de um planeta X, em sua órbita, diminui à medida que ele se afasta do Sol;
III. Para a terceira Lei de Kepler (Lei dos Períodos), o período de rotação de um planeta em torno de seu eixo, é tanto maior quanto maior for seu período de revolução.
Com base na análise feita, assinale a alternativa correta:
( )a) apenas as proposições II e III são verdadeiras;
( )b) apenas as proposições I e II são corretas;
( )c) apenas a proposição II é verdadeira;
( )d) apenas a proposição I é verdadeira;
( )e) todas as proposições são verdadeiras.
14. (UFRGS-RS) – O ano de 2009 foi proclamado pela UNESCO como o Ano Internacional da Astronomia, visando comemorar os 400 anos das primeiras observações astronômicas realizadas por Galileu Galillei usando instrumentos como telescópios e os 400 anos da promulgação das duas primeiras Leis de Kepler: 1ª Lei das Órbitas e 2ª Lei das Áreas. A 3ª Lei dos Períodos foi promulgada apenas em 1618. Além disso continha o desejo de celebrar a Astronomia e suas contribuições para o conhecimento humano.
Sobre as três leis de Kepler são feitas as seguintes afirmações:
I. A órbita de cada planeta é uma elipse com o sol em um dos focos da mesma.*
II. O segmento de reta (raio vetor) que une cada planeta ao Sol, varre áreas iguais em intervalos de tempo iguais.
III. O quadrado do período orbital de cada planeta é diretamente proporcional ao cubo da distância média do planeta ao Sol.
Quais afirmações são corretas?
( )a) Apenas I;
( )b) Apenas II;
( )c) Apenas III;
( )d) Apenas I e II;
( )e) I, II e III.
15. (UFRGS-RS) – A Astronomia estuda objetos celestes que, em sua maioria, se encontram a grandes distâncias da Terra. De acordo com a mecânica newtoniana, os movimentos desses objetos obedecem à Lei da Gravitação Universal. Considere as seguintes afirmações, referentes às unidades empregadas em estudos astronômicos.
I – Um ano-luz corresponde à distância percorrida pela luz em um ano;
II – Uma Unidade Astronômica (1UA), corresponde à distância média entre a Terra e o Sol;
III – No Sistema Internacional (SI), a unidade da constante G (constante de Gravitação Universal), usada na fórmula da Lei de Gravitação é $m/s^{2}$.
Quais afirmações são corretas?
( )a) Apenas I;
( )b) Apenas II;
( )c) Apenas III;
( )d) Apenas I e II;
( )e) I, II e III.
16. (UEPG-PR) – Durante mais de um milênio e meio, a humanidade aceitou a Teoria Geocêntrica, isto é, a Terra era o centro do Universo. Graças ao trabalho de grandes cientistas, entre eles Johannes Kepler, estabeleceu-se a verdade em relação ao Sistema Solar. A Teoria Heliocêntrica, isto é, o Sol é o centro do sistema e os planetas giram ao seu redor. Com relação às leis enunciadas por Kepler, assinale a alternativa correta.
( )a)Um planeta em órbita em torno do Sol não se move com velocidade constante, mas de tal maneira que uma linha traçada do planeta ao Sol varre áreas iguais em intervalos de tempo iguais;
( )b) Todos os planetas do Sistema Solar, incluindo a Terra, giram em torno do Sol em órbitas circulares, tendo o Sol como centro;
( )c) Periélio é a aproximação entre os planetas e o Sol, enquanto que o afélio é o afastamento entre os planetas e o Sol. No inverno ocorre o periélio;
( )d) A segunda Lei de Kepler prova que a maior velocidade de translação dos planetas no periélio é menor que nos pontos mais afastados no afélio;
( )e) As leis enunciadas por Kepler são válidas apenas para o nosso Sistema Solar.
17. (UERJ) – Adotando o Sol como referencial, aponte a alternativa que condiz com a 1ª Lei de Kepler dos movimentos planetários.
( )a) As órbitas planetárias são curvas quaisquer, desde que fechadas;
( )b) As órbitas planetárias são espiraladas;
( )c) As órbitas planetárias não podem ser circulares;
( )d) As órbitas planetárias são elípticas, com o Sol ocupando o centro da elipse;
( )e) As órbitas planetárias são elípticas, com o Sol ocupando um dos focos da elipse.
18. (Unisa-SP) – A Segunda Lei de Kepler permite concluir que um planeta possui:
( )a) maior velocidade, quando se encontra mais longe do Sol;
( )b) maior velocidade, quando se encontra mais perto do Sol;
( )c) menor velocidade, quando se encontra mais perto do Sol;
( )d) velocidade constante em toda sua trajetória;
( )e) velocidade orbital variável.
19. (UFSM-RS) – Dois planetas A e B do Sistema Solar giram em torno do Sol com períodos de movimento $T_{A}$ e $T_{B}$. Os raios de suas órbitas são respectivamente $8R$ e $R$. Com base nas Leis de Kepler, é CORRETO afirmar que a razão entre $\frac{T_{A}}{T_{B}}$, é dada por:
( )a) $2$; ( )b)$\frac{1}{8}$; ( )c)$4$ ( )d) $\frac{1}{4}$ ( )e) $8$.
20. (UEM-PR-2007) – Dois satélites, A e B estão em órbitas circulares em torno da Terra e a massa de A é $m_{A}\gt m_{B}$. É CORRETO afirmar que:
( )a) os períodos de translação dos satélites são iguais e independem dos raios das órbitas;
( )b) o módulo da velocidade orbital de A é maior que o módulo da velocidade orbital de B quando os raios das órbitas forem iguais;
( )c) as velocidades angulares dos dois satélites são diferentes quando os raios das órbitas forem iguais;
( )d) o módulo das velocidades orbitais dos satélites são iguais para órbitas de mesmo raio;
( )e) a força centrípeta que atua sobre o satélite só depende do raio da órbita.
21. (CESGRANRIO) O raio médio da órbita de marte em torno do Sol é aproximadamente quatro vezes maior do que o raio médio da órbita de Mercúrio em torno do Sol. Assim, a razão entre os períodos de translação $T_{1}$ e $T_{2}$ de Marte e Mercúrio respectivamente, vale aproximadamente:
( )a)$\frac{T_{1}}{T_{2}} = \frac{1}{4}$;
( )b) $\frac{T_{1}}{T_{2}} = \frac{1}{2}$;
( )c) $\frac{T_{1}}{T_{2}} = \frac{2}{1}$;
( )d)$\frac{T_{1}}{T_{2}} = \frac{4}{1}$;
( )e) $\frac{T_{1}}{t_{2}} = \frac{8}{1}$.
22. (FUVEST-SP) – Considere um satélite artificial em órbita circular. Duplicando a massa do satélite sem alterar o seu período de translação, o raio da órbita será:
( )a) duplicado; ( )b) quadruplicado; ( )c) reduzido à metade;
( )d) reduzido à quarta parte;
( )e) permanecerá o mesmo.
22. (UNIFAP-2006) – Analise as assertivas a seguir:
I. O cubo do período orbital de qualquer planeta é proporcional ao quadrado do semieixo maior da órbita elíptica ao redor do Sol.
II. O raio vetor traçado do Sol até qualquer planeta, descreve áreas iguais em intervalos de tempo iguais;
III. Todo planeta, no Sistema Solar, descreve uma órbita elíptica com o Sol no centro da elipse;
IV. A 3ª Lei de Kepler afirma que a força gravitacional de repulsão entre duas paertículas quaisquer varia com o inverso do quadrado da distância entre essas partículas.
Qual(is) a(s) assertiva(s) INCORRETA(S)?
( )a) Apenas IV; ( )b) Apenas II; ( )c) Apenas I, III e IV; ( )d)Apenas II,III e IV. ( )e) I,II,III e IV.
Havendo dificuldades na resolução dos exercícios, faça contato por meio de um dos canais listados abaixo. Estou à disposição para elucidar quaisquer dúvidas.
Curitiba, 31 de janeiro de 2020
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
