Física – Termologia – Calorimetria
No post anterior já falamos das unidades de quantidade de calor. Vamos agora dedicar este post ao estudo dessas quantidades, de seus efeitos e modificações consequentes.
Começaremos por conhecer grandezas que se referem à matéria, à massa e variação de temperatura com certa quantidade de calor.
Calor
Calor é a forma de energia em trânsito entre dois pontos de um corpo ou meio material, que se encontrem em temperaturas diferentes.
As trocas de energia térmica podem ocorrer entre dois pontos de um corpo, entre dois corpos ou mais, podendo estar em contato ou distantes. A transmissão ocorre sempre do ponto ou do corpo mais quente para o menos quente.
Como podemos avaliar a energia que se deslocou?
Capacidade térmica é obtida dividindo-se a quantidade de calor transmitida a um corpo ou por ele cedida, pela consequente variação de temperatura. É própria de um corpo.
$C = {Q\over\Delta\theta}$
Unidades:
$cal/ºC$; $kcal/ºC$; $J/ºC$; $kJ/ºC$
$cal/ºF$; $kcal/ºF$; $J/ºF$; $kJ/ºF$
Escrevendo a equação de forma linear
$Q = C\cdot\Delta\theta$
Calor específico é o quociente entre a quantidade de calor transmitida e o produto da massa pela variação de temperatura. É própria da matéria que compõe um corpo.
$c = {Q\over{m\cdot\Delta\theta}}$
Unidades
$cal/gºC$; $kcal/gºC$; $kcal/kgºC$; $J/gºC$; $J/kgºC$; $kJ/kgºC$
$cal/gºF$; $kcal/gºF$; $kcal/kgºF$; $J/gºF$; $J/kgºF$; $kJ/kgºF$
Da expressão que define o calor específico, podemos obter a
Equação geral da calorimetria.
$Q = m\cdot c\cdot\Delta\theta$
Comparando as equações, vemos que elas se combinam:
$Q = m\cdot c\cdot \Delta\theta$
$Q = \underbrace{m\cdot c}\cdot\Delta\theta$
${Q\over\Delta\theta} = m\cdot c$
Disso resulta que
$C = m\cdot c$
A capacidade térmica de um corpo homogêneo é igual ao produto de sua massa pelo calor específico da substância de que é feito.
Tabela de Calor Específico de Várias Substâncias.
| Substância | Valor em cal/gºC |
| água | 1,000 |
| álcool | 0,600 |
| alumínio | 0,220 |
| ar | 0,240 |
| carbono | 0,120 |
| chumbo | 0,031 |
| cobre | 0,091 |
| ferro | 0,119 |
| gelo | 0,500 |
| hélio | 1,250 |
| nitrogênio | 3,400 |
| latão | 0,092 |
| madeira | 0,420 |
| mercúrio | 0,033 |
| nitrogênio | 0,250 |
| ouro | 0,032 |
| oxigênio | 0,220 |
| prata | 0,056 |
| rochas | 0,210 |
| vidro | 0,160 |
Quando o corpo absorve calor fornecido por uma fonte, o processo é denominado endotérmico. Quando o corpo perde calor para outros corpos ou para o meio circundante, o processo é exotérmico.
Endotérmico é o processo que provoca elevação de temperatura ou mudança de estado físico para uma forma de menor coesão molecular.
Exotérmico é o processo que provoca queda de temperatura ou mudança de estado físico para uma agregação de maior coesão molecular.
Dependendo da transformação que o calor recebido ou perdido provoca, recebe a denominação de calor sensível e calor latente.
Calor sensível é a quantidade de calor absorvida ou cedida por um corpo com variação de temperatura.
Calor latente é a quantidade de calor absorvida ou cedida por um a porção de matéria ao sofrer mudança de estado físico.
Mudança de estado físico
Todas as substâncias podem apresentar-se nos três estados físicos básicos:sólido, líquido e gasoso.
Fusão $\Rightarrow$ passagem do estado sólido para o líquido. Endotérmica.
Vaporização $\Rightarrow$ passagem do estado líquido para o gasoso. Endotérmica.
Sublimação $\Rightarrow$ passagem direta do estado sólido para o gasoso ou vice-versa. Pode ser endotérmica ou exotérmica.
Condensação $\Rightarrow$ passagem do estado gasoso para o líquido. Exotérmica.
Solidificação $\Rightarrow$ passagem do estado líquido para o sólido. Exotérmica.
Obs.: Há os estados intermediários, principalmente o pastoso no processo de fusão.
$ L = {Q\over m}$
$Q= m\cdot L$
Unidades: $cal/g$; $kcal/kg$; $J/kg$; $kJ/kg$
Obs.: Vamos lembrar que $1 cal \simeq 4,186\, J$
Equilíbrio térmico
Dois ou mais corpos ou mesmo partes diferentes de um mesmo corpo estão em equilíbrio térmico quando suas temperaturas são iguais. Este equilíbrio térmico é atingido pela transferência de calor (energia térmica) do corpo ou ponto mais quente para o menos quente, isto é, da temperatura mais elevada para a mais baixa.
Princípio das trocas de calor:
Vários corpos ou porções de materiais diferentes próximos ou em contado uns com os outros, estando à temperaturas diferentes, iniciam um processo de trocas de calor, visando atingir o equilíbrio térmico. Ao término desse processo podemos afirmar que:
A soma das quantidades de calor recebidas é igual às quantidades de calor perdidas por corpos inicialmente à temperaturas diferentes.
$\sum{Q_{r}} +\sum{Q_{p}}= 0$
Para realizar uma experiência de equilíbrio térmico entre vários corpos ou porções de matéria, necessitamos dispor de um Vaso Adiabático. É um recipiente termicamente isolado que impede a troca de calor entre o interior e o exterior. Um exemplo dessa espécie de recipiente é uma garrafa térmica. Cabe lembrar que o vaso adiabático perfeito não existe, mas os que dispomos permitem realizar experimentos com boa aproximação, uma vez que o processo não é de longa duração.
Podemos fazer umas aplicações do que foi visto até aqui.
- Um corpo de massa $m = 5,0 kg$ está à temperatura de $\theta_{0} = 25ºC$. Se a sua capacidade térmica é $C = 6,5\cdot{10}^3 J/ºC$, qual será a sua temperatura final, após receber de modo equilibrado $Q = 4,55\cdot{10}^4 J$ de calor de uma fonte constante. Qual é o calor específico da substância de que o corpo é feito?
Dados: $m= 5,0 kg$
$\theta_{0} = 25ºC$
$Q = 4,55\cdot{10}^4 J$
$C = 6,5\cdot{10}^3 J/ºC$
Podemos estabelecer que $\Delta\theta = \theta – \theta_{0}$
$Q =C\cdot\Delta\theta$$\Leftrightarrow$$ {4,55}\cdot{10}^4 = {6,5}\cdot{10}^3\cdot{(\theta – \theta_{0})}$
${{{4,55}\cdot{10}^4\over {6,5}\cdot{10}^3}} = {\theta – 25ºC}$
${{45,5}\over{6,5}} + 25ºC = \theta$
$\theta = 7 + 25 = 32ºC$
$C = {m\cdot c}$$\Leftrightarrow$$c = {C\over m}$
$c = {{6,5}\cdot{10}^3\over{5}}$$\Leftrightarrow$$ c = 1,3\cdot{10}^3 J/kgºC$
2. Temos um bloco de gelo com $m = 500g$, que se encontra a uma temperatura $\theta_{0} = -15ºC$. A pressão atmosférica é normal e a temperatura de fusão é $\theta_{f}= 0ºC$. O calor latente de fusão do gelo é $L_{f} = 80cal/g$, o calor específico $c_{gelo} = 0,5 cal/gºC$; o calor específico da água é $c_{H_{2}O} = 1 cal/gºC$; o calor latente de vaporização é ${L_{v} = 540cal/g}$; o calor específico do vapor $c_{v} = 0,5cal/gºC$. Qual é a quantidade de calor que é necessário fornecer para transformar o gelo em vapor à temperatura de ${\theta_{v}= 120ºC}$. O ponto de vaporização é igual a ${\theta_{v}= 100ºC}$
Temos três porções de calor sensível e duas de calor latente. Precisamos calcular independentemente e depois fazer a adição de todas as parcelas.
$Q_{1} = {m\cdot c_{gelo}\cdot\Delta\theta_{1}}$
$Q_{1} = {{500,0}\cdot{0,5}\cdot{15}}$$\Leftrightarrow$$Q_{1}=3750 cal$
$Q_{2} = L_{f}\cdot m$
$Q_{2} = {{80}\cdot {500}}$$\Leftrightarrow$$ Q_{2} = 40000 cal$
$Q_{3} ={m\cdot c_{H_{2}O}\cdot(\theta_{v} – \theta_{g})}$S
$Q_{3}= {500}\cdot 1\cdot{100 – 0} = 50000 cal$
$Q_{4}= {m\cdot L_{v}}$$\Leftrightarrow$$Q_{4}= {500}\cdot{540}$
$Q_{4} = 270000 cal$
$Q_{5} = m\cdot c_{v}\cdot{(\theta_{f} – \theta_{v})}$
$Q_{5} = {500}\cdot{0,5}\cdot{(120 – 100)}$$\Leftrightarrow$$Q_{5}={250}\cdot{20}$
$Q_{5} = 5000 cal$
$Q = Q_{1} + Q_{2} + Q_{3} + Q_{4} + Q_{5}$
$Q = 3750 + 40000 + 50000 + 270000 + 5000 = 368750 cal$
Podemos representar isso num gráfico de $\theta = f(Q)$
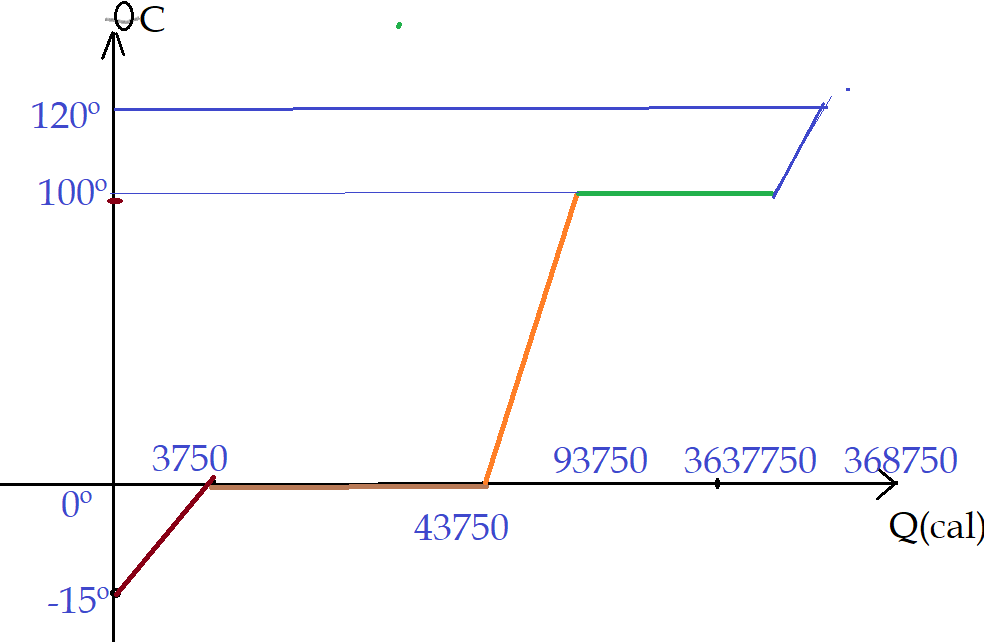
Até o ponto de fusão, gastamos 3750 cal, no processo de fusão, são necessárias 40000 cal, no aquecimento até a ebulição são 50000 cal, na vaporização 270000 cal e no aquecimento do vapor são mais 5000 cal. O total é de 368750 cal.
3. Um paralelepípedo, mede $c = 20,0 cm$, $h= 8,0 cm$ e $l = 10,0 cm$. Sendo o calor específico $c = 0,31 cal/gºC$ e a massa específica $\mu = 3,2 g/cm³$. A temperatura ambiente ele está com $\theta_{1} = 20ºC$. Colocado em contato com uma fonte térmica, absorve calor até atingir a temperatura $\theta_{2} = 80ºC$. Qual é a quantidade de calor absorvida por esse paralelepípedo? Qual é sua capacidade térmica?
$V = c\cdot h\cdot l$$\Leftrightarrow$$V = {20,0}\cdot{8,0}\cdot{10,0}$
$V = 1600,0 cm³$
$\mu = {m\over V}$$\Leftrightarrow$$m = \mu\cdot {V}$
$m = {3,2}\cdot{1600,0}$$\Leftrightarrow$$ m = 5120,0cm³$
$Q = m\cdot c\cdot{(\theta_{2} – \theta_{1})}$
$Q = {5120,0}\cdot{0,31}\cdot{80 – 20}$$\Leftrightarrow$$Q= 95232,0cal$
$C = m\cdot{c}$$\Leftrightarrow$$C = {5120,0} \cdot{0,31} = 1587,2 cal/ºC$
4. Em um vaso adiabático, temos $m_{água} = 300 g$. O vaso tem capacidade térmica $C = 50 cal/ºC$. O calor específico da água é $c_{água}= 1cal/gºC$. O vaso adiabático(calorímetro) está em equilíbrio térmico com a água a $\theta_{1} = 15ºC$. Coloca-se em seu interior um cubo de gelo $c_{gelo}= 0,5 cal/gºC$e massa $m_{gelo}= 50 g$, à $\theta_{gelo}= -25ºC$. O calor de fusão do gelo é $L_{f} = 80 cal/g$. Determinar a temperatura de equilíbrio térmico.
Analisando os dados do problema, vemos que o gelo colocado no calorímetro, irá aquecer até $0ºC$, fundir e depois aquecer até a temperatura de equilíbrio. O calorímetro e a água nele contida irão variar a temperatura até a temperatura de equilíbrio. Então:
${m_{g}\cdot c_{g}\cdot{[0 – (-25)]}}+ {m_{g}\cdot L_{f}} + {m\cdot c_{água}\cdot {theta_{e} – 0}} +{C_{c}\cdot{\theta_{e} – \theta_{1}}}+{m_{água}\cdot c_{água}\cdot{\theta_{e}- \theta_{1}}}= 0$
${{50}\cdot{0,5}\cdot{25} + {50}\cdot{80} + {50}\cdot{1}\cdot{(\theta_{e} – 0)} + {50}\cdot{(\theta_{e}- {15})} + {300}\cdot{1}\cdot{(\theta_{e} -{15})}}$
$625 + 4000 + 50\cdot{\theta_{e}}+ 50\theta_{e} – 750 + 300\theta_{e} – 4500 = 0$
$(50+50 + 300)\cdot\theta_{e} + (4625 – 5250) = 0$
${400}\cdot\theta_{e} – 625 = 0 $
$\theta_{e} ={{625}\over{400}} = 1,562ºC$
Exercícios para resolver.
01 – (PUC-RJ) Uma quantidade de água líquida de massa m = 200 g, a uma temperatura de 30 ºC, é colocada em um calorímetro junto a 150 g de gelo a 0 ºC. Após atingir o equilíbrio, dado que o calor específico da água é c = 1,0 cal/(g . ºC) e o calor latente de fusão do gelo é L = 80 cal/g, calcule a temperatura final nessa situação. Considere a capacidade térmica do calorímetro desprezível.
02 – Em uma panela foram colocados 1,5 kg de água em temperatura ambiente (20 ºC). Ao ser aquecida, sua temperatura passa para 85 ºC. Considerando que o calor específico da água é de 1 cal/g ºC, calcule:
a) a quantidade de calor recebida pela água para atingir essa temperatura;
b) a capacidade térmica dessa porção de água;
03 – Qual a quantidade de calor necessária para que um bloco de 600 kg de gelo, a 0 ºC, se transforme em água nessa mesma temperatura. Considere que o calor latente de fusão do gelo é de 80 cal/g.
04 – Qual a quantidade de calor sensível necessária para aquecer uma barra de ferro de 2kg de 20°C para 200 °C? Dado: calor específico do ferro = 0,119cal/g°C.
05 – Suponha que 50 gramas de gelo a -10 ºC são misturados com 200 gramas de água a 50 ºC dentro de uma garrafa térmica. Qual será a temperatura de equilíbrio do sistema?
Dados:
- calor específico da água: 1 cal/gºC;
- calor específico do gelo: 0,5 cal/gºC;
- calor de fusão do gelo: 80 cal/g.
06 – Aquecedores solares usados em residências têm o objetivo de elevar a temperatura da água até 70 °C. No entanto, a temperatura ideal da água para um banho é de 30 °C. Por isso, deve-se misturar a água aquecida com a água à temperatura ambiente de um outro reservatório, que se encontra a 25 °C. Qual a razão entre a massa de água quente e a massa de água fria na mistura para um banho à temperatura ideal?
- A – 0,111.
- B – 0,125.
- C – 0,357.
- D – 0,428.
- E – 0,833.
07 – Um calorímetro tem capacidade térmica de $C =100cal/ºC$. Coloca-se em seu interior $m_{água}= 1000g$. Quando o equilíbrio térmico é estabelecido afere-se a temperatura que é $\theta_{1} = 20ºC$. Um pedaço de ferro de $m_{f_{e}}= 200 g$, aquecido a temperatura $\theta_{f_{e}} = 300ºC$, é colocado em seu interior e fecha-se o calorímetro. Um termômetro indica a temperatura. Quando o equilíbrio se estabelece, qual será a leitura nesse termômetro? Sabe-se que o $c_{F_{e}} = 0,119 cal\gºC.
08 – Colocamos em um vaso adiabático, de capacidade térmica $C = 60cal/ºC$, inicialmente à temperatura $\theta_{C}= 15ºC$, uma porção de $m_{água}= 500 g$, na temperatura de $\theta_{água}= 30ºC$. Imediatamente acrescentamos uma porção de gelo $m_{gelo}= 120g$, na temperatura de $\theta_{gelo}= -10ºC$. O ponto de fusão do gelo é $\theta_{f} = 0ºC$ e $L_{fg} = 80 cal/g$. Determinar a temperatura de equilíbrio térmico da mistura.
09 – Em um ambiente isolado, colocam-se em contato uma bola de ferro cuja massa é $m_{F_{e}}= 8,0 kg$, a temperatura $\theta_{F_{e}}= 500ºC$, sendo o calor específico do ferro $c_{F_{e}}=0,119 cal\gºC; uma bola de chumbo de massa $m_{P_{b}} = 20,0 kg, na temperatura inicial de $\theta_{P_{b}}= 275°C, sendo o calor específico desse metal $c_{P_{b}}= 0,031cal/gºC$, junto com um cubo de gelo na temperatura de fusão ${\theta_{fg} = 0ºC$, de massa igual a $m_{g}= 3,0 kg$, tudo imerso em $m_{água}= 30,0 kg$ água a $\theta_{água}= 15ºC. Determine a temperatura de equilíbrio térmico.
Havendo dúvidas, peça ajuda sem demora. Estou aqui a disposição.
Curitiba, 04 de novembro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
