Física – Ótica Geométrica – Refração
O que é refração?
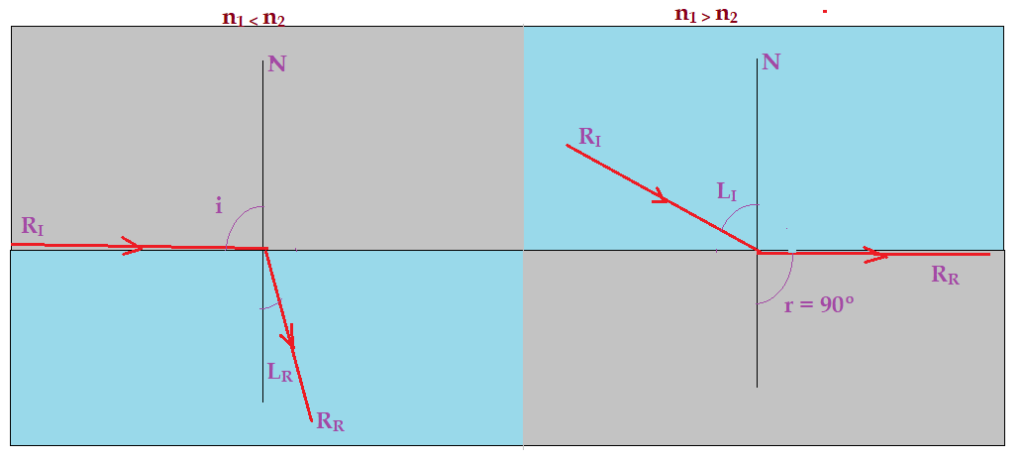
A luz em seu movimento de propagação atravessa diferentes meios transparentes. A natureza do meio determina uma variação na velocidade de propagação. Essa variação de velocidade, produz uma mudança de direção de propagação, sempre que a incidência na superfície de separação (dioptro) entre os dois meios seja diferente de $\color{Maroon}{0^{0}}$ com relação à reta normal no ponto de incidência. Vejamos as figuras.
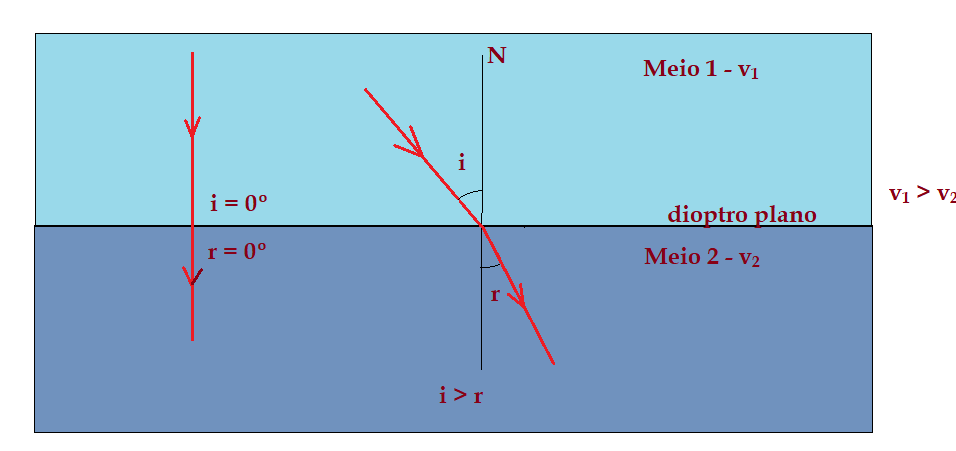
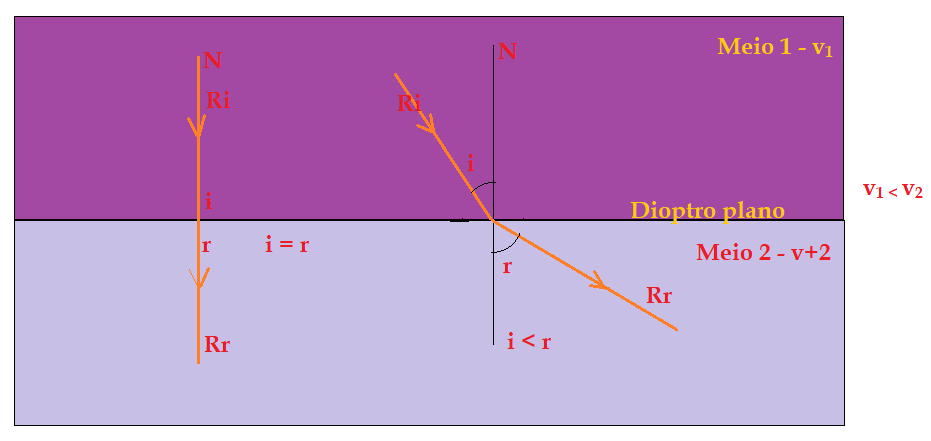
Índice de refração
Denomina-se índice de refração à razão entre a velocidade da luz no vácuo representada por $\color{Maroon}{c}$ e a velocidade da luz no meio para o qual ela está passando. Usamos a letra $\color{Maroon}{n}$ para simbolizar o índice. Assim:
$\color{Navy}{n = \frac{c}{v}}$$\Leftrightarrow$$\color{Blue}{c = v\cdot n}$
Esse é o índice de refração absoluto do meio em relação ao vácuo. Para realizar na prática esse experimento existe o inconveniente de ser necessário ter um equipamento onde possa ser produzido um espaço em que exista vácuo. Por isso, habitualmente trabalhamos com os índices de refração relativos. Podemos considerar o índice absoluto do ar, com razoável aproximação, igual à $\color{Maroon}{n_{ar} = 1}$, pois o erro cometido é insignificante. A variação de velocidade da luz, ao passar do vácuo para o ar, é ínfima. Assim podemos fazer experimentos de modo mais fácil para entendermos os fenômenos que ocorrem com a luz ao transitar de um meio transparente para outro.
Meio isotrópico: é todo meio em que a luz se propaga em linha reta em todas as direções.
Sejam dois meios isotrópicos com índices de refração absoluto $\color{Maroon}{n_{1}}$ e $\color{Maroon}{n_{2}}$. Se a luz passar do meio 1 para o meio 2, podemos estabelecer o índice de refração do meio 2 em relação ao meio 1.
$$\color{Brown}{n_{2,1} = \frac{v_{1}}{v_{2}}}$$
Sendo $n_{1} = \frac{c}{v_{1}}$ e $n_{2} = \frac{c}{v_{2}}$
é possível estabelecer que $v_{1}\times n_{1} = c$ e $v_{2}\times n_{2} = c$
Isso nos permite dizer que $v_{1}\times n_{1} = v_{2}\times n_{2}$
Daí resulta que: $\color{Maroon}{\frac{v_{1}}{v_{2}} = \frac{n_{2}}{n_{1}}}$
Como vimos acima: $$\color{Navy}{n_{2,1} = \frac{v_{1}}{v_{2}} = \frac{n_{2}}{n_{1}}}$$
As velocidades da luz em dois meios isotrópicos são inversamente proporcionais aos seus índices de refração em relação ao vácuo (ar).
Obs.: O índice de refração absoluto de um meio transparente é sempre maior do que a unidade, pelo fato de ser o resultado da divisão da velocidade da luz no vácuo pela velocidade da luz no meio considerado.
Sendo $\color{Navy}{c > v}$$\Rightarrow$$\color{Navy}{n > 1}$.
Leis da refração ou Leis de Descartes-Snell
Foram Willebrord Snellius e Renné Descartes que estabeleceram as duas leis para a refração da luz. Vamos a elas.
Primeira lei da refração
O raio incidente, o raio refratado e a linha normal estão contidos no mesmo plano.
Segunda lei da refração
A velocidade de propagação da luz num meio $\color{Maroon}{1}$ é diretamente proporcional ao seno do ângulo de incidência, assim como a velocidade da luz no meio $\color{Maroon}{2}$ é diretamente proporcional ao seno do ângulo de refração.
$\frac{v_{1}}{sen(\hat{i})} = \frac{v_{2}}{sen(\hat{r})}$
$\frac{v_{1}}{v_{2}} = \frac{sen(\hat{i})}{sen(\hat{r})}$
Resumindo teremos:
$$\color{Navy}{n_{2,1} = \frac{v_{1}}{v_{2}} = \frac{n_{2}}{n_{1}} = \frac{sen(\hat{i})}{sen(\hat{r})}$$
Esta sequência de igualdades permite encontrar solução para a maioria das questões que envolvem a refração da luz em dioptros planos, paralelos ou curvos.
Desvio angular do raio refratado: é obtido calculando a diferença entre o ângulo de incidência e de refração.
$$\color{Blue}{\delta = {\hat{i} – \hat{r}}}$$
Se ${\delta > 0}$$\Rightarrow$ o desvio foi de aproximação da normal.
Se ${\delta < 0}$ $\Rightarrow$ o desvio foi de afastamento da normal.
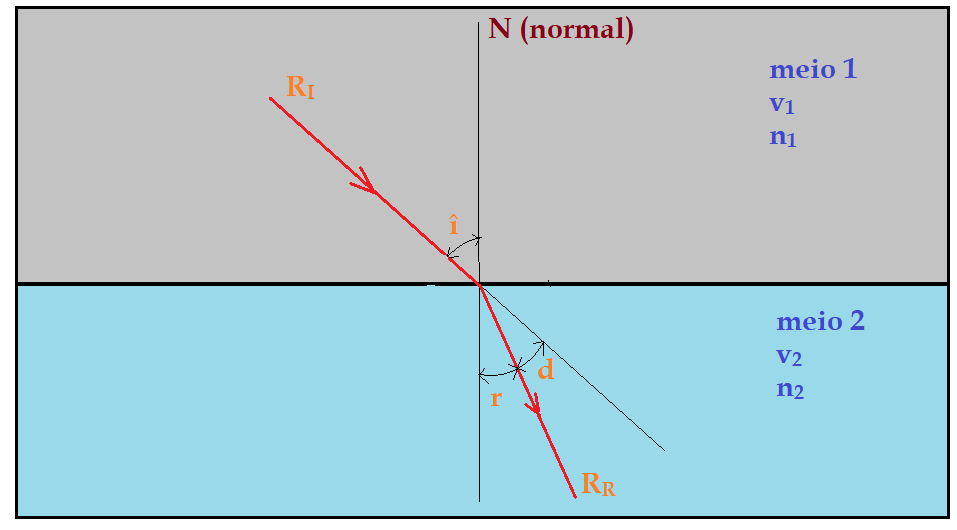
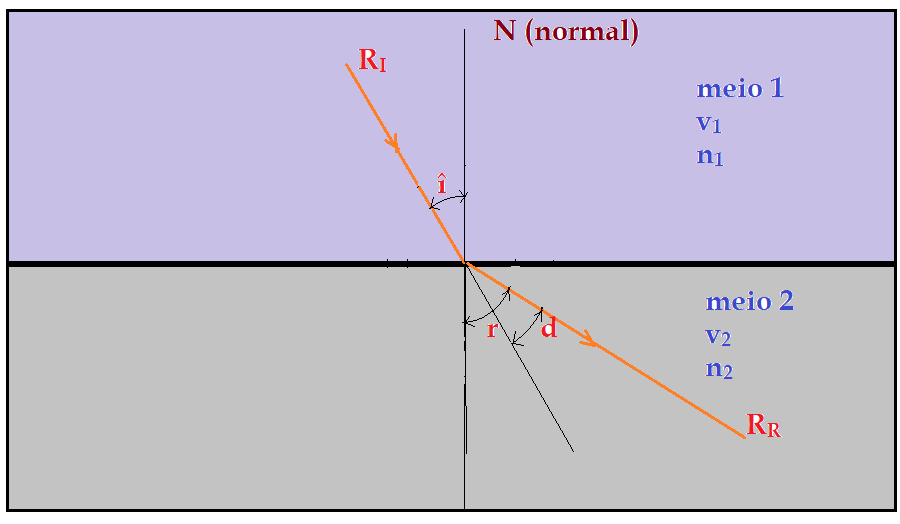
Ângulo limite
Quando $\color{Maroon}{n_{2}>n_{1}}$$\Rightarrow$ teremos um ângulo limite de refração que corresponde a um ângulo de incidência $\color{Maroon}{(\hat{i}) =90^{0}}$.
Quando $\color{Maroon}{n_{2}<n_{1}}$$\Rightarrow$ o ângulo limite será de incidência que corresponde a um ângulo de refração $\color{Maroon}{\hat{r} = 90^{0}}$ (rasante).
.
$\frac{v_{1}}{v_{2}} = \frac{n_{2}}{n_{1}} = \frac{sen (L_{i})}{sen (90^{0})}$
$\frac{n_{2}}{n_{1}} = \frac{sen(L_{i})}{sen(90^{0})}$
$\frac{n_{2}}{n_{1}} = \frac{sen(L_{i})}{1}$
$$\color{Navy}{sen(L_{i}) = \frac{n_{2}}{n_{1}}}$$
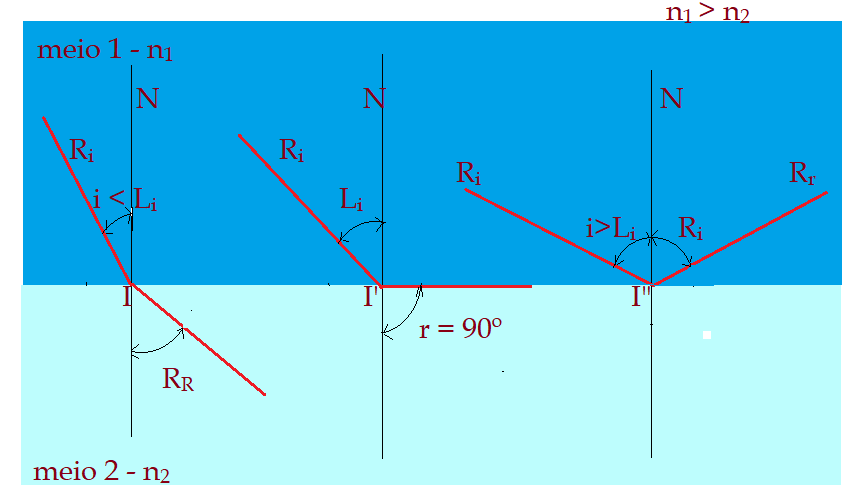
Reflexão total
Quando um raio luminoso incide num dioptro, indo do meio mais refringente para o menos refringente, ocorre como vimos o ângulo limite. Isso causa uma situação denominada Reflexão total. Ela acontece quando o ângulo de incidência é maior que o ângulo limite. Podemos analisar isso da seguinte forma:
${i > Li}$$\Rightarrow$ ocorre reflexão total do raio luminoso.
${i = Li}$$\Rightarrow$ o ângulo de refração é aproximadamente igual a $90^{0}$.
${i < Li}$$\Rightarrow$ ocorre a refração num ângulo maior que o de incidência.
Vamos exercitar antes de continuar!
- Um raio luminoso monocromático incide sobre um dioptro plano, formado pelos meios $\color{Maroon}{a}$ e $\color{Maroon}{b}$. O ângulo de incidência em relação à reta normal no ponto de incidência é $\color{Maroon}{i = 45^{0}}$ e se refrata por um ângulo $\color{Maroon}{r = 30^{0}}$ em relação à mesma normal. Determine o índice de refração do meio $\color{Maroon}{b}$ em relação ao meio $\color{Maroon}{a}$. Qual foi o desvio angular do raio luminoso?
$$\color{Maroon}{n_{b,a} = \frac{sen i}{sen r}}$$
$i = 45^{0}$ e $r = 30^{0}$
$n_{b,a} = \frac{sen (45^{0})}{sen(30^{0})}$
$n_{b,a}= \left[\frac{\left(\frac{\sqrt{2}}{2}\right)}{\left(\frac{1}{2}\right)}\right]$
$n_{b,a} = \left(\frac{\sqrt{2}}{2}\right)\times \left(\frac{2}{1}\right)$$\Leftrightarrow$$\color{Indigo}{n_{b,a} = \sqrt{2}}$
$\delta = {\hat{i} – \hat{r}}$$\Leftrightarrow$$\delta = {45^{0} – 30^{0}}$
$$\color{Navy}{\delta = 15^{0}}$$
O raio luminoso sofreu um desvio de $\color{Blue}{\delta = 15^{0}}$, aproximando-se da normal.
2. Um dioptro plano é formado pelos meios cujos índices de refração absolutos são $\color{Maroon}{n_{1}= \sqrt[3]{2}}$ e $\color{Maroon}{n_{2} = \sqrt[3]{3}}$. Se o raio luminoso incide do meio 1 para o meio dois, por um ânglo $\color{Maroon}{i = 30^{0}}$, determine o ângulo de refração. Se o sentido fosse o inverso, isto é, passando do meio 2 para o meio 1, no mesmo ângulo de incidência, qual seria o ângulo de refração?
$n_{1} = \sqrt[3]{2}$; $n_{2} = \sqrt[3]{3}$ e ${i = 30^{0}}$
$\frac{sen (i)}{sen (r)} = \frac{n_{2}}{n_{1}}$
$\frac{sen(30^{0})}{sen (r)} = \frac{\sqrt[3]{3}}{\sqrt[3]{2}}$
$\frac{\frac{1}{2}}{sen (r)} = \sqrt[3]{\frac{3}{2}}$
$sen(r) = \sqrt[3]{\frac{2}{3}}\times\frac{1}{2}$
$ r = arco seno \left(\frac{1}{2}\times\sqrt[3]{\frac{2}{3}}\right)$
Se o raio luminoso incidir do meio 2 para o meio 1 por um ângulo de 30º em relação à reta normal teremos:
$\frac{sen(30^{0})}{sen(r)} = \frac{n_{1}}{n_{2}}$
$\frac{\frac{1}{2}}{sen(r)} = \frac{\sqrt[3]{2}}{\sqrt[3]{3}}$
$sen (r) = \frac{1}{2}\times\frac{\sqrt[3]{3}}{\sqrt[3]{2}}$
$sen(r) = \frac{1}{2}\times\sqrt[3]{\frac{3}{2}}$
$r = arcsen\left(\frac{1}{2}\times\sqrt[3]{\frac{3}{2}}\right)$
3. Um raio de luz incide de um meio de $\color{Maroon}{n_{1} =\sqrt{5}}$ para um meio de $\color{Maroon}{n_{2} = \sqrt{3}}$. Qual é o ângulo limite de incidência $\color{Maroon}{L_{i}}$?
$sen(L_{i}) = \frac{n_{2}}{n_{1}}$
${{sen(L_{i})} = {{\sqrt{3}}\over{\sqrt{5}}}}$
$sen(L_{i}) = \sqrt{\frac{3}{5}}$
$$\color{Navy}{L_{i} = arcoseno (\sqrt{\frac{3}{5}})}$$
4)Um raio luminoso monocromático incide num dioptro plano, formado pelos meios transparentes e isótropos. O meio que contém o raio incidente$\color{Maroon}{R_{i}}$ tem índice de refração $\color{Maroon}{n_{1}=\sqrt{3}}$. O raio refratado forma com a normal um ângulo $\color{Maroon}{r = 60^{0}}$ e o índice de refração do meio é $\color{Maroon}{n_{2}=\sqrt{2}}$. Determine o ângulo de incidência desse raio luminoso.
$n_{1}=\sqrt{3}$; $n_{2}=\sqrt{2}$ e $r = 60^{0}$
$sen(i)\times n_{1} = sen (60^{0})\times n_{2}$
$sen(i)\times\sqrt{3} = \frac{\sqrt{3}}{2}\times\sqrt{2}$
$sen (i)=\frac{\sqrt{3}\times\sqrt{2}}{2\times\sqrt{3}}$
$sen (i)= \frac{\sqrt{2}}{2}$
$$\color{Navy}{i = 45^{0}}$$
Vamos trabalhar que é sua vez
- Um raio luminoso se propaga no ar $\color{Maroon}{n_{ar}=1}$ e atinge a superfície plana de uma lâmina de vidro. O índice de refração do vidro é $\color{Maroon}{n_{vidro}=1,4}$. Determine a medida do ângulo de refração, quando o ângulo de incidência $\color{Maroon}{i = 30^{0}}$.
- Determine o ângulo limite para um dioptro formado por dois meios transparentes e isótropos, sendo o menos refringente o ar $\color{Maroon}{n_{ar}=1}$ e o outro com índice de refração $\color{Maroon}{n_{2} = \sqrt{3}}$.
- Na refração de um raio luminoso monocromático, os ângulos de refração e de incidência valem, respectivamente, $\color{Maroon}{45^{0}}$ e $\color{Maroon}{30^{0}}$. Determine o índice de refração relativo do meio que contém o raio refratado em relação ao meio que contém o raio incidente.
- (Fatec-SP) – Na figura, um raio de luz monocromático se propaga pelo meio 1, de índice de refração $\color{Maroon}{2}$.
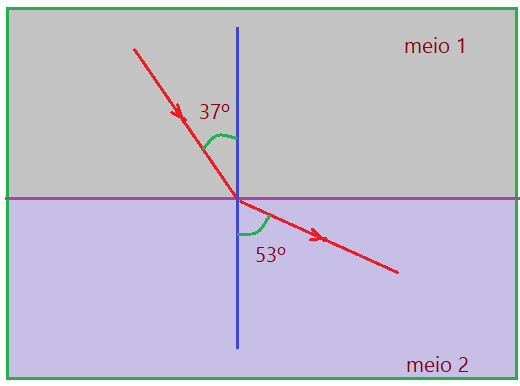
Com base nessas informações, determine o índice de refração do meio 2.
Dados: $sen(37^{0})= 0,60$ e $sen(53^{0}) = 0,80$
5. A luz vermelha se propaga no vácuo com velocidade $\color{Maroon}{c_{v}=3\times 10^{8}\,m/s}$ e no vidro com velocidade de $\color{Maroon}{v_{v}=2,5\times 10^{8}\,m/s}$. Um raio de luz que se propaga do vidro para o vácuo incide com $\color{Maroon}{\hat{i}=30^{0}}$ em relação à normal.
a. Determine o seno do ângulo de refração
b. Faça um esquema da refração.
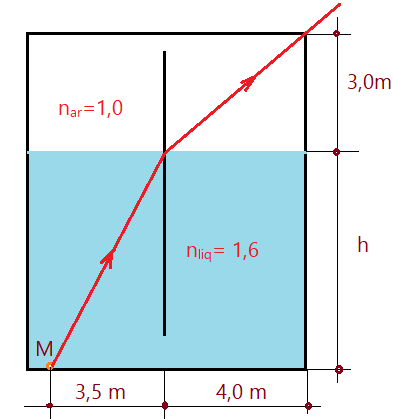
6. Um recipiente contém líquido de índice de refração absoluto igual à $\color{Maroon}{n_{liq}=1,6}$, até uma altura h. Um raio de luz proveniente de uma fonte de luz M, que está no fundo do recipiente, se refrata na superfície do líquido e passa rente à parede lateral do recipiente, como mostra o esquema abaixo. Considerando as medidas da figura, determine o valor da altura h.
07. Calcule o índice de refração do vidro, se a luz que atravessa a placa possui velocidade $\color{Maroon}{v_{v}= 2\times 10^{8}\,m/s}$. Considere o valor da velocidade da luz no vácuo: $\color{Maroon}{c = 3\times 10^{8}\,m/s}$.
08. (UERN) – Um feixe de luz proveniente de um meio A propaga-se em direção à superfície de separação com um meio B. Se o índice de refração do meio B em relação ao meio A é igual a $\color{Maroon}{n_{BA}=1,25}$, ao sofrer a refração, o feixe de luz teve sua velocidade:
( )a) reduzida em $25\%$;
( )b) reduzida em $20\%$;
( )c) aumentada em $20\%$;
( )d) aumentada em $25\%$;
( )e) mantida constante.
09. (PUC-Camp-SP) – Há uma série de fenômenos observáveis que ocorrem na atmosfera terrestre e que são determinados pela refração da luz ao percorrê-la. São exemplos o arco-íris, a formação de halos ao redor da Lua, a posição aparente dos astros mais elevada que a real, o fenômeno das miragens no deserto, a aurora boreal. A refração é o fenômeno da mudança na velocidade da propagação da luz ao passar de um meio transparente para outro. Considere um raio luminoso que forma ângulos iguais a $\color{Maroon}{45^{0}}$ e $\color{Maroon}{60^{0}}$ com a superfície que separa o vácuo do meio transparente e homogêneo M, como representado na figura.
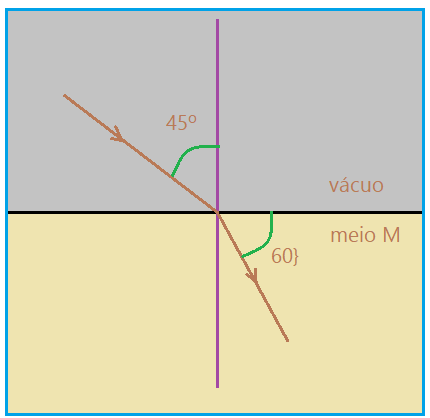
Dados:
Velocidade da luz no vácuo = 3,0 . 108 m/s
De acordo com a situação apresentada, a velocidade da luz no meio M, em m/s, vale:
( )a) $1,0\times 10^{8}$;
( )b) $1,0\sqrt{2}\times 10^{8}$;
( )c) $1,5\times 10^{8}$;
( )d) $1,0\times\sqrt{3}\times 10^{8}$;
( )e) $1,5\sqrt{2}\times 10^{8}$.
10. Um raio de luz monocromático incide na superfície de separação entre dois meios com índice de refração igual a $\color{Maroon}{n_{1} =1,5}$ e $\color{Maroon}{n_{2} = 2,0}$, passando do menor para o maior índice. Determine o ângulo de refração sabendo que o ângulo de incidência é de $\color{Maroon}{\hat{i}= 30^{0}}$.
( )a) $14^{0}$;
( )b) $18^{0}$;
( )c) $22^{0}$;
( )d) $26^{0}$;
( )e) $28^{0}$.
11. Ao sofrer refração de um meio com índice de refração $\color{Maroon}{n_{1}}$ para outro com índice de refração $\color{Maroon}{n_{2}}$, um raio de luz monocromático tem seu ângulo de incidência reduzido em $\color{Maroon}{\delta =5^{0}}$. Marque a alternativa que traz uma informação incorreta a respeito dessa refração.
( )a) Esse raio de luz passou de um meio de menor índice para outro de maior índice de refração;
( )b) A alteração no ângulo deve-se a uma diminuição da velocidade de propagação da luz;
( )c) O índice de refração relativo entre os meios 1 e 2 é menor que 1;
( )d) O índice de refração relativo entre os meios 2 e 1 é menor que 1;
( )e) Na passagem de n1 para n2, a velocidade da luz é reduzida.
10. (Fatec-SP) – Durante um ensaio com uma amostra de um material transparente e homogêneo, um aluno do Curso de Materiais da Fatec precisa determinar de que material a amostra é constituída. Para isso, ele utiliza o princípio da refração, fazendo incidir sobre uma amostra semicircular, de raio r, um feixe de laser monocromático, conforme a figura.
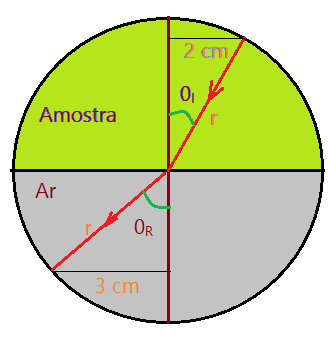
| Material | n |
| Ar | 1 |
| Policarbonato | 1,59 |
| Resina | 1,50 |
| Cristal dopado | 1,60 |
| Cristal de titânio | 1,71 |
| Cristal de lantânio | 1,80 |
Utilizando os dados da figura e as informações apresentadas na tabela de referência, podemos concluir corretamente que o material da amostra é
Lembre-se de que: $n_{I}\times sen\theta_{I} = n_{R}\times sen\theta_{R}$
( )a) cristal de lantânio;
( )b) cristal de titânio;
( )c) cristal dopado;
( )d) policarbonato;
( )e) resina.
13. (Uefs-BA) – Um raio luminoso incide sobre a superfície de separação entre o ar e o vidro com um ângulo $\color{Maroon}{\alpha = 60^{0}}$ e refrata com um ângulo $\color{Maroon}{\beta = 30^{0}}$, como mostra a figura.
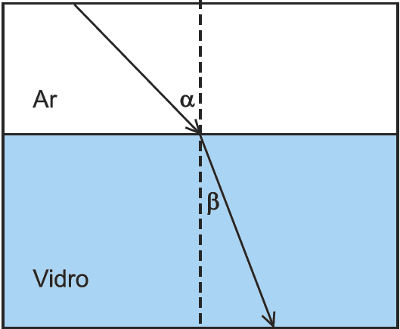
Considerando $\color{Brown}{sen(30)^{0} = cos(60)^{0} = 0,5}$; $\color{Brown}{sen(60)^{0} = cos(30)^{0} = 0,87}$; o índice de refração do ar igual a $\color{Brown}{n_{ar}=1}$ e o índice de refração do vidro igual a n, então o valor de n é igual a:
( )a) 1,48;
( )b) 1,57;
( )c) 1,63;
( )d) 1,74;
( )e) 1,82.
14. Um raio de luz incide sobre a superfície de separação entre os meios A e B com ângulo de incidência de $\color{Maroon}{\hat{i}=30^{0}}$. Sendo o ângulo de refração igual a $\color{Maroon}{\hat{r}=60^{0}}$, determine a razão de $\color{Maroon}{\frac{n_{A}}{n_{B}}}$.
Dados: $\color{Maroon}{sen(30)^{0} = 0,5}$; $\color{Maroon}{sen(60)^{0} = 0,87}$
( )a) 1,50;
( )b) 1,66;
( )c) 1,72;
( )d) 1,74;
( )e) 1,86.
15. Um raio de luz incide sobre a superfície de separação entre dois meios, formando um ângulo de $\color{Maroon}{\hat{i}=45^{0}}$ com a reta normal. Ao sofrer refração, o ângulo entre o raio de luz e a normal passa a ser de $\color{Maroon}{\hat{r}=30^{0}}$. Marque a alternativa correta a respeito do ocorrido:
( )a) Houve aumento de velocidade da luz, por isso o raio de luz de aproximou da reta normal;
( )b) Houve diminuição da velocidade da luz, logo pode-se concluir que o meio incidente possui maior índice de refração;
( )c) Como houve aproximação da reta normal, pode-se concluir que o índice de refração do meio para o qual a luz se deslocou é maior;
( )d) Se a lei de Snell for aplicada para esse caso, o resultado mostrará o mesmo valor para os índices de refração;
( )e) A luz aproxima-se da normal por causa de um aumento do índice de refração, porém sua velocidade de propagação foi mantida.
16. A refração da luz ocorre quando a luz atravessa algum meio refringente. Em relação a esse processo, podemos afirmar que:
( )a) no processo de refração, a frequência da luz não se altera;
( )b) no processo de refração, a velocidade da luz permanece constante;
( )c) ao sofrer refração, a velocidade da luz e o seu comprimento de onda diminuem;
( )d) na refração, a velocidade da luz só pode diminuir;
( )e) na refração, a velocidade da luz só pode aumentar.
17. O fenômeno responsável pela ilusão de óptica que dá origem às miragens é conhecido como
( )a) reflexão;
( )b) refração;
( )c) difração;
( )d) dispersão;
( )e) espalhamento.
18. O índice de refração de um meio óptico transparente é de $\color{Maroon{n = 1,8}$. Em relação isso, é possível afirmar que
( )a) a velocidade da luz nesse meio é 1,8 vezes mais rápida do que no vácuo;
( )b) a velocidade da luz nesse meio é 1,8 vezes mais lenta do que no vácuo;
( )c) a frequência da luz refratada nesse meio é 1,8 vezes menor do que no vácuo;
( )d) o comprimento de onda não sofre nenhuma alteração;
( )e) o comprimento de onda aumenta.
19. (UN. MACKENZIE) – A velocidade de propagação da luz em determinado líquido é 80% daquela verificada no vácuo. O índice de refração desse líquido é:
( )a)1,50;
( )b)1,25;
( )c)1,00;
( )d) 0,80;
( )e) 0,20.
20. A luz atravessa um material feito de plástico com velocidade $\color{Maroon}{v = 1,5\times 10^{8}\,m/s}$. Sabendo que a velocidade da luz no vácuo é $\color{Maroon}{c=3,0\times 10^{8}\,m/s}$, calcule o índice de refração do plástico.
21. Um raio de luz atravessa a interface entre o ar e um líquido desconhecido, mudando sua direção conforme mostra a figura abaixo. Sabendo que o índice de refração do ar é $\color{Maroon}{n_{ar}=1}$, calcule o índice de refração do líquido. Dados: $\color{Maroon}{sen(35)^{0} = 0,57}$ e $\color{Maroon}{sen(20)^{0} = 0,34}$

22. (PUC-RIO 2007) – Um feixe de luz de comprimento de onda de $\color{Maroon}{\lambda = 600\,nm}$ se propaga no vácuo até atingir a superfície de uma placa de vidro. Sabendo-se que o índice de refração do vidro é $\color{Maroon}{n_{v} = 1,5}$ e que a velocidade de propagação da luz no vácuo é de $\color{Maroon}{c = 3\times 10^{8}\,m/s}$, o comprimento de onda e a velocidade de propagação da onda no vidro em $\color{Maroon}{nm; m/s}$, respectivamente, são: (Obs: $1 nm = 1 x 10^{-9}\,m$).
( )a) $200\,nm; 4 \times 10^{8}\,m/s$;
( )b) $200\,nm; 3\times 10^{8}\,m/s$;
( )c) $200\,nm; 2\times 10^{8}\,m/s$;
( )d) $400\,nm; 1\times 10^{8}\,m/s$;
( )e) $400\,nm; 2\times 10^{8}\,m/s$.
Se ficarem dúvidas, use um dos canais para comunicar-se comigo e esclareceremos as dificuldades. Mesmo se você tiver outros exercícios, de outra origem, também ajudo a resolver.
Curitiba, 30 de setembro de 2019. Atualizado em 14 de outubro de 2019.
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
