Física – Ótica Geométrica – Espelhos esféricos
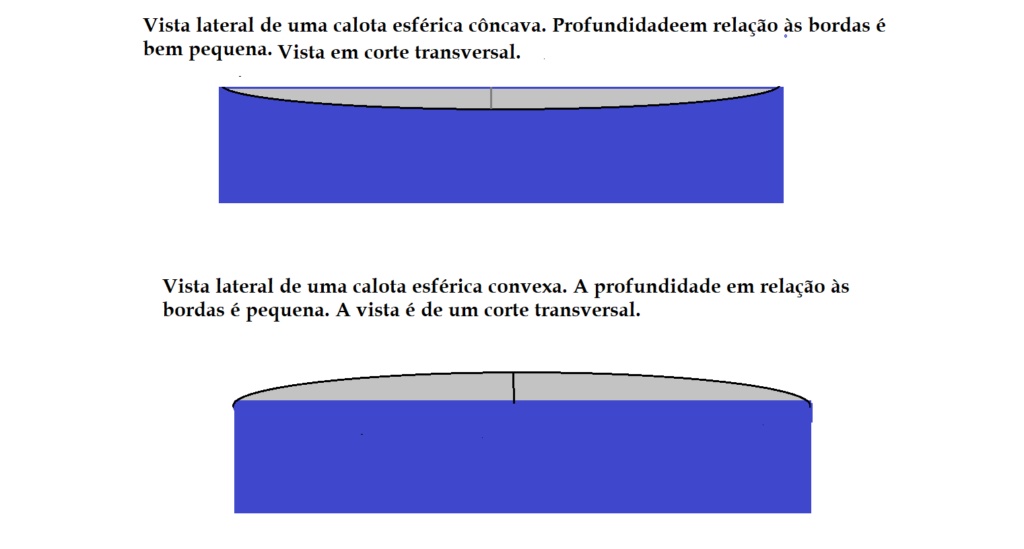
Os espelhos esféricos são formados de calotas esféricas. Imagine cortar uma fatia de uma bola, que não precisa ser igual a metade, aliás, muito menos da metade. Isso nos dará o formato de um espelho esférico. Dependendo do lado que for espelhado, teremos um espelho côncavo ou um espelho convexo.
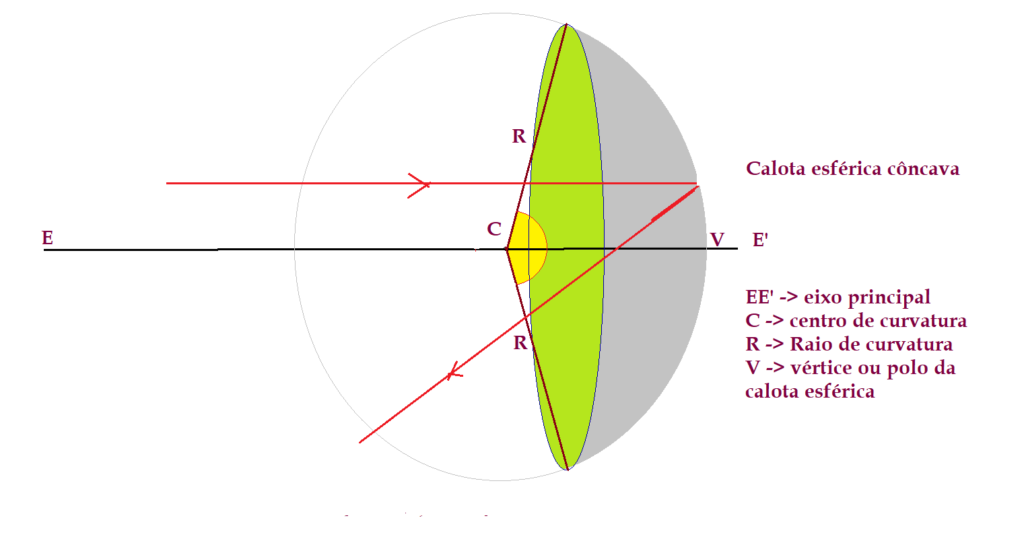
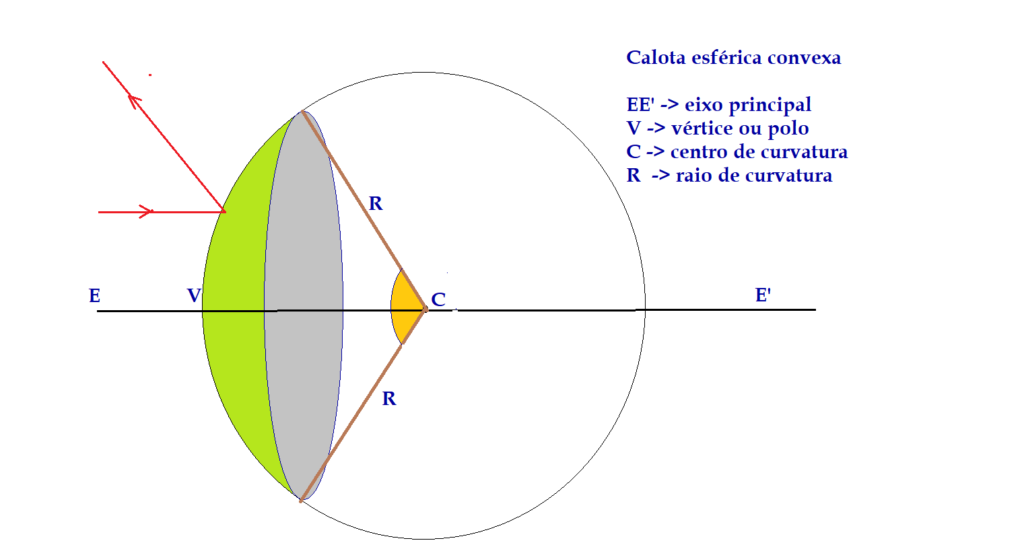
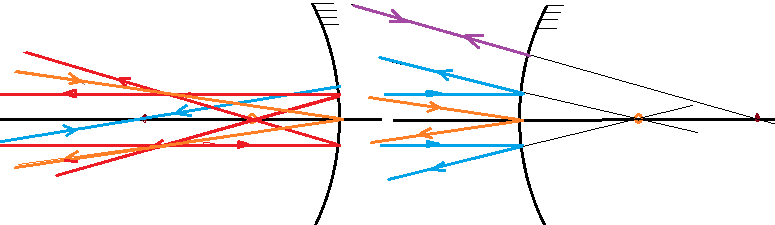
Tanto os espelhos côncavos como os convexos, se usarmos as suas bordas para obter imagens, estas, sofrem distorções, denominadas aberrações esféricas, que são tanto de forma como de cor.
Pontos importantes dos espelhos esféricos
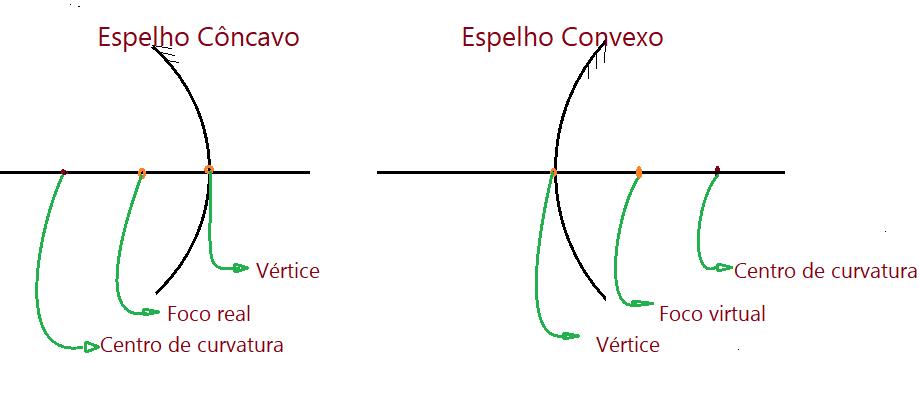
Antes de mais nada vejamos algumas características próprias dos espelhos esféricos, quanto aos raios de luz que incidem e são refletidos. Observando as figuras mostradas acima, pode-se ver que o Centro de Curvatura e o Foco dos espelhos côncavos ficam situados antes do espelho. Isso dá ao foco a denominação de foco real. Já no espelho convexo, o centro e o foco ficam atrás do espelho, de modo que o foco recebe a denominação de foco virtual. Essa distinção é devida ao fato de que no côncavo, quem passa pelo foco, são os próprios raios de luz, refletidos ou incidentes. No convexo os raios são refletidos e o foco é determinado pelos prolongamentos dos raios refletidos.
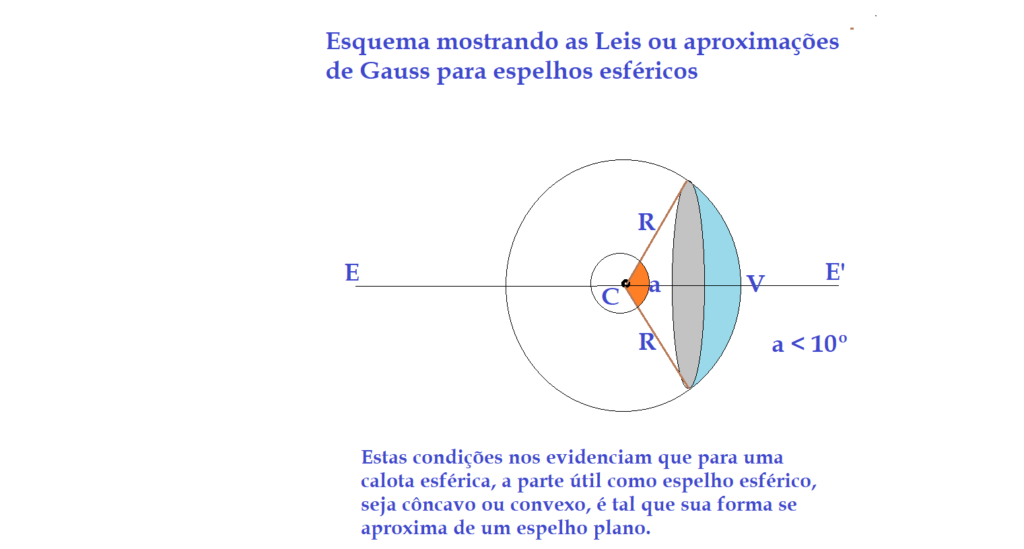
NOTA.: Os espelhos côncavos e convexos, são representados para efeitos de estudos da formação de imagens e estabelecimento das equações, são representados por um arco de círculo, como mostram as figuras a seguir.
Um físico importante, de nome Gauss, estudando os espelhos esféricos, observou alguns fatos notáveis. Esses fatos são:
- O raio luminoso que incide sobre o espelho esférico paralelamente ao eixo principal, sofre reflexão numa direção que passa pelo foco.
- O raio luminoso que incide sobre o espelho esférico passando pelo foco, reflete-se paralelamente ao eixo principal.
- O raio luminoso que incide no vértice do espelho, sofre reflexão de modo simétrico em relação ao eixo do espelho.
- O raio luminoso que incide no espelho plano, numa direção que passa pelo centro de curvatura, sofre reflexão sobre si mesmo (o ângulo de incidência é normal, isto é igual a 0º com a reta normal, o que é o mesmo que ser perpendicular à tangente da curva no ponto considerado.
- Um raio luminoso que passe pelo centro de curvatura ${C}$, vértice ${V}$, é coincidente com o que denominamos eixo principal. Qualquer reta que passe pelo centro e intercepte a calota do espelho em um ponto qualquer é um eixo secundário e determinará um foco secundário.
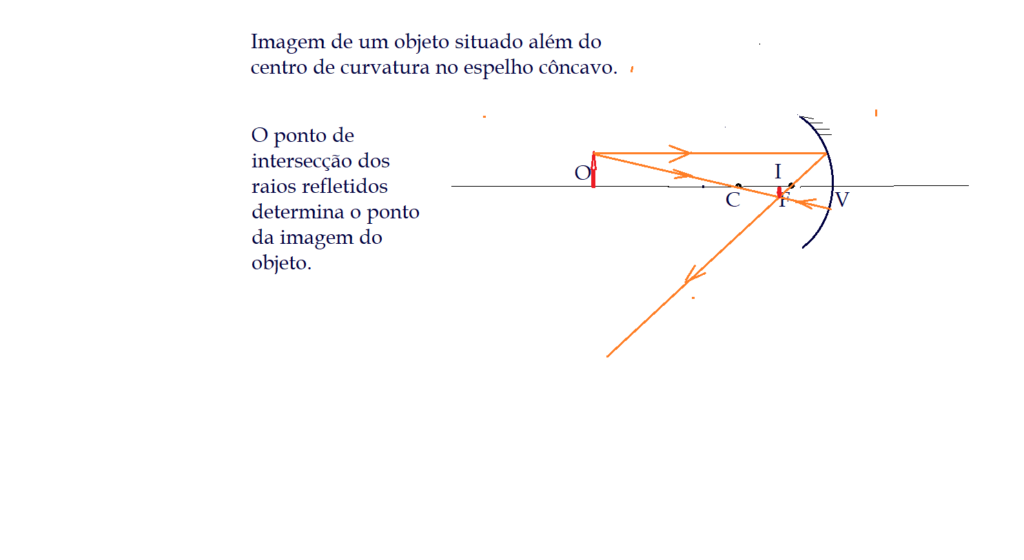
Formação de imagens nos espelhos côncavos
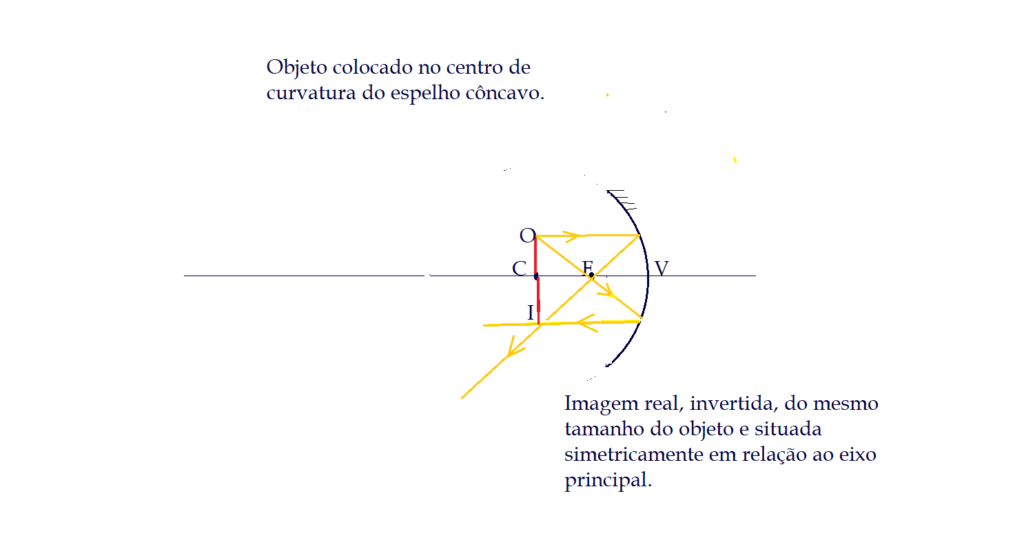
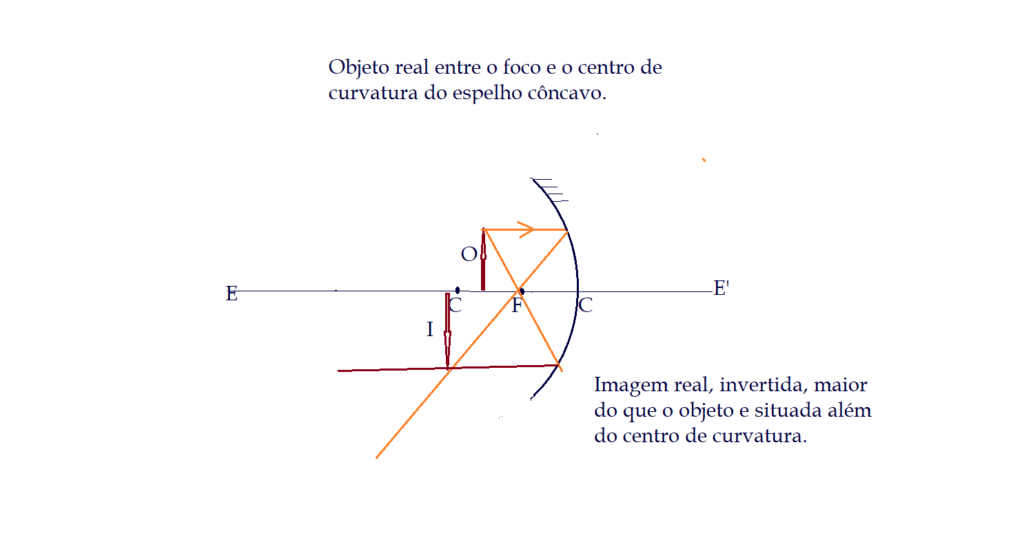
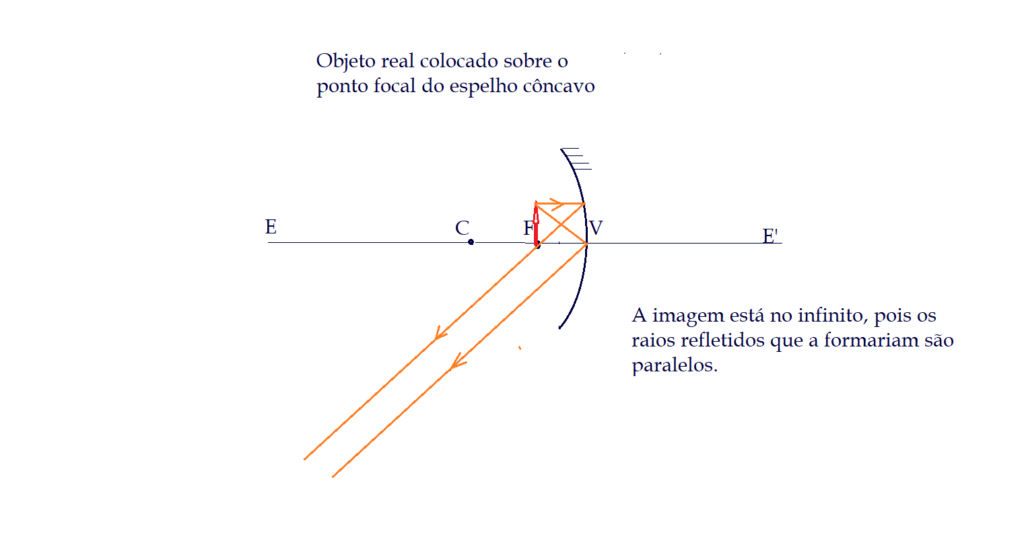
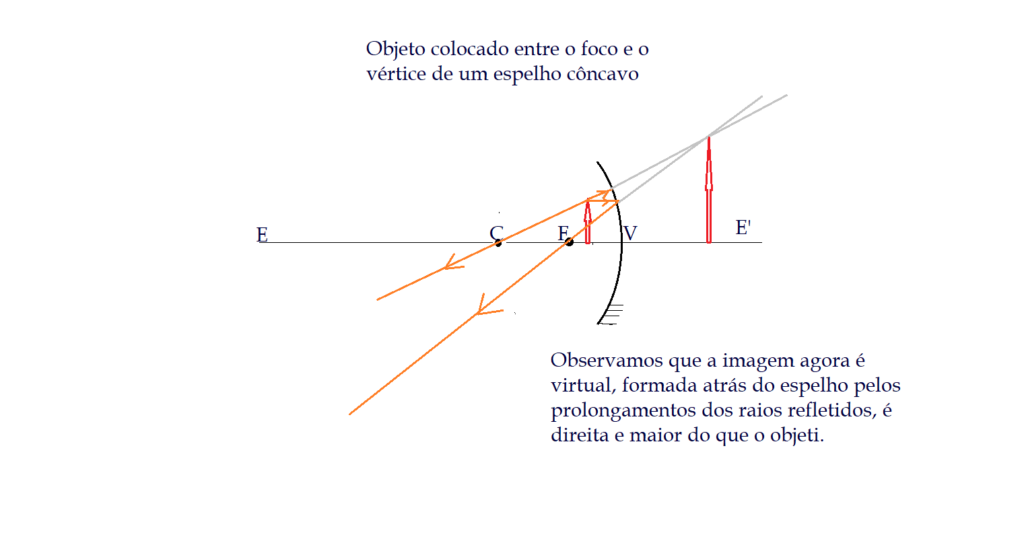
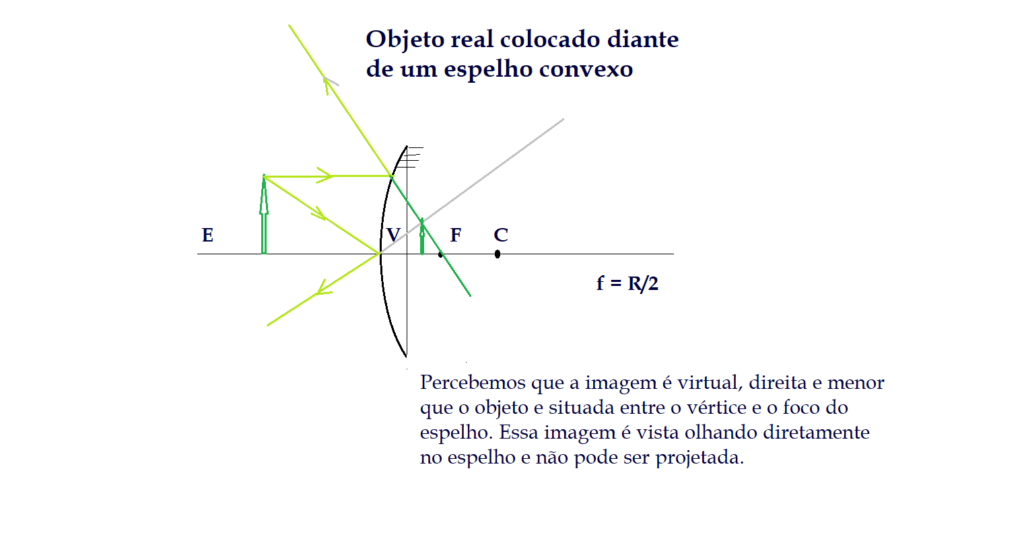
Formação de imagens nos espelhos convexos.
A formação de imagens nos espelhos convexos é menos variada do que nos espelhos côncavos. Note que o foco e o centro de curvatura estão colocados atrás do espelho e os objetos reais não podem ser colocados atrás do espelho queremos que haja formação de imagem.
Leis de nitidez de Gauss
Depois que estabelecemos as figuras com a formação de imagens de objetos em espelhos esféricos, chegou o momento de estudar as chamadas Leis ou Aproximações de Gauss que nos permitem obter imagens com razoável nitidez, permitindo a aplicação dos espelhos em aplicações práticas.
1ªLei de Gauss: Para que o espelho esférico possa fornecer imagens nítidas, seu ângulo de abertura deve ser pequeno ($\color{Maroon}{\alpha \leq {10^{0}}}$).
2ª Lei de Gauss: Os raios incidentes no espelho devem ser ser paralelos ou muito pouco inclinados em relação ao eixo principal do espelho.
3ª Lei de Gauss: Os raios incidentes devem estar próximos ao eixo principal do espelho.
Traduzindo isso em desenhos teremos:
Equação de Gauss para os espelhos esféricos
Vejamos um desenho construtivo de uma imagem e teremos a formação de triângulos semelhantes, de onde podemos deduzir a equação.
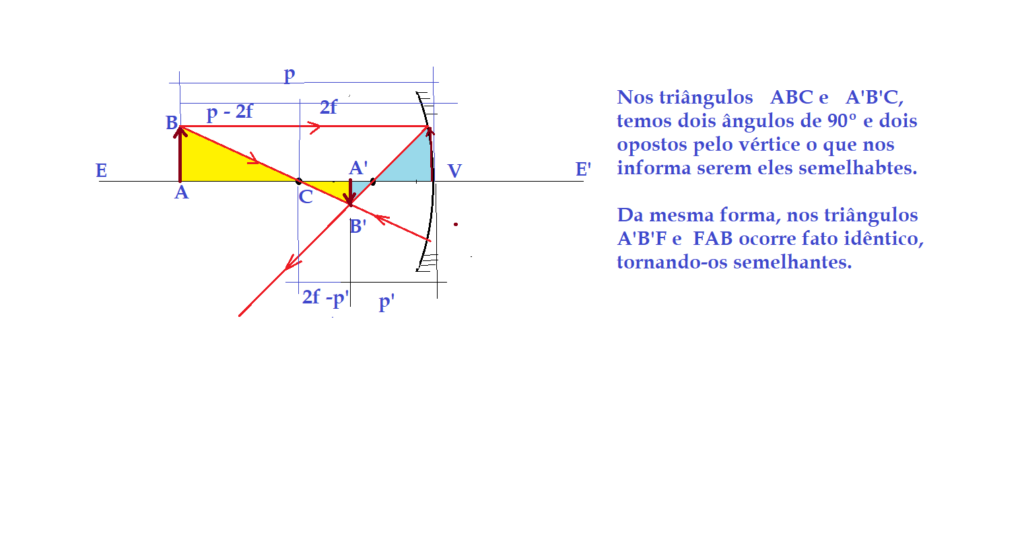
Nos dois primeiros triângulos podemos escrever:
$\frac{AB}{A’B’} = \frac{p – 2f}{2f-p’}$
$\frac{AB}{A’B’} = \frac{f}{f -(2f – p’)}$
Igualando as duas expressões ficamos com:
$\frac{p – 2f}{2f -p’} = \frac{f}{f – 2f + p’}$
Multiplicando os meios e os extremos da proporção, teremos:
${(p – 2f)}\cdot{(p’ – f)} = f\cdot{(2f – p’)}$
$p\cdot{p’} – p\cdot{f} – 2p’\cdot{f} + 2f^{2} = 2f^{2} – p’\cdot{f}$
Cancelando os termos simétricos e reduzindo os termos semelhantes.
$p\cdot{p’} – p\cdot{f} – p’\cdot{f} = 0$
Dividindo todos os termos por $pp’f$
$\frac{{p}\cdot{p’} – {p}\cdot{f} – {p’}\cdot{f}}{pp’f} = 0$
$\frac {1}{f} – \frac{1}{p’} – \frac{1}{p} = 0$
$$\color{Navy}{\frac{1}{f} = \frac{1}{p} + \frac{1}{p’}}$$
Temos aí a Equação de Gauss para os espelhos esféricos. Ela é aplicável tanto aos espelhos côncavos quanto aos convexos. Para isso bastará considerar as distâncias ${p}$, ${p’}$, ${f}$ e ${R}$ com os sinais apropriados. Quando se situam antes do espelho são positivas e depois do espelho negativas. Assim teremos:
${R\gt {0}}$$\Leftrightarrow$ espelho côncavo.
${R\lt {0}}$$\Leftrightarrow$ espelho convexo.
${f\gt {0}}$$\Leftrightarrow$ espelho côncavo.
${f\lt {0}}$$\Leftrightarrow$ espelho convexo.
${p\gt {0}}$$\Leftrightarrow$ objeto real.
${p’\gt{0}}$$\Leftrightarrow$ imagem real.
${p\lt {0}}$$\Leftrightarrow$ objeto virtual.
${p’\lt {0}}$$\Leftrightarrow$ imagem virtual.
Importante
Notamos que a imagem cresce na medida em que a posição do objeto fica mais próxima do espelho. O fato de ser invertida (de cabeça para baixo) torna sua “ampliação linear” negativa.
$$\color{Navy}{A = \frac{I}{O}}$$
Isso também acontece com as distâncias em relação ao vértice.
$$\color{Navy}{A = \frac{-p’}{p}}$$
Igualando temos então
$$\color{Red}{A = \frac{I}{O} = \frac{-p’}{p}}$$
Vamos fazer exercícios.
- Um espelho esférico côncavo, tem raio de curvatura igual a $\color{Maroon}{R = 60,0\,cm}$. Coloca-se um objeto retilíneo perpendicularmente ao eixo principal, a uma distância de $\color{Maroon}{90,0\,cm}$. Determine a posição da imagem. Estabeleça as características da imagem quanto à natureza, posição, e tamanho.
Temos que: $\color{Maroon}{R = 60,0\,cm}$
$ p = 90,0\,cm$
Se $f =\frac{R}{2}$$\Leftrightarrow$$f =\frac{60,0}{2} = 30,0\,cm$
Se $\frac{1}{f} = \frac{1}{p} + \frac{1}{p’}$$\Leftrightarrow$$\frac{1}{30,0} = \frac{1}{90,0} + \frac{1}{p’}$
$\frac{1}{p’} = \frac{1}{30,0} – \frac{1}{90,0}$
$\frac{1}{p’} = \frac{{1}\cdot{3}}{90} – \frac{1}{90,0}$
$\frac{1}{p’} = \frac{2}{90}$$\Leftrightarrow$$p’ = \frac{90,0}{2}$
$$\color{Brown}{p’ = 45,0\,cm}$$
Observamos que a distância da imagem ao vértice do espelho é também positiva e portanto a imagem é real, será invertida e menor que o objeto, conforme vimos nas ilustrações da formação de imagens.
A ampliação linear da imagem em relação ao objeto será dada por:
$$\color{Maroon}{A = \frac{I}{O} = \frac{- p’}{p}}$$
$A = \frac{- 45,0}{90,0}$$\Leftrightarrow$$\color{Maroon}{A = – \frac{1}{2}}$
2. Um espelho esférico tem raio de curvatura $\color{Maroon}{R = -40,0\,cm}$. Um objeto de $\color{Maroon}{h = 16,0\,cm}$ de altura é colocado perpendicularmente ao eixo principal. A imagem é formada na posição $\color{Maroon}{p’ = – 18,0\,cm}$ atrás do espelho. Pede-se determinar: a) a distância focal do espelho e sua natureza; b) a distância do objeto ao vértice; c) a ampliação linear da imagem em relação ao objeto e o seu tamanho; d) a posição da imagem (direita ou invertida).
a) Se $R = -40,0\,cm$$\Leftrightarrow$$f = \frac{-40,0}{2}$
$f = – 20,0\,cm$$\Rightarrow$ espelho convexo, foco virtual.
b)$\frac{1}{f} = \frac{1}{p} + \frac{1}{p’}$
$\frac{1}{- {20,0}} = \frac{1}{p} + \frac{1}{-18,0}$
$\frac{1}{p}= \frac{{1}\cdot{(- 9,0)} + {1}\cdot {10,0}}{180,0}$
$\frac{1}{p} = \frac{ – 9,0 + 10,0}{180,0}$$\Leftrightarrow$$p = 180,0\,cm$
c) $\color{Maroon}{A = \frac{I}{O} = \frac{-p’}{p}}$
$A = \frac{-{-18,0}}{180,0}$$\Leftrightarrow$$\color{Blue}{A = \frac{1}{10}}$
A imagem terá um décimo da altura do objeto.
$A = \frac{I}{O}$$\Leftrightarrow$$\frac{1}{10} = \frac{I}{16,0}$
$\frac{I}{16,0} = \frac{1}{10}$$\Leftrightarrow$$I = \frac{16,0}{10}$$\Leftrightarrow$$\color{Navy}{I = 1,6\,cm}$
d) a imagem é direita e tem um décimo da altura do objeto.
Exercícios para resolver
- Um objeto retilíneo de $\color{Maroon}{h = 30,0\,cm}$ é posicionado de maneira perpendicular ao eixo principal de um espelho esférico cujo raio é $\color{Maroon}{R = 50,0\,cm}$. A imagem formada é direita e mede $\color{Marooon}{45,0\,cm}$ de altura. Pergunto: a) qual é a posição dessa imagem em relação ao espelho? b) qual é a ampliação da imagem?c)qual é a posição do objeto em relação ao espelho? d) o espelho é côncavo ou convexo?
- Um espelho esférico convexo, forma a imagem de um objeto que mede $\color{Maroon}{O = 25,0\,cm}$, num ponto situado à $\color{Maroon}{p’ =- 30,0\,cm}$ atrás do vértice. Se a ampliação da imagem em relação ao objeto é $\color{Maroon}{A = \frac{1}{5}}$, determine: a)a posição do objeto em relação ao vértice do espelho; b) a distância focal do espelho; c) o raio de curvatura do espelho; d) este espelho pode fornecer imagem real para algum objeto real?
- Um objeto retilíneo de $\color{Maroon}{I =12,0\,cm}$ de altura, colocado perpendicularmente ao eixo principal de um espelho esférico côncavo, têm sua imagem com altura de $\color{Maroon}{I’=36,0\,cm}$ projetada sobre um anteparo, situado a uma distância de $\color{Maroon}{p’ = 120,0\,cm}$ do vértice do espelho. Determine: a) a distância do objeto ao espelho; b) a distância focal do espelho; c) o raio de curvatura do espelho; d) qual é a natureza da imagem?
04. Certo espelho esférico côncavo apresenta raio de curvatura igual a $\color{Maroon}{R = 0,5\,m}$. A distância focal desse espelho, em centímetros, é igual a:
( )a) 50 cm;
( )b) 10 cm;
( )c) 25 cm;
( )d) 150 cm;
( )e) 100 cm.
05. Um espelho esférico conjuga uma imagem virtual, direta e reduzida de um objeto real. Em relação a esse espelho e à posição do objeto da imagem, assinale a alternativa correta:
( )a) Trata-se de um espelho côncavo, quando o objeto é posicionado entre seu foco e vértice;
( )b) Trata-se de um espelho côncavo, quando o objeto é posicionado no foco do espelho;
( )c) Trata-se de um espelho côncavo, quando o objeto é colocado no centro de curvatura do espelho;
( )d) Trata-se de um espelho convexo, quando o objeto é colocado a qualquer distância de seu vértice;
( )e) Trata-se de um espelho convexo que conjuga imagens reais.
06. Um espelho esférico conjuga uma imagem virtual, direta e reduzida de um objeto real. Em relação a esse espelho e à posição do objeto da imagem, assinale a alternativa correta:
( )a) Trata-se de um espelho côncavo, quando o objeto é posicionado entre seu foco e vértice;
( )b) Trata-se de um espelho côncavo, quando o objeto é posicionado no foco do espelho;
( )c) Trata-se de um espelho côncavo, quando o objeto é colocado no centro de curvatura do espelho;
( )d) Trata-se de um espelho convexo, quando o objeto é colocado a qualquer distância de seu vértice;
( )e) Trata-se de um espelho convexo que conjuga imagens reais.
07. Um espelho esférico côncavo conjuga uma imagem real de um objeto que é colocado a $\color{Maroon}{p = 20\,cm}$ de seu vértice. Sabendo que a distância focal desse espelho é de $\color{Maroon}{f = 10\,cm}$, determine a distância dessa imagem formada até o objeto.
( )a) 10 cm;
( )b) 30 cm;
( )c) 40 cm;
( )d) 20 cm;
( )e) 0 cm.
08. (UFPB 2008) – Com relação a uma experiência envolvendo espelhos curvos, em um determinado laboratório, considere as afirmativas abaixo:
I. A imagem de um objeto, colocado na frente de um espelho convexo, é sempre virtual.
II. A imagem de um objeto, colocado na frente de um espelho côncavo, é sempre real.
III. A distância focal é sempre igual ao raio do espelho.
IV. A imagem de um objeto, projetada em um anteparo, é sempre real.
Estão corretas apenas:
( )a) III e IV;
( )b) II e IV;
( )c) I e IV;
( )d) II e III;
( )e) I e II.
09. (UDESC 2017/1) – Um lápis foi colocado a $\color{Maroon}{p = 30,0\,cm}$ diante de um espelho esférico convexo de distância focal igual a $\color{Maroon}{f = 50\,cm}$, perpendicularmente ao eixo principal. O lápis possui $\color{Maroon}{O = 10,0\,cm}$ de comprimento. Com base nestas informações, pode-se afirmar que a posição e o tamanho da imagem do lápis são, respectivamente:
( )a) 75,0 cm e -25,0 cm;
( )b) 18,75 mm e -6,25 mm;
( )c) -75,0 cm e 25,0 cm;
( )d) 75,0 cm e 6,25 cm;
( )e) -18,75 cm e 6,25 cm.
10. (PUC-SP 2018/1) – Considere dois espelhos esféricos, um côncavo e outro convexo, que obedeçam às condições de nitidez de Gauss. Esses espelhos possuem, em módulo, a mesma distância focal. De um objeto situado a uma distância $\color{Maroon}{P_{1}}$ da superfície refletora do espelho convexo, é conjugada uma imagem cujo aumento linear transversal é igual a $\frac{3}{4}$
Determine o módulo da relação $\color{Maroon}{\frac{P_{2}}{P_{1}}}$ para que, quando esse mesmo objeto estiver distante $\color{Maroon}{P_{2}}$ da superfície refletora do espelho côncavo, seja obtido o mesmo aumento linear em módulo.
( )a) 1;
( )b) 3;
( )c) 4;
( )d) 7;
( )e) 5.
11. (Unespar 2016) – Considere um espelho esférico côncavo e um objeto colocado entre o foco F e o centro de curvatura C.
Considere as características de imagens nas afirmativas a seguir:
I. Imagem real e menor que o objeto.
II. Imagem virtual e maior que o objeto.
III. Imagem real e maior que o objeto.
IV. Imagem de cabeça para baixo.
V. Imagem sem estar de cabeça para baixo.
Assinale a alternativa correta com relação à imagem que será formada:
( )a) As afirmativas I e IV estão corretas;
( )b) As afirmativas II e V estão corretas;
( )c) As afirmativas III e IV estão corretas;
( )d) As afirmativas II e IV estão corretas;
( )e) As afirmativas II e IV estão corretas.
12. (Unespar 2016) – Considere um objeto de $\color{Maroon}{O = 12\,cm}$ colocado a $\color{Maroon}{p = 10\,cm}$ de um espelho esférico convexo. Sabendo que a imagem é virtual e possui $\color{Maroon}{I = 6\,cm}$ de altura, a distância da imagem até o vértice do espelho e o raio de curvatura deste espelho são, respectivamente:
( )a) $D_{i} = -20,0\,cm$; $R = 120,0\,cm$;
( )b) $D_{i}= – 2\,cm$; $R = 20\,cm$;
( )c) $D_{i} = – 10\,cm$; $R = 10 cm$;
( )d) $D_{i} = – 20\,cm$; $R = 20\,cm$;
( )e) $D_{i} = -5,0\,cm$; $R = -20,0\,cm$.
13. (Unespar 2015) – Considere o espelho esférico côncavo de raio de curvatura $\color{Maroon}{R = 20\,cm}$. Considere ainda um objeto de $\color{Maroon}{O = 5\,cm}$ localizado a $\color{Maroon}{p =15\,cm}$ do vértice. Com relação às características da imagem formada, julgue os itens a seguir:
(2) A imagem será formada a 30 cm do vértice do espelho.
(4) A imagem terá 2,5 cm.
(8) A imagem será virtual e direita.
(16) A imagem será real e invertida.
(32) A imagem será duas vezes maior que o objeto.
(64) A imagem será formada sobre o centro de curvatura.
Assinale a alternativa que apresenta o somatório das afirmativas corretas.
( )a) 30;
( )b) 80;
( )c) 50;
( )d) 38;
( )e) 48.
14. Um objeto é posicionado $\color{Maroon}{p = 50\,cm}$ à frente de um espelho côncavo, cuja distância focal é de $\color{Maroon}{f = 25\,cm}$. Determine em qual posição forma-se a imagem desse objeto.
( )a) – 50 cm;
( )b) +50 cm;
( )c) + 25 cm;
( )d) – 40 cm;
( )e) + 75 cm.
15. Um objeto de $\color{Maroon}{O = 10\,cm}$ de altura é colocado a $\color{Maroon}{p = 30\,cm}$ de um espelho convexo, cuja distância focal é $\color{Maroon}{f= -10\,cm}$. Determine o tamanho da imagem conjugada por esse espelho.
( )a) – 5 cm;
( )b) – 10 cm;
( )c) – 25 cm;
( )d) – 50 cm;
( )e) – 100 cm.
16. É comum que se utilize espelhos côncavos em óticas, para que seja possível examinar detalhes das armações, graças à formação de imagens maiores que seus objetos. Para que um espelho côncavo possa formar imagens diretas e maiores do que seus objetos, é necessário posicionar o objeto:
( )a) entre o foco e o centro de curvatura;
( )b) entre o vértice e o foco;
( )c) além do centro de curvatura;
( )d) além do foco;
( )e) sobre o foco.
17. Certo espelho esférico côncavo apresenta raio de curvatura igual a $\color{Maroon}{R = 0,5\,m}$. A distância focal desse espelho, em centímetros, é igual a:
( )a) 50 cm;
( )b) 10 cm;
( )c) 25 cm;
( )d) 150 cm;
( )e) 100 cm.
18. Um espelho esférico conjuga uma imagem virtual, direta e reduzida de um objeto real. Em relação a esse espelho e à posição do objeto da imagem, assinale a alternativa correta:
( )a) Trata-se de um espelho côncavo, quando o objeto é posicionado entre seu foco e vértice;
( )b) Trata-se de um espelho côncavo, quando o objeto é posicionado no foco do espelho;
( )c) Trata-se de um espelho côncavo, quando o objeto é colocado no centro de curvatura do espelho;
( )d) Trata-se de um espelho convexo, quando o objeto é colocado a qualquer distância de seu vértice;
( )e) Trata-se de um espelho convexo que conjuga imagens reais.
19. Julgue as afirmações feitas acerca da formação de imagens por espelhos esféricos côncavos e convexos:
I – Espelhos côncavos podem conjugar imagens reais e virtuais.
II – Todo espelho convexo conjuga imagens virtuais.
III – Quando um objeto é colocado diante de um espelho côncavo, a uma distância maior que o seu centro de curvatura, a imagem formada é real, invertida e reduzida.
IV – Quando algum objeto é posicionado à frente de um espelho côncavo, exatamente em seu foco, os raios de luz refletidos pelo espelho não se cruzam.
São verdadeiras:
( )a) I e II;
( )b) I, II e III;
( )c) II e III;
( )d) I, II e IV;
( )e) Todas as alternativas.
20. Um espelho esférico côncavo conjuga uma imagem real de um objeto que é colocado a 20 cm de seu vértice. Sabendo que a distância focal desse espelho é de 10 cm, determine a distância dessa imagem formada até o objeto.
( )a) 10 cm;
( )b) 30 cm;
( )c) 40 cm;
( )d) 20 cm;
( )e) 0 cm.
21. (CESGRANRIO) – Um objeto de altura O é colocado perpendicularmente ao eixo principal de um espelho esférico côncavo. Estando o objeto no infinito, a imagem desse objeto será:
( )a) real, localizada no foco;
( )b) real e de mesmo tamanho do objeto;
( )c) real, maior do que o tamanho do objeto;
( )d) virtual e de mesmo tamanho do objeto;
( )e) virtual, menor do que o tamanho do objeto.
22. (UNIP) – Um estudante de Física deseja acender seu cigarro usando um espelho esférico e a energia solar. A respeito do tipo de espelho esférico e do posicionamento da ponta do cigarro, assinale a opção correta:
Espelho Posição da ponta do cigarro
( )a) côncavo centro de curvatura do espelho
( )b) côncavo vértice do espelho
( )c) côncavo foco do espelho
( )d) convexo centro de curvatura do espelho
( )e) convexo foco do espelho
23. (PUC) – Em um farol de automóvel tem-se um refletor constituído por um espelho esférico e um filamento de pequenas dimensões que pode emitir luz. O farol funciona bem quando o espelho é:
( )a) côncavo e o filamento está no centro do espelho;
( )b) côncavo e o filamento está no foco do espelho;
( )c) convexo e o filamento está no centro do espelho;
( )d) convexo e o filamento está no foco do espelho;
( )e) convexo e o filamento está no ponto médio entre o foco e o centro do espelho.
24. (UFES) – Um objeto está sobre o eixo de um espelho esférico côncavo. A distância entre o objeto e o espelho é maior que o raio de curvatura do espelho. A imagem do objeto é:
( )a) real, não invertida, menor que o objeto;
( )b) real, invertida, maior que o objeto;
( )c) real, invertida, menor que o objeto;
( )d) virtual, não invertida, maior que o objeto;
( )e) virtual, invertida, menor que o objeto.
25. (VUNESP) – Um pequeno prego se encontra diante de um espelho côncavo, perpendicularmente ao eixo óptico principal, entre o foco e o espelho. A imagem do prego será:
( )a) real, invertida e menor que o objeto;
( )b) virtual, invertida e menor que o objeto;
( )c) real, direta e menor que o objeto;
( )d) virtual, direta e maior que o objeto;
( )e) real, invertida e maior que o objeto.
26. (FUND. UNIV. DE ITAÚNA) Uma pessoa observou a sua imagem, formada na parte côncava de uma colher bem polida. Em relação à imagem formada, é CORRETO afirmar que:
( )a) a imagem formada nunca é invertida;
( )b) a imagem formada é sempre invertida;
( )c) quando não invertida, a imagem é real;
( )d) quando não invertida, a imagem é virtual;
( )e) a imagem formada é virtual e não invertida.
27. (MACKENZIE) – Diante de um espelho esférico côncavo coloca-se um objeto real no ponto médio do segmento definido pelo foco principal e pelo centro de curvatura. Se o raio de curvatura desse espelho é de $\color{Maroon}{R = 2,4\,m}$, a distância entre o objeto e sua imagem conjugada é de:
( )a) 0,60m;
( )b) 1,2m;
( )c) 1,8m;
( )d) 2,4m;
( )e) 3,6m.
28. (UCS) – Um espelho esférico conjuga a um objeto real, a $\color{Maroon}{p = 40\,cm}$ de seu vértice, uma imagem direita e duas vezes menor. Pode-se afirmar que o espelho é:
( )a) côncavo de 40 cm de distância focal;
( )b) côncavo de 40cm de raio de curvatura;
( )c) convexo de 40cm de módulo de distância focal;
( )d) convexo de 40cm de raio de curvatura;
( )e) convexo de 40cm como distância entre o objeto e a imagem.
29. (PUC – RJ) – Um objeto é colocado perpendicularmente ao eixo principal de um espelho esférico convexo. Notamos que, nesse caso, a altura de sua imagem é $\color{Maroon}{i_{1}}$. Em seguida, o mesmo objeto é aproximado do espelho, formando uma nova imagem, cuja altura é $\color{Maroon}{i_{2}}$ Quando aproximamos o objeto, a imagem:
( )a) se aproxima do espelho, sendo $\color{Maroon}{i_{1}\lt i_{2}};
( )b) se aproxima do espelho, sendo $\color{Maroon}{i_{1}\gt i_{2}}$;
( )c) se aproxima do espelho, sendo $\color{Maroon}{i_{1} = i_{2}}$; ( )d) se afasta do espelho, sendo $\color{Maroon}{i_{1}\gt i_{2}}$; ( )e) se afasta do espelho, sendo $\color{Maroon}{i_{1}\lt i{2}}$.
30. (ITA) – Um jovem estudante para fazer a barba mais eficientemente, resolve comprar um espelho esférico que aumente duas vezes a imagem do seu rosto quando ele se coloca a $\color{Maroon}{p = 50\,cm}$ dele. Que tipo de espelho ele deve usar e qual o raio de curvatura?
( )a) Convexo com $\color{Maroon}{r = 50\,cm}$;
( )b) Côncavo com $\color{Maroon}{r = 2,0\,m}$;
( )c) Côncavo com $\color{Maroon}{r = 33\,cm}$;
( )d) Convexo com $\color{Maroon}{r = 67\,cm}$;
( )e) Um espelho diferente dos mencionados.
Havendo dúvidas, disponha de minha orientação por meio de um dos canais citados abaixo.
Curitiba, 21 de setembro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
