Física – Mecânica – Cinemática
Movimento retilíneo uniformemente variado – MRUV
Parte II
Equação horária do MRUV
No post anterior falamos das grandezas velocidade e aceleração no MRUV. Agora é hora de relacionar estas grandezas com a posição do móvel sobre a trajetória.
Vimos que $\Delta{V} = {a}\times\Delta{t}$
E também $ V = V_{0} + a\times{t}$
Vejamos um móvel em trajetória reta, como representado abaixo.
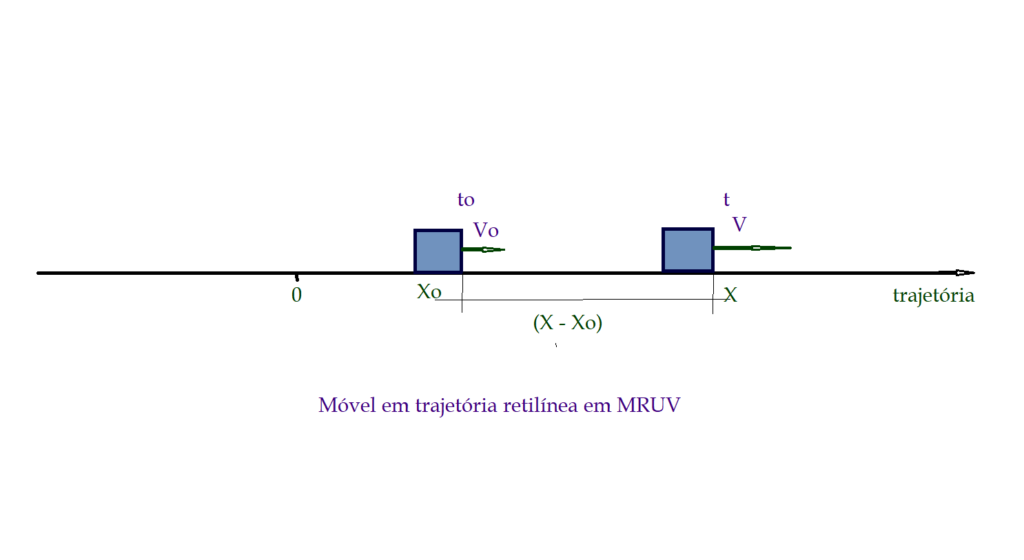
Se considerarmos uma velocidade média para o deslocamento ${\Delta{X} = {(X – X_0)}}$ existem duas possibilidades.
Podemos dividir o deslocamento ${\Delta{X}}$ pelo intervalo de tempo ${\Delta {t}}$, como se o movimento fosse uniforme nesse intervalo, ou podemos fazer a média aritmética das velocidades ${V_{0}}$ e ${V}$. Isso nos dá as seguintes expressões.
- $V_{m} = \left(\frac{\Delta{X}}{\Delta{t}}\right)$$\Leftrightarrow$$V_{m}=\left(\frac{X – X_{0}}{t – 0}\right)$
- $V_{m} = \left(\frac{V_{0} + V} {2,0}\right)$$\Leftrightarrow$$V_{m}=\left(\frac{V_{0} + V}{2,0}\right)$
- Tratando-se do mesmo movimento, as duas velocidades médias são iguais e portanto podemos igualar as duas expressões e desenvolver completamente.
- $\left(\frac{X – X_{0}}{t – 0}\right) = \left(\frac{V_{0} + V}{2,0}\right)$
- Se multiplicarmos os dois membros da igualdade pelo fator ${t}$ e substituirmos $V = V_{0} + a\times{t}$ no segundo membro, teremos:
- $\left(\frac{{X – X_{0}}\times{\not{t}}}{\not{t}}\right) = \frac{{(V_{0} + V_{0} + a\cdot t)}\times{t}}{2,0}$
- Vamos efetuar as operações possíveis. No primeiro membro simplificar o fator comum entre numerador e denominador. No segundo membro aplicar a propriedade distributiva da multiplicação em relação à adição/subtração.
- $ X – X_{0} = \frac{2\cdot V_{0}\times{t} + a\times t^{2}}{2,0}$
- $X – X_{0} = \frac{V_{0}\times{t} + {(V_{0} + a\times{t})\times{t}}}{2,0}$
- $X – X_{0} = \frac{V_{0}\times{t} + V_{0}\times{t} + a\times {t^{2}}}{2,0}$
- Reduzimos os termos semelhantes e separamos o segundo membro em duas frações, temos:
- $X – X_{0} = \frac{2,0\times V_{0}\times t}{2,0} + \frac{a\times t^{2}}{2,0}$
- $X = X_{0} + V_{0}\times{t} + \frac{a\times t^{2}}{2,0}$
- $X = X_{0} + V_{0}\times{t} + \frac{1,0}{2,0}\times{a\times{t^{2}}}$
Aí temos a equação horária da posição ${X}$ de um móvel em trajetória reta com aceleração constante. Se olharmos as funções da matemática, veremos que estamos diante de uma função do segundo grau ou seja uma função quadrática.
Comparando os dois casos:
$X = X_{0} + V_{0}\times{t} + \frac{1}{2}\times{at^{2}}$
$y = c + b\times{x} + a\times{x^{2}}$
Os termos que ocupam as mesmas posições se equivalem no momento da representação gráfica no plano cartesiano. ${X}$ corresponde ao ${y}$, $X_{0}$ corresponde ao ${c}$, $V_{0}$ corresponde ao ${b}$ e $\left(\frac{1}{2}\right)\times a$ equivale ao ${a}$ na expressão genérica.
Temos agora o conjunto das equações que nos permitem resolver os problemas relativos aos movimentos uniformemente variados em uma trajetória retilínea. Estas equações são atribuídas à Galileu Galilei que em suas pesquisas chegou a estas conclusões.
Para completar mesmo, vejamos o que um outro físico italiano fez, usando as equações obtidas pelo conterrâneo Galileu. Devemos à Evangelista Torricelli, entre outras invenções, uma combinação das equações vistas, onde não é necessário o fator tempo.
$V = V_{0} + a\times{t}$$\Leftrightarrow$$\left(\frac{V – V_{0}}{a}\right) = {t} $
$X – X_{0} = V_{0}\times{t} + \left(\frac{a}{2}\right)\times{t^{2}}$
Substituindo ${t}$ na segunda expressão, pelo valor obtido na primeira teremos:
$\Delta{X} = V_{0}\times\left(\frac{V – V_{0}}{a}\right) + \left(\frac{a}{2}\right)\times\left(\frac{V – V_{0}}{a}\right)^{2}$
Efetuando as operações indicadas.
$\Delta{X} = \left(\frac{{V}\times{V_{0}} – {V_{0}^{2}}{a}\right) + \left({a}\times(\frac{V^{2} – 2\times{V}\times{V_{0}} + {V_{0}^{2}}){2a^{2}}\right)$
Reduzindo ao mesmo denominador e cancelando os termos semelhantes.
${\Delta{X}\times{2a} = ({{V}\times{V_0} – {V_0}^2})\times {2} +({V^2 – 2\times{V}\times{V_0} + {V_0}^2})}$
${{2}\times{a}\times{\Delta{X}} = {2}\times{V}\times{V_0} – {2}\times{V_0}^2 + {V^2} – 2\times{V}\times{V_0} + {V_0}^2}$
${2a\Delta{X} = 2VV_0 – 2{V_0}^2 + V^2 – 2VV_0 +{V_0}^2}$
${2a\Delta{X} = – {V_0}^2 + V^2}$
$V^{2} = {V_{0}}^{2} + 2\times a\times\Delta{X}$
Esta é conhecida nos meios ligados à física como Equação de Torricelli. Ela é um excelente atalho para muitos problemas, pois encurta o caminho para chegar ao resultado que se deseja.
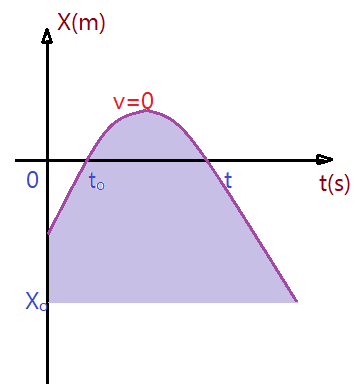
Ao estudar a representação gráfica das funções matemáticas, vemos que uma função do segundo grau resulta num gráfico em forma de parábola. A forma é aproximadamente assim.
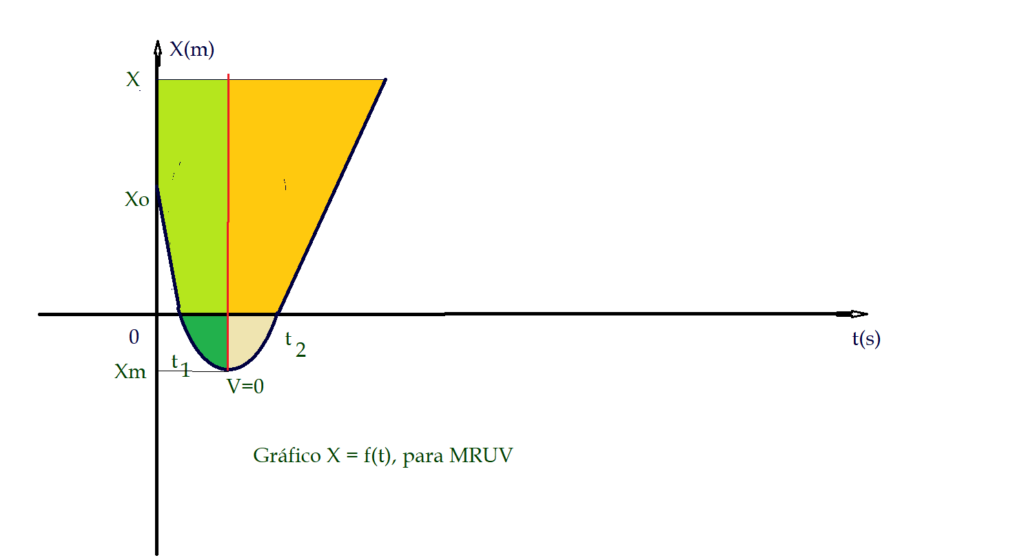
A parábola tem a concavidade para cima. Seu ponto inicial para ${t = 0}$, corresponde a uma curva descendente, ou seja um movimento retrógrado e retardado. No ponto mais baixo (${X_{mínimo}}$). a velocidade se anula e o sentido do movimento inverte, passando a ser progressivo e acelerado.
Sempre é bom fazer exercícios, onde se aplica o que foi visto na explanação teórica. Vejamos então.
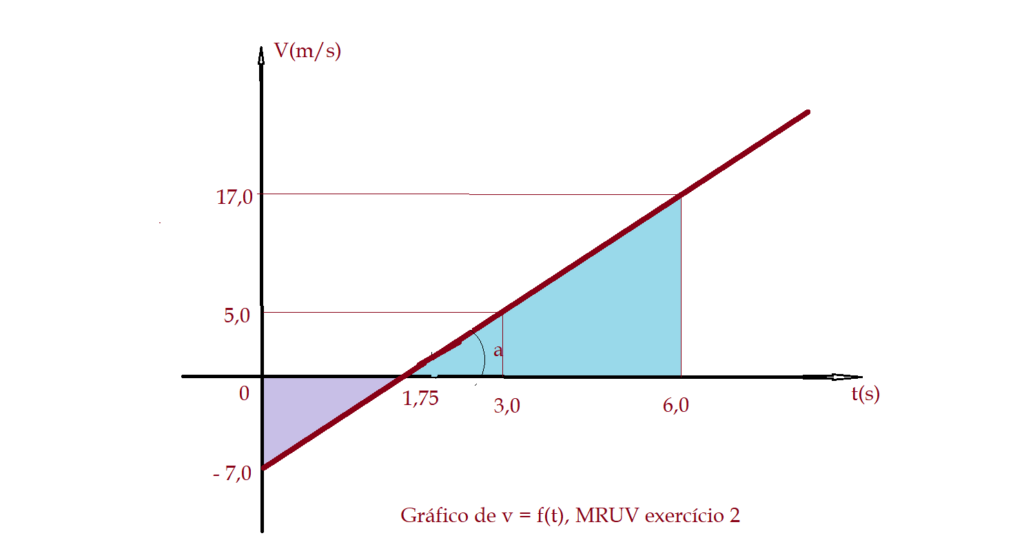
Um móvel se encontra na posição $X_{0}= – 12,0\,m$ no instante $t_{0} = 0$, com velocidade $V_{0} = 3,0\, m/s$ e sua aceleração é $ a = 2,0\,\,m/s^2$. Pede-se: a) escreva a equação horária da velocidade; b) escreva a equação horária da posição do móvel; c) determine a posição do mesmo no instante $t = 5,0\,s$; d) qual foi o deslocamento realizado até o instante em que a velocidade é $V= 17,0\,\,m/s$.
- a) temos que $V = V_{0} + a\times{t}$
- $V_{0} = 3,0\,m/s$
- $a = 2,0\, m/s^2$
- Substituindo na equação fica: $V = 3,0 + 2,0 \times {t}$
- b) temos que $X = X_{0} + V_{0}\times{t} + \frac{1}{2}\times{a}\times{t^2}$
- $X_{0} = -12,0\,m$
- $a = 2,0\, m/s^2$
- $V_{0} = 3,0\,m/s$
- substituindo na equação temos:
- $X = -12,0 + {3,0}\times{t} + \frac{1}{2}\times{2,0}\times{t^2}$
- c) $t = 5,0 s$
- $X = {-12,0} + {3,0}\cdot{5,0} + \frac{1}{2}\times{2,0}\times{5,0}^2$
- $X = -12,0 + 15,0 + \frac{1}{2}\times{50}$
- $X = 3,0 + 25,0$$\Leftrightarrow$$X = 28,0\,m$
- d) para resolver essa questão podemos fazer uso da Equação de Torricelli.
- $V^{2} = v_{0}^{2} + 2\times{a}\times{\Delta{X}}$
- $V = 17,0\,m/s$
- ${17,0}^{2} = {3,0}^{2} + 2\times{2,0}\times {\Delta{X}}$
- $289,0 = 9,0 + {4,0}\times\Delta{X}$
- ${289,0 – 9,0} = {4,0}\times\Delta{X}$
- $\frac{280,0}{4,0} = \Delta{X}$
- $\Delta{x} = 70,0\, m$
Um móvel parte de uma posição inicial $X_{0} = 25,0\,m$ com uma velocidade $V_{0} = -7,0\, m/s $. Se após $t = 3,0\, s$ ele se encontra com velocidade $V = 5,0\,m/s$, pergunta-se:
- a)qual é a sua aceleração?
- temos que ${{V_0} = -7,0\,\,m/s}$
- ${ t = 3,0\,\,s}$
- ${V = 5,0\,\,m/s}$
- ${ V = {V_0} + a\times{t}}$
- substituímos ${ 5,0 = – 7,0 + a\times{3,0}}$
- ${{5,0 + 7,0} = a\cdot {3,0}}$$\Leftrightarrow$${a = {\frac{12,0}{3,0}}}$
- ${a = 4,0\,\,m/s^2}$
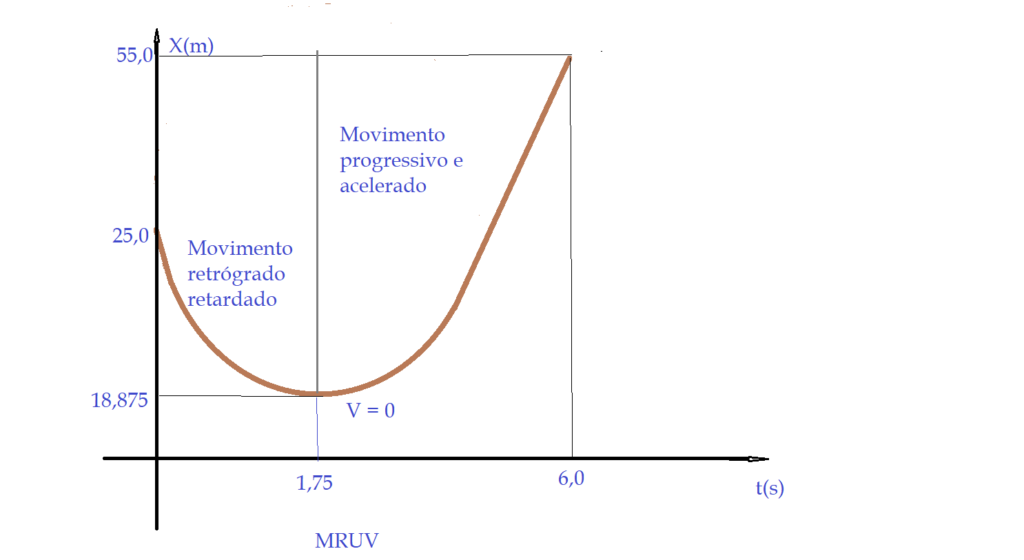
- b) qual é a posição do móvel no instante ${t = 6,0 s}$?
- ${X = {X_0} + {V_0}\times {t} + {\frac{1}{2}}\times{a}\times{t^2}}$
- ${X = 25,0 + {- 7,0}\times {6,0} + {\frac{1}{2}}\times{4,0}\times {6,0}^2}$
- $X = 25,0 – 42,0 + 2,0\times{36,0}$
- $X = -17,0 + 72$$\Leftrightarrow$$X = 55,0\,m$
- c)Em que posição o móvel se encontra no momento da inversão de velocidade? (passa a ser acelerado).
- $V = 0$$\Rightarrow$ no instante da inversão da velocidade.
- $V^2 = V_{0}^{2} + 2\times{a}\times\Delta {X}$
- $\Delta{X} = X – X_{0}$
- $ 0 = {-7,0}^{2} + 2\times{4,0}\times{X -X_{0}}$
- $0 = 49,0 + {8,0}\times{X – {25,0}}$$\Leftrightarrow$$0 = 49,0 + {8,0}X – 200,0$
- ${-8,0}X = -151,0$$\Leftrightarrow$$x = \frac{-151,0}{-8,0}$
- $X = {18,875\,m}$
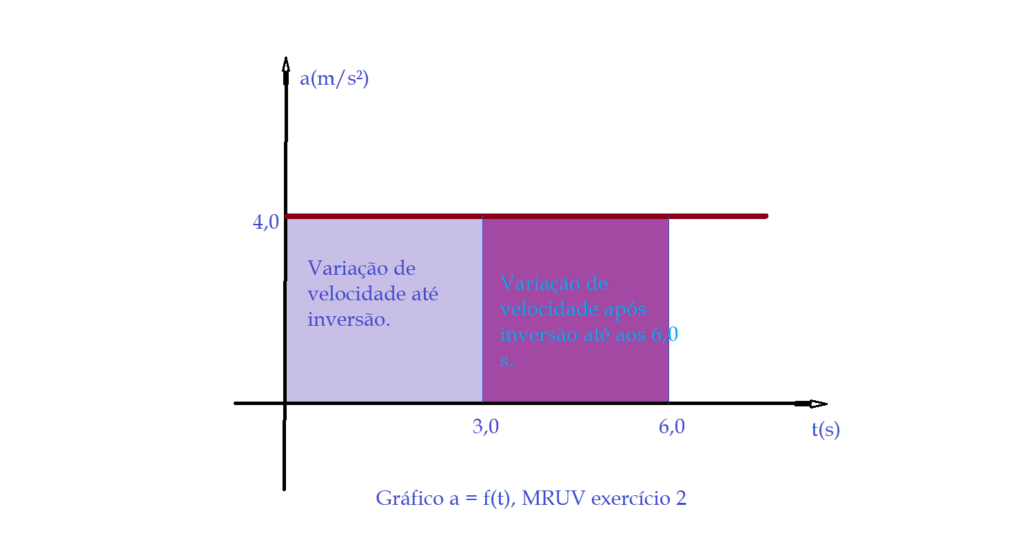
- d) Construa os gráficos $X = f(t)$, $v = f(t)$ e $a = f(t)$
Alguns exercícios para treinar.
- Um móvel parte da origem dos eixos ortogonais X =f(t), com velocidade igual a zero. Se aos $12,0\,s$ do movimento sua velocidade é de $36\,m/s$, determine: a) a aceleração; b) a posição nesse instante; c) o momento em que sua velocidade e igual $v = 27,0\,m/s$; d) faça os gráficos $X =f(t)$, $V =f(t)$ e $a = f(t)$.
- Se um corpo parte da posição $X_{0} = – 35,0\,m$, com velocidade $V_{0} = 7,0\, m/s $, sendo acelerado de $a = 2,0\,m/s^{2}$. pede-se: a) em que instante ele irá passar na origem da trajetória; b) com que velocidade ele estará nesse momento; c) depois de quanto tempo ele passará na posição $X = 35,0\,m$; d) construa o gráfico $X = f(t)$ e analise-o; e)construa os gráficos $V = f(t)$ e $a = f(t)$ e analise.
- Qual é o deslocamento de um móvel que tem $V_{0} = 8,0\,m/s$, aceleração $a= 3,0\,m/s^{2}$ até atingir a velocidade $V = 38,0\,m/s$?
- Um móvel que percorre uma distância $\Delta{X} = 48,0\,m$, num intervalo de tempo $\Delta{t} = 6,0\,s$, com movimento acelerado a partir do repouso, tem qual aceleração? Se sua posição inicial é $X_{0} = -12,0\,m$, qual é sua posição no instante $t = 6,0\,s$?
5. Determine a velocidade inicial $v_{o}$, o espaço inicial $x_{o}$ e a aceleração do móvel $a$ uma vez que o mesmo encontra-se em MRUV seguindo a função $S=20-2\times t + t^{2}$, Grandezas medidas no SI.
6. Um determinado veiculo em certo instante, possui uma velocidade de $V_{o}=20\,m/s$. A partir deste instante o condutor do veiculo acelera seu carro constantemente em $a = 4,0\,m/s^{2}$. Qual a velocidade que o automóvel terá após ter percorrido $\Delta X = 130,0\,m$.
7. (UFPR) Em uma prova internacional de ciclismo, dois dos ciclista, um francês e, separado por uma distância de $\Delta X=15\,m$ à sua frente, um inglês, se movimentam com velocidades iguais e constantes de módulo $v=22\, m/s$.
Considere agora que o representante brasileiro na prova, ao ultrapassar o ciclista francês, possui uma velocidade constante de módulo $v_{b}=24\, m/s$ e inicia uma aceleração constante de módulo $a=0,4\,m/s^{2}$ com o objetivo de ultrapassar o ciclista inglês e ganhar a prova. No instante em que ele ultrapassa o ciclista francês, faltam ainda $|Delta X_{f}=200\,m$ para a linha de chegada.
Com base nesses dados e admitindo que o ciclista inglês, ao ser ultrapassado pelo brasileiro, mantenha constantes as características do seu movimento, assinale a alternativa correta para o tempo gasto pelo ciclista brasileiro para ultrapassar o ciclista inglês e ganhar a corrida.
a) 1 s;
b) 2 s;
c) 3 s;
d) 4 s;
e) 5 s.
8. (IFBA) O Beach park, localizado em Fortaleza – CE, é o maior parque aquático da América Latina situado na beira do mar. Uma das suas principais atrações é um toboágua chamado “Insano”. Descendo esse toboágua, uma pessoa atinge sua parte mais baixa com velocidade módulo $v=28\,m/s$. Considerando-se a aceleração da gravidade com módulo $g= 10\,m/s^{2}$ e desprezando-se os atritos, estima-se que a altura do toboágua, em metros, é de:
a) 28;
b) 274,4;
c) 40;
d) 2,86;
e) 32.
9. Um móvel tem a sua função horária de deslocamento dada por $S = 5 + t^{2}$. Assinale a alternativa que indica a velocidade inicial e a aceleração desse móvel, respectivamente:
a) 5 m/s e 1 m/s^{2};
b) 0 m/s e 2 m/s^{2};
c) 1 m/s e 5 m/s^{2};
d) 5 m/s e 2 m/s^{2};
e) 3 m/s e 5 m/s^{2}.
10. Em um gráfico de posição em função do tempo, observa-se que a curva descreve uma parábola com a sua concavidade voltada para baixo. Em relação a esse gráfico, assinale a alternativa correta:
a) Trata-se de um movimento acelerado;
b) Trata-se do gráfico de um movimento retrógrado;
c) Trata-se do gráfico de um movimento retardado;
d) Trata-se de um gráfico de aceleração variável;
e) Trata-se de um gráfico de velocidade crescente.
11. (UFPA) Um ponto material parte do repouso em movimento uniformemente variado e, após percorrer 12 m, está animado de uma velocidade escalar de 6,0 m/s. A aceleração escalar do ponto material, em m/s, vale:
a) 1,5;
b) 1,0;
c) 2,5;
d) 2,0;
e) N.d.a.
12. Um móvel parte do repouso e percorre uma distância de $\Delta X =200\, m$ em $t=20\,s$. A aceleração desse móvel, em m/s^{2}, é:
a) 0,5;
b) 0,75;
c) 1;
d) 1,5;
e) 2.
13. Uma pedra é lançada para baixo, do décimo andar de um prédio com velocidade inicial de $v_{o}=5\,m/s$. Sendo a altura nesse ponto igual a $h=30\,m$ e a aceleração da gravidade igual a $g=10\,m/s^{2}$ a velocidade da pedra ao atingir o chão é:
a) 5 m/s;
b) 25 m/s;
c) 50 m/s;
d) 30 m/s;
e) 10 m/s.
14. (Enem 2013 – edição PPL) – O trem de passageiros da Estrada de Ferro VitóriaMinas (EFVM), que circula diariamente entre a cidade de Cariacica, na Grande Vitória, e a capital mineira Belo Horizonte, está utilizando uma nova tecnologia de frenagem eletrônica. Com a tecnologia anterior, era preciso iniciar a frenagem cerca de $\Delta X_{1}=400\, m$ antes da estação. Atualmente, essa distância caiu para $\Delta X_{2}=250\,m$, o que proporciona redução no tempo de viagem. Considerando uma velocidade de $v_=72\, km/h$, qual o módulo da diferença entre as acelerações de frenagem depois e antes da adoção dessa tecnologia?
a) 0,08 m/s^{2};
b) 0,30 m/s^{2};
c) 1,10 m/s^{2};
d) 1,60 m/s^{2};
e) 3,90 m/s^{2}.
Havendo dúvidas, seja com esses exercícios propostos ou outros que tenha obtido de outra origem, não hesite em perguntar. Para isso servem os canais de comunicação que coloco abaixo.
Curitiba, 15 de setembro de 2019
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732