FI.ME.013-02- Física – Mecânica, estática. Momento resultante, Teorema de Varignon.
Aplicações do Teorema de Varignon.
Vamos ver como podemos usar o Teorema de Varignon, na solução de vários problemas de estática. Esse assunto é especialmente útil na solução de problemas relativos a construção de estruturas de engenharia, na distribuição de cargas sobre os apoios, vigas e colunas. Não iremos tratar a fundo do assunto, pois isso cabe aos engenheiros, levando em conta algumas particularidades ainda fora do nosso alcance. Mas podemos ter uma pequena ideia de como funciona essa questão.
- Seja uma viga uniforme, de peso $\color{Navy}{P = 50000\,N}$, apoiada sobre dois apoios $\color{Navy}{A}$ e $\color{Navy}{B}$, conforme mostra a figura abaixo. Sobre ela temos apoiados dois corpos nas posições indicadas. Determinar a intensidade das reações de apoio em $\color{Navy}{R_{A}}$ e $\color{Navy}{R_{B}}$.
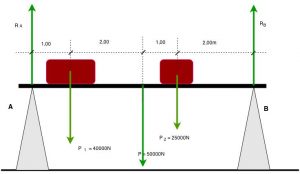
Observando o sistema de forças presente no sistema, notamos que todas elas são verticais (mesma direção), sendo algumas dirigidas para baixo e outras para cima. Como a viga está em equilíbrio, temos que o sistema de forças tem resultante igual a zero. Vamos aplicar esse conceito.
- $\color{Navy}{{R_{A}} + {R_{B}} – {P} – {P_{1}} – {P_{2}} = 0}$
- $\color{Navy}{{R_{A}} + {R_{B}} – 50000 – 40000 – 25000 = 0}$
- $\color{Navy}{{R_{A}} + {R_{B}} – 115000 = 0}$
- $\color{Navy}{{R_{A}} + {R_{B}} = 115000}$
- A soma das reações dos apoios A e B sobre a viga, é igual a soma dos pesos da viga e dos corpos apoiados sobre ela. Como conseguiremos saber qual o valor de cada uma das reações?
Temos um outro recurso de cálculo, que é o Teorema de Varignon. Vamos lembrar?
“O momento da resultante de um sistema de forças em relação a um ponto é igual a soma dos momentos das forças componentes em relação ao mesmo ponto”.
Vamos escolher um ponto qualquer como referência. Para facilidade de raciocínio, vamos adotar o ponto A. Como a resultante é nula, também o momento resultante é nulo. As forças peso tem em relação ao ponto A sentido horário e a reação no ponto B tem sentido anti-horário. Já a reação em A, também terá momento nulo, pois é aplicada no próprio ponto de rotação. Portanto teremos:
- $\color{Navy}{\overline{M_{A}F_{R}} = \overline{R_{A}}\cdot 0 + \overline{R_{B}}\cdot 6,0 + \overline{P_{1}}\cdot 1,0 +\bar{P}\cdot 3,0 +\overline{P_{2}}\cdot 4,0}$
- $\color{Navy}{{ 0\cdot x} = {0} + \overline{R_{B}}\cdot 6,0 +{-40000\cdot 1,0} +{-50000\cdot 3,0} + {-25000\cdot 4,00}}$
- $\color{Navy}{{0} = \overline{R_{B}}\cdot 6,0 +{- 40000 – 150000 – 100000}}$
- $\color{Navy}{{R_{B}}\cdot 6,0 – {310000} = 0}$
- $\color{Navy}{{R_{B}} = {290000\over 6,0} = {48.333,33\,N}}$
- $\color{Navy}{{R_{B}} = 48.333,33\,N}$
Como vimos acima.
- $\color{Navy}{\overline{R_{A}} + \overline{R_{B}} = 115000\,N}$
Vamos substituir e determinar a reação em $\color{Navy}{R_{A}}$.
- $\color{Navy}{\overline{R_{A}} + 48333,33 = 115000}$
- $\color{Navy}{{R_{A}} =115000 – 48333,33}$
- $\color{Navy}{{R_{A}} = 66.666,67\,N}$
Note que o apoio A suporta mais peso que o B, pois a carga maior está deslocada para o lado dela. Se a viga não fosse uniforme, o cálculo seria mais complexo, envolvendo métodos mais sofisticados do que esses que empregamos aqui. Vamos colocar isso em prática para os exercícios abaixo.
- Determine as intensidades das reações de apoio nos pontos 1 e 2 da figura.
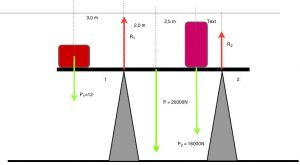
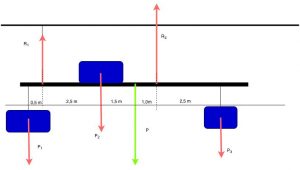
- Nesse caso os apoios são substituídos por dois tirantes (1) e (2). Determine as trações existentes nesses tirantes.
Em caso de dúvidas, não hesite em contatar comigo por um dos canais abaixo. Estou às suas ordens para tirar qualquer dúvida.
Curitiba, 27 de abril de 2015 (Revisado e atualizado em 05/08/2016)
Décio Adams
www.facebook.com/livros.decioadams
www.facebook.com/decioadams.matfisonline
Telefone: (41) 3019-4760
Celular e WhatsApp: (41) 99805-0732
